Meson octets/nonets (Gell-Man’s Eightfold Way), baryon octets & decuplets by plotting strangeness vs. isospin.
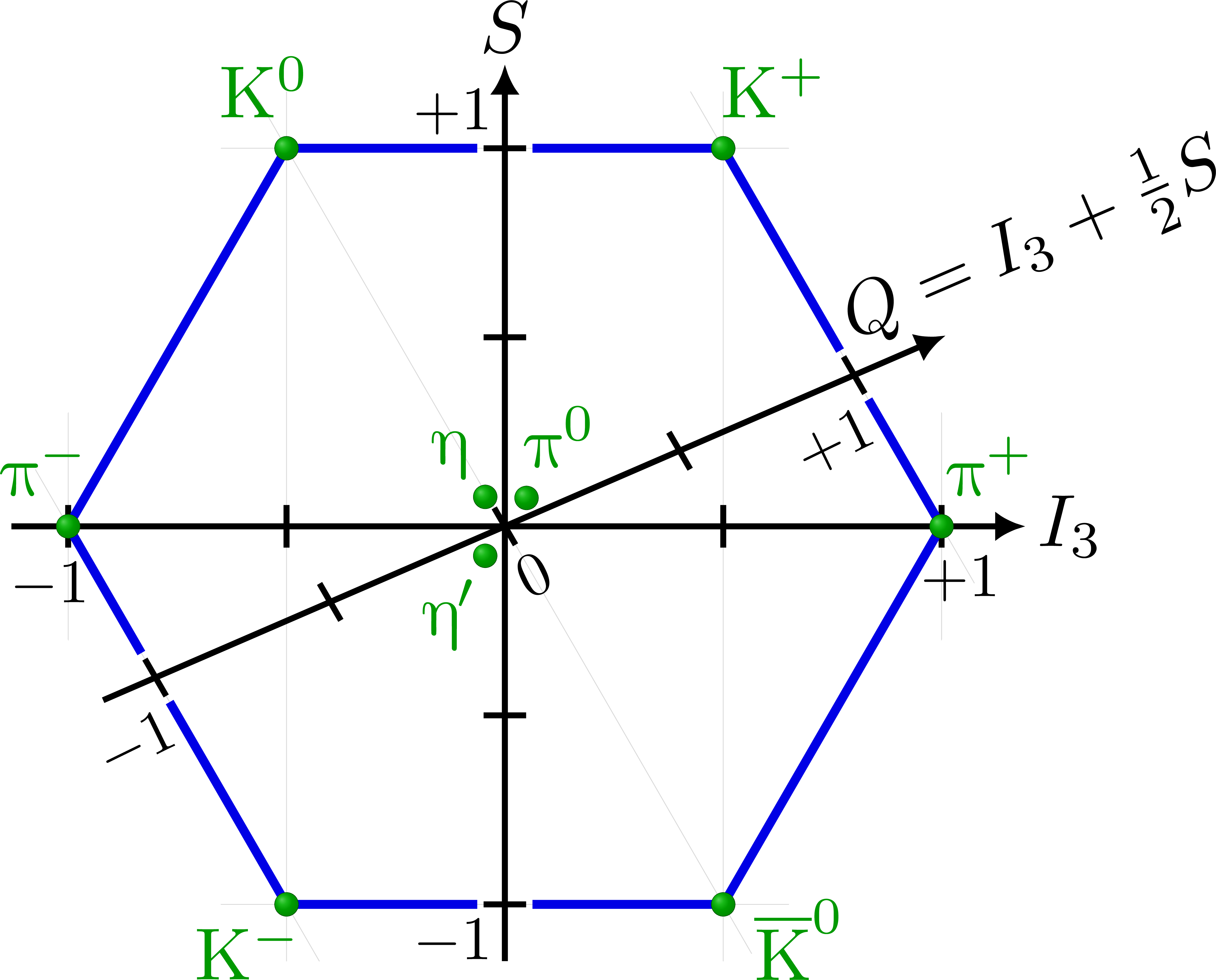
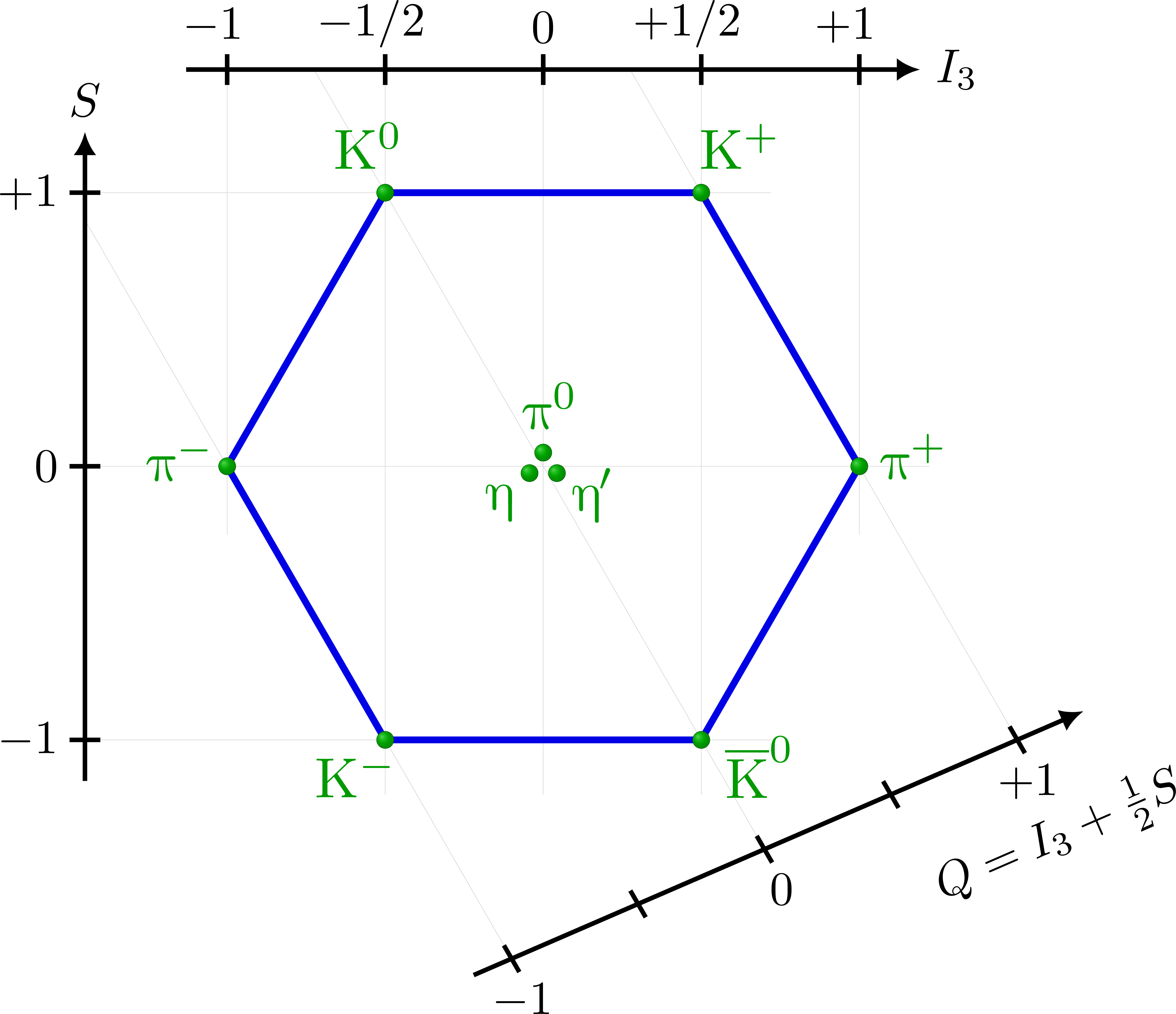
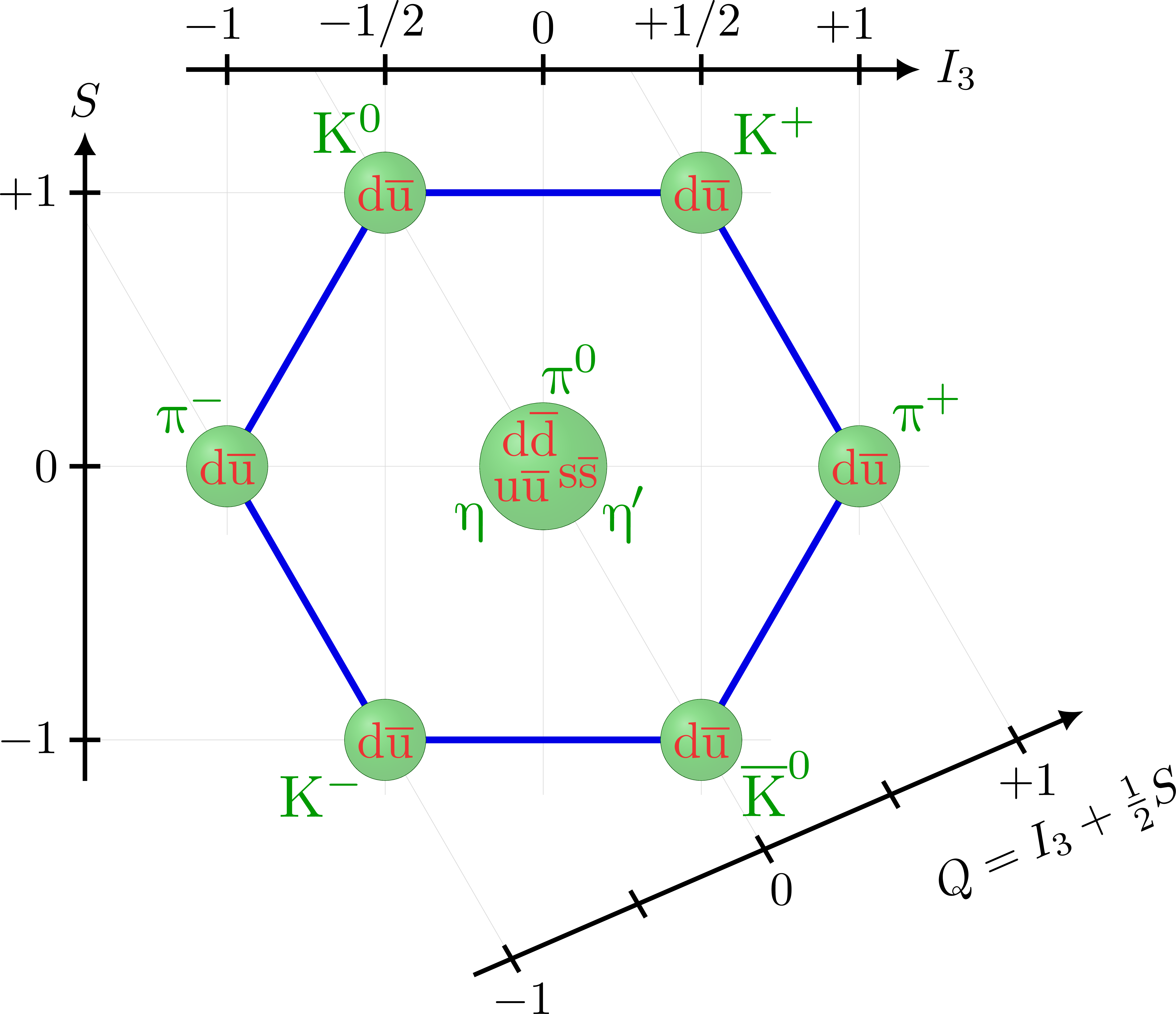
Pseudoscalar meson nonet
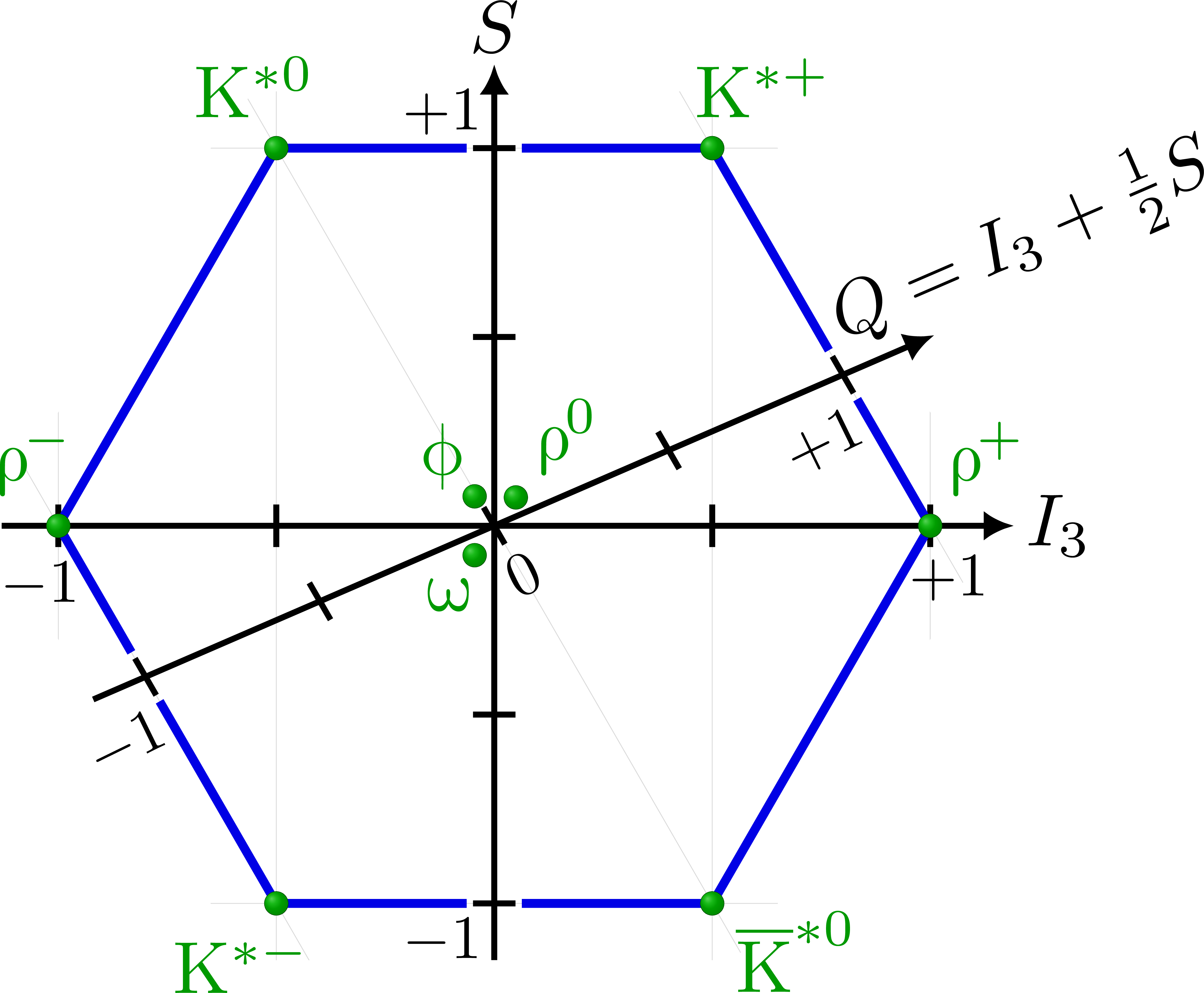
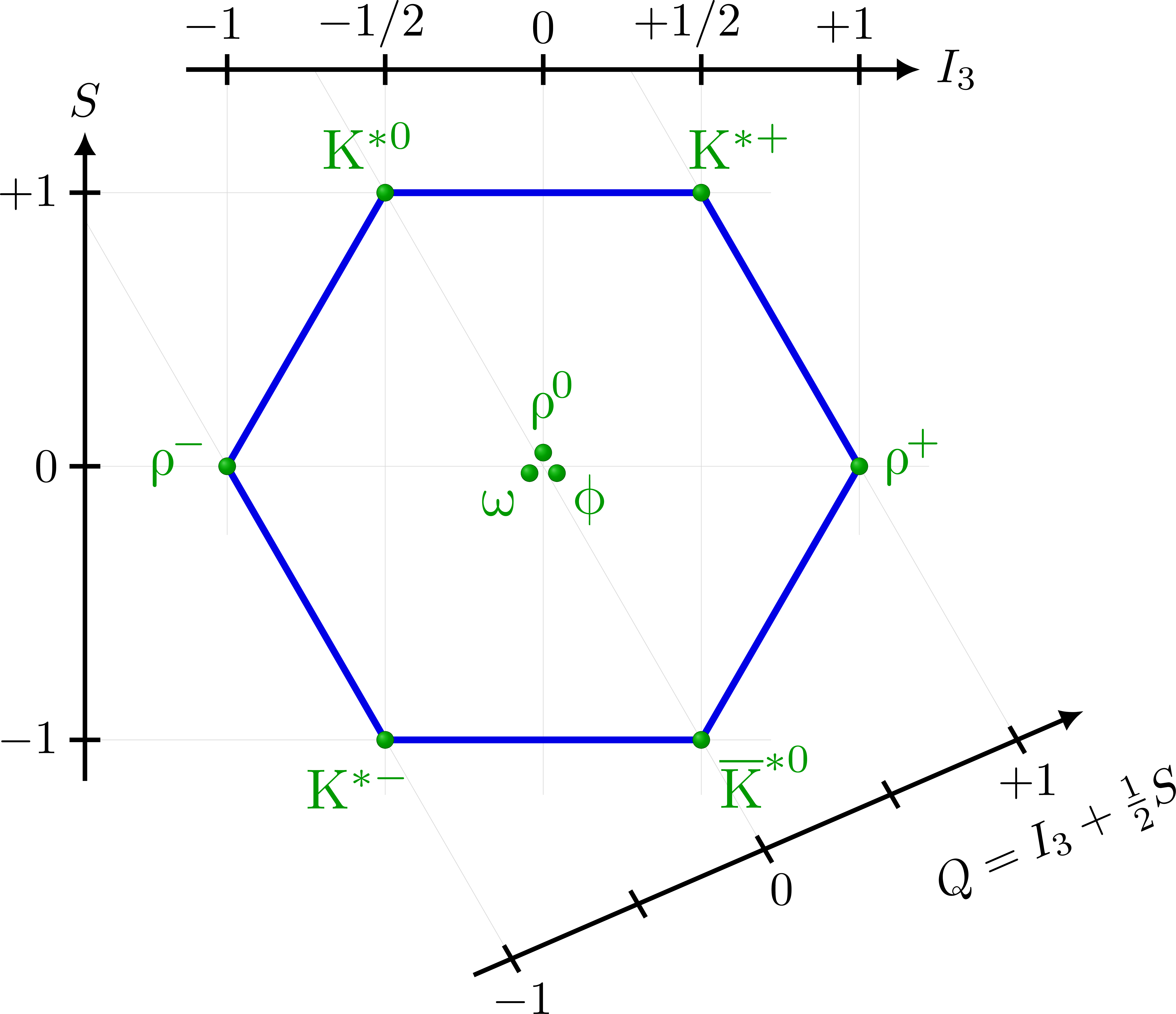
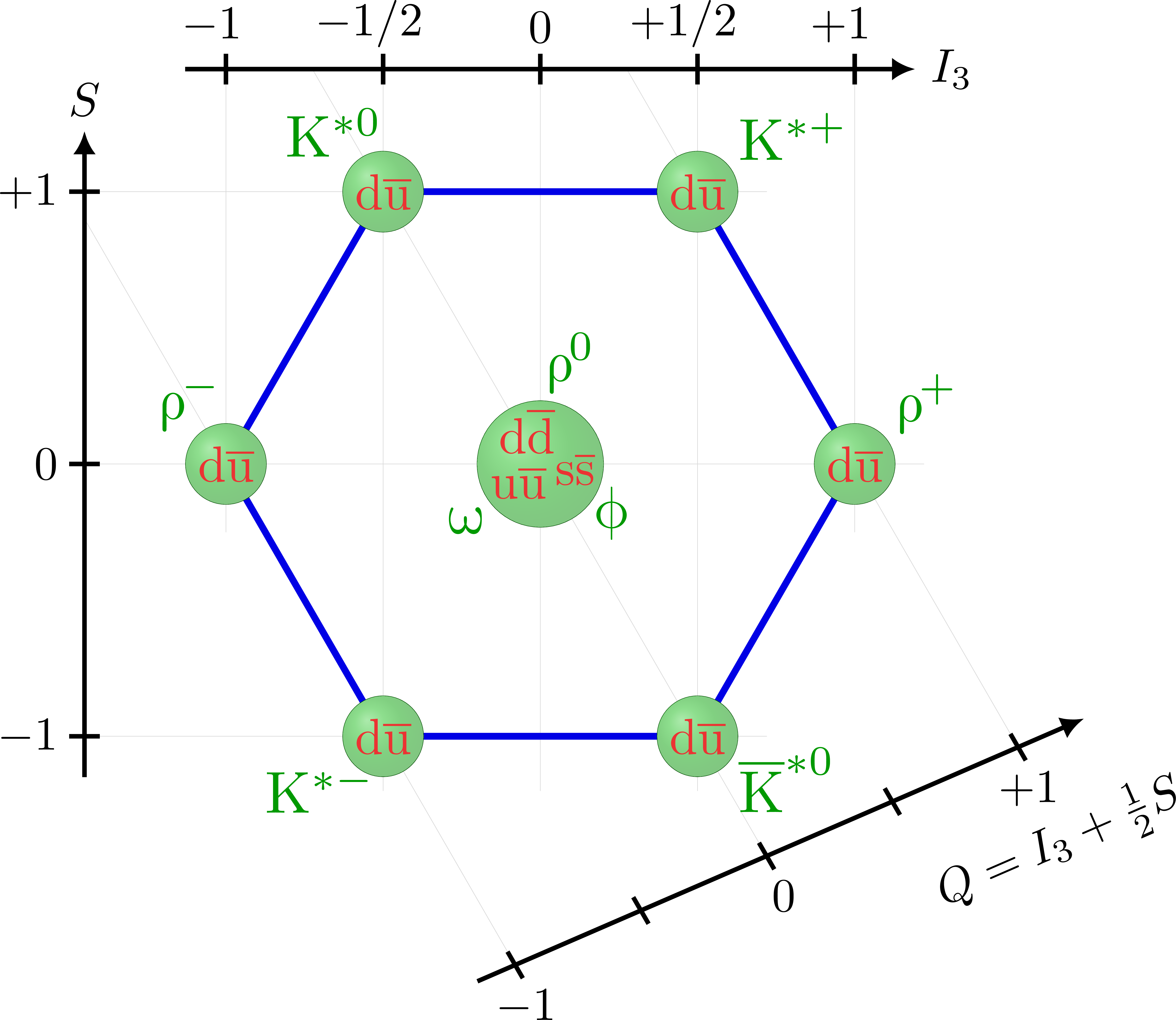
Vector meson nonet
Baryon octet
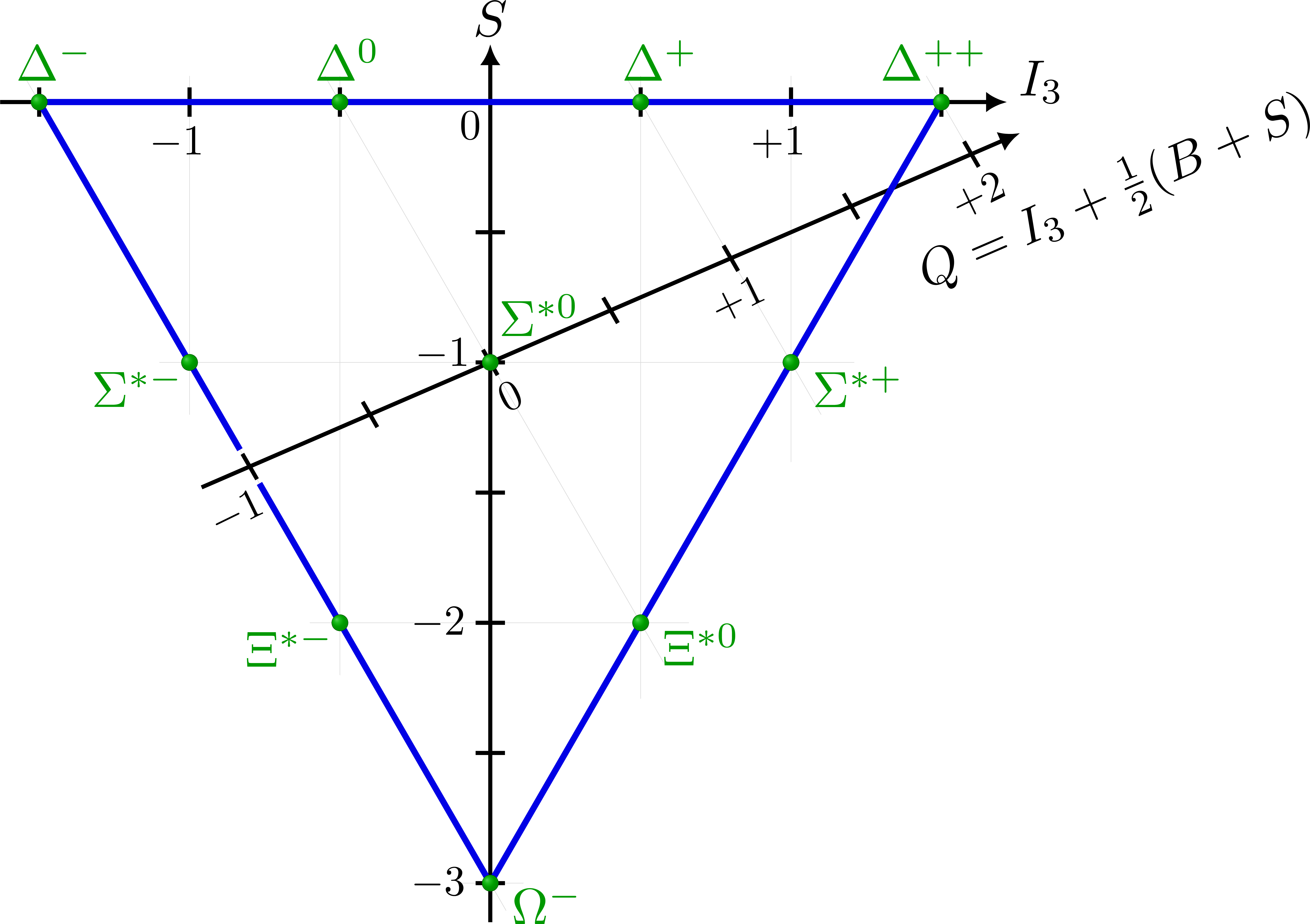
Baryon decuplet
Edit and compile if you like:
% Author: Izaak Neutelings (July 2023)
% Description:
% Meson & baryon octets/nonets and decuplets with I3-S-Q axes
% Sources:
% https://en.wikipedia.org/wiki/Gell-Mann–Nishijima_formula
% https://en.wikipedia.org/wiki/Quark_model
% https://en.wikipedia.org/wiki/Eightfold_way_(physics)
% https://commons.wikimedia.org/wiki/File:Meson-octet-small.svg
% https://commons.wikimedia.org/wiki/File:Baryon-octet-small.svg
% https://commons.wikimedia.org/wiki/File:Baryon-decuplet-small.svg
\documentclass[border=3pt,tikz]{standalone}
\usepackage{amsmath} % for \text
\usetikzlibrary{arrows.meta} % to control arrow size
\tikzset{>={Latex[length=4,width=4]}} % for LaTeX arrow head
\usetikzlibrary{calc}
\usepackage{xcolor} % for colored text
% COLORS
\colorlet{myblue}{blue!90!black}
\colorlet{mydarkblue}{blue!40!black}
\colorlet{myred}{red!90!black!80}
\colorlet{mygreen}{green!60!black}
\colorlet{mylightgreen}{green!75!black}
% STYLES
\renewcommand\bar[1]{\overline{\mathrm{#1}}}
\newcommand\PM[2]{$\mathrm{#1\overline{#2}}$} % meson
\tikzset{
guide/.style={ultra thin,black!15,line cap=round},
myball/.style={line width=0.05,ball color=#1},
tick/.style={scale=0.84,inner sep=1pt},
pname/.style={mygreen,scale=1.05,inner sep=0pt,outer sep=#1pt}, % particle name
lineheight/.style={execute at begin node=\setlength{\baselineskip}{#1}},
particle/.style={
circle,scale=0.9,minimum size=#1,inner sep=0.5pt,outer sep=1pt, %font=\bf,
myred,ball color=mygreen,align=center,lineheight=6pt,
postaction={fill=green!77!black!37,fill opacity=0.8,
draw=mygreen!50!black,line width=0.05}
},
pname/.default=0
}
% UNSLANT GREEK LETTERS for particle symbols
% https://tex.stackexchange.com/questions/145926/upright-greek-font-fitting-to-computer-modern
% https://tex.stackexchange.com/questions/236915/adjust-custom-made-upright-greek-letters-when-used-in-subscripts
\usepackage{scalerel}
\newsavebox{\foobox}
\newcommand{\slantbox}[2][0]{\mbox{%
\sbox{\foobox}{#2}%
\hskip\wd\foobox
\pdfsave
\pdfsetmatrix{1 0 #1 1}%
\llap{\usebox{\foobox}}%
\pdfrestore
}}
\newcommand\unslant[2][-.25]{%
%\mkern1.2mu%
\ThisStyle{\slantbox[#1]{$\SavedStyle#2$}}%
\mkern-2.2mu%
}
\newcommand{\PGe}{\unslant\eta}
\newcommand{\PGp}{\unslant\pi}
\newcommand{\PGr}{\unslant\rho}
\newcommand{\PGf}{\unslant\phi}
\newcommand{\PGo}{\unslant\omega}
% SETTINGS: (default) lengths, angles, scale factors, ...
\def\r{0.9pt} % point radius
\def\Lgrid{1.45} % maximum length of grid lines
\def\ltick{1.6pt} % tick length
%\pgfmathsetmacro\xs{2/sqrt(3)} % unit I3 isospin to make octagon with equal sides (2/tan(60))
\def\lmask{1.3*\ltick} % extend tick length to mask line
\def\lqmask{1.3*\lqtick} % extend tick length to mask line
\def\NtickS{2} % number of ticks along S axis
\def\Smin{-1} % S axis minimum
\def\Smax{ 1} % S axis maximum
\def\Qmin{-1} % Q axis minimum
\def\Qmax{ 1} % Q axis maximum
\def\Imin{-1} % I3 axis minimum
\def\Imax{ 1} % I3 axis maximum
\def\Qoffset{-1.75} % offset of X axis
\def\computeParameters{ % compute common parameters (angles, scales, ...)
\pgfmathsetmacro\ang{atan(0.5)} % angle between I3 and Q axes
\pgfmathsetmacro\angs{atan(\xs/2)} % angle between I3 and Q axes (x scaled) for lines
\pgfmathsetmacro\angt{atan(0.5/\xs)} % angle Q axis title
\pgfmathsetmacro\angl{.4*\angs+.6*\angt} % angle Q tick label
\pgfmathsetmacro\qs{cos(\ang)} % unit Q charge in (I3,S)
\pgfmathsetmacro\qss{\xs*cos(\angs)} % unit Q charge in (I3,S)
\pgfmathsetmacro\ts{\xs/sqrt(\xs^2*cos(\ang)^2+sin(\ang)^2)} % scale tick on Q axis
\def\lqtick{\ts*\ltick} % tick length on Q axis (x scaled)
\message{^^J- xscale xs = \xs}
\message{^^J- angle ang = \ang}
\message{^^J- angle angs = \angs (x-scaled)}
\message{^^J- angle angt = \angt (for title)}
\message{^^J- charge unit qs = \qs}
\message{^^J- charge unit qss = \qss (x-scaled)}
}
% COMMON MACROS
\def\tick#1#2{\draw[thick] (#1) ++ (#2:\ltick) --++ (#2-180:2*\ltick)}
\def\qtick#1{ % ticks on the Q axis
\draw[thick] % parallel to grid lines
(\ang:\qs*#1) ++ (90+\angs:\ltick) --++ (\angs-90:2*\ltick)
%\draw[thick] % perpendicular to Q axis
% (\ang:\qs*#1) ++ (90+\ang:{\lqtick/\xs} and {\lqtick})
% --++ (\ang-90:{2*\lqtick/\xs} and {2*\lqtick})
}
\def\particle(#1){ % small ball
\fill[mygreen,ball color=mygreen,postaction={
fill=mylightgreen,fill opacity=0.6,draw=mygreen!50!black,line width=0.04}]
(#1) circle(\r)
}
\def\mesonNode(#1){\node[particle=16pt] (P) at (#1)}
\def\baryonNode(#1){\node[particle=20pt] (P) at (#1)}
% MACROS for GRIDS
\def\drawGrid#1{ % GRID for mesons
\begin{scope}[shift={(0,#1)}] % vertical shift
\clip[scale=1.15,rounded corners=4pt] % octagon
(1,0) -- (1/2,1) -- (-1/2,1) -- (-1,0)
-- (-1/2,-1) -- (1/2,-1) -- cycle;
\foreach \i in {1,2}{
\draw[guide] (-\i/2,-\Lgrid) -- (-\i/2,\Lgrid); % isospin I3
\draw[guide] ( \i/2,-\Lgrid) -- ( \i/2,\Lgrid); % isospin I3
}
\foreach \i in {-1,0,1}{
\draw[guide] (-\Lgrid,\i) -- (\Lgrid,\i); % strangeness S, hypercharge Y
}
\foreach \i [evaluate={\q=\qss*\i}] in {-1,...,1}{ % EM charge Q
\draw[guide,rotate=\angs-90] (-\Lgrid,\q) -- (\Lgrid,\q);
}
\end{scope}
}
\def\drawGridBaryonTriangle{ % GRID for baryon decuplet
\clip (-1.67,-3.2) rectangle (1.75+1.145/\xs,0.42); % prevent white space
\begin{scope}
\clip[shift={(0,-1)},scale=1.1,rounded corners=4pt] % octagon
(-3/2,1) -- (1.65,1) -- (0,-2) -- cycle;
\foreach \i in {1,2}{
\draw[guide] (-\i/2,-\Lgrid-1) -- (-\i/2,\Lgrid-1); % isospin I3
\draw[guide] ( \i/2,-\Lgrid-1) -- ( \i/2,\Lgrid-1); % isospin I3
}
\foreach \i in {-2,...,1}{
\draw[guide] (-\Lgrid,\i-1) -- (\Lgrid,\i-1); % strangeness S
}
\foreach \i [evaluate={\L=1.2*(\i+6)}] in {-1,...,2}{ % EM charge Q
\draw[guide]
(1/2-\i,0) ++ (\ang+90:0.2*\Lgrid) --++ (\ang-90:\L);
}
\end{scope}
}
\def\drawFullGrid{ % GRID for offset axes
\pgfmathsetmacro\IminGrid{\Imin+1-\Lgrid} % minimum
\pgfmathsetmacro\ImaxGrid{\Imax-1+\Lgrid} % maximum
\pgfmathsetmacro\SminGrid{\Smin+1-\Lgrid} % minimum
\pgfmathsetmacro\SmaxGrid{\Smax-1+\Lgrid} % maximum
\foreach \i [%
parse=true,evaluate={%
\x=\Imin+\i/2;%
\S=max(\Smin-0.2,-\Lgrid+\Smax+2*abs(\x)-1.8);%
}] in {0,...,2*(\Imax-\Imin)}{
\draw[guide] % isospin I3
(\x,\S) -- (\x,\SmaxGrid);
}
\foreach \i [%
parse=true,evaluate={%
\y=\Smin+\i;%
\I=\ImaxGrid-0.5*abs(\y-(\Smin<-2?0:(\Smax+\Smin)/2))-0.23;%
}] in {0,...,\Smax-\Smin}{
\draw[guide] % strangeness S, hypercharge Y
(\IminGrid,\y) -- (\I,\y);
}
\begin{scope}[shift={(0,\Smax-1)}] % vertical shift
\clip %\draw[red]
(\IminGrid,\Lgrid) -- (\IminGrid,\Smin-\Smax+2-\Lgrid)
-- ($(\ang+90:\qs*\Qoffset)+(\ang:-1.1*\qs)$)
--++ (\ang:{(\Qmax-\Qmin+0.2)*\qs}) -- (\ImaxGrid,\Lgrid) -- cycle;
\foreach \i [parse=true,evaluate={\q=\qs*(\Qmin+\i)}] in {0,...,\Qmax-\Qmin}{
\draw[guide] % EM charge Q
($(\ang+90:\qs*\Qoffset)+(\ang:\q)$) --++ (90+\ang:{(\Qoffset-\Lgrid)*(0.12*\i-1.2)});
}
\end{scope}
}
% MACROS for AXES
\def\drawAxisMesonOctet{ % AXES for mesons
\draw[->,thick] (-1-0.15/\xs,0) -- (1+0.22/\xs,0) node[right=-2pt] {$I_3$};
\draw[->,thick] (0,-1.15) -- (0,1.22) node[above=-2] {$S$};
\draw[->,thick] (\ang:-\qs*1.15) -- (\ang:\qs*1.26)
node[rotate=\angt,anchor=\angs+174,inner sep=0.5pt] {$Q=I_3+\frac{1}{2}S$};
\begin{scope}[every node/.style={tick}] % ticks
\tick{-1,0}{90} node[left=3pt,below=1pt] {$-1$};
\tick{-1/2,0}{90}; %node[left=5pt,below] {$-\frac{1}{2}$};
\tick{1/2,0}{90}; %node[left=3pt,below] {$+\frac{1}{2}$};
\tick{1,0}{90} node[right=3pt,below] {$+1$};
\tick{0,-1}{0} node[left=5pt,below=1pt] {$-1$};
\tick{0,-1/2}{0};
\tick{0,1/2}{0};
\tick{0,1}{0} node[left=5pt,above=0.8pt] {$+1$};
\qtick{1/2};
%\qtick{-1} node[anchor=\ang+5] {$-1$}; % vertical
\qtick{-1} node[rotate=\angl,below left=0pt] {$-1$};
\qtick{-1/2};
%\qtick{0} node[below right=0] {$0$}; % vertical
\qtick{0} node[rotate=\angl,right=0.5pt,below=1pt] {$0$};
\qtick{1/2};
%\qtick{1} node[anchor=\ang+160] {$+1$}; % vertical
\qtick{1} node[rotate=\angl,below left=0pt] {$+1$};
\end{scope}
}
\def\drawAxisBaryonOctet{ % AXES for baryons octet
\draw[->,thick] (-1-0.15/\xs,0) -- (1+0.22/\xs,0)
node[anchor=-140,inner sep=1pt] {$I_3$};
\draw[->,thick] (0,-2.15) -- (0,0.22)
node[above=-2] {$S$};
\draw[->,thick,shift={(0,-1)}] (\ang:-\qs*1.15) -- (\ang:\qs*1.26)
node[rotate=\angt,anchor=-168,inner sep=0pt] {$Q=I_3+\frac{1}{2}(B+S)$};
\begin{scope}[every node/.style={tick}] % ticks
\node[below left=1pt] at (0,0) {$0$};
\tick{-1,0}{90} node[left=3pt,below=1pt] {$-1$};
\tick{-1/2,0}{90}; %node[left=5pt,below] {$-\frac{1}{2}$};
\tick{1/2,0}{90}; %node[left=3pt,below] {$+\frac{1}{2}$};
\tick{1,0}{90} node[left=3pt,below=1pt] {$+1$};
\tick{0,-1/2}{0};
\tick{0,-1}{0} node[above=2pt,left=0pt] {$-1$};
\tick{0,-3/2}{0};
\tick{0,-2}{0} node[left=5pt,below=1.0pt] {$-2$};
\begin{scope}[shift={(0,-1)}]
\qtick{1/2};
%\qtick{-1} node[anchor=\ang+5] {$-1$};
\qtick{-1} node[rotate=\angl,below left=0pt] {$-1$}; % vertical
\qtick{-1/2};
%\qtick{0} node[below right=0] {$0$}; % vertical
\qtick{0} node[rotate=\angl,right=0.5pt,below=1pt] {$0$};
\qtick{1/2};
%\qtick{1} node[anchor=\ang+160] {$+1$}; % vertical
\qtick{1} node[rotate=\angl,below left=0pt] {$+1$};
\end{scope}
\end{scope}
}
\def\drawAxisBaryonDecuplet{ % AXES for baryon decuplet
\draw[->,thick] (-1.5-0.15/\xs,0) -- (1.5+0.25/\xs,0)
node[anchor=-150,inner sep=2pt] {$I_3$};
\draw[->,thick] (0,-3.15) -- (0,0.22)
node[above=-2] {$S$};
\draw[->,thick,shift={(0,-1)}] (\ang:-\qs*1.2) -- (\ang:\qs*2.2)
%node[rotate=\angt,anchor=179,inner sep=2pt] {$Q=I_3+\frac{1}{2}(B+S)$};
node[rotate=\angt,anchor=125,inner sep=12pt] {$Q=I_3+\frac{1}{2}(B+S)$};
\begin{scope}[every node/.style={tick}] % ticks
\node[below left=1pt] at (0,0) {$0$};
\tick{-3/2,0}{90};
\tick{-1,0}{90} node[left=3pt,below=1pt] at (-1,-\ltick) {$-1$};
\tick{-1/2,0}{90}; %node[left=3pt,below] {$-\frac{1}{2}$};
\tick{1/2,0}{90}; %node[left=3pt,below] {$+\frac{1}{2}$};
\tick{1,0}{90} node[left=3pt,below=1pt] {$+1$};
\tick{3/2,0}{90};
\tick{0,-1/2}{0};
\tick{0,-1}{0} node[above=2pt,left=0pt] {$-1$};
\tick{0,-3/2}{0};
\tick{0,-2}{0} node[left=1pt] {$-2$};
\tick{0,-5/2}{0};
\tick{0,-3}{0} node[left=1pt] {$-3$};
\begin{scope}[shift={(0,-1)}]
\qtick{1/2};
%\qtick{-1} node[anchor=\ang+20,inner sep=2pt] {$-1$}; {$-1$}; % vertical
\qtick{-1} node[rotate=\angl,below left=0pt] {$-1$};
\qtick{-1/2};
%\qtick{0} node[below right=0] {$0$}; % vertical
\qtick{0} node[rotate=\angl,right=0.5pt,below=1pt] {$0$};
\qtick{1/2};
%\qtick{1} node[anchor=\ang+70,inner sep=2pt] {$+1$}; % vertical
\qtick{1} node[rotate=\angl,left=3pt,below=1pt] {$+1$};
\qtick{3/2};
%\qtick{2} node[anchor=\ang+70,inner sep=2pt] {$+2$}; % vertical
\qtick{2} node[rotate=\angl,left=3pt,below=1pt] {$+2$};
\end{scope}
\end{scope}
}
\def\drawSAxis{ % offset S AXES (vertical)
\begin{scope}[shift={(\Imin+1-\Lgrid,0)},every node/.style={tick}] % ticks
\draw[->,thick] (0,\Smin-0.15) -- (0,\Smax+0.22) node[above=2pt] {$S$};
\foreach \i [parse=true,evaluate={%
\y=\Smin+\i/2; % tick position
\num=int(abs(2*\y)); % numerator for denominator = 2
}] in {0,...,2*(\Smax-\Smin)}{
\ifodd\num % half-integer tick
%\ifdim \y pt < 0 pt - \else + \fi % sign
%\dfrac{\pgfmathprintnumber{\num}}{2} % fraction
\else % whole integer tick
\tick{0,\y}{0} node[left=1pt] {$
\ifnum \num=0 0 \else \pgfmathprintnumber[print sign=true]{\y} \fi
$};
\fi
}
\end{scope}
}
\def\drawIAxis{ % offset I3 AXES (horizontal)
\begin{scope}[shift={(0,\Lgrid+\Smax-1)},every node/.style={tick}] % vertical shift
\draw[->,thick] (\Imin-0.15/\xs,0) -- (\Imax+0.22/\xs,0) node[right=2pt] {$I_3$};
\foreach \i [parse=true,evaluate={%
\x=\Imin+\i/2; % tick position
\num=int(2*\x); % numerator for denominator = 2
}] in {0,...,2*(\Imax-\Imin)}{
\ifodd\num % half-integer tick
\tick{\x,0}{-90} node[left=3pt,above=0pt] {$
\pgfmathprintnumber[print sign=true]{\num}/2 % fraction
$};
\else % whole integer tick
\tick{\x,0}{-90} node[left={(\x!=0)*3pt},above=1pt] {$
\ifnum \num=0 0 \else \pgfmathprintnumber[print sign=true]{\x} \fi
$};
\fi
}
\end{scope}
}
\def\drawQAxis{ % offset I3 AXES (diagonal)
\begin{scope}[shift={($(\ang+90:\qs*\Qoffset)+(0,\Smax-1)$)},every node/.style={tick}] % shift
\draw[->,thick] (\ang:{\qs*(\Qmin-0.15)}) -- (\ang:{\qs*(\Qmax+0.26)});
\node[rotate=\angt,below=15pt] at (\ang:\qs*\Qmax) {$Q=I_3+\frac{1}{2}S$};
\foreach \i [parse=true,evaluate={%
\q=\Qmin+\i/2; % tick position
\num=int(2*\q); % numerator for denominator = 2
}] in {0,...,2*(\Qmax-\Qmin)}{
\ifodd\num
\qtick{\q};
\else % whole integer tick
\qtick{\q} node[anchor=\ang+70,inner sep=2pt] {$
\ifnum \num=0 \;0 \else \pgfmathprintnumber[print sign=true]{\q} \fi
$};
\fi
}
\end{scope}
}
% MACROS for drawing REGULAR SHAPES
\def\drawOctagon{ % MESONS OCTAGON
\coordinate (Q-1) at (\ang:-\qs); % Q = -1
\coordinate (Q+1) at (\ang:\qs); % Q = +1
\draw[myblue,very thick]
(1,0) -- (1/2,-1) -- (\lmask,-1)
(-\lmask,-1) -- (-1/2,-1) -- ($(Q-1)+(\angs-90:\lqmask)$)
($(Q-1)+(\angs+90:\lqmask)$) -- (-1,0) -- (-1/2,1) -- (-\lmask,1)
(\lmask,1) -- (1/2,1) -- ($(Q+1)+(\angs+90:\lqmask)$)
($(Q+1)+(\angs-90:\lqmask)$) -- (1,0);
}
\def\drawBaryonOctagon{ % BARYON OCTAGON
\coordinate (Q-1) at ($(0,-1)+(\ang:-\qs)$); % Q = -1
\coordinate (Q+1) at ($(0,-1)+(\ang:\qs)$); % Q = +1
\draw[myblue,very thick]
(-1/2,0) -- (1/2,0) -- ($(Q+1)+(\angs+90:\lqmask)$)
($(Q+1)+(\angs-90:\lqmask)$) -- (1,-1) -- (1/2,-2) -- (\lmask,-2)
(-\lmask,-2) -- (-1/2,-2) -- ($(Q-1)+(\angs-90:\lqmask)$)
($(Q-1)+(\angs+90:\lqmask)$) -- (-1,-1) -- (-1/2,0);
}
\def\drawBaryonTriangle{ % BARYON TRIANGLE
\coordinate (Q-1) at ($(0,-1)+(\ang:-\qs)$); % Q = -1
\draw[myblue,very thick]
(-3/2,0) -- (3/2,0) -- (0,-3) -- ($(Q-1)+(\angs-90:\lqmask)$)
($(Q-1)+(\angs+90:\lqmask)$) -- (-3/2,0);
}
\begin{document}
% PSEUDOSCALAR MESON OCTET / NONET
\foreach \xs [evaluate=\xs] in {2/sqrt(3)}{ % loop over xscale
\begin{tikzpicture}[scale=1.8,x={\xs cm},y=1cm]
\message{^^JPseudoscalar meson octet (xs = \xs)}
\computeParameters
% AXES & GRID
\drawGrid{0}
\drawAxisMesonOctet
% OCTAGON
\drawOctagon
% MESONS
\particle(-1/2, 1) node[anchor=-70,inner sep=4pt] {K$^0$};
\particle( 1/2, 1) node[anchor=-130,inner sep=4pt] {K$^+$};
\particle(-1, 0) node[anchor=-70,inner sep=4pt] {$\PGp^-$};
\particle( 1, 0) node[anchor=-130,inner sep=4pt] {$\PGp^+$};
\particle(-1/2,-1) node[anchor=50,inner sep=2pt] {K$^-$};
\particle( 1/2,-1) node[anchor=155,inner sep=4pt] {$\bar{K}^0$};
\particle(\ang+30:0.09) node[anchor=-120,inner sep=4pt] {$\PGp^0$};
%\particle(\ang/2:0.12) node[anchor=\ang/2-180,inner sep=5pt] {$\PGp^0$};
\particle(120:0.09) node[anchor=-50,inner sep=2.5pt] {$\PGe$};
\particle(240:0.09) node[anchor= 60,inner sep=3pt] {$\PGe'$};
\end{tikzpicture}} % end loop
% PSEUDOSCALAR MESON OCTET / NONET (offset axes)
\foreach \xs [evaluate=\xs] in {2/sqrt(3)}{ % loop over xscale
\begin{tikzpicture}[scale=1.7,x={\xs cm},y=1cm]
\message{^^JPseudoscalar meson octet (xs = \xs)}
\computeParameters
% AXES & GRID
\drawFullGrid
\drawSAxis
\drawIAxis
\drawQAxis
% OCTAGON
\draw[myblue,very thick]
(1,0) -- (1/2,-1) -- (-1/2,-1) -- (-1,0)
-- (-1/2,1) -- (1/2,1) -- cycle;
% MESONS
\particle(-1/2, 1) node[anchor=-70,inner sep=4pt] {K$^0$};
\particle( 1/2, 1) node[anchor=-130,inner sep=4pt] {K$^+$};
\particle(-1, 0) node[anchor=-10,inner sep=2pt] {$\PGp^-$};
\particle( 1, 0) node[anchor=-170,inner sep=4pt] {$\PGp^+$};
\particle(-1/2,-1) node[anchor=50,inner sep=2pt] {K$^-$};
\particle( 1/2,-1) node[anchor=155,inner sep=4pt] {$\bar{K}^0$};
\particle(90:0.05) node[anchor=-100,inner sep=4pt] {$\PGp^0$};
\particle(210:0.05) node[anchor=45,inner sep=3pt] {$\PGe$};
\particle(330:0.05) node[anchor=150,inner sep=3pt] {$\PGe'$};
\end{tikzpicture}} % end loop
% PSEUDOSCALAR MESON OCTET / NONET (offset axes, quarks)
% https://commons.wikimedia.org/wiki/File:Meson-octet-small.svg
\foreach \xs [evaluate=\xs] in {2/sqrt(3)}{ % loop over xscale
\begin{tikzpicture}[scale=1.7,x={\xs cm},y=1cm]
\message{^^JPseudoscalar meson octet (xs = \xs)}
\computeParameters
% AXES & GRID
\drawFullGrid
\drawSAxis
\drawIAxis
\drawQAxis
% OCTAGON
\draw[myblue,very thick]
(1,0) -- (1/2,-1) -- (-1/2,-1) -- (-1,0)
-- (-1/2,1) -- (1/2,1) -- cycle;
% MESONS
\mesonNode(-1/2, 1) {\PM{d}{u}}
node[pname=0,anchor=-60] at (P.120) {K$^0$};
\mesonNode( 1/2, 1) {\PM{d}{u}}
node[pname=1.5,anchor=-140] at (P.40) {K$^+$};
\mesonNode(-1, 0) {\PM{d}{u}}
node[pname=-1,anchor=-60] at (P.120) {$\PGp^-$};
\mesonNode( 1, 0) {\PM{d}{u}}
node[pname=1,anchor=-140] at (P.40) {$\PGp^+$};
\mesonNode(-1/2,-1) {\PM{d}{u}}
node[pname,anchor=40] at (P.-140) {K$^-$};
\mesonNode( 1/2,-1) {\PM{d}{u}}
node[pname,anchor=150] at (P.-30) {$\bar{K}^0$};
\node[particle=25pt] (P) at (0,0) {}
node[pname=1.4,anchor=-100] at (P.70) {$\PGp^0$}
node[pname=0.8,anchor=45] at (P.-145) {$\PGe$}
node[pname=0.5,anchor=150] at (P.-30) {$\PGe'$};
\node[myred,scale=0.9,anchor=-68,inner sep=1.9pt]
at (P) {\PM{d}{d}};
\node[myred,scale=0.9,anchor=40,inner sep=0.3pt]
at (P) {\PM{u}{u}};
\node[myred,scale=0.9,anchor=172,inner sep=2.7pt]
at (P) {\PM{s}{s}};
\end{tikzpicture}} % end loop
% VECTOR MESON OCTET / NONET
\foreach \xs [evaluate=\xs] in {2/sqrt(3)}{ % loop over xscale
\begin{tikzpicture}[scale=1.8,x={\xs cm},y=1cm]
\message{^^J^^JVector meson octet (xs = \xs)}
\computeParameters
% AXES & GRID
\drawGrid{0}
\drawAxisMesonOctet
% OCTAGON
\drawOctagon
% MESONS
\particle(-1/2, 1) node[anchor=-70,inner sep=4pt] {K$^{*0}$};
\particle( 1/2, 1) node[anchor=-130,inner sep=4pt] {K$^{*+}$};
\particle(-1, 0) node[anchor=-70,inner sep=4pt] {$\PGr^-$};
\particle( 1, 0) node[anchor=-130,inner sep=4pt] {$\PGr^+$};
\particle(-1/2,-1) node[anchor=60,inner sep=4pt] {K$^{*-}$};
\particle( 1/2,-1) node[anchor=150,inner sep=3pt] {$\bar{K}^{*0}$};
\particle(\ang+30:0.09) node[anchor=-130,inner sep=3pt] {$\PGr^0$};
\particle(120:0.09) node[anchor=-50,inner sep=2pt] {$\PGf$};
\particle(240:0.09) node[anchor=58,inner sep=3pt] {$\PGo$};
\end{tikzpicture}} % end loop
% VECTOR MESON OCTET / NONET (offset axes)
\foreach \xs [evaluate=\xs] in {2/sqrt(3)}{ % loop over xscale
\begin{tikzpicture}[scale=1.7,x={\xs cm},y=1cm]
\message{^^JPseudoscalar meson octet (xs = \xs)}
\computeParameters
% AXES & GRID
\drawFullGrid
\drawSAxis
\drawIAxis
\drawQAxis
% OCTAGON
\draw[myblue,very thick]
(1,0) -- (1/2,-1) -- (-1/2,-1) -- (-1,0)
-- (-1/2,1) -- (1/2,1) -- cycle;
% MESONS
\particle(-1/2, 1) node[anchor=-70,inner sep=4pt] {K$^{*0}$};
\particle( 1/2, 1) node[anchor=-130,inner sep=4pt] {K$^{*+}$};
\particle(-1, 0) node[anchor=-10,inner sep=3pt] {$\PGr^-$};
\particle( 1, 0) node[anchor=-170,inner sep=4pt] {$\PGr^+$};
\particle(-1/2,-1) node[anchor=60,inner sep=4pt] {K$^{*-}$};
\particle( 1/2,-1) node[anchor=150,inner sep=3pt] {$\bar{K}^{*0}$};
\particle(90:0.05) node[anchor=-100,inner sep=4pt] {$\PGr^0$};
\particle(210:0.05) node[anchor=45,inner sep=3pt] {$\PGo$};
\particle(330:0.05) node[anchor=140,inner sep=3pt] {$\PGf$};
\end{tikzpicture}} % end loop
% VECTOR MESON OCTET / NONET (offset axes, quarks)
% https://commons.wikimedia.org/wiki/File:Meson-octet-small.svg
\foreach \xs [evaluate=\xs] in {2/sqrt(3)}{ % loop over xscale
\begin{tikzpicture}[scale=1.7,x={\xs cm},y=1cm]
\message{^^JPseudoscalar meson octet (xs = \xs)}
\computeParameters
% AXES & GRID
\def\Qoffset{-1.8}
\drawFullGrid
\drawSAxis
\drawIAxis
\drawQAxis
% OCTAGON
\draw[myblue,very thick]
(1,0) -- (1/2,-1) -- (-1/2,-1) -- (-1,0)
-- (-1/2,1) -- (1/2,1) -- cycle;
% MESONS
\mesonNode(-1/2, 1) {\PM{d}{u}}
node[pname=0,anchor=-50] at (P.130) {K$^{*0}$};
\mesonNode( 1/2, 1) {\PM{d}{u}}
node[pname=1.5,anchor=-150] at (P.30) {K$^{*+}$};
\mesonNode(-1, 0) {\PM{d}{u}}
node[pname=-1,anchor=-60] at (P.120) {$\PGr^-$};
\mesonNode( 1, 0) {\PM{d}{u}}
node[pname=1,anchor=-140] at (P.40) {$\PGr^+$};r
\mesonNode(-1/2,-1) {\PM{d}{u}}
node[pname,anchor=40] at (P.-140) {K$^{*-}$};
\mesonNode( 1/2,-1) {\PM{d}{u}}
node[pname,anchor=154] at (P.-26) {$\bar{K}^{*0}$};
\node[particle=25pt] (P) at (0,0) {}
node[pname=1.2,anchor=-100] at (P.70) {$\PGr^0$}
node[pname=0.8,anchor=45] at (P.-145) {$\PGo$}
node[pname=0.0,anchor=145] at (P.-35) {$\PGf$};
\node[myred,scale=0.9,anchor=-68,inner sep=1.9pt]
at (P) {\PM{d}{d}};
\node[myred,scale=0.9,anchor=40,inner sep=0.3pt]
at (P) {\PM{u}{u}};
\node[myred,scale=0.9,anchor=172,inner sep=2.7pt]
at (P) {\PM{s}{s}};
\end{tikzpicture}} % end loop
% BARYON OCTET
\foreach \xs [evaluate=\xs] in {2/sqrt(3)}{ % loop over xscale
\begin{tikzpicture}[scale=1.8,x={\xs cm},y=1cm]
\message{^^J^^JBaryon octet (xs = \xs)}
\computeParameters
% AXES & GRID
\drawGrid{-1}
\drawAxisBaryonOctet
% OCTAGON
\drawBaryonOctagon
% BARYONS
\particle(-1/2, 0) node[anchor=-70,inner sep=4pt] {n$^0$};
\particle( 1/2, 0) node[anchor=-140,inner sep=3pt] {p$^+$};
\particle(-1, -1) node[anchor=-20,inner sep=2pt] {$\Sigma^-$};
\particle({$(60:0.09)+(0,-1)$})
node[anchor=-130,inner sep=3pt] {$\Sigma^0$};
\particle({$(-120:0.09)+(0,-1)$})
node[anchor=60,inner sep=3pt] {$\Lambda^0$};
\particle( 1, -1) node[anchor=-160,inner sep=4pt] {$\Sigma^+$};
\particle(-1/2,-2) node[anchor=50,inner sep=2pt] {$\Xi^-$};
\particle( 1/2,-2) node[anchor=140,inner sep=2pt] {$\Xi^0$};
\end{tikzpicture}} % end loop
% PSEUDOSCALAR BARYON OCTET (offset axes)
\foreach \xs [evaluate=\xs] in {2/sqrt(3)}{ % loop over xscale
\begin{tikzpicture}[scale=1.7,x={\xs cm},y=1cm]
\message{^^J^^JBaryon octet (xs = \xs), offset}
\computeParameters
% AXES & GRID
\def\Smin{-2} \def\Smax{0} % S axis limits
\def\Imin{-1} \def\Imax{1} % I3 axis limits
\def\Qmin{-1} \def\Qmax{1} % Q axis limits
\drawFullGrid
\drawSAxis
\drawIAxis
\drawQAxis
% OCTAGON
\draw[myblue,very thick]
(1,-1) -- (1/2,-2) -- (-1/2,-2) -- (-1,-1)
-- (-1/2,0) -- (1/2,0) -- cycle;
% BARYONS
\particle(-1/2, 0) node[anchor=-70,inner sep=4pt] {n$^0$};
\particle( 1/2, 0) node[anchor=-140,inner sep=3pt] {p$^+$};
\particle(-1, -1) node[anchor=-10,inner sep=3pt] {$\Sigma^-$};
\particle({$(60:0.05)+(0,-1)$})
node[anchor=-120,inner sep=4pt] {$\Sigma^0$};
\particle({$(-120:0.05)+(0,-1)$})
node[anchor=80,inner sep=4pt] {$\Lambda^0$};
\particle( 1, -1) node[anchor=-170,inner sep=4pt] {$\Sigma^+$};
\particle(-1/2,-2) node[anchor=50,inner sep=2pt] {$\Xi^-$};
\particle( 1/2,-2) node[anchor=140,inner sep=2pt] {$\Xi^0$};
\end{tikzpicture}} % end loop
% PSEUDOSCALAR BARYON OCTET (offset axes)
\foreach \xs [evaluate=\xs] in {2/sqrt(3)}{ % loop over xscale
\begin{tikzpicture}[scale=1.7,x={\xs cm},y=1cm]
\message{^^J^^JBaryon octet (xs = \xs), offset}
\computeParameters
% AXES & GRID
\def\Smin{-2} \def\Smax{0} % S axis limits
\def\Imin{-1} \def\Imax{1} % I3 axis limits
\def\Qmin{-1} \def\Qmax{1} % Q axis limits
\def\Qoffset{-1.8}
\drawFullGrid
\drawSAxis
\drawIAxis
\drawQAxis
% OCTAGON
\draw[myblue,very thick]
(1,-1) -- (1/2,-2) -- (-1/2,-2) -- (-1,-1)
-- (-1/2,0) -- (1/2,0) -- cycle;
% BARYONS
\baryonNode(-1/2, 0) {dd\\u}
node[pname=0,anchor=-70] at (P.120) {n$^0$};
\baryonNode( 1/2, 0) {uu\\d}
node[pname=1,anchor=-130] at (P.40) {p$^+$};
\baryonNode(-1, -1) {dd\\s}
node[pname=-1,anchor=-50] at (P.140) {$\Sigma^-$};
\baryonNode( 0, -1) {ud\\s}
node[pname=2,anchor=-120] at (P.50) {$\Sigma^0$}
node[pname=0,anchor=40] at (P.-120) {$\Lambda^0$};
\baryonNode( 1, -1) {uu\\s}
node[pname=1,anchor=-140] at (P.30) {$\Sigma^+$};
\baryonNode(-1/2,-2) {ds\\s}
node[pname=-1,anchor=30] at (P.-150) {$\Xi^-$};
\baryonNode( 1/2,-2) {us\\s}
node[pname,anchor=150] at (P.-30) {$\Xi^0$};
\end{tikzpicture}} % end loop
% BARYON DECUPLET
\foreach \xs [evaluate=\xs] in {2/sqrt(3)}{ % loop over xscale
\begin{tikzpicture}[scale=1.8,x={\xs cm},y=1cm]
\message{^^J^^JBaryon decuplet (xs = \xs)}
\computeParameters
% AXES & GRID
\drawGridBaryonTriangle
\drawAxisBaryonDecuplet
% TRIANGLE
\drawBaryonTriangle
% BARYONS
\particle(-3/2, 0) node[anchor=-110,inner sep=4pt] {$\Delta^-$};
\particle(-1/2, 0) node[anchor=-100,inner sep=4pt] {$\Delta^0$};
\particle( 1/2, 0) node[anchor=-115,inner sep=4pt] {$\Delta^+$};
\particle( 3/2, 0) node[anchor=-80,inner sep=4pt] {$\Delta^{++}$};
\particle(-1, -1) node[anchor=25,inner sep=1pt] {$\Sigma^{*-}$};
\particle( 0, -1) node[anchor=-136,inner sep=5pt] {$\Sigma^{*0}$};
\particle( 1, -1) node[anchor=160,inner sep=4pt] {$\Sigma^{*+}$};
\particle(-1/2,-2) node[anchor=25,inner sep=1pt] {$\Xi^{*-}$};
\particle( 1/2,-2) node[anchor=160,inner sep=4pt] {$\Xi^{*0}$};
\particle( 0, -3) node[anchor=160,inner sep=4pt] {$\Omega^-$};
\end{tikzpicture}} % end loop
% BARYON DECUPLET (offset axes)
\foreach \xs [evaluate=\xs] in {2/sqrt(3)}{ % loop over xscale
\begin{tikzpicture}[scale=1.7,x={\xs cm},y=1cm]
\message{^^J^^JBaryon decuplet (xs = \xs)}
\computeParameters
% AXES & GRID
\def\Smin{-3} \def\Smax{0} % S axis limits
\def\Imin{-1.5} \def\Imax{1.5} % I3 axis limits
\def\Qmin{-1} \def\Qmax{2} % Q axis limits
\def\Qoffset{-2.45}
\drawFullGrid
\drawSAxis
\drawIAxis
\drawQAxis
% OCTAGON
\draw[myblue,very thick]
(-3/2,0) -- (3/2,0) -- (0,-3) -- cycle;
% BARYONS
\particle(-3/2, 0) node[anchor=-90,inner sep=4pt] {$\Delta^-$};
\particle(-1/2, 0) node[anchor=-100,inner sep=4pt] {$\Delta^0$};
\particle( 1/2, 0) node[anchor=-115,inner sep=4pt] {$\Delta^+$};
\particle( 3/2, 0) node[anchor=-120,inner sep=4pt] {$\Delta^{++}$};
\particle(-1, -1) node[anchor=25,inner sep=1pt] {$\Sigma^{*-}$};
\particle( 0, -1) node[anchor=120,inner sep=3pt] {$\Sigma^0$};
\particle( 1, -1) node[anchor=160,inner sep=4pt] {$\Sigma^{*+}$};
\particle(-1/2,-2) node[anchor=25,inner sep=1pt] {$\Xi^{*-}$};
\particle( 1/2,-2) node[anchor=160,inner sep=4pt] {$\Xi^{*0}$};
\particle( 0, -3) node[anchor=110,inner sep=4pt] {$\Omega^-$};
\end{tikzpicture}} % end loop
% BARYON DECUPLET (offset axes)
\foreach \xs [evaluate=\xs] in {2/sqrt(3)}{ % loop over xscale
\begin{tikzpicture}[scale=1.7,x={\xs cm},y=1cm]
\message{^^J^^JBaryon decuplet (xs = \xs)}
\computeParameters
% AXES & GRID
\def\Smin{-3} \def\Smax{0} % S axis limits
\def\Imin{-1.5} \def\Imax{1.5} % I3 axis limits
\def\Qmin{-1} \def\Qmax{2} % Q axis limits
\def\Qoffset{-2.45}
\drawFullGrid
\drawSAxis
\drawIAxis
\drawQAxis
% OCTAGON
\draw[myblue,very thick]
(-3/2,0) -- (3/2,0) -- (0,-3) -- cycle;
% BARYONS
\baryonNode(-3/2, 0) {dd\\d}
node[pname,anchor=-60] at (P.130) {$\Delta^-$};
\baryonNode(-1/2, 0) {dd\\u}
node[pname,anchor=-60] at (P.130) {$\Delta^0$};
\baryonNode( 1/2, 0) {uu\\d}
node[pname=1,anchor=-145] at (P.40) {$\Delta^+$};
\baryonNode( 3/2, 0) {uu\\u}
node[pname=2,anchor=-150] at (P.30) {$\Delta^{++}$};
\baryonNode(-1, -1) {dd\\s}
node[pname,anchor=20] at (P.-160) {$\Sigma^{*-}$};
\baryonNode( 0, -1) {ud\\s}
node[pname,anchor=160] at (P.-30) {$\Sigma^0$};
\baryonNode( 1, -1) {uu\\s}
node[pname,anchor=160] at (P.-20) {$\Sigma^{*+}$};
\baryonNode(-1/2,-2) {ds\\s}
node[pname,anchor=20] at (P.-160) {$\Xi^{*-}$};
\baryonNode( 1/2,-2) {us\\s}
node[pname,anchor=160] at (P.-20) {$\Xi^{*0}$};
\baryonNode( 0, -3) {ss\\s}
node[pname,anchor=60] at (P.-120) {$\Omega^-$};
\end{tikzpicture}} % end loop
\end{document}
Click to download: SM_isospin.tex • SM_isospin.pdf
Open in Overleaf: SM_isospin.tex



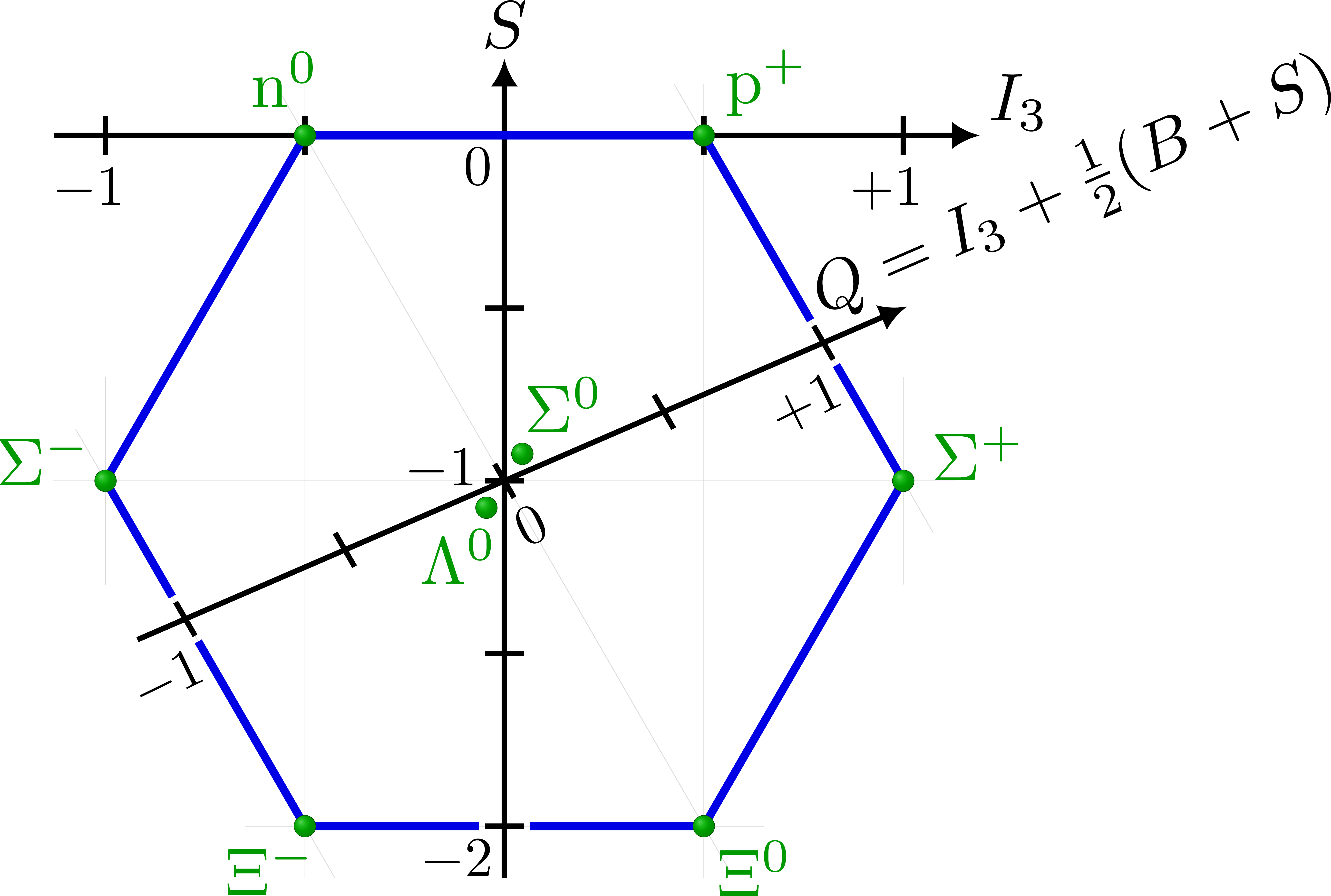
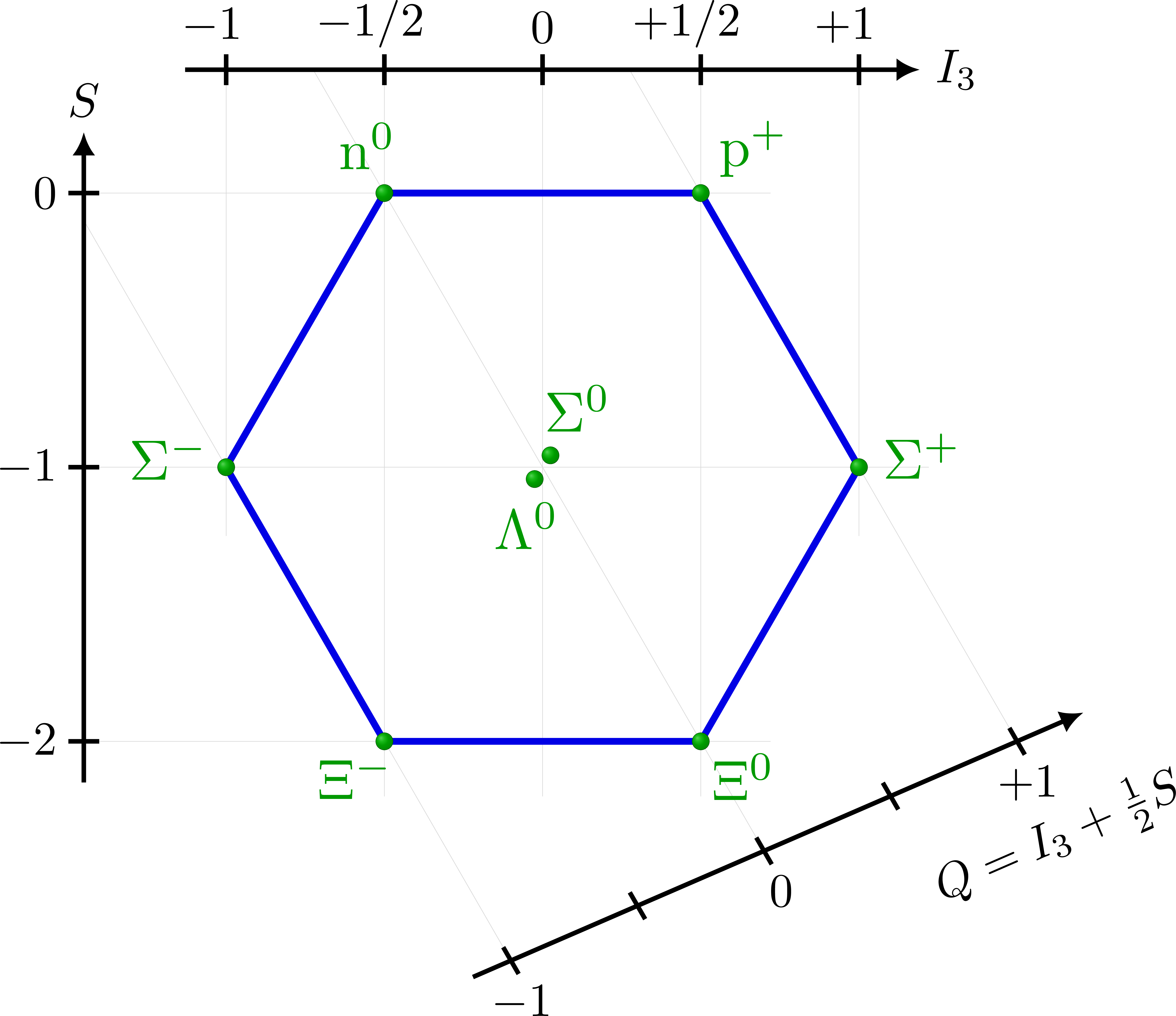
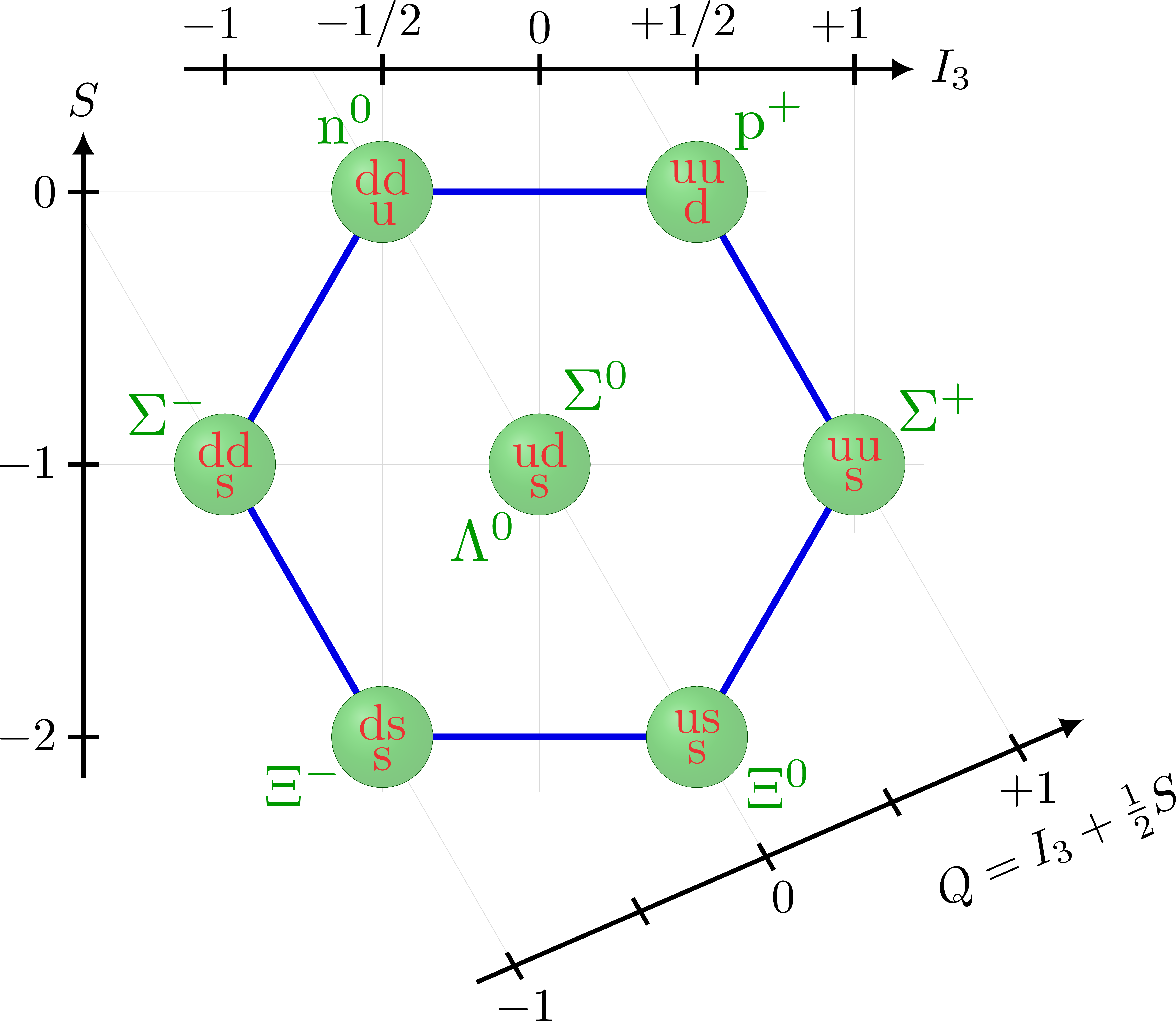
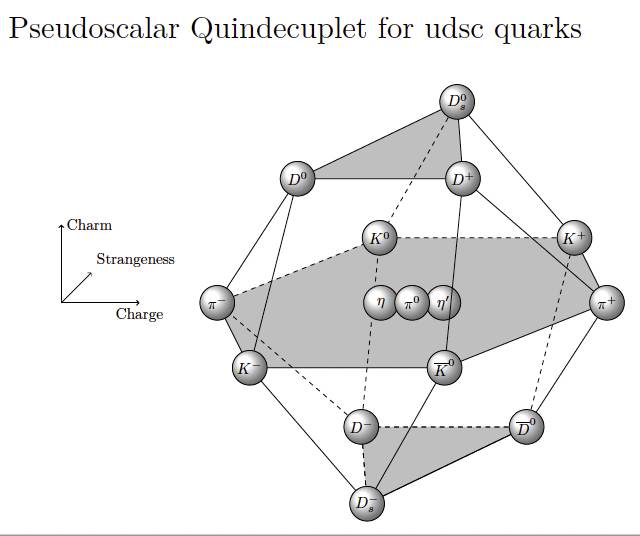
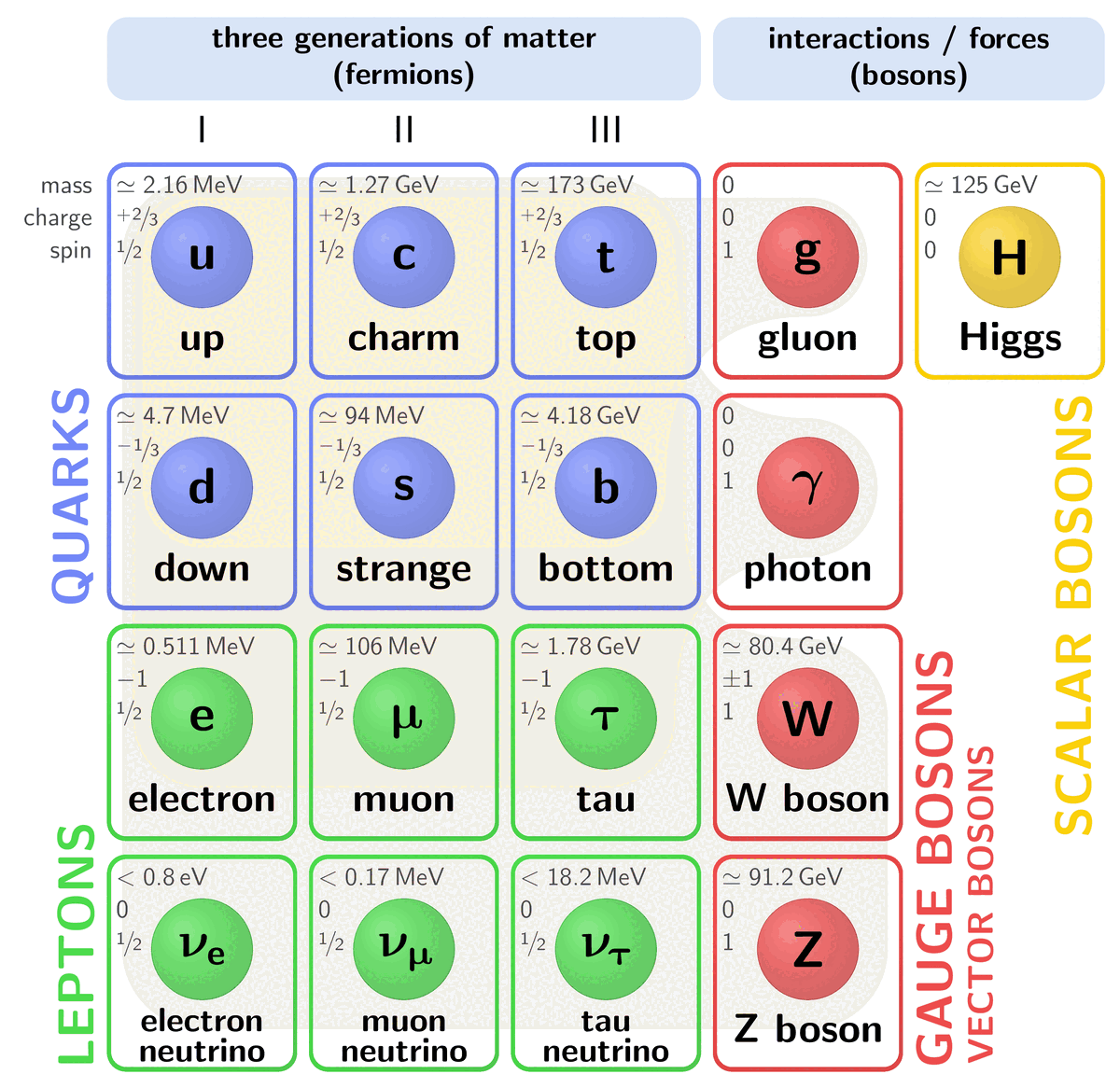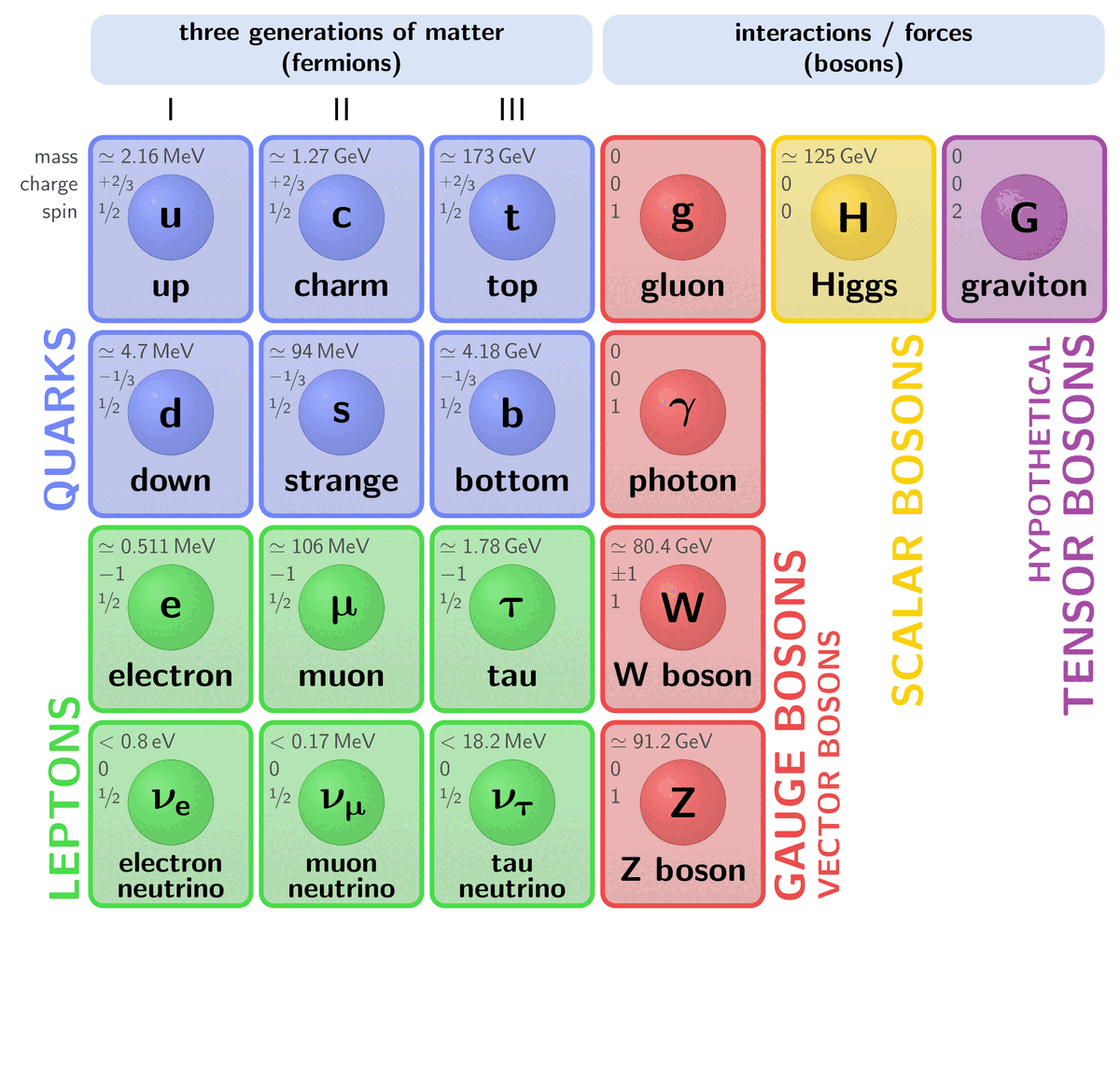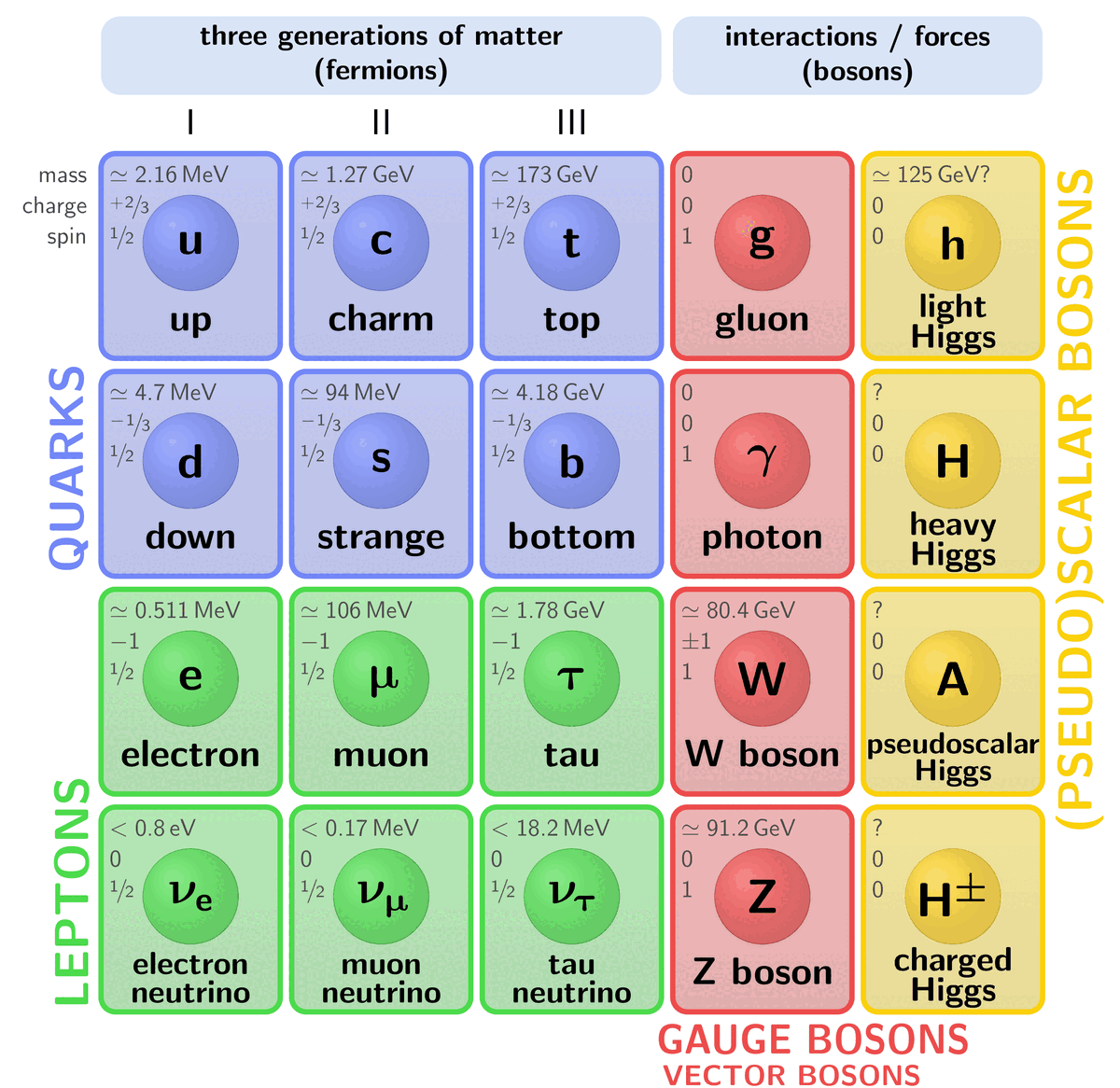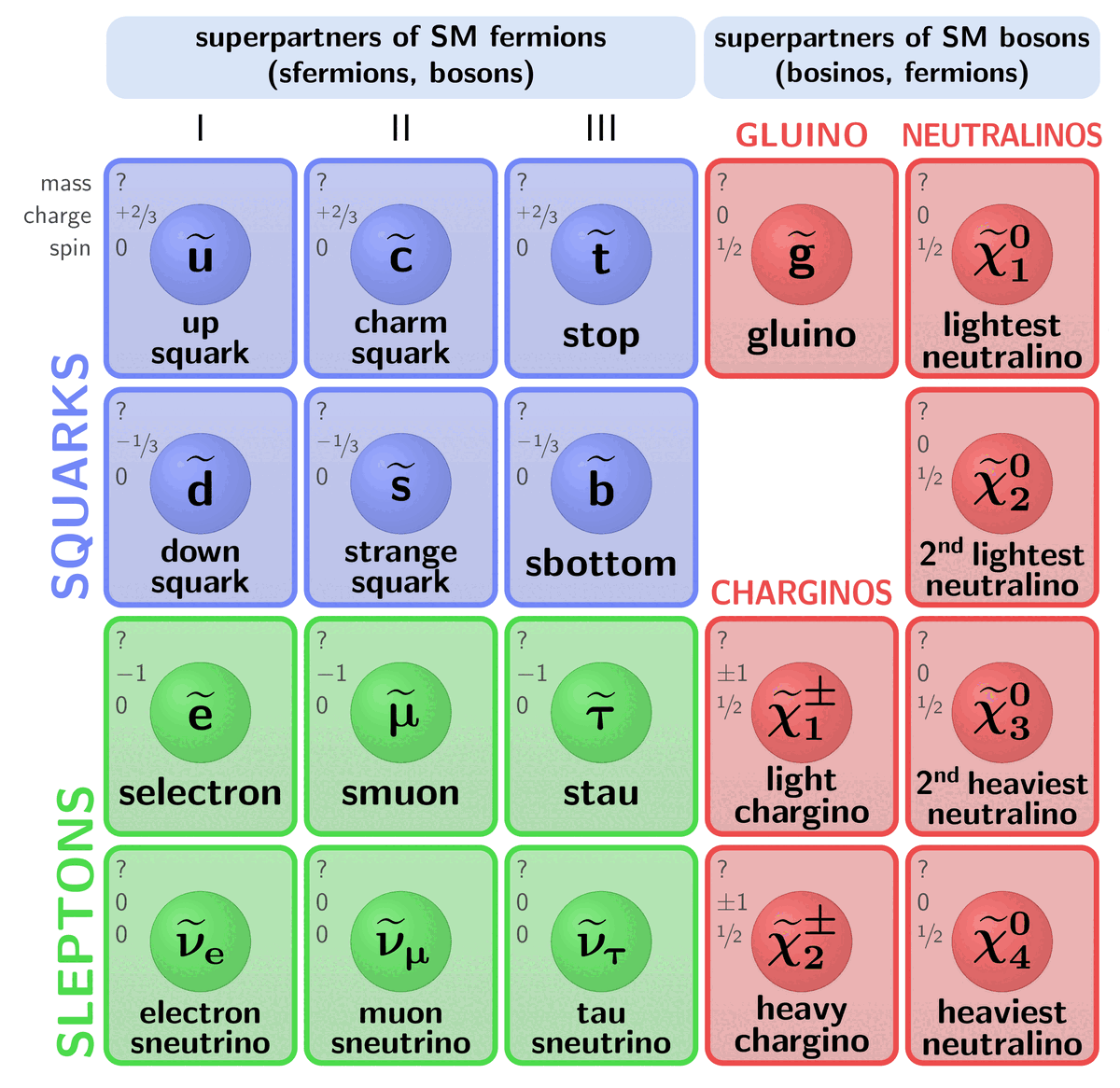
In Baryon octet, \Sigma^- particle should have dds quark contents so {\Sigma^-}/{dds}, but it’s wrongly labelled as ddd.
Thank you for pointing it out, Sabin! It should be fixed now.