Branch and Bound

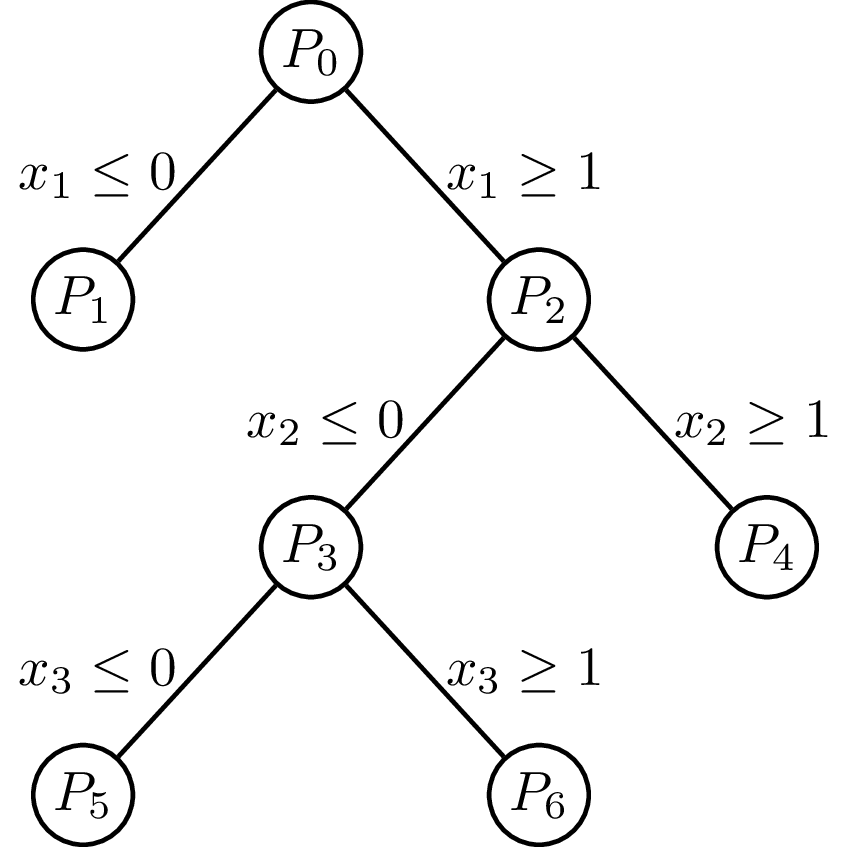
Illustration of a linear-programming (LP)-based branch and bound algorithm. Not knowing how to solve a mixed-integer programming (MIP) problem directly, it first removes all integrality constraints. This results in a solvable LP called the linear-programming relaxation of the original MIP. The algorithm then picks some variable x restricted to be integer, but whose value in the LP relaxation is fractional. Suppose its value in the LP relaxation is x = 0.7. It then excludes this value by imposing the restrictions x ≤ 0 and x ≥ 1, thereby creating two new MIPs. By applying this recursively step and exploring each resulting bifurcation, the globally optimal solution satisfying all constraints can be found.

Edit and compile if you like:

% Illustration of a linear-programming (LP)-based branch and bound algorithm. Not knowing how to solve a mixed-integer programming (MIP) problem directly, it first removes all integrality constraints. This results in a solvable LP called the linear-programming relaxation of the original MIP. The algorithm then picks some variable x restricted to be integer, but whose value in the LP relaxation is fractional. Suppose its value in the LP relaxation is x = 0.7. It then excludes this value by imposing the restrictions x ≤ 0 and x ≥ 1, thereby creating two new MIPs. By applying this recursively step and exploring each resulting bifurcation, the globally optimal solution satisfying all constraints can be found.

\documentclass{standalone}

\usepackage{forest}

\tikzset{
  font=\normalsize,
  tree node/.style = {align=center, inner sep=0pt, draw, circle, minimum size=18},
  tree node label/.style={font=\scriptsize},
}

\forestset{
  declare toks={left branch prefix}{},
  declare toks={right branch prefix}{},
  declare toks={left branch suffix}{},
  declare toks={right branch suffix}{},
  maths branch labels/.style={
    branch label/.style={
      if n=1{
        edge label={node [left, midway] {$\forestoption{left branch prefix}##1\forestoption{left branch suffix}$}},
      }{
        edge label={node [right, midway] {$\forestoption{right branch prefix}##1\forestoption{right branch suffix}$}},
      }
    },
  },
  set branch labels/.style n args=4{%
    left branch prefix={#1},
    left branch suffix={#2},
    right branch prefix={#3},
    right branch suffix={#4},
  },
  branch and bound/.style={
    /tikz/every label/.append style=tree node label,
    maths branch labels,
    for tree={
      tree node,
      math content,
      s sep'+=20mm,
      l sep'+=5mm,
      thick,
      edge+={thick},
    },
    before typesetting nodes={
      for tree={
        split option={content}{:}{content,branch label},
      },
    },
  },
}

\begin{document}
\begin{forest}
  branch and bound,
  where level=1{
  set branch labels={x_1\leq}{}{x_1\geq}{},
  }{if level=2{set branch labels={x_2\leq}{}{x_2\geq}{}}{set branch labels={x_3\leq}{}{x_3\geq}{}}}
  [P_0[P_1:0][P_2:1[P_3:0[P_5:0][P_6:1]][P_4:1]]]
\end{forest}
\end{document}