Convolution Operator

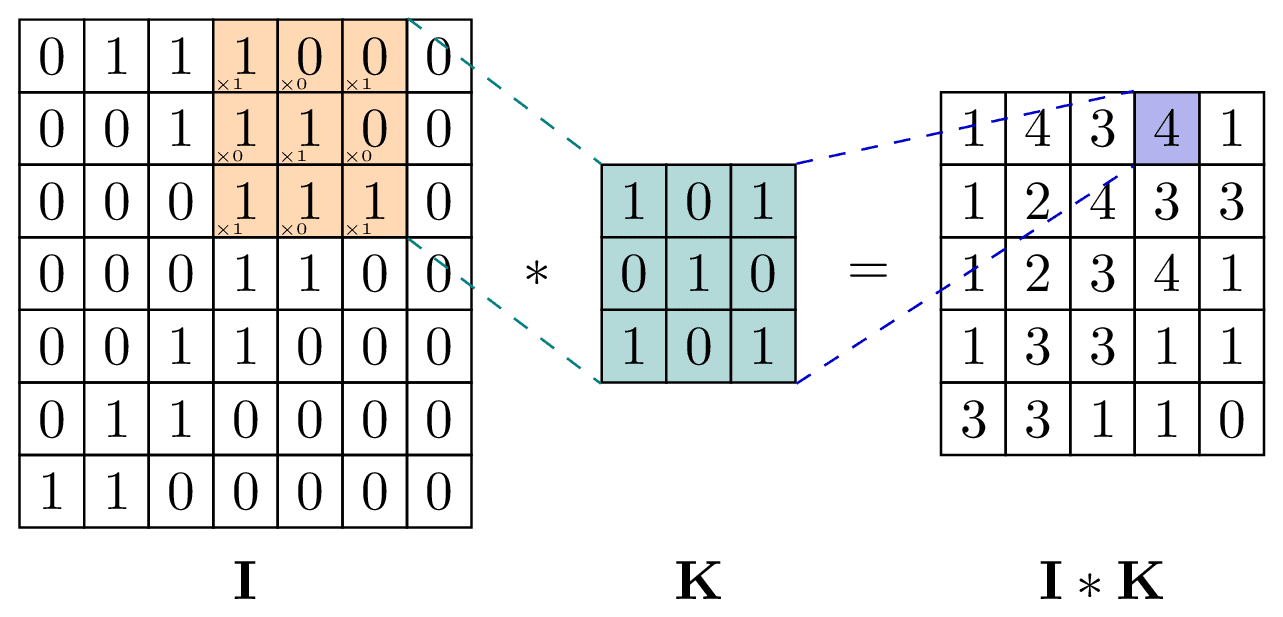
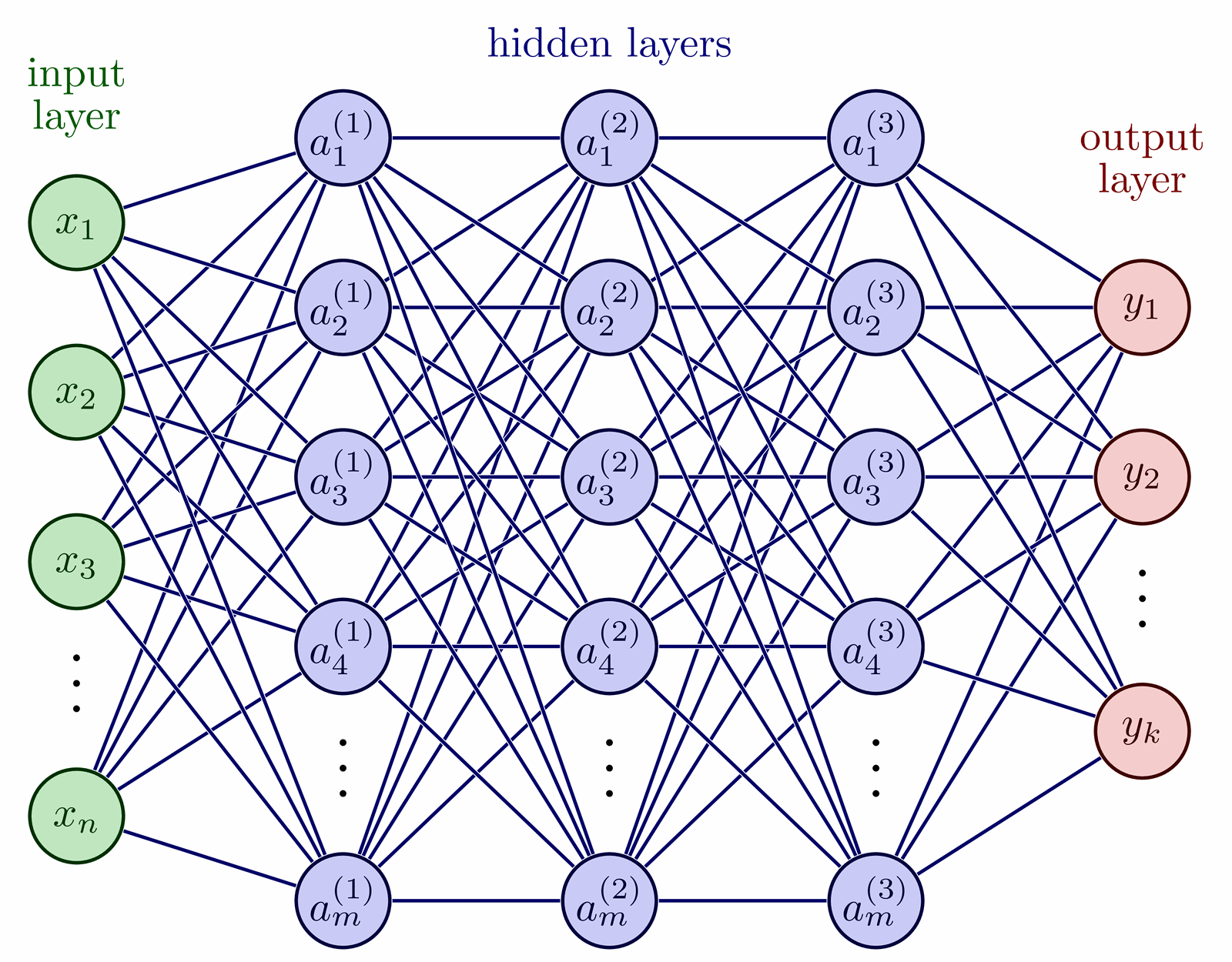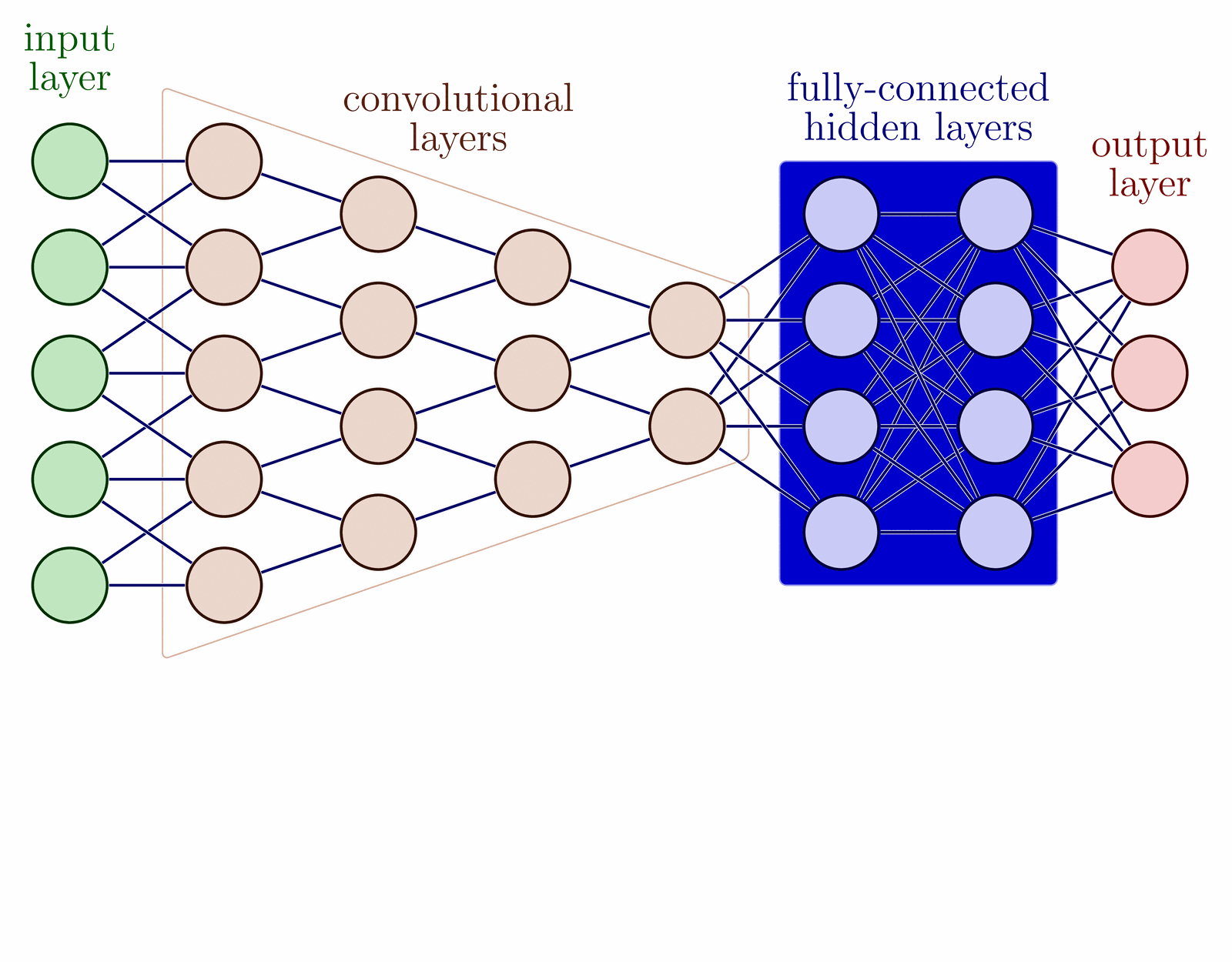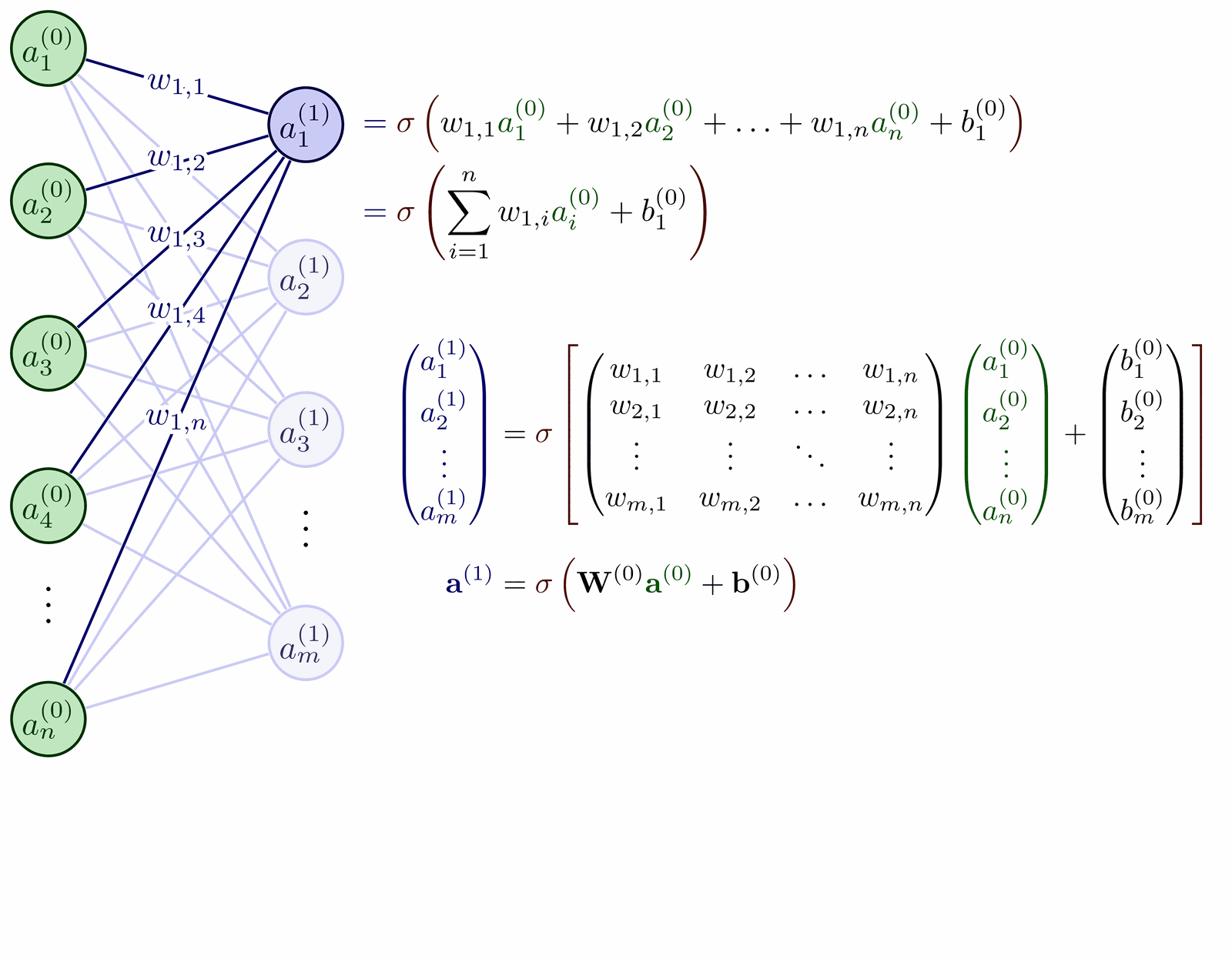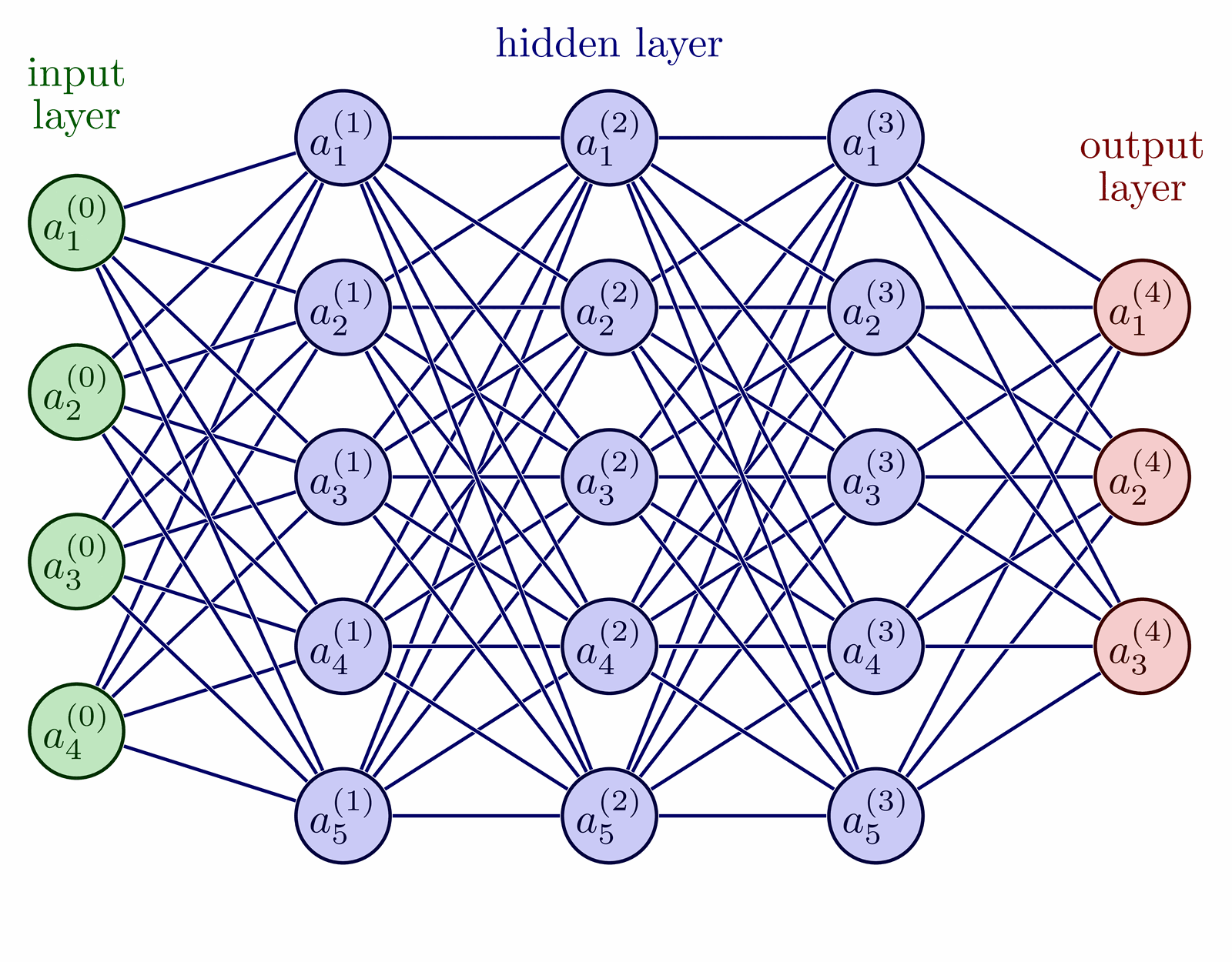
Simple 2d example illustrating the role of the Jacobian determinant in the change of variables formula. Inspired by Ari Seff in https://youtu.be/i7LjDvsLWCg?t=250.

Edit and compile if you like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
% Convolution operator.
% Adapted from https://github.com/PetarV-/TikZ/tree/master/2D%20Convolution
\documentclass[tikz]{standalone}
\usetikzlibrary{matrix, positioning}
\begin{document}
\begin{tikzpicture}[
    2d-arr/.style={matrix of nodes, row sep=-\pgflinewidth, column sep=-\pgflinewidth, nodes={draw}}
  ]
  \matrix (mtr) [2d-arr] {
  0 & 1 & 1 & |[fill=orange!30]| 1 & |[fill=orange!30]| 0 & |[fill=orange!30]| 0 & 0\\
  0 & 0 & 1 & |[fill=orange!30]| 1 & |[fill=orange!30]| 1 & |[fill=orange!30]| 0 & 0\\
  0 & 0 & 0 & |[fill=orange!30]| 1 & |[fill=orange!30]| 1 & |[fill=orange!30]| 1 & 0\\
  0 & 0 & 0 & 1 & 1 & 0 & 0\\
  0 & 0 & 1 & 1 & 0 & 0 & 0\\
  0 & 1 & 1 & 0 & 0 & 0 & 0\\
  1 & 1 & 0 & 0 & 0 & 0 & 0\\
  };
  \node[below=of mtr-5-4] {$\mathbf I$};
  \node[right=0.2em of mtr] (str) {$*$};
  \matrix (K) [2d-arr, right=0.2em of str, nodes={draw, fill=teal!30}] {
    1 & 0 & 1 \\
    0 & 1 & 0 \\
    1 & 0 & 1 \\
  };
  \node[below=of K-3-2] {$\mathbf K$};
  \node[right=0.2em of K] (eq) {$=$};
  \matrix (ret) [2d-arr, right=0.2em of eq] {
  1 & 4 & 3 & |[fill=blue!80!black!30]| 4 & 1\\
  1 & 2 & 4 & 3 & 3\\
  1 & 2 & 3 & 4 & 1\\
  1 & 3 & 3 & 1 & 1\\
  3 & 3 & 1 & 1 & 0\\
 
 
הההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההה
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX