Differential of Volume Cylindrical Coordinates

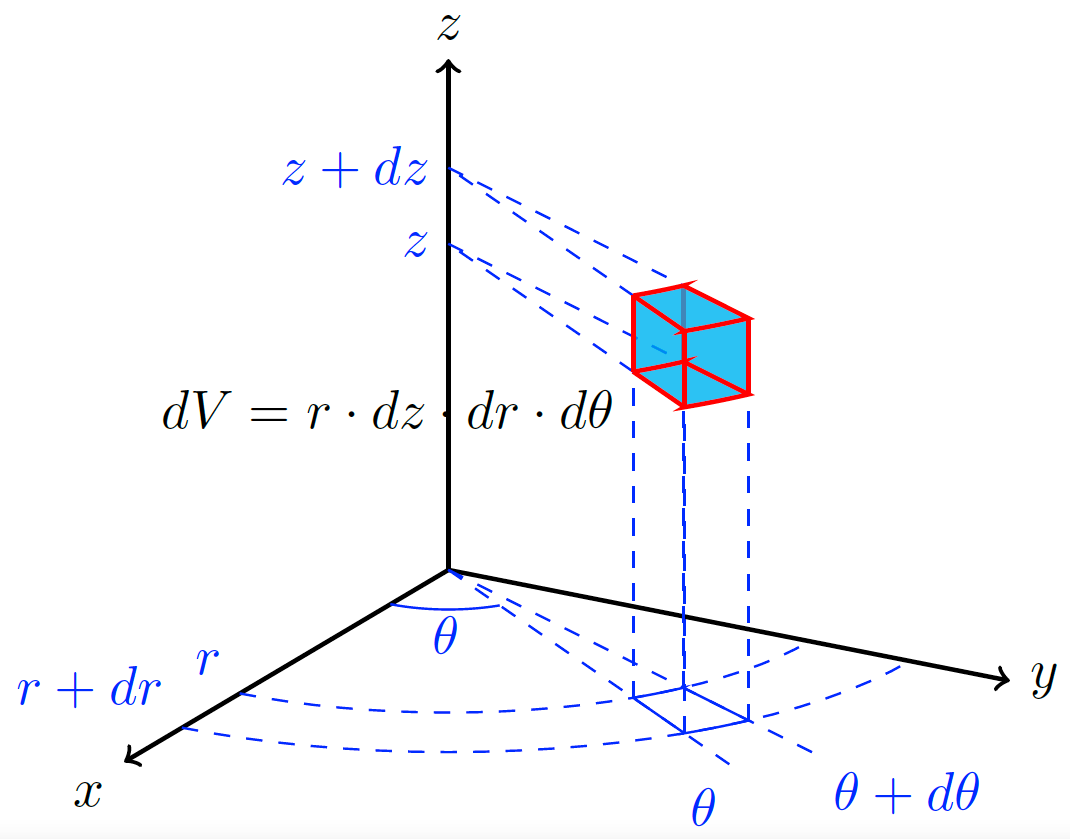
Edit and compile if you like:

\documentclass{article}
\usepackage{tikz}
\usepackage{amsmath,amssymb,amsfonts}
\usepackage{tikz-3dplot}
\usetikzlibrary{math}
\usepackage{ifthen}
\usepackage[active,tightpage]{preview}
\PreviewEnvironment{tikzpicture}
\setlength\PreviewBorder{1pt}
%
% File name: differential-of-volume-cylindrical-coordinates.tex
% Description: 
% A geometric representation of the differential of volume 
% in cylindrical coordinates is shown.
% 
% Date of creation: May, 29th, 2021.
% Date of last modification: October, 9th, 2022.
% Author: Efraín Soto Apolinar.
% https://www.aprendematematicas.org.mx/author/efrain-soto-apolinar/instructing-courses/
% Source: page 121 of the 
% Glosario Ilustrado de Matem\'aticas Escolares.
% https://tinyurl.com/5udm2ufy
%
% Terms of use:
% According to TikZ.net
% https://creativecommons.org/licenses/by-nc-sa/4.0/
% Your commitment to the terms of use is greatly appreciated.
%
\begin{document}
%
\begin{center}
\tdplotsetmaincoords{70}{120}
%
\begin{tikzpicture}[tdplot_main_coords,scale=1.5]
	% Coordinates of the location of the differential of volume
	\pgfmathsetmacro{\x}{1}
	\pgfmathsetmacro{\y}{1.5}
	\pgfmathsetmacro{\z}{1.5}
	% compute the coordinates in cylindrical coordinates
	\pgfmathsetmacro{\radio}{sqrt(\x*\x+\y*\y)}
	\pgfmathsetmacro{\angulo}{atan(\y/\x)}
	\pgfmathsetmacro{\dominio}{\angulo*pi/180}
	% For the differential
	\pgfmathsetmacro{\dradio}{0.5}
	\pgfmathsetmacro{\dangulo}{8}
	\pgfmathsetmacro{\dz}{0.35}
	\pgfmathsetmacro{\dominiof}{(\angulo+\dangulo)*pi/180}
	% Coordinates of the vertices of the differential of volume
	\pgfmathsetmacro{\Ax}{\radio*cos(\angulo)}
	\pgfmathsetmacro{\Ay}{\radio*sin(\angulo)}
	\pgfmathsetmacro{\Bx}{(\radio+\dradio)*cos(\angulo)}
	\pgfmathsetmacro{\By}{(\radio+\dradio)*sin(\angulo)}
	\pgfmathsetmacro{\Cx}{(\radio+\dradio)*cos(\angulo+\dangulo)}
	\pgfmathsetmacro{\Cy}{(\radio+\dradio)*sin(\angulo+\dangulo)}
	\pgfmathsetmacro{\Dx}{(\radio)*cos(\angulo+\dangulo)}
	\pgfmathsetmacro{\Dy}{(\radio)*sin(\angulo+\dangulo)}
	% \z = \z, it does not require conversion
	% Location of the node
	\pgfmathsetmacro{\xnodo}{0.35*cos(0.5*\angulo)}
	\pgfmathsetmacro{\ynodo}{0.35*sin(0.5*\angulo)}
	% 
	\pgfmathsetmacro{\radiof}{\radio+\dradio}
	\pgfmathsetmacro{\angulof}{\angulo+\dangulo}
	\pgfmathsetmacro{\zf}{\z+\dz}
	\pgfmathsetmacro{\xfrayouno}{(\radiof+0.5)*cos(\angulo)}
	\pgfmathsetmacro{\yfrayouno}{(\radiof+0.5)*sin(\angulo)}
	\pgfmathsetmacro{\xfrayodos}{(\radiof+0.5)*cos(\angulof)}
	\pgfmathsetmacro{\yfrayodos}{(\radiof+0.5)*sin(\angulof)}
	% Coordinate axis
	\draw[thick,->] (0,0,0) -- (\radiof+0.5,0,0) node [below left] {$x$};
	\draw[thick,->] (0,0,0) -- (0,\radiof+0.5,0) node [right] {$y$};
	\draw[thick,->] (0,0,0) -- (0,0,\zf+0.5) node [above] {$z$};
	% The origin
	\coordinate (O) at (0,0,0);
	% Differential of area in polar coordinates (in the xy plane)
	% Differential of $\theta$
	\draw[blue,dashed](0,0,0) --  (\xfrayouno,\yfrayouno,0) node[below left] {$\theta$};	
	\draw[blue,dashed](0,0,0) --  (\xfrayodos,\yfrayodos,0) node [below right] {$\theta + d\theta$};	
	% Differential of $r$ ($dr$)
	\draw[blue,dashed] plot[domain=0:0.5*pi,variable=\t] ({\radio*cos(\t r)},{\radio*sin(\t r)},0.0);
	\draw[blue,dashed] plot[domain=0:0.5*pi,variable=\t] ({\radiof*cos(\t r)},{\radiof*sin(\t r)},0.0);
	% Differential of area
	\draw[blue] (\Ax,\Ay,0) -- (\Bx,\By,0) 
					-- plot[domain=\dominio:\dominiof,variable=\t] ({\radiof*cos(\t r)},{\radiof*sin(\t r)},0.0)
					-- (\Dx,\Dy,0) 
					-- plot[domain=\dominiof:\dominio,smooth,variable=\t] ({\radio*cos(\t r)},{\radio*sin(\t r)},0.0)
					-- (\Ax,\Ay,0);
	\node[blue,above left] at (\radio,0,0) {$r$};
	\node[blue,above left] at (\radiof,0,0) {$r + dr$};
	% Auxiliary lines
	\draw[blue,dashed] (\x,\y,\z) -- (0,0,\z) node [left] {$z$};
	\draw[blue,dashed] (0,0,\z) -- (\Dx,\Dy,\z);
	\draw[blue,dashed] (\x,\y,\zf) -- (0,0,\zf) node [left] {$z + dz$};
	\draw[blue,dashed] (0,0,\zf) -- (\Dx,\Dy,\zf);
	%
	\draw[blue,dashed] (\x,\y,0) -- (\x,\y,\z);
	\draw[blue,dashed] (\Bx,\By,0) -- (\Bx,\By,\z);
	\draw[blue,dashed] (\Cx,\Cy,0) -- (\Cx,\Cy,\z);
	\draw[blue,dashed] (\Dx,\Dy,0) -- (\Dx,\Dy,\z);
	%
	\draw[blue] plot[domain=0:\dominio,smooth,variable=\t] ({0.5*cos(\t r)},{0.5*sin(\t r)});  % 0.5236
	\node[blue,below] at (\xnodo,\ynodo,0) {$\theta$};
	\node[below left] at (\Ax,\Ay,\z) {$dV = r\cdot dz \cdot dr \cdot d\theta$};
	% Differential of volume in cylindrical coordinates:
	% vertical edges
	\draw[red,thick] (\Dx,\Dy,\z) -- (\Dx,\Dy,\zf);	
	% filling in yellow to give the sensation of a solid
	% frontal face
	\fill[cyan,opacity=0.75] (\Ax,\Ay,\z) -- (\Bx,\By,\z) -- (\Bx,\By,\zf) -- (\Ax,\Ay,\zf) -- (\Ax,\Ay,\z);
	% top face
	\fill[cyan,opacity=0.75] (\Ax,\Ay,\zf) -- (\Bx,\By,\zf) 
					-- plot[domain=\dominio:\dominiof,variable=\t] ({\radiof*cos(\t r)},{\radiof*sin(\t r)},\zf)
					-- (\Dx,\Dy,\zf) 
					-- plot[domain=\dominiof:\dominio,smooth,variable=\t] ({\radio*cos(\t r)},{\radio*sin(\t r)},\zf)
					-- (\Ax,\Ay,\zf);
	% face at r + dr
	\fill[cyan,opacity=0.75] (\Bx,\By,\z) 
					-- plot[domain=\dominio:\dominiof,variable=\t] ({\radiof*cos(\t r)},{\radiof*sin(\t r)},\z) 
					-- (\Cx,\Cy,\zf) 
					-- plot[domain=\dominiof:\dominio,variable=\t] ({\radiof*cos(\t r)},{\radiof*sin(\t r)},\zf) 
					-- (\Bx,\By,\z); 
	
	% The differential of area at height $z$
	\draw[red,thick] (\Ax,\Ay,\z) -- (\Bx,\By,\z) 
					-- plot[domain=\dominio:\dominiof,variable=\t] ({\radiof*cos(\t r)},{\radiof*sin(\t r)},\z)
					-- (\Dx,\Dy,\z) 
					-- plot[domain=\dominiof:\dominio,smooth,variable=\t] ({\radio*cos(\t r)},{\radio*sin(\t r)},\z)
					-- (\Ax,\Ay,\z);
	% The differential of area at height  $z + dz$
	\draw[red,thick] (\Ax,\Ay,\zf) -- (\Bx,\By,\zf) 
					-- plot[domain=\dominio:\dominiof,variable=\t] ({\radiof*cos(\t r)},{\radiof*sin(\t r)},\zf)
					-- (\Dx,\Dy,\zf) 
					-- plot[domain=\dominiof:\dominio,smooth,variable=\t] ({\radio*cos(\t r)},{\radio*sin(\t r)},\zf)
					-- (\Ax,\Ay,\zf);
	% Vertical edges of the differential of volume
	\draw[red,thick] (\Ax,\Ay,\z) -- (\Ax,\Ay,\zf);
	\draw[red,thick] (\Bx,\By,\z) -- (\Bx,\By,\zf);
	\draw[red,thick] (\Cx,\Cy,\z) -- (\Cx,\Cy,\zf);
					
\end{tikzpicture}
\end{center}
%
\end{document}