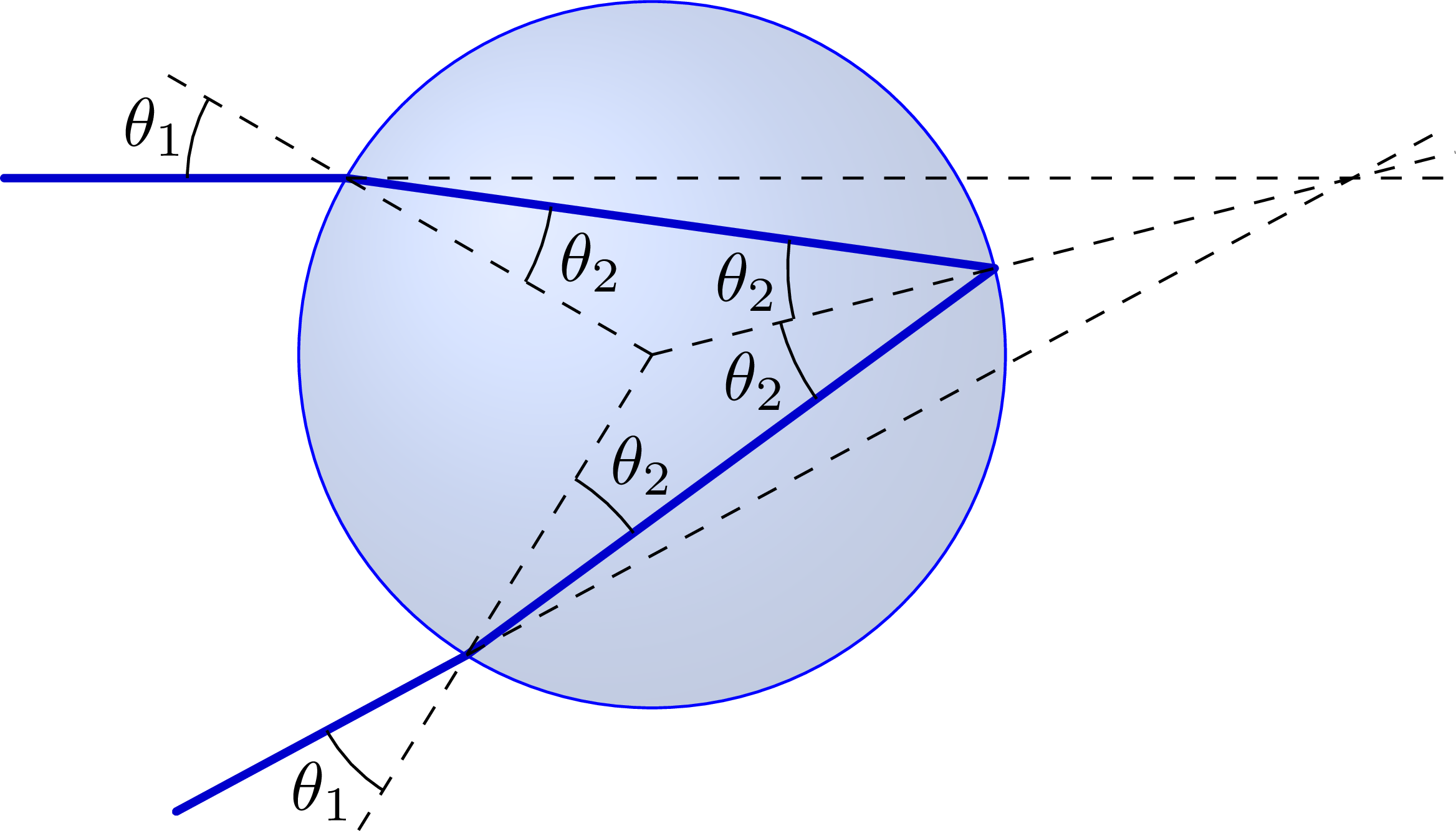
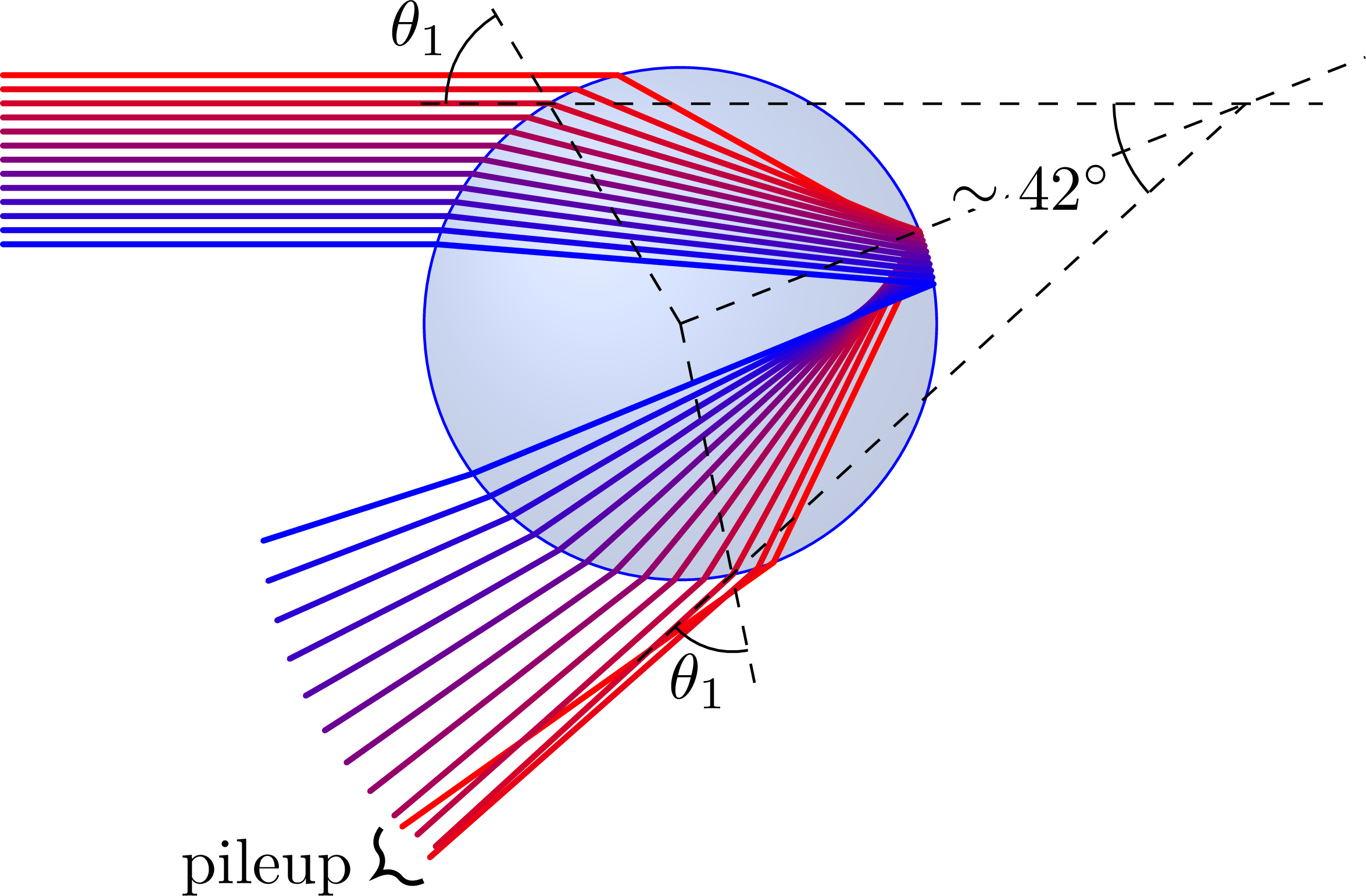
Explaining rainbows with refraction and internal reflection, including pileup at angle 42°.
Edit and compile if you like:
% Author: Izaak Neutelings (June 2020)
% Inspiration:
% https://www.researchgate.net/figure/a-Refractive-index-and-b-dispersion-of-bulky-soft-glasses-NC21-LLF1-SF6-and-F2-As_fig1_236110630
% https://link.springer.com/article/10.1007/s11082-014-9979-y
\documentclass[border=3pt,tikz]{standalone}
\usepackage{siunitx}
\usepackage[outline]{contour} % glow around text
\usetikzlibrary{calc}
\usetikzlibrary{intersections}
\usetikzlibrary{decorations.markings}
\usetikzlibrary{fadings}
\usetikzlibrary{angles,quotes} % for pic (angle labels)
\usetikzlibrary{decorations.pathreplacing} % for curly braces
\tikzset{>=latex} % for LaTeX arrow head
\contourlength{1.7pt}
\newcommand\degree{^\circ}
\colorlet{myblue}{blue!80!black}
\colorlet{myred}{black!50!red}
\colorlet{watercol}{blue!70!cyan!50}
\tikzstyle{myarr}=[-{Latex[length=3,width=2]}]
\tikzstyle{water}=[ball color=watercol]
\tikzset{
beam/.style={very thick,line cap=round,line join=round},
}
\begin{document}
% DROPLET refraction & reflection
\begin{tikzpicture}
\def\L{2.4} % length of ray outside droplet
\def\R{1.8} % droplet radius
\def\na{1.0} % air
\def\nw{1.33} % water
\def\alphI{150} % A: incident (180-90)
\pgfmathsetmacro\thetI{180-\alphI} % theta_1: incident
\pgfmathsetmacro\thetII{asin(\na/\nw*sin(\thetI)} % theta_2: air -> water & reflection
\pgfmathsetmacro\alphII{\alphI+2*\thetII-180} % C: reflected
\pgfmathsetmacro\alphIII{\alphI+4*\thetII-360} % D: exiting
\pgfmathsetmacro\py{\R*sin(\alphI)/sin(\alphII)} % intersection height
\coordinate (O) at (0,0);
\coordinate (A) at (-\L-0.5*\R,{\R*sin(\alphI)}); % incident ray
\coordinate (B) at (\alphI:\R); % entry of incident
\coordinate (C) at (\alphII:\R); % internal reflection
\coordinate (D) at (\alphIII:\R); % exit of ray
\coordinate (E) at ($(D)+(\alphIII-\thetI:0.7*\L)$); % final ray to observer
\coordinate (P) at (\alphII:\py); % intersection point
% WATER DROPLET
\fill[water] (O) circle (\R);
\fill[watercol!20,opacity=0.8] (O) circle (\R);
\draw[blue] (O) circle (\R);
% LIGHT BEAM
\draw[beam,myblue] (A) -- (B) -- (C) -- (D) -- (E);
\draw[dashed] (B) -- (P) --++ (0:0.3*\R);
\draw[dashed] (O) -- (P) --++ (\alphII:0.3*\R);
\draw[dashed] (D) -- (P) --++ (2*\alphII:0.3*\R);
\draw[dashed] (O) -- (B) --++ (\alphI:0.6*\R) coordinate (PB);
\draw[dashed] (O) -- (D) --++ (\alphIII:0.6*\R) coordinate (PD);
% ANGLES
\draw pic[-,"$\theta_1$",draw=black,angle radius=23,angle eccentricity=1.25] {angle = PB--B--A};
\draw pic[-,"$\theta_2$",draw=black,angle radius=30,angle eccentricity=1.25] {angle = O--B--C};
\draw pic[-,"$\theta_2$",draw=black,angle radius=30,angle eccentricity=1.20] {angle = B--C--O};
\draw pic[-,"$\theta_2$",draw=black,angle radius=32,angle eccentricity=1.20] {angle = O--C--D};
\draw pic[-,"$\theta_2$",draw=black,angle radius=30,angle eccentricity=1.25] {angle = C--D--O};
\draw pic[-,"$\theta_1$",draw=black,angle radius=23,angle eccentricity=1.25] {angle = E--D--PD};
\end{tikzpicture}
% DROPLET pileup
\begin{tikzpicture}
\def\L{3} % length of ray outside droplet
\def\R{1.4} % droplet radius
\def\na{1.0} % air
\def\nw{1.33} % water
\def\N{12} % number of rays
\coordinate (O) at (0,0);
% WATER DROPLET
\fill[water] (O) circle (\R);
\fill[watercol!20,opacity=0.8] (O) circle (\R);
\draw[blue] (O) circle (\R);
% LIGHT RAYS
\foreach \i [evaluate={
\y=(0.97-\i*0.66/\N)*\R; % impact parameter
\alphI=90+acos(\y/\R); % A: incident (180-90)
\thetI=180-\alphI; % theta_1: incident
\thetII=asin(\na/\nw*sin(\thetI); % theta_2: air -> water & reflection
\alphII=\alphI+2*\thetII-180; % C: reflected
\alphIII=\alphI+4*\thetII-360; % D: exiting
\f=100-\i*100/\N; % color fraction
\s=0.8-0.4*\i/\N+0.03*int(\y>0.9*\R); % scale
}] in {0,...,\N}{
\coordinate (A) at (-\L-0.5*\R,\y); % incident ray
\coordinate (B) at (\alphI:\R); % entry of incident
\coordinate (C) at (\alphII:\R); % internal reflection
\coordinate (D) at (\alphIII:\R); % exit of ray
\coordinate (E\i) at ($(D)+(\alphIII-\thetI:\s*\L)$); % final ray to observer
\draw[beam,red!\f!blue,line width=0.9]
(A) -- (B) -- (C) -- (D) -- (E\i);
}
% PILEUP
% https://en.wikipedia.org/wiki/Rainbow#Mathematical_derivation
% beta = alpI - alpII = 180-2*40.2 = 99.6
\def\bet{99.6} % alpI - alpII
\pgfmathsetmacro\thetII{90-\bet/2} % theta_2: air -> water & reflection
\pgfmathsetmacro\thetI{asin(\nw/\na*sin(\thetII)} % theta_1: incident
\pgfmathsetmacro\alphI{180-\thetI} % A: incident (180-90)
\pgfmathsetmacro\alphII{\alphI+2*\thetII-180} % C: reflected
\pgfmathsetmacro\alphIII{\alphI+4*\thetII-360} % D: exiting
\pgfmathsetmacro\py{\R*sin(\alphI)/sin(\alphII)} % intersection height
\coordinate (A) at (-\L-\R,{\R*sin(\alphI)}); % incident ray
\coordinate (B) at (\alphI:\R); % entry of incident
\coordinate (C) at (\alphII:\R); % internal reflection
\coordinate (D) at (\alphIII:\R); % exit of ray
\coordinate (E) at ($(D)+(\alphIII-\thetI:0.5*\R)$); % final ray to observer
\coordinate (P) at (\alphII:\py); % intersection point
\draw[dashed] (B)++(180:0.5*\R) -- (P) --++ (0:0.3*\R);
\draw[dashed] (E) -- (D) -- (P); %--++ (0:0.3*\R)
\draw[dashed] (O) -- (P) --++ (\alphII:0.5*\R);
\draw[dashed] (O) -- (B) --++ (\alphI:0.5*\R) coordinate (PB);
\draw[dashed] (O) -- (D) --++ (\alphIII:0.5*\R) coordinate (PD);
% ANGLES
\draw pic["\strut$\theta_1$",draw=black,angle radius=16,angle eccentricity=1.45] {angle = PB--B--A};
\draw pic["$\theta_1$",draw=black,angle radius=12,angle eccentricity=1.45] {angle = E--D--PD};
\draw pic["\contour{white}{$\sim42\degree$}",draw=black,angle radius=20.5,angle eccentricity=1.75] {angle = B--P--D};
% BRACE
\draw[thick,decorate,decoration={brace,amplitude=5}]
($(E2)+(-110:0.2)$) -- ($(E3)+(170:0.2)$) node[black,midway,below=2,left=4] {pileup};
\end{tikzpicture}
% DROPLET dispersion & rainbow
\begin{tikzpicture}
\def\L{1.8} % length of ray outside droplet
\def\R{1.6} % droplet radius
\def\na{1.0} % air
\def\N{6} % number of rays
\def\alphI{100} % A: incident (180-90)
\pgfmathsetmacro\thetI{180-\alphI} % theta_1: incident
% WATER DROPLET
\fill[water] (O) circle (\R);
\fill[watercol!20,opacity=0.8] (O) circle (\R);
\draw[blue] (O) circle (\R);
% LIGHT RAYS
\coordinate (O) at (0,0);
\coordinate (A) at (-\L-\R,{\R*sin(\alphI)}); % incident ray
\foreach \i [evaluate={
\lamb=410+\i*320/\N; % wavelength (for color)
\nw=1.36-0.08*\i/\N; % refractive index of water
\thetII=asin(\na/\nw*sin(\thetI); % theta_2: air -> water & reflection
\alphII=\alphI+2*\thetII-180; % C: reflected
\alphIII=\alphI+4*\thetII-360; % D: exiting
\s=0.8+0.45*\i/\N; % scale
}] in {0,...,\N}{
\definecolor{tmpcol}{wave}{\lamb}
\colorlet{mycol}[rgb]{tmpcol}
\coordinate (B) at (\alphI:\R); % entry of incident
\coordinate (C) at (\alphII:\R); % internal reflection
\coordinate (D) at (\alphIII:\R); % exit of ray
\coordinate (E) at ($(D)+(\alphIII-\thetI:\s*\L)$); % final ray to observer
\draw[beam,thick,mycol]
(B) -- (C) -- (D) -- (E);
}
% WHITE FADE
\def\nw{1.30}
\pgfmathsetmacro\thetII{asin(\na/\nw*sin(\thetI)}
\draw[myblue,line width=1.3] (A) -- (B);
\draw[beam,white,line width=1.0] (A) -- (B);
%\draw[beam,white,line width=1.0,path fading=east] (B) --++ (-180+\alphI+\thetII:0.01);
\draw[beam,white,line width=1.0,path fading=east] (B) --++ (-180+\alphI+\thetII:0.6*\R);
%\draw[beam,white,line width=1.2] (B)++(-0.005,0) -- (B) --++ (-180+\alphI+\thetII:0.005);
\end{tikzpicture}
% GRADIENT RAINBOW
% Instead of smooth gradient, use many thin polygons
\begin{tikzpicture}
\def\H{1} % width of band
\def\L{4} % length of rays
\def\N{200}
\foreach \i [evaluate={\f=\i/\N; \lamb=410+\f*320;\y=\f*\H;}] in {0,...,\N}{
\definecolor{tmpcol}{wave}{\lamb}
\colorlet{mycol}[rgb]{tmpcol}
\draw[mycol,line width=0.3] (0,\y) -- (\L,\y);
}
\end{tikzpicture}
% GRADIENT RAINBOW - divergent
% Instead of smooth gradient, use many thin polygons
\begin{tikzpicture}
\def\H{1} % width of band
\def\L{4} % length of rays
\def\N{200}
\foreach \i [evaluate={\f=\i/\N; \lamb=410.+\f*320.;\y=\f*\H;}] in {0,...,\N}{
\definecolor{tmpcol}{wave}{\lamb}
\colorlet{mycol}[rgb]{tmpcol}
%\draw[beam,thick,mycol] (0,\y) -- (\L,\y);
\fill[mycol,line width=0.3] (0,0) -- (\L,\y+0.05) -- (\L,\y-0.05) -- cycle;
}
\end{tikzpicture}
\end{document}Click to download: optics_rainbow.tex • optics_rainbow.pdf
Open in Overleaf: optics_rainbow.tex