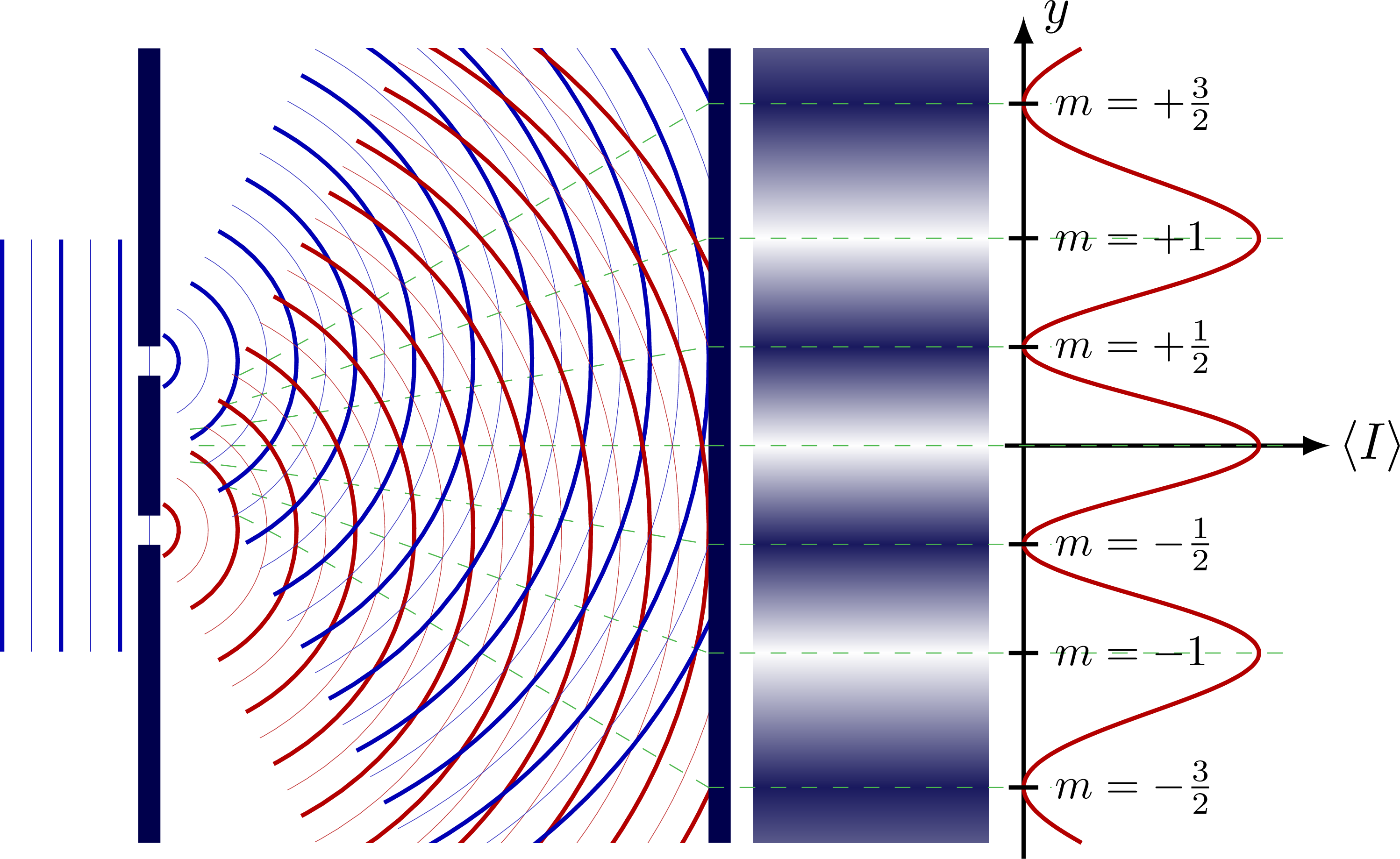
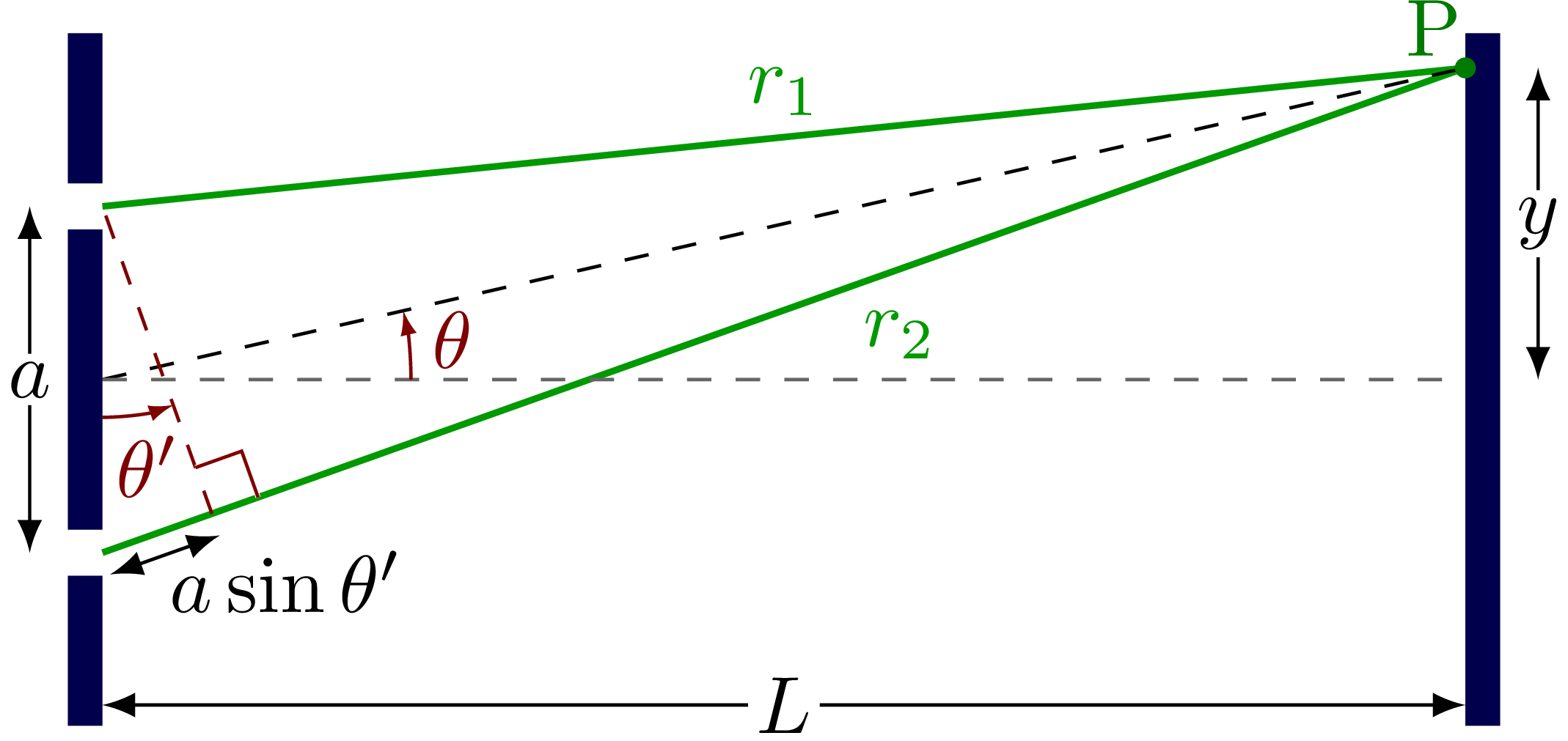
Decibel scale, with some intuitive examples.
% Author: Izaak Neutelings (June 2020)
% Inspiration:
% https://courses.physics.ucsd.edu/2011/Summer/session1/physics2c/diffraction.pdf
% https://tex.stackexchange.com/questions/201830/periodic-shading-in-tikz
\documentclass[border=3pt,tikz]{standalone}
\usepackage[outline]{contour} % glow around text
\usepackage{physics}
\usepackage{xcolor}
\usepackage{etoolbox} %ifthen
\usetikzlibrary{calc}
\usetikzlibrary{arrows,arrows.meta}
\usetikzlibrary{decorations.markings}
\usetikzlibrary{angles,quotes} % for pic (angle labels)
\usetikzlibrary{fadings}
\tikzset{>=latex} % for LaTeX arrow head
\contourlength{1.4pt}
\colorlet{wall}{blue!30!black}
\colorlet{myblue}{blue!70!black}
\colorlet{myred}{red!70!black}
\colorlet{mydarkred}{red!50!black}
\colorlet{mylightgreen}{green!60!black!70}
\colorlet{mygreen}{green!60!black}
\colorlet{myredgrey}{red!50!black!80}
\colorlet{myshadow}{blue!30!black!90}
\tikzstyle{wave}=[myblue,thick]
\tikzstyle{mydashed}=[black!70,dashed,thin]
\tikzstyle{mymeas}=[{Latex[length=3,width=2]}-{Latex[length=3,width=2]},thin]
\tikzstyle{mysmallarr}=[-{Latex[length=3,width=2]}]
\newcommand\rightAngle[4]{
\pgfmathanglebetweenpoints{\pgfpointanchor{#2}{center}}{\pgfpointanchor{#3}{center}}
\coordinate (tmpRA) at ($(#2)+(\pgfmathresult+45:#4)$);
\draw[white,line width=0.6] ($(#2)!(tmpRA)!(#1)$) -- (tmpRA) -- ($(#2)!(tmpRA)!(#3)$);
\draw[mydarkred] ($(#2)!(tmpRA)!(#1)$) -- (tmpRA) -- ($(#2)!(tmpRA)!(#3)$);
}
\newcommand\lineend[2]{
\def\w{0.1} \def\c{30}
\draw[mygreen] (#1)++(#2:\w) to[out=#2-180-\c,in=#2+\c] (#1)
to[out=#2+\c-180,in=#2-\c]++ (#2-180:\w);
}
\def\tick#1#2{\draw[thick] (#1) ++ (#2:0.1) --++ (#2-180:0.2)}
% INTERFERENCE FADING
\begin{tikzfadingfrompicture}[name=interference]
\def\lambd{0.5} % wavelength
\foreach \r in {1,...,15}
\foreach \j in {1,...,25}
\path [line width=\lambd*\j,draw=transparent!0,opacity=0.04]
(0,0) circle (\lambd*\r); %(0:\r) arc (0:180:\r);
\end{tikzfadingfrompicture}
\begin{document}
% INTERFERENCE FADING
\begin{tikzpicture}
\def\a{2} % distance sources
\def\W{8} % distance between walls
\def\H{8} % total wall height
%\clip (-\W/2,0) rectangle ++(\W,\H);
\path[fill=myshadow,path fading=interference,fit fading=false,fading transform={shift={(0,\a/2)}}] %,shift={(-2,0)}
(0,-\H/2) rectangle ++(\W,\H);
\path[fill=myshadow,path fading=interference,fit fading=false,fading transform={shift={(0,-\a/2)}}] %rotate=45
(0,-\H/2) rectangle ++(\W,\H);
%\draw (0,0) --++ (0,\H);
\end{tikzpicture}
% TWO SPLIT
\begin{tikzpicture}[
nodal/.style={mylightgreen,dashed,very thin},
declare function={
%xnode(\n,\dn,\lam,\f) = sqrt( (\n^2+(\n+\dn)^2)*\lambd^2/2 - (\n^2-(\n+\dn)^2)^2*\lambd^4/(4*\a^2) - \a^2/4 );
xnode(\n,\dn,\lam,\f) = \lam/\f*sqrt( \n^2*(\f^2-\dn^2)+\n*\dn*(\f^2-\dn^2)+\dn^2*\f^2/2-(\f^4+\dn^4)/4 );
ynode(\n,\dn,\lam,\a) = (2*\n*\dn+\dn^2)*\lam/(2*\f);
intensity(\y,\lam,\a,\L) = cos(180*\a*\y/(2*\lam*sqrt(\L*\L+\y*\y)))^2;
}
]
\def\L{3.8} % distance between walls
\def\H{5.4} % total wall height
\def\h{2.8} % plane wave height
\def\t{0.15} % wall thickness
\def\a{1.15} % slit distance
\def\d{0.20} % slit size
\def\N{21} % number of waves
\def\lambd{0.20} % wavelength
\def\R{\N*\lambd} % wave radius
\def\Nlines{3} % number of nodal lines
\def\A{1.6} % amplitude
%\def\r{0.06} % point source radius
%\def\nmax{10}
\def\nsamples{100}
\def\ang{62}
\begin{scope}
\clip (-\t/2,-\H/2) rectangle (\L,\H/2);
%\clip (-\t/2,0.7*\a) -- (0.6*\L,\H/2) -- (\L,\H/2) --
% (\L,-\H/2) -- (0.6*\L,-\H/2) -- (-\t/2,-0.7*\a) -- cycle;
% NODAL LINES
\draw[nodal]
(0.08*\N*\lambd,0) -- (1.06*\R,0);
\coordinate (NP0) at (\L,0); % to avoid "Dimension too large error"
\foreach \dn [evaluate={
\f=\a/\lambd;
\nmin=2.5+0.2*\dn; %0.501*(-\dn+\f)
\nmax=10; %(NP0)
\c=int(\dn<\f);
\y=\L/sqrt((\a/(\lambd*\dn))^2-1);
}] in {1,...,\Nlines}{
\coordinate (NP+\dn) at (\L,\y); % to avoid "Dimension too large error"
\coordinate (NP-\dn) at (\L,-\y); % to avoid "Dimension too large error"
\ifnum\c=1
\draw[nodal,variable=\n,samples=\nsamples,smooth]
plot[domain=\nmin:\nmax] ({xnode(\n,\dn,\lambd,\f)},{ynode(\n,\dn,\lambd,\f)})
-- (NP+\dn);
\draw[nodal,variable=\n,samples=\nsamples,smooth]
plot[domain=\nmin:\nmax] ({xnode(\n,\dn,\lambd,\f)},{-ynode(\n,\dn,\lambd,\f)})
-- (NP-\dn);
\fi
}
% WAVES
\foreach \i [evaluate={\R=\i*\lambd;}] in {1,...,\N}{
\ifodd\i
\draw[myblue,line width=0.8] (0,\a/2)++(\ang:\R) arc (\ang:-\ang:\R);
\draw[myred,line width=0.8] (0,-\a/2)++(\ang:\R) arc (\ang:-\ang:\R);
\else
\draw[myblue!80,line width=0.1] (0,\a/2)++(\ang:\R) arc (\ang:-\ang:\R);
\draw[myred!80,line width=0.1] (0,-\a/2)++(\ang:\R) arc (\ang:-\ang:\R);
\fi
}
\end{scope}
% PLANE WAVES
\foreach \i [evaluate={\x=-\i*\lambd;}] in {0,...,5}{
\ifodd\i
\draw[myblue,line width=0.8] (\x,-\h/2) -- (\x,\h/2);
\else
\draw[myblue,line width=0.1] (\x,-\h/2) -- (\x,\h/2);
\fi
}
% WALL
\fill[wall]
(\t/2,\a/2-\d/2) rectangle (-\t/2,-\a/2+\d/2)
(\t/2,\a/2+\d/2) rectangle (-\t/2,\H/2)
(\t/2,-\a/2-\d/2) rectangle (-\t/2,-\H/2)
(\L,-\H/2) rectangle (\L+\t,\H/2);
% SHADES
\begin{scope}[shift={(1.08*\L,0)}]
\def\yz{\L/sqrt((\a/\lambd)^2-1)} % m = +- 1/2
\def\yZ{\L/sqrt((\a/\lambd/2)^2-1)} % m = +- 1
\clip (0,-\H/2) rectangle (1.1*\A,\H/2);
\fill[white] (0,-\H/2) rectangle++ (\A,\H); % to fill seams
\foreach \i [evaluate={\n=0.5*\i;\yn=\L/sqrt((\a/(2*\lambd*\n))^2-1);
}] in {1,...,\Nlines}{
\ifodd\i % if even
\fill[myshadow] (0,{-\yn-0.1}) rectangle++ (\A,0.2); % to fill seams
\fill[myshadow] (0,{ \yn-0.1}) rectangle++ (\A,0.2); % to fill seams
\fi
}
\path[left color=myshadow,right color=myshadow,middle color=white,shading angle={180}]
(0,{-\yz}) rectangle (\A,{\yz});
\foreach \i [evaluate={
\n=0.5*\i;
\m=0.5*(\i+1);
\yn=\L/sqrt((\a/(2*\lambd*\n))^2-1);
\ym=\L/sqrt((\a/(2*\lambd*\m))^2-1);
\dang=mod(\i,2)*180;
}] in {1,...,\Nlines}{
\path[left color=myshadow,right color=white,shading angle={\dang}]
(0,\yn) rectangle (\A,\ym);
\path[left color=myshadow,right color=white,shading angle={180+\dang}]
(0,-\yn) rectangle (\A,-\ym);
}
\end{scope}
% INTENSITY
\begin{scope}[shift={(1.1*\L+1.1*\A,0)}]
\draw[->,thick] (-0.08*\A,0) -- (1.3*\A,0) node[right=-2] {$\expval{I}$}; % I axis
\draw[->,thick] (0,-0.52*\H) -- (0,0.54*\H) node[right] {$y$}; % y axis
\draw[nodal] (NP0) --++ (0.15*\L+2.1*\A,0); % green nodal lines
\foreach \i [evaluate={\y=\L/sqrt((\a/(\lambd*\i))^2-1)}] in {1,...,\Nlines}{ % green nodal lines
\draw[nodal] (NP+\i) --++ ({0.15*\L+1.1*\A+\A*intensity(\y,\lambd,\a,\L)},0);
\draw[nodal] (NP-\i) --++ ({0.15*\L+1.1*\A+\A*intensity(\y,\lambd,\a,\L)},0);
}
\draw[myred,thick,variable=\y,samples=\nsamples,smooth,domain=-\H/2:\H/2]
plot({\A*intensity(\y,\lambd,\a,\L)},\y);
\foreach \i [evaluate={ % ticks
\modd=\i; %int(\i);
\meven=int(\i-1);
\y=\L/sqrt((\a/(\lambd*\i))^2-1);
}] in {1,...,\Nlines}{
\ifodd\i
\tick{0,-\y}{180} node[right=0,scale=0.85] {$m=-\frac{\modd}{2}$};
\tick{0,\y}{180} node[right=0,scale=0.85] {$m=+\frac{\modd}{2}$};
\else
\tick{0,-\y}{180} node[right=0,scale=0.85] {$m=-\meven$};
\tick{0,\y}{180} node[right=0,scale=0.85] {$m=+\meven$};
\fi
}
\end{scope}
\end{tikzpicture}
% TWO SLIT PATH DIFFERENCE
\begin{tikzpicture}
\def\L{5.9} % distance between walls
\def\H{3.0} % total wall height
\def\f{0.9} % fractional height of projection point
\def\ang{atan((\f*\H+\a)/\L/2)} % theta
\def\t{0.15} % wall thickness
\def\a{1.5} % slit distance
\def\d{0.20} % slit size
\coordinate (T) at (0,\a/2);
\coordinate (B) at (0,-\a/2);
\coordinate (L) at (0,0);
\coordinate (R) at (\L,0);
\coordinate (P) at (\L,\f*\H/2);
\coordinate (M) at ($(B)!(T)!(P)$);
% LINES
\draw[mygreen,thick] (T) -- (P) node[midway,above=-1] {$r_1$};
\draw[mygreen,thick] (B) -- (P) node[midway,below=3,right=6] {$r_2$}; %right=6,below right=-4
\draw[dashed] (L) -- (P);
\draw[dashed,black!60] (L) -- (R);
\draw[mydarkred,dashed] (M) -- (T);
% ANGLES
\draw pic[mysmallarr,"$\theta'$",mydarkred,draw=mydarkred,angle radius=26,angle eccentricity=1.25]
{angle = B--T--M};
\draw pic[mysmallarr,"$\theta$",mydarkred,draw=mydarkred,angle radius=38,angle eccentricity=1.14]
{angle = R--L--P};
\rightAngle{T}{M}{P}{0.3}
% MEASURES
\draw[<->,black] (0,-0.47*\H) --++ (\L,0) node[midway,fill=white,inner sep=1] {$L$};
\draw[<->,black] (-2.1*\t,-\a/2) --++ (0,\a) node[midway,fill=white,inner sep=1] {$a$};
\draw[<->,black] ([shift={({\ang-90}:0.1)}]B) -- ([shift={({\ang-90}:0.1)}]M)
node[midway,above=1,below right=-3]{$a\sin\theta'$};
\draw[<->,black] ([shift={(2.1*\t,0)}]P) -- ([shift={(2.1*\t,0)}]R)
node[midway,fill=white,inner sep=1]{$y$};
% WALL
\fill[wall]
(0,\a/2-\d/2) rectangle (-\t,-\a/2+\d/2)
(0,\a/2+\d/2) rectangle (-\t,\H/2)
(0,-\a/2-\d/2) rectangle (-\t,-\H/2)
(\L,-\H/2) rectangle (\L+\t,\H/2);
\fill[mygreen!80!black] (P) circle (0.3*\t) node[right=1,above left=-2] {P};
\end{tikzpicture}
% TWO SLIT PATH DIFFERENCE close up
\begin{tikzpicture}
\def\L{5.5} % distance between walls
\def\l{3.8} % distance between walls
\def\H{3.5} % total wall height
\def\f{0.9} % fractional height of projection point
\def\t{0.15} % wall thickness
\def\a{1.6} % slit distance
\def\d{0.20} % slit size
\def\ang{27} % angle
\coordinate (T) at (0,\a/2);
\coordinate (B) at (0,-\a/2);
\coordinate (L) at (0,0);
\coordinate (R) at (\L,0);
\coordinate (I) at ({\a/2/tan(\ang)},0);
% LINES
\draw[mygreen,thick] (T) --++ (\ang:.8*\l) coordinate (PT) node[midway,below=1,above left=-2] {$r_1$};
\draw[mygreen,thick] (B) --++ (\ang:\l) coordinate (PB) node[midway,left=2,below right=-1] {$r_2$};
\draw[mydarkred,dashed] (T) -- ($(B)!(T)!(PB)$) coordinate (M);
\draw[black!60,dashed] (L) --++ (\ang:.9*\l) coordinate (PR);
%\draw[black!60,dashed] (T) --++ (.20*\L,0) coordinate (TR);
\draw[black!60,dashed] (L) --++ (.6*\L,0) coordinate (LR);
%\draw[black!60,dashed] (B) --++ (.20*\L,0) coordinate (BR);
% LINE END
\lineend{PT}{\ang+70}
\lineend{PB}{\ang+70}
% ANGLES
\draw pic[mysmallarr,"\contour{white}{$\theta$}",mydarkred,draw=mydarkred,angle radius=18.8,angle eccentricity=1.38 ]
{angle = B--T--M};
%\draw pic[->,"$\theta$",mydarkred,draw=mydarkred,angle radius=16,angle eccentricity=1.41]
% {angle = TR--T--PT};
%\draw pic[->,"$\theta$",mydarkred,draw=mydarkred,angle radius=16,angle eccentricity=1.41]
% {angle = BR--B--PB};
\draw pic[mysmallarr,"$\theta$",mydarkred,draw=mydarkred,angle radius=22,angle eccentricity=1.25]
{angle = LR--L--PR};
\draw pic[mysmallarr,"$\theta$",mydarkred,draw=mydarkred,angle radius=22,angle eccentricity=1.30]
{angle = LR--I--PB};
\rightAngle{T}{M}{PB}{0.3}
% MEASURES
\draw[<->,black] (-2.2*\t,-\a/2) --++ (0,\a) node[midway,fill=white,inner sep=1.5] {$a$};
\draw[<->,black] ([shift={({\ang-90}:0.1)}]B) -- ([shift={({\ang-90}:0.1)}]M)
node[midway,above=1,below right=-3]{$a\sin\theta$};
% WALL
\fill[wall]
(0,\a/2-\d/2) rectangle (-\t,-\a/2+\d/2)
(0,\a/2+\d/2) rectangle (-\t,\H/2)
(0,-\a/2-\d/2) rectangle (-\t,-\H/2);
\end{tikzpicture}
\end{document}
Click to download: optics_twoslit.tex • optics_twoslit.pdf
Open in Overleaf: optics_twoslit.tex