Standing waves in a open and half-closed pipes. Also see standing waves in a flute, traveling waves in air, and more related figures in the Music category.
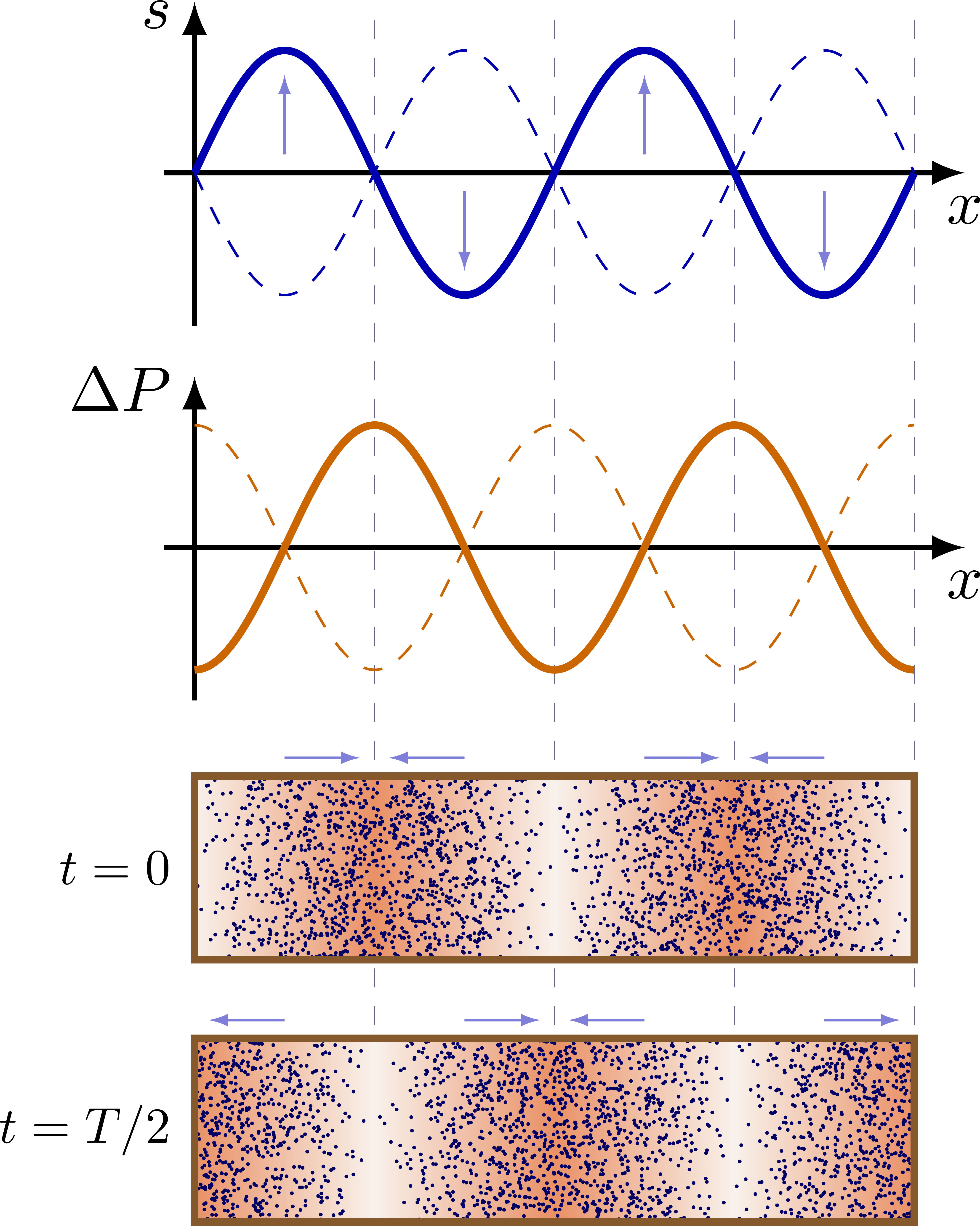
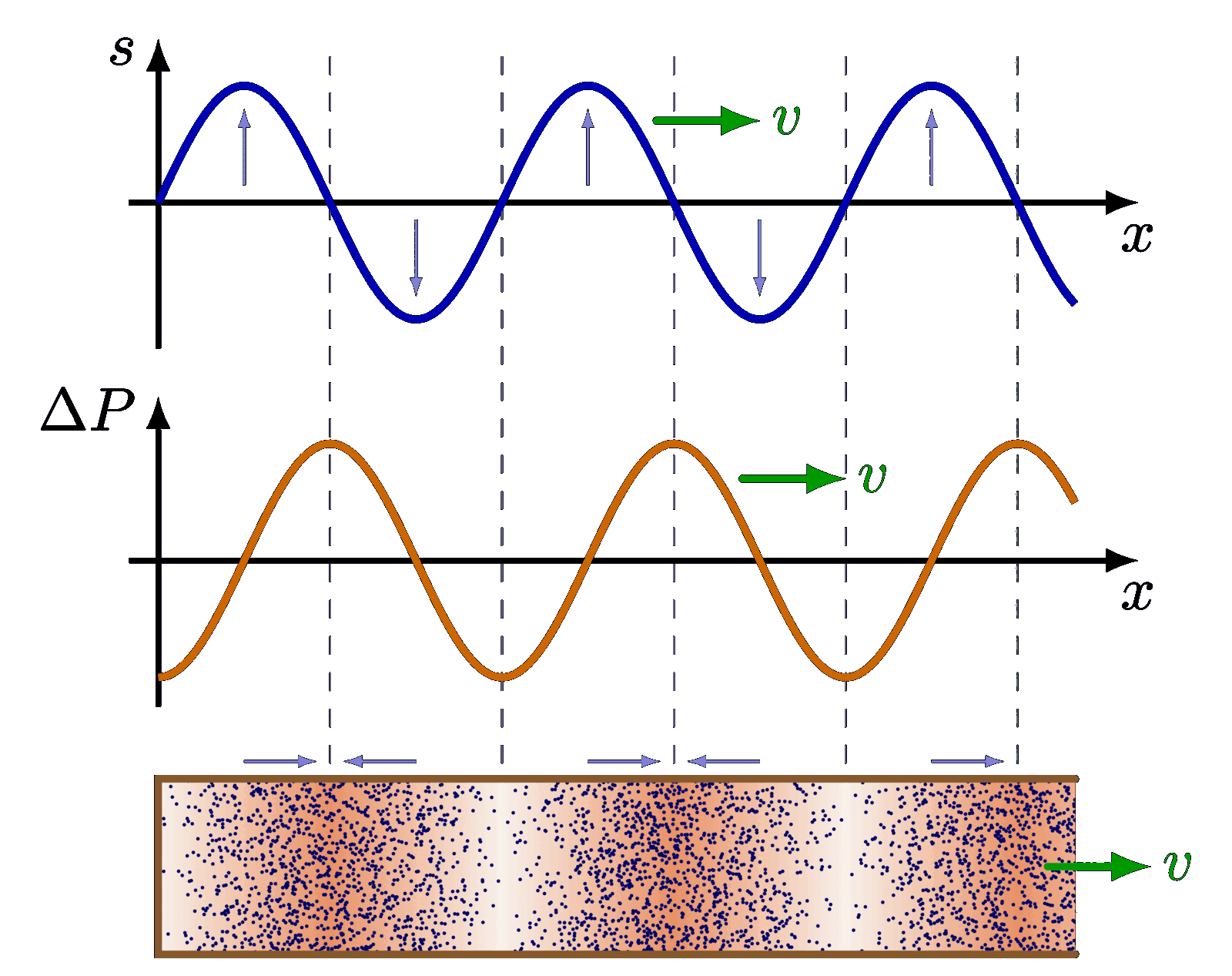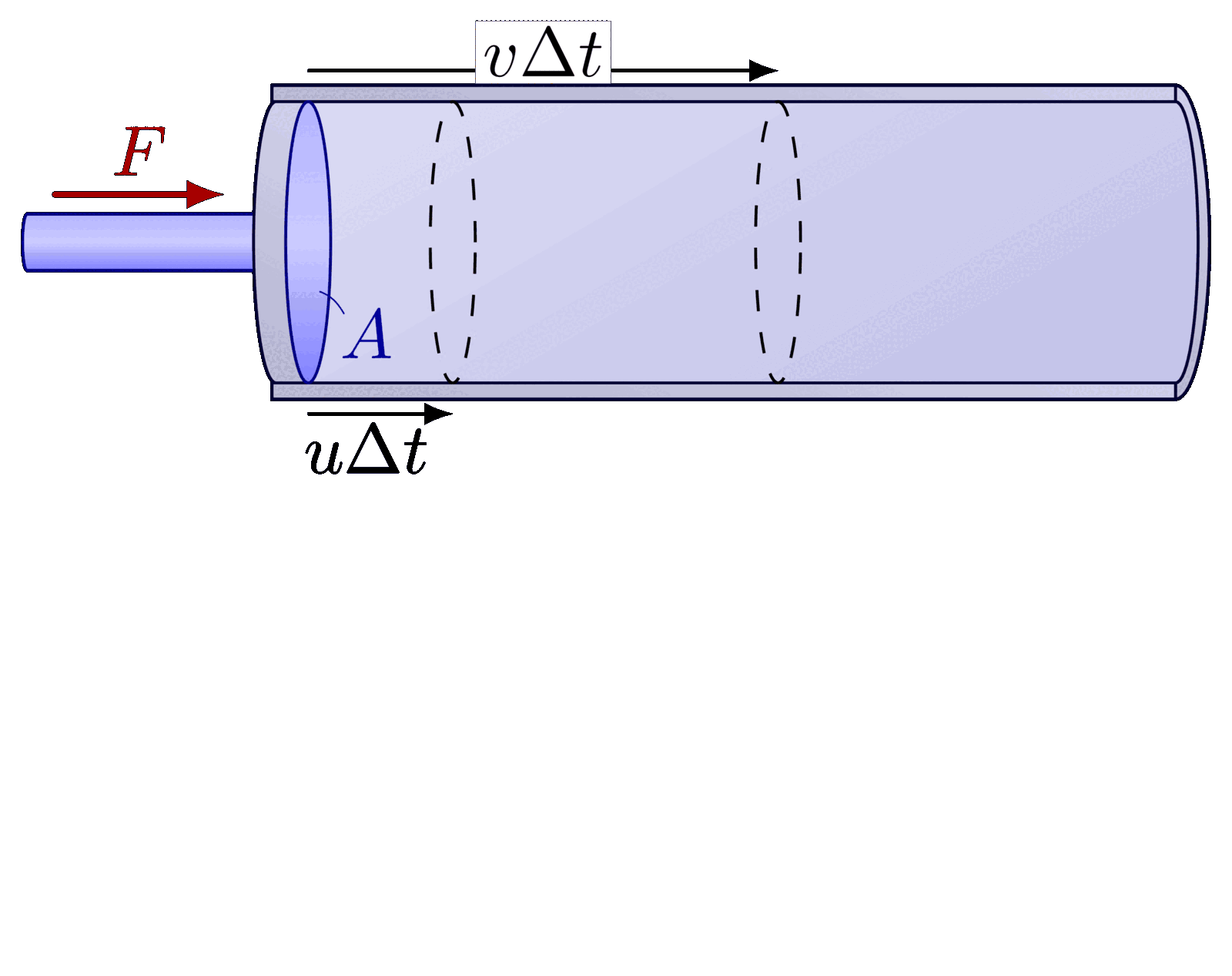
Pressure and displacement
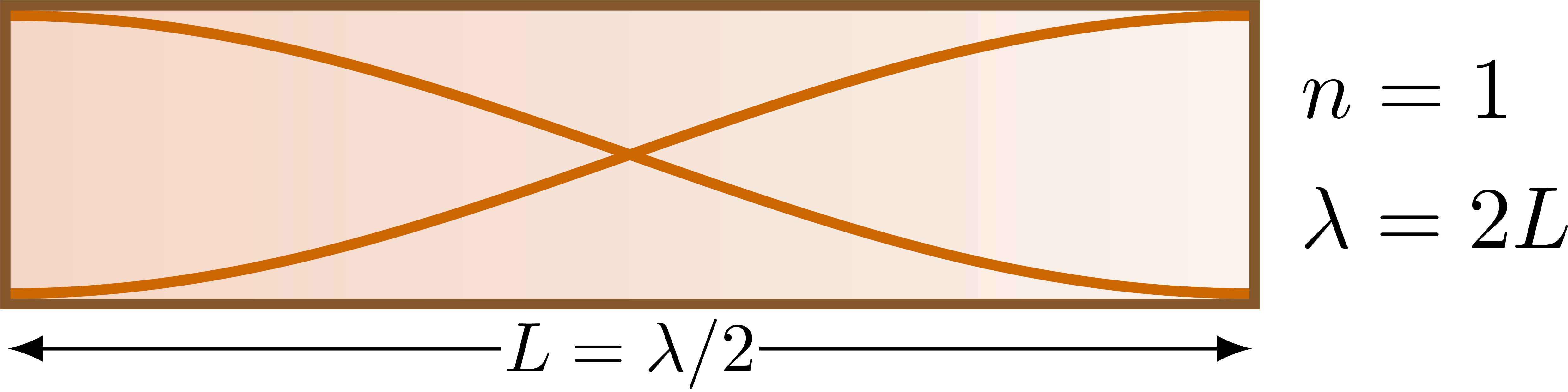
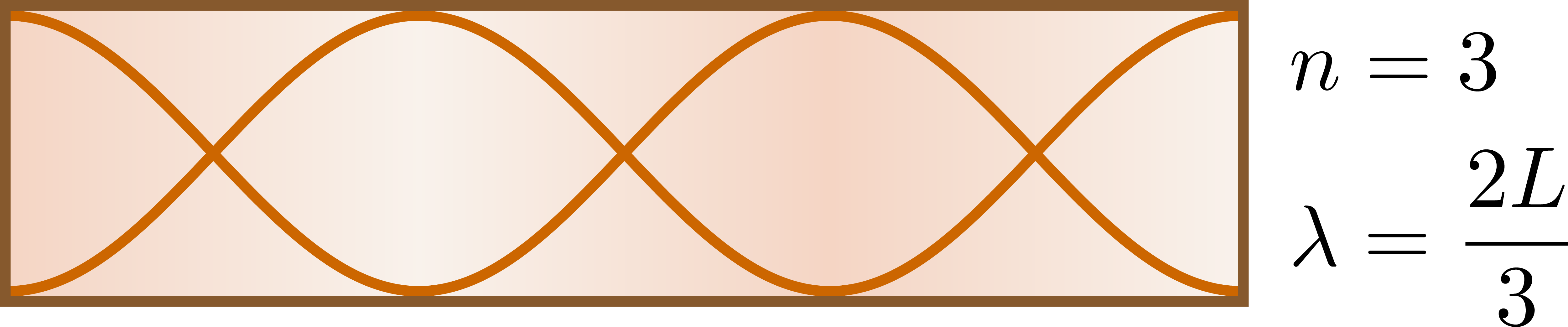
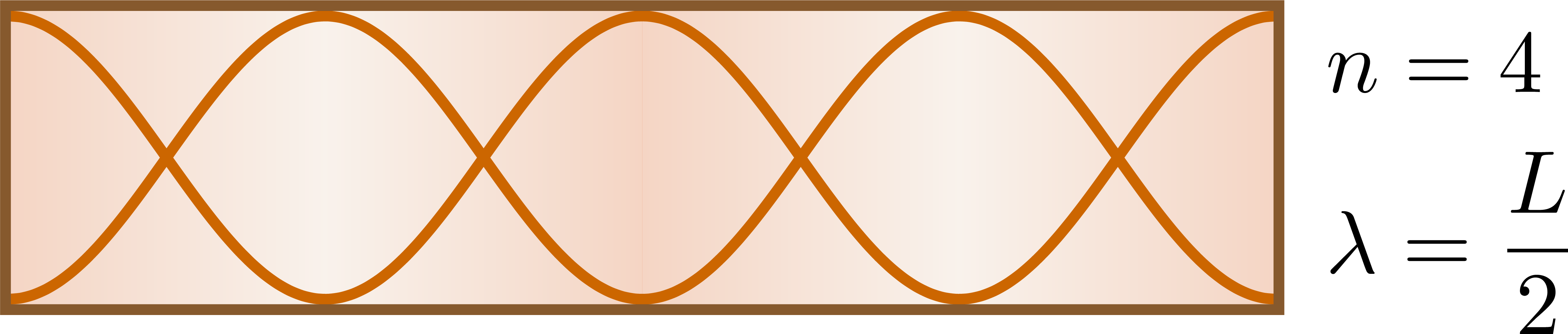
Closed pipe
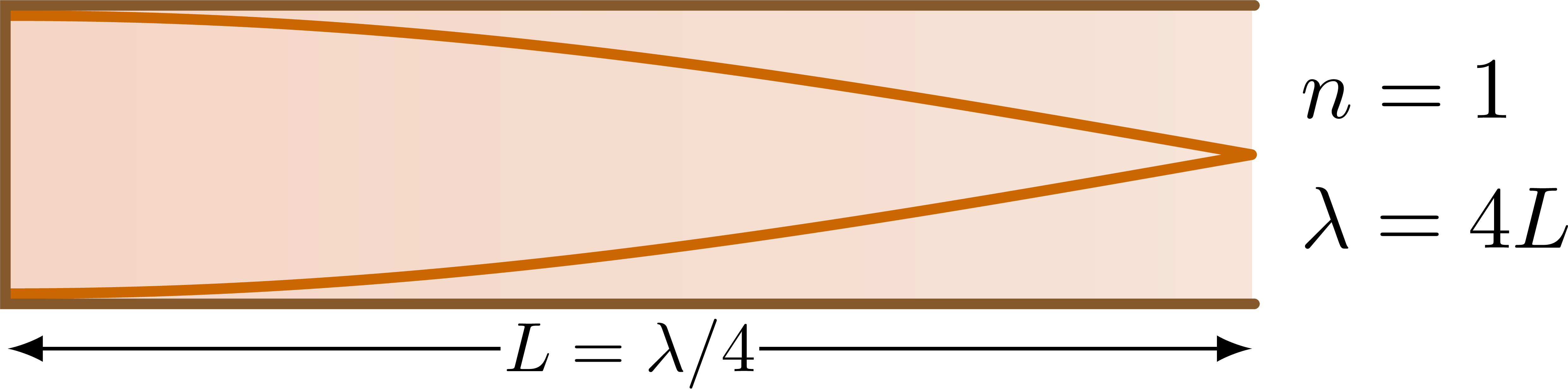
Half-open pipe
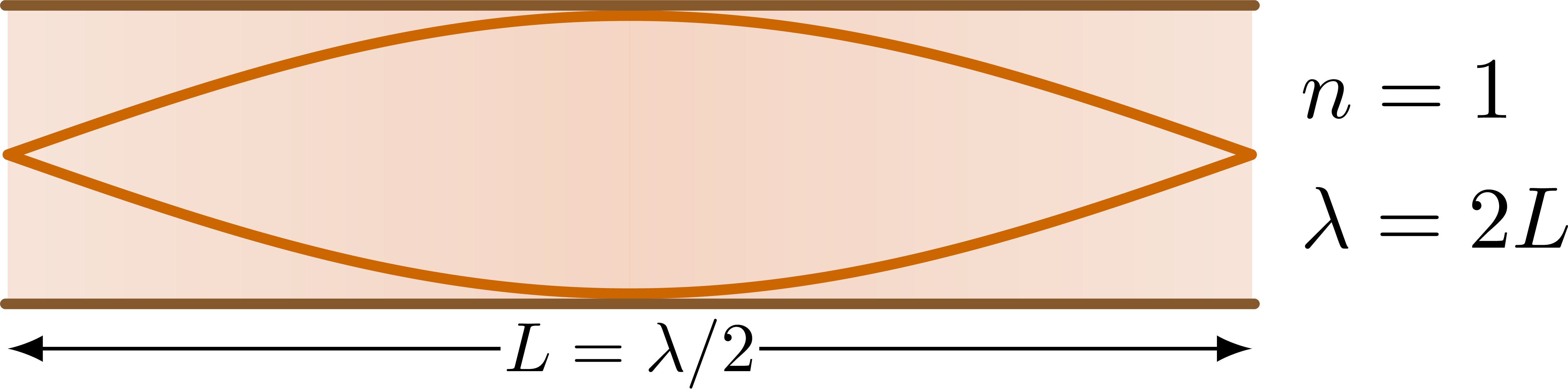
Open pipe
Edit and compile if you like:
% Author: Izaak Neutelings (December 2020)
% http://hyperphysics.phy-astr.gsu.edu/hbase/Waves/standw.html
\documentclass[border=3pt,tikz]{standalone}
\usepackage{amsmath}
\usepackage{etoolbox} % ifthen
\usepackage{tikz}
\usetikzlibrary{arrows.meta} % for arrow size
\tikzset{>=latex} % for LaTeX arrow head
\colorlet{xcol}{blue!70!black}
\colorlet{vcol}{green!60!black}
\colorlet{Pcol}{orange!80!black}
\colorlet{dense air}{Pcol!70!red!60}
\colorlet{thin air}{brown!10}
\colorlet{myred}{red!65!black}
\tikzstyle{vvec}=[->,vcol,very thick,line cap=round]
\tikzstyle{wood}=[very thick,brown!70!black]
\tikzstyle{Pline}=[Pcol,very thick,line cap=round]
\def\tick#1#2{\draw[thick] (#1) ++ (#2:0.1) --++ (#2-180:0.2)}
\tikzstyle{myarr}=[xcol!50,-{Latex[length=3,width=2]}]
\begin{document}
% STANDING WAVE
\begin{tikzpicture}
\message{Standing wave plot...^^J}
\def\lam{2.0} % wavelength
\def\n{2} % harmonic
\def\L{\n*\lam} % length
\def\ymax{0.85} % y maximum
\def\xmax{1.02*\L} % x maximum
\def\A{0.80*\ymax} % amplitude
\def\D{1.20*\ymax} % pipe diameter
\def\s{2.45*\ymax} % shift
\def\N{1200} % number of points
%\def\N{500} % number of points
% DISPLACEMENT
\foreach \i [evaluate={\x=(\i-0.75)*\lam;}] in {1,...,\n}{
\draw[myarr] (\x,0.15*\A) --++ (0,0.65*\A);
\draw[myarr] (\x+\lam/2,-0.15*\A) --++ (0,-0.65*\A);
\draw[blue!20!black!60,very thin,dashed] (\x+\lam/4,\ymax) --++ (0,-2.8*\s);
\draw[blue!20!black!60,very thin,dashed] (\x+3*\lam/4,\ymax) --++ (0,-2.8*\s);
}
\draw[->,thick] (0,-\ymax) -- (0,0.1+\ymax) node[below=2,left] {$s$};
\draw[->,thick] (-0.2*\ymax,0) -- (0.2+\xmax,0) node[below] {$x$};
\draw[xcol,very thick,samples=100,smooth,variable=\x,domain=0:\L]
plot(\x,{\A*sin(360/\lam*\x)});
\draw[xcol,dashed,samples=100,smooth,variable=\x,domain=0:\L]
plot(\x,{-\A*sin(360/\lam*\x)});
% PRESSURE
\begin{scope}[shift={(0,-\s)}]
\draw[->,thick] (0,-\ymax) -- (0,0.1+\ymax) node[below=2,left] {$\Delta P$};
\draw[->,thick] (-0.2*\ymax,0) -- (0.2+\xmax,0) node[below] {$x$};
\draw[Pcol,very thick,samples=100,smooth,variable=\x,domain=0:\L]
plot(\x,{\A*sin(360/\lam*\x-90)});
\draw[Pcol,dashed,samples=100,smooth,variable=\x,domain=0:\L]
plot(\x,{-\A*sin(360/\lam*\x-90)});
\end{scope}
% TUBE, t = 0
\message{ Generating gas particles at t = 0...^^J}
\begin{scope}[shift={(0,-2.1*\s)}]
\fill[thin air] (0,0) rectangle++ (\L,\D); % to fill seams
\foreach \i [evaluate={\x=(\i-1)*\lam;}] in {1,...,\n}{
\draw[myarr] (\x+0.25*\lam,1.1*\D) --++ ( 0.21*\lam,0);
\draw[myarr] (\x+0.75*\lam,1.1*\D) --++ (-0.21*\lam,0);
\path[left color=thin air,right color=thin air,middle color=dense air]
(\x,0) rectangle (\x+\lam,\D);
\foreach \i in {1,...,\N}{
\fill[blue!40!black] ({\x+acos(-rand)*\lam/180},{\D*(1+rand)/2}) circle(0.01);
}
}
\draw[wood] (0,0) rectangle++ (\L,\D);
\node[left=1,scale=0.8] at (0,\D/2) {$t=0$};
\end{scope}
% TUBE, t = T/2
\message{ Generating gas particles at t = T/2...^^J}
\begin{scope}[shift={(0,-2.8*\s)}]
\fill[dense air] (0,0) rectangle++ (\L,\D); % to fill seams
\foreach \i [evaluate={\x=(\i-1)*\lam;}] in {1,...,\n}{
\draw[myarr] (\x+0.25*\lam,1.1*\D) --++ (-0.21*\lam,0);
\draw[myarr] (\x+0.75*\lam,1.1*\D) --++ ( 0.21*\lam,0);
\path[left color=dense air,right color=dense air,middle color=thin air]
(\x,0) rectangle (\x+\lam,\D);
}
\foreach \i [evaluate={\x=(\i-2)*\lam;}] in {2,...,\n}{
\foreach \i in {1,...,\N}{
\fill[blue!40!black] ({\x+\lam/2+acos(-rand)*\lam/180},{\D*(1+rand)/2}) circle(0.01);
}
}
\foreach \i in {1,...,\N}{
\ifodd\i
\fill[blue!40!black] ({acos(-(rand+1)/2)*\lam/180-\lam/2},{\D*(1+rand)/2}) circle(0.01);
\else
\fill[blue!40!black] ({\L+acos(-(rand-1)/2)*\lam/180-\lam/2},{\D*(1+rand)/2}) circle(0.01);
\fi
}
\draw[wood] (0,0) rectangle++ (\L,\D);
\node[left=1,scale=0.8] at (0,\D/2) {$t=T/2$};
\end{scope}
\end{tikzpicture}
%%%%%%%%%%%%%%%%%%%%%%%%%%
% STANDING WAVE - CLOSED %
%%%%%%%%%%%%%%%%%%%%%%%%%%
% STANDING WAVE - CLOSED, n=1
\def\L{5.0} % pipe length
\def\R{0.6} % pipe radius
\def\wave#1{
\message{Standing wave #1 (closed)..^^J}
\pgfmathsetmacro\lam{2*\L/#1} % wavelength
\clip (-0.1,-1.3*\R) rectangle (1.27*\L,1.1*\R); % same canvas size
\fill[thin air] (0,-\R) rectangle (\L,\R);
\foreach \i in {1,...,#1}{
\path[left color=thin air,right color=dense air,
opacity=0.3,shading angle={(2*\i+1)*90}]
({(\i-1)*\lam/2},-\R) rectangle++ (\lam/2,2*\R);
}
\draw[Pline,samples=100,smooth,variable=\x,domain=0:\L]
plot(\x,{ (\R-0.041)*cos(360/(\lam)*\x)})
plot(\x,{-(\R-0.041)*cos(360/(\lam)*\x)});
\draw[wood] (-0.01,-\R) rectangle (\L+0.01,\R);
%\draw[->,thick] (0,-1.2*\R) -- (0,0.2+1.2*\R) node[left] {$\Delta P$};
%\draw[->,thick] (-0.2*\R,0) -- (0.2+\L,0) node[below] {$x$};
%\path (0,-1.3*\R) rectangle (1.3*\L,1.1*\R); % same canvas size
}
\begin{tikzpicture}
\draw[<->] (0,-1.3*\R) --++ (\L,0)
node[midway,below=-4,fill=white,inner sep=0.5,scale=0.8] {$L=\lambda/2$};
\wave{1}
\node[right=2,align=left] at (\L,0) {$n=1$\\[1mm]$\lambda=2L$};
\end{tikzpicture}
% STANDING WAVE - CLOSED, n=2
\begin{tikzpicture}
\wave{2}
\node[right=2,align=left] at (\L,0) {$n=2$\\[1mm]$\lambda=L$};
\end{tikzpicture}
% STANDING WAVE - CLOSED, n=3
\begin{tikzpicture}
\wave{3}
\node[below=3,right=2,align=left] at (\L,0) {$n=3$\\[2mm]$\lambda=\dfrac{2L}{3}$};
\end{tikzpicture}
% STANDING WAVE - CLOSED, n=4
\begin{tikzpicture}
\wave{4}
\node[below=3,right=2,align=left] at (\L,0) {$n=4$\\[2mm]$\lambda=\dfrac{L}{2}$};
\end{tikzpicture}
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% STANDING WAVE - HALF-OPEN %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% STANDING WAVE - HALF-OPEN, n=1
\def\wave#1{
\message{Standing wave #1 (half-open)..^^J}
\pgfmathsetmacro\lam{4*\L/(2*#1-1)} % wavelength
\clip (-0.1,-1.3*\R) rectangle (1.27*\L,1.1*\R); % same canvas size
\fill[thin air] (0,-\R) rectangle (\L,\R);
\begin{scope}
\clip (0,-\R) rectangle (\L,\R);
\foreach \i in {1,...,#1}{
\path[left color=thin air,right color=dense air,
opacity=0.3,shading angle={(2*\i+1)*90}]
({(\i-1)*\lam/2},-\R) rectangle++ (\lam/2,2*\R);
}
\end{scope}
\draw[Pline,samples=100,smooth,variable=\x,domain=0:\L]
plot(\x,{ (\R-0.041)*cos(360/(\lam)*\x)})
plot(\x,{-(\R-0.041)*cos(360/(\lam)*\x)});
\draw[wood,line cap=round]
(\L+0.01,\R) -| (-0.01,-\R) -- (\L+0.01,-\R);
%\draw[->,thick] (0,-1.2*\R) -- (0,0.2+1.2*\R) node[left] {$\Delta P$};
%\draw[->,thick] (-0.2*\R,0) -- (0.2+\L,0) node[below] {$x$};
}
\begin{tikzpicture}
\draw[<->] (0,-1.3*\R) --++ (\L,0)
node[midway,below=-4,fill=white,inner sep=0.5,scale=0.8] {$L=\lambda/4$};
\wave{1}
\node[right=2,align=left] at (\L,0) {$n=1$\\[1mm]$\lambda=4L$};
\end{tikzpicture}
% STANDING WAVE - HALF-OPEN, n=3
\begin{tikzpicture}
\wave{2}
\node[below=3,right=2,align=left] at (\L,0) {$n=3$\\[2mm]$\lambda=\dfrac{4L}{3}$};
\end{tikzpicture}
% STANDING WAVE - HALF-OPEN, n=5
\begin{tikzpicture}
\wave{3}
\node[below=3,right=2,align=left] at (\L,0) {$n=5$\\[2mm]$\lambda=\dfrac{4L}{5}$};
\end{tikzpicture}
% STANDING WAVE - HALF-OPEN, n=7
\begin{tikzpicture}
\wave{4}
\node[below=3,right=2,align=left] at (\L,0) {$n=7$\\[2mm]$\lambda=\dfrac{4L}{7}$};
\end{tikzpicture}
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% STANDING WAVE - OPEN-OPEN %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% STANDING WAVE - OPEN-OPEN, n=1
\def\wave#1{
\message{Standing wave #1 (open-open)..^^J}
\pgfmathsetmacro\lam{2*\L/#1} % wavelength
\clip (-0.1,-1.3*\R) rectangle (1.27*\L,1.1*\R); % same canvas size
\fill[thin air] (0,-\R) rectangle (\L,\R);
\begin{scope}
\clip (0,-\R) rectangle (\L,\R);
\foreach \i in {0,...,#1}{
\path[left color=thin air,right color=dense air,
opacity=0.3,shading angle={(2*\i+1)*90}]
({(\i-0.5)*\lam/2},-\R) rectangle++ (\lam/2,2*\R);
}
\end{scope}
\draw[Pline,samples=100,smooth,variable=\x,domain=0:\L]
plot(\x,{ (\R-0.041)*sin(360/(\lam)*\x)})
plot(\x,{-(\R-0.041)*sin(360/(\lam)*\x)});
\draw[wood,line cap=round]
(-0.01, \R) -- (\L+0.01, \R)
(-0.01,-\R) -- (\L+0.01,-\R);
%\draw[->,thick] (0,-1.2*\R) -- (0,0.2+1.2*\R) node[left] {$\Delta P$};
%\draw[->,thick] (-0.2*\R,0) -- (0.2+\L,0) node[below] {$x$};
}
\begin{tikzpicture}
\draw[<->] (0,-1.3*\R) --++ (\L,0)
node[midway,below=-4,fill=white,inner sep=0.5,scale=0.8] {$L=\lambda/2$};
\wave{1}
\node[right=2,align=left] at (\L,0) {$n=1$\\[1mm]$\lambda=2L$};
\end{tikzpicture}
% STANDING WAVE - OPEN-OPEN, n=2
\begin{tikzpicture}
\wave{2}
\node[right=2,align=left] at (\L,0) {$n=2$\\[2mm]$\lambda=L$};
\end{tikzpicture}
% STANDING WAVE - OPEN-OPEN, n=3
\begin{tikzpicture}
\wave{3}
\node[below=3,right=2,align=left] at (\L,0) {$n=3$\\[2mm]$\lambda=\dfrac{2L}{3}$};
\end{tikzpicture}
% STANDING WAVE - OPEN-OPEN, n=4
\begin{tikzpicture}
\wave{4}
\node[below=3,right=2,align=left] at (\L,0) {$n=4$\\[2mm]$\lambda=\dfrac{L}{2}$};
\end{tikzpicture}
\end{document}Click to download: waves_standing_air.tex • waves_standing_air.pdf
Open in Overleaf: waves_standing_air.tex.
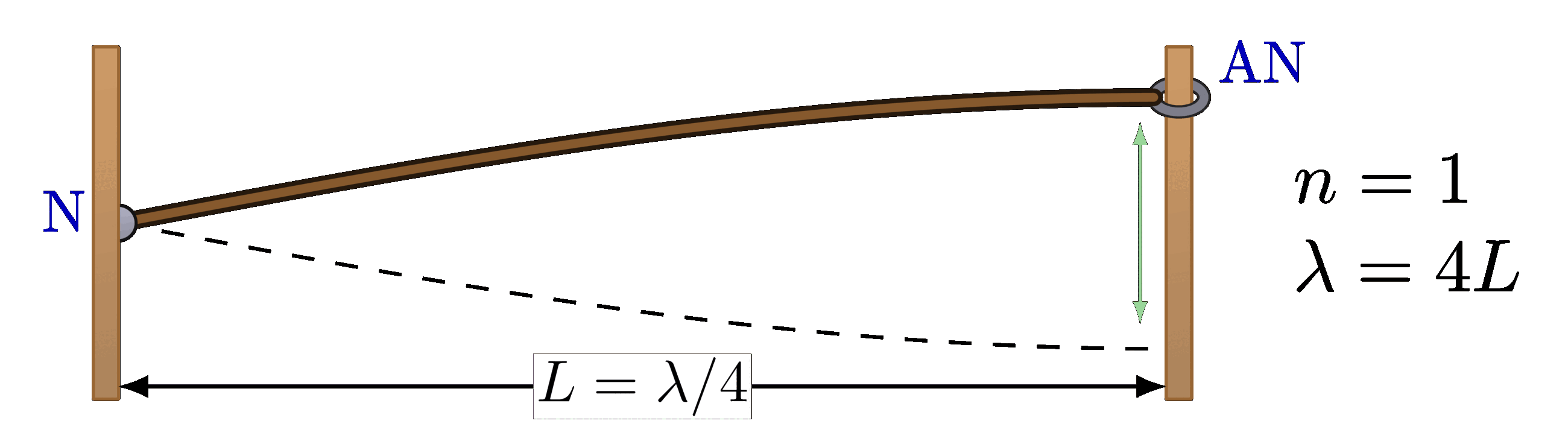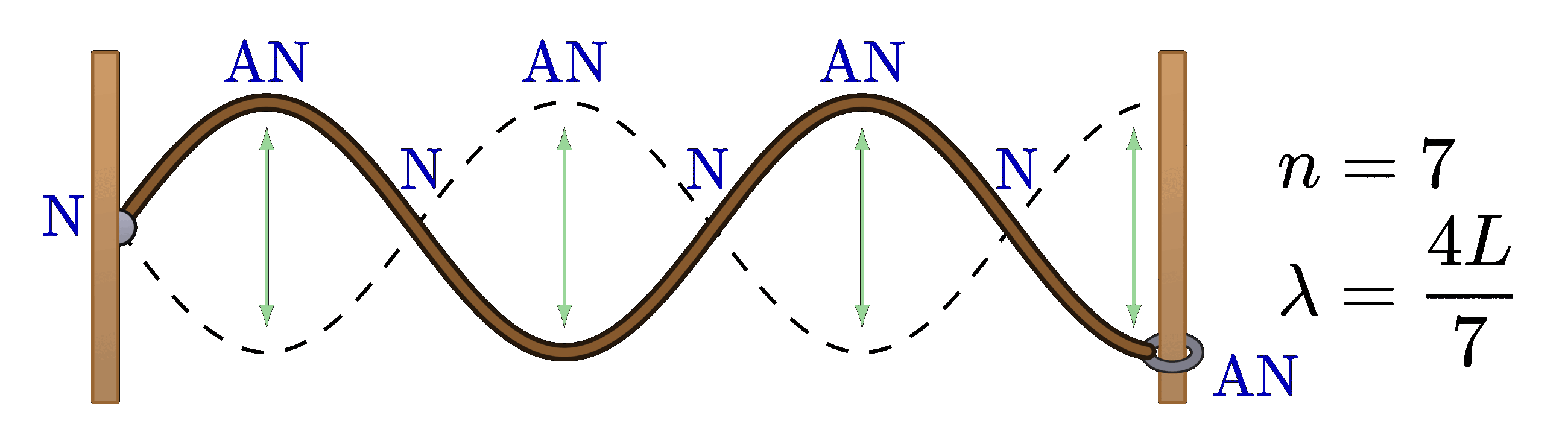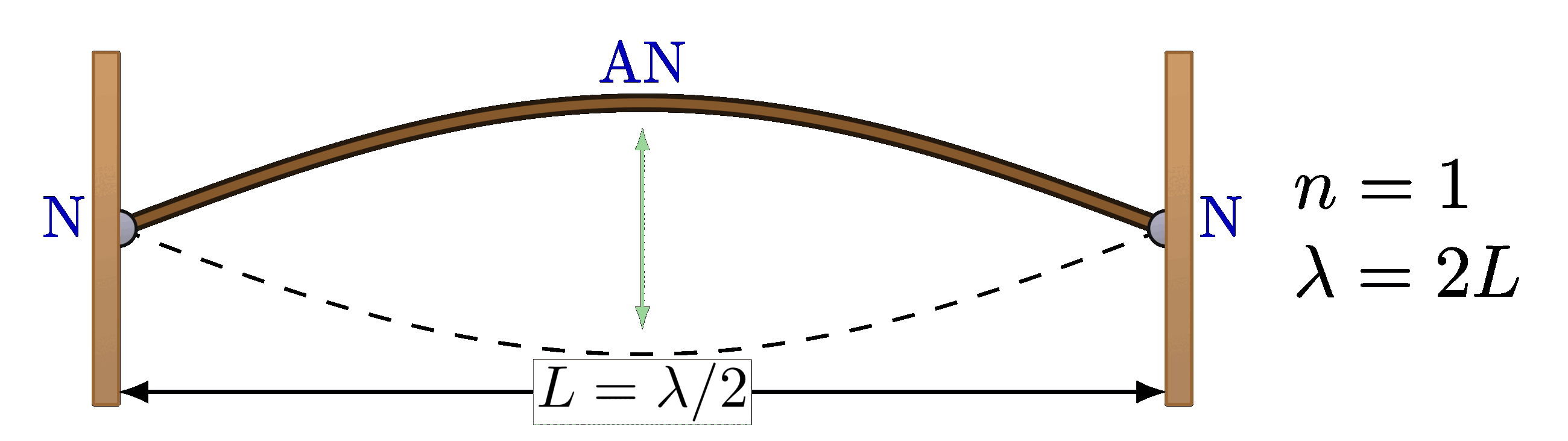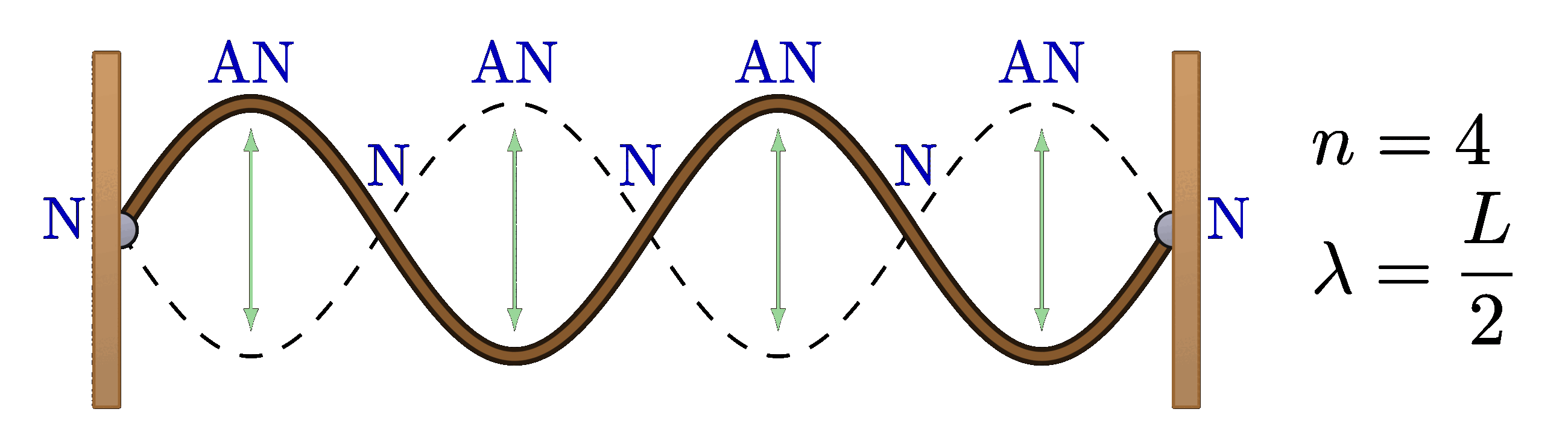
Hello Izaak,
Let me ask you something (not tikz related), in the first diagram of this series, I see that the arrows on the “tubes” t=0 and t = T/2 are always pointing from low to high pressure. Could explain why that is?
I just thought that pointing from high to low pressure would be the “correct” way.
Thank you,
Wagner.
Hi Wagner,
It is to indicate movement, or equivalently, the displacement (s) of air molecules which is 90° out of phase with pressure differences (ΔP), which is why I used blue arrows, like the blue graph of s vs. time. I guess it could be made more explicit and clear by indicating an “s” above the arrows.
Izaak