Edit and compile if you like:
\documentclass{article}
\usepackage{tikz}
\usetikzlibrary{intersections}
\usetikzlibrary{math}
\usepackage[active,tightpage]{preview}
\PreviewEnvironment{tikzpicture}
\setlength\PreviewBorder{0.125pt}
%
% File name: perigals-dissection.tex
% Description:
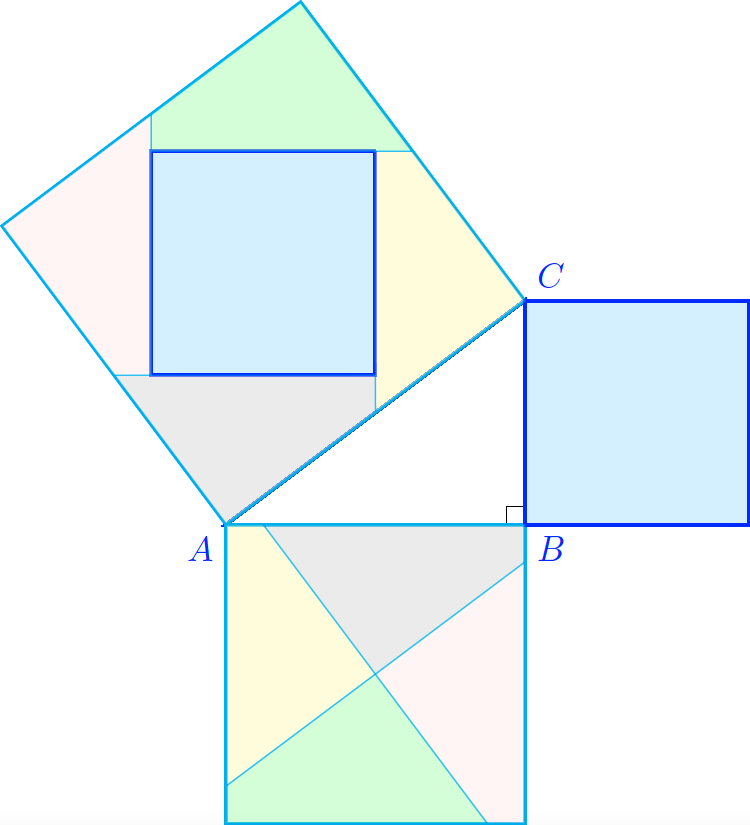
% A geometric proof of the Pythagorean theorem
% known as the Perigal's dissection is shown.
%
% Date of creation: July, 30th, 2021.
% Date of last modification: October, 9th, 2022.
% Author: Efraín Soto Apolinar.
% https://www.aprendematematicas.org.mx/author/efrain-soto-apolinar/instructing-courses/
% Source: page 126 of the
% Glosario Ilustrado de Matem\'aticas Escolares.
% https://tinyurl.com/5udm2ufy
%
% Terms of use:
% According to TikZ.net
% https://creativecommons.org/licenses/by-nc-sa/4.0/
% Your commitment to the terms of use is greatly appreciated.
%
\begin{document}
%
\begin{tikzpicture}[scale=0.75]
\tikzmath{function rotacionx(\x,\y,\angulo) {return \x*cos(\angulo) + \y*sin(\angulo);};}
\tikzmath{function rotaciony(\x,\y,\angulo) {return -\x*sin(\angulo) + \y*cos(\angulo);};}
\pgfmathsetmacro{\dx}{0.25}
% Vertices of the triangle
\pgfmathsetmacro{\Ax}{0}
\pgfmathsetmacro{\Ay}{0}
\coordinate (A) at (\Ax,\Ay);
\pgfmathsetmacro{\Bx}{4}
\pgfmathsetmacro{\By}{0}
\coordinate (B) at (\Bx,\By);
\pgfmathsetmacro{\Cx}{4}
\pgfmathsetmacro{\Cy}{3}
\coordinate (C) at (\Cx,\Cy);
% Lengths of the sides
\pgfmathsetmacro{\lAB}{sqrt((\Bx - \Ax)*(\Bx - \Ax) + (\By - \Ay)*(\By - \Ay))}
\pgfmathsetmacro{\lAC}{sqrt((\Cx - \Ax)*(\Cx - \Ax) + (\Cy - \Ay)*(\Cy - \Ay))}
\pgfmathsetmacro{\lBC}{sqrt((\Cx - \Bx)*(\Cx - \Bx) + (\Cy - \By)*(\Cy - \By))}
% Slopes of the sides of the triangle
\pgfmathsetmacro{\mAC}{(\Cy - \Ay)/(\Cx - \Ax)}
\pgfmathsetmacro{\mAB}{(\By - \Ay)/(\Bx - \Ax)}
%
\pgfmathsetmacro{\angA}{atan(\mAC)}
\pgfmathsetmacro{\angB}{90.0}
\pgfmathsetmacro{\angC}{90.0-\angA}
\pgfmathsetmacro{\angAH}{45+\angA}
% Coordinates of the vertices of the squares
\pgfmathsetmacro{\Dx}{0}
\pgfmathsetmacro{\Dy}{-\lAB}
\coordinate (D) at (\Dx,\Dy);
\pgfmathsetmacro{\Ex}{\Bx}
\pgfmathsetmacro{\Ey}{-\lAB}
\coordinate (E) at (\Ex,\Ey);
\pgfmathsetmacro{\Fx}{\Bx+\lBC}
\pgfmathsetmacro{\Fy}{0}
\coordinate (F) at (\Fx,\Fy);
\pgfmathsetmacro{\Gx}{\Bx+\lBC}
\pgfmathsetmacro{\Gy}{\lBC}
\coordinate (G) at (\Gx,\Gy);
\pgfmathsetmacro{\Hx}{sqrt(2.0)*\lAC*cos(45+\angA)}
\pgfmathsetmacro{\Hy}{sqrt(2.0)*\lAC*sin(45+\angA)}
\coordinate (H) at (\Hx,\Hy);
\pgfmathsetmacro{\Ix}{rotacionx(\Cx,\Cy,-90)}
\pgfmathsetmacro{\Iy}{rotaciony(\Cx,\Cy,-90)}
\coordinate (I) at (\Ix,\Iy);
% Coordinates of the centroid of the square upon the hypotenuse
\pgfmathsetmacro{\Mx}{0.5*(\Ax+\Hx)}
\pgfmathsetmacro{\My}{0.5*(\Ay+\Hy)}
\coordinate (M) at (\Mx,\My);
% Points upon the hypotenuse to draw the dissection
\pgfmathsetmacro{\Jx}{\Mx+0.5*\lBC}
\pgfmathsetmacro{\Jy}{\My+0.5*\lBC}
\coordinate (J) at (\Jx,\Jy);
\pgfmathsetmacro{\Kx}{\Mx-0.5*\lBC}
\pgfmathsetmacro{\Ky}{\My+0.5*\lBC}
\coordinate (K) at (\Kx,\Ky);
\pgfmathsetmacro{\Lx}{\Mx-0.5*\lBC}
\pgfmathsetmacro{\Ly}{\My-0.5*\lBC}
\coordinate (L) at (\Lx,\Ly);
\pgfmathsetmacro{\Nx}{\Mx+0.5*\lBC}
\pgfmathsetmacro{\Ny}{\My-0.5*\lBC}
\coordinate (N) at (\Nx,\Ny);
% Length for dissection
\pgfmathsetmacro{\mCH}{(\Hy - \Cy)/(\Hx - \Cx)}
\pgfmathsetmacro{\xp}{\Cx+(\Jy-\Cy)/\mCH}
\pgfmathsetmacro{\yp}{\Jy}
\pgfmathsetmacro{\ld}{sqrt((\Jx - \xp)*(\Jx - \xp) + (\Jy - \yp) * (\Jy - \yp))}
% Vertices of the dissection upon the leg
\pgfmathsetmacro{\Cunox}{\Bx}
\pgfmathsetmacro{\Cunoy}{\By - \ld}
\coordinate (Cuno) at (\Cunox,\Cunoy);
\pgfmathsetmacro{\Cdosx}{\Ax + \ld}
\pgfmathsetmacro{\Cdosy}{\Ay}
\coordinate (Cdos) at (\Cdosx,\Cdosy);
\pgfmathsetmacro{\Ctresx}{\Dx}
\pgfmathsetmacro{\Ctresy}{\Dy + \ld}
\coordinate (Ctres) at (\Ctresx,\Ctresy);
\pgfmathsetmacro{\Ccuatrox}{\Ex - \ld}
\pgfmathsetmacro{\Ccuatroy}{\Ey}
\coordinate (Ccuatro) at (\Ccuatrox,\Ccuatroy);
\path[name path=UT] (Cuno) -- (Ctres);
\path[name path=DC] (Cdos) -- (Ccuatro);
\path[name intersections={of=UT and DC}];
\coordinate (Q) at (intersection-1);
%
\pgfmathsetmacro{\ejex}{max(\Ax,\Bx,\Cx) + 1.0}
\pgfmathsetmacro{\ejey}{max(\Ay,\By,\Cy) + 1.0}
% The right triangle
\draw[black] (\Bx-\dx,0) -- (\Bx-\dx,\dx) -- (\Bx,\dx);
\draw[blue,thick] (A) -- (B) -- (C) -- cycle;
\fill[blue] (A) circle (1.0pt) node[below left]{$A$};
\fill[blue] (B) circle (1.0pt) node[below right]{$B$};
\fill[blue] (C) circle (1.0pt) node[above right]{$C$};
% Squares on the sides of the right triangle
\draw[cyan,thick] (0,0) rectangle (\lAB,-\lAB); % lado AB
\draw[cyan,thick,rotate=\angA] (0,0) rectangle (\lAC,\lAC); % lado AC
\draw[blue,thick,fill=cyan!15,shift={(\Bx,\By)}] (0,0) rectangle (\lBC,\lBC); % lado BC
% Rectangle of dissection
\draw[blue,thick,fill=cyan!15] (J) -- (K) -- (L) -- (N) -- (J);
% Compute the intersections to draw the dissection
\coordinate (Jp) at (\Jx+2.0,\Jy);
\path[name path=CH] (C) -- (H);
\path[name path=JJp] (J) -- (Jp);
\path[name intersections={of=CH and JJp}];
\coordinate (Huno) at (intersection-1);
%
\coordinate (Np) at (\Nx,\Ny-2.0);
\path[name path=AC] (A) -- (C);
\path[name path=NNp] (N) -- (Np);
\path[name intersections={of=AC and NNp}];
\coordinate (Hdos) at (intersection-1);
%
\coordinate (Lp) at (\Lx-2.0,\Ly);
\path[name path=AI] (A) -- (I);
\path[name path=LLp] (L) -- (Lp);
\path[name intersections={of=AI and LLp}];
\coordinate (Htres) at (intersection-1);
%
\coordinate (Kp) at (\Kx,\Ky+2.0);
\path[name path=HI] (H) -- (I);
\path[name path=KKp] (K) -- (Kp);
\path[name intersections={of=HI and KKp}];
\coordinate (Hcuatro) at (intersection-1);
% Disection upon the hypotenuse
\draw[cyan,fill=yellow!35,opacity=0.5] (C) -- (Huno) -- (J) -- (Hdos) -- cycle;
\draw[cyan,fill=gray!35,opacity=0.5] (A) -- (Hdos) -- (N) -- (Htres) -- cycle;
\draw[cyan,fill=pink!35,opacity=0.5] (I) -- (Htres) -- (L) -- (Hcuatro) -- cycle;
\draw[cyan,fill=green!35,opacity=0.5] (H) -- (Huno) -- (K) -- (Hcuatro) -- cycle;
% Disection upon the longest leg (AB)
\draw[cyan,fill=gray!35,opacity=0.5] (Q) -- (Cuno) -- (B) -- (Cdos) -- cycle;
\draw[cyan,fill=yellow!35,opacity=0.5] (Q) -- (Cdos) -- (A) -- (Ctres) -- cycle;
\draw[cyan,fill=green!35,opacity=0.5] (Q) -- (Ctres) -- (D) -- (Ccuatro) -- cycle;
\draw[cyan,fill=pink!35,opacity=0.5] (Q) -- (Ccuatro) -- (E) -- (Cuno) -- cycle;
%
\end{tikzpicture}
%
\end{document}
Click to download: perigals-dissection.tex • perigals-dissection.pdf
Open in Overleaf: perigals-dissection.tex
See more on the author page of Efraín Soto Apolinar.