Centripetal force

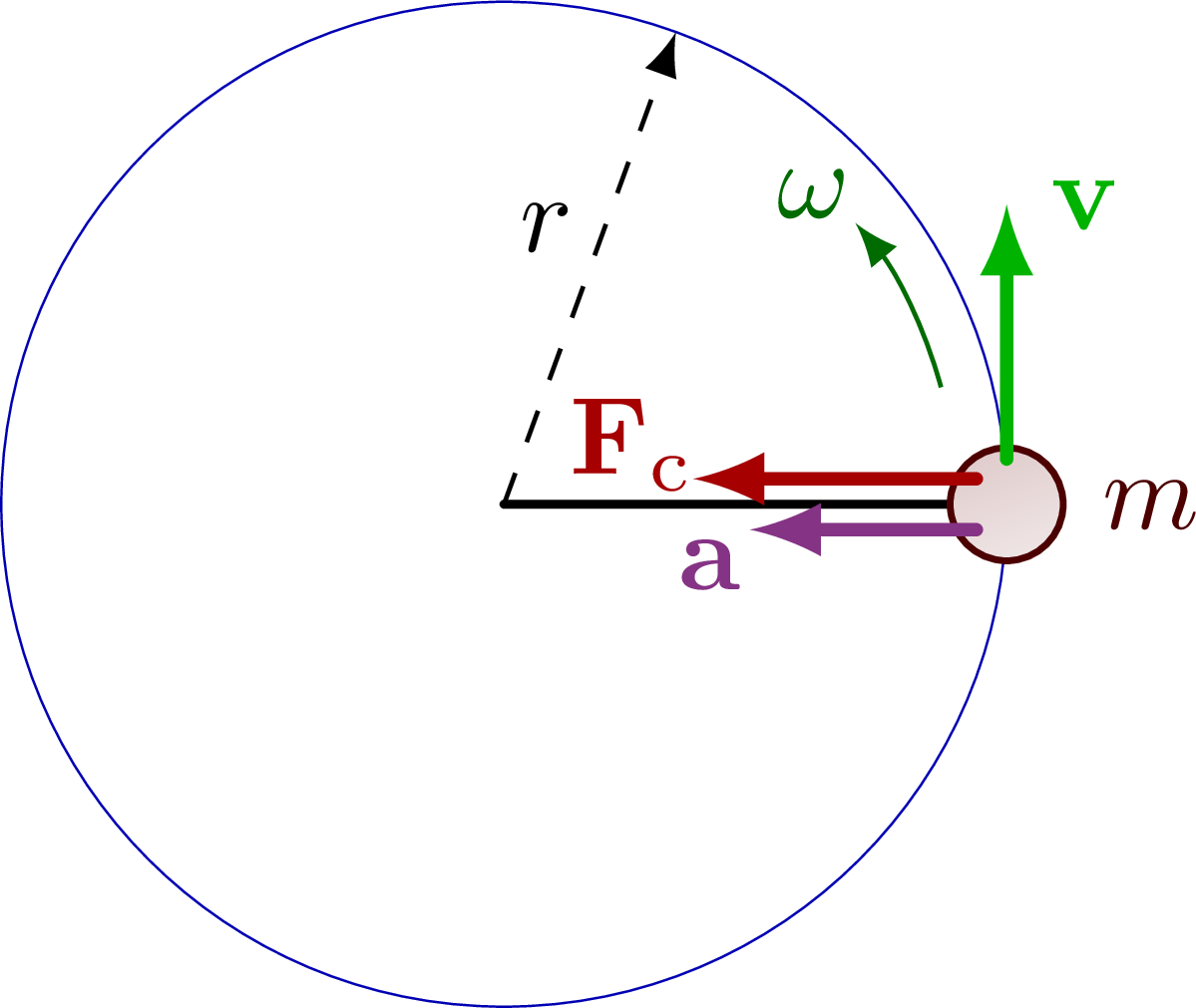
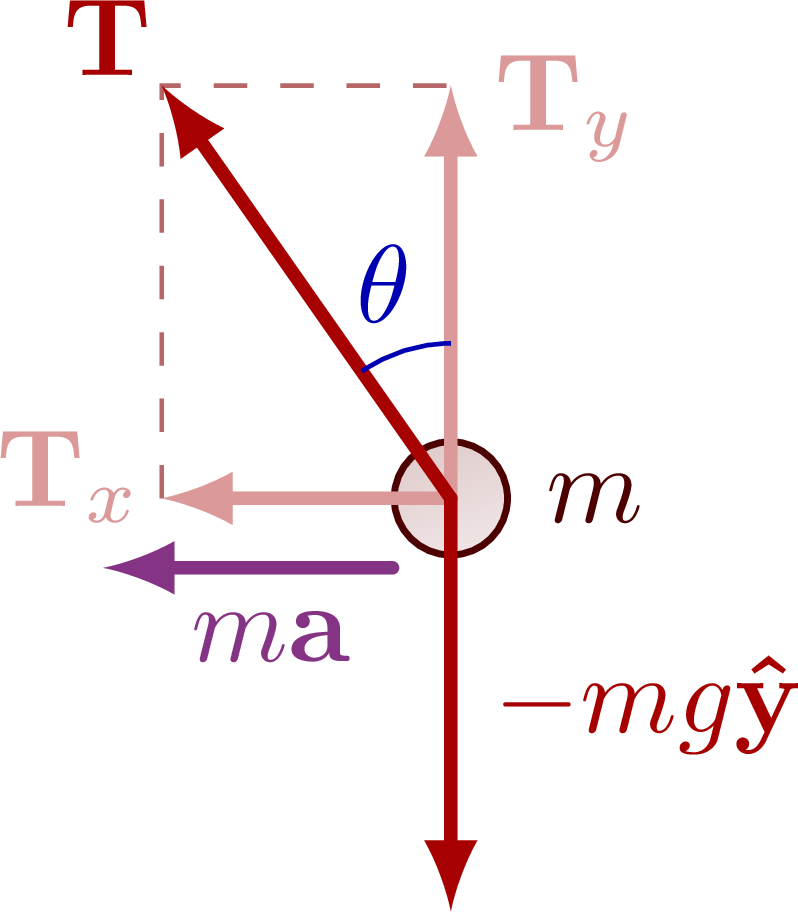
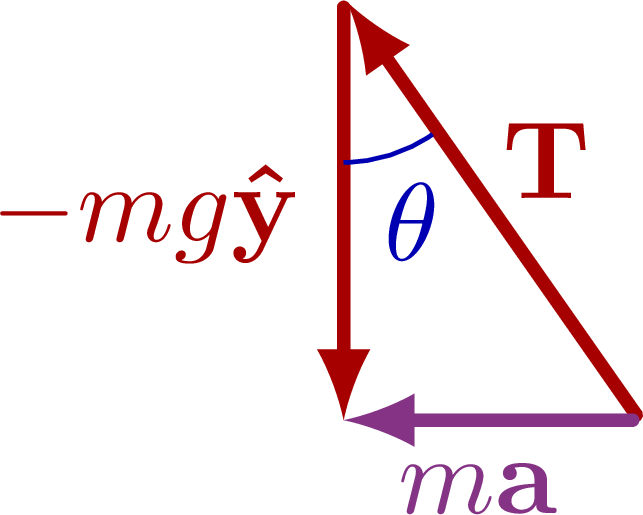The basics of the centripetal force in uniform circular motion, including a mass suspended from a string.
More on uniform circular motion here. For more related figures, please see the “forces” and “Newton’s laws” tag.

Edit and compile if you like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
% Author: Izaak Neutelings (October 2020)
% Inspiration: https://tex.stackexchange.com/questions/25531/adding-underbrace-in-tikz
\documentclass[border=3pt,tikz]{standalone}
\usepackage{physics}
\usepackage{siunitx}
\usepackage{ifthen}
\usepackage{tikz}
%\usepackage[outline]{contour} % glow around text
\usetikzlibrary{calc}
\usetikzlibrary{angles,quotes} % for pic
\usetikzlibrary{patterns}
\tikzset{>=latex} % for LaTeX arrow head
%\contourlength{1.4pt}
\colorlet{xcol}{blue!70!black}
\colorlet{vcol}{green!70!black}
\colorlet{myred}{red!65!black}
\colorlet{acol}{red!50!blue!80!black!80}
\tikzstyle{ground}=[preaction={fill,top color=black!10,bottom color=black!5,shading angle=20},
                    fill,pattern=north east lines,draw=none,minimum width=0.3,minimum height=0.6]
\tikzstyle{metal}=[fill,top color=black!40,bottom color=black!20,shading angle=10]
\tikzstyle{mass}=[line width=0.6,red!30!black,fill=red!40!black!10,rounded corners=1,
                  top color=red!40!black!20,bottom color=red!40!black!10,shading angle=20]
\tikzstyle{rope}=[brown!70!black,very thick,line cap=round]
\def\rope#1{ \draw[black,line width=1.5] #1; \draw[rope] #1; }
% FORCES SWITCH
\tikzstyle{force}=[->,myred,very thick,line cap=round]
\tikzstyle{Fproj}=[force,myred!40]
\newcommand{\vbF}{\vb{F}}
\newcommand{\vbT}{\vb{T}}
\begin{document}
% CIRCULAR MOTION - 2D
\begin{tikzpicture}
  \def\R{1.6}  % string length
  \def\r{0.18} % ball radius
  \def\Ry{0.5} % small radius of the ellipse
  \def\F{0.9}  % force size
 
 
הההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההה
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX