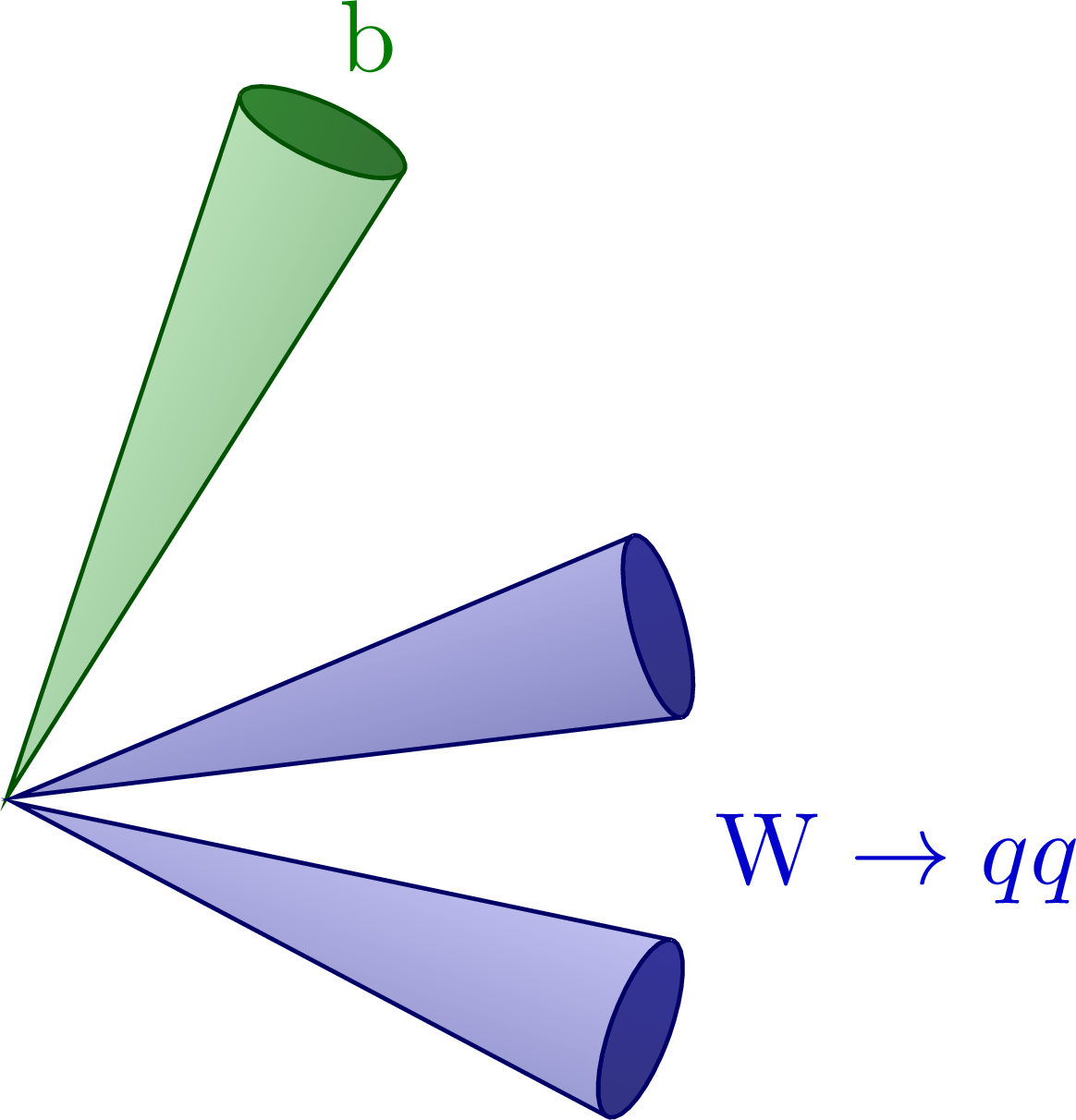
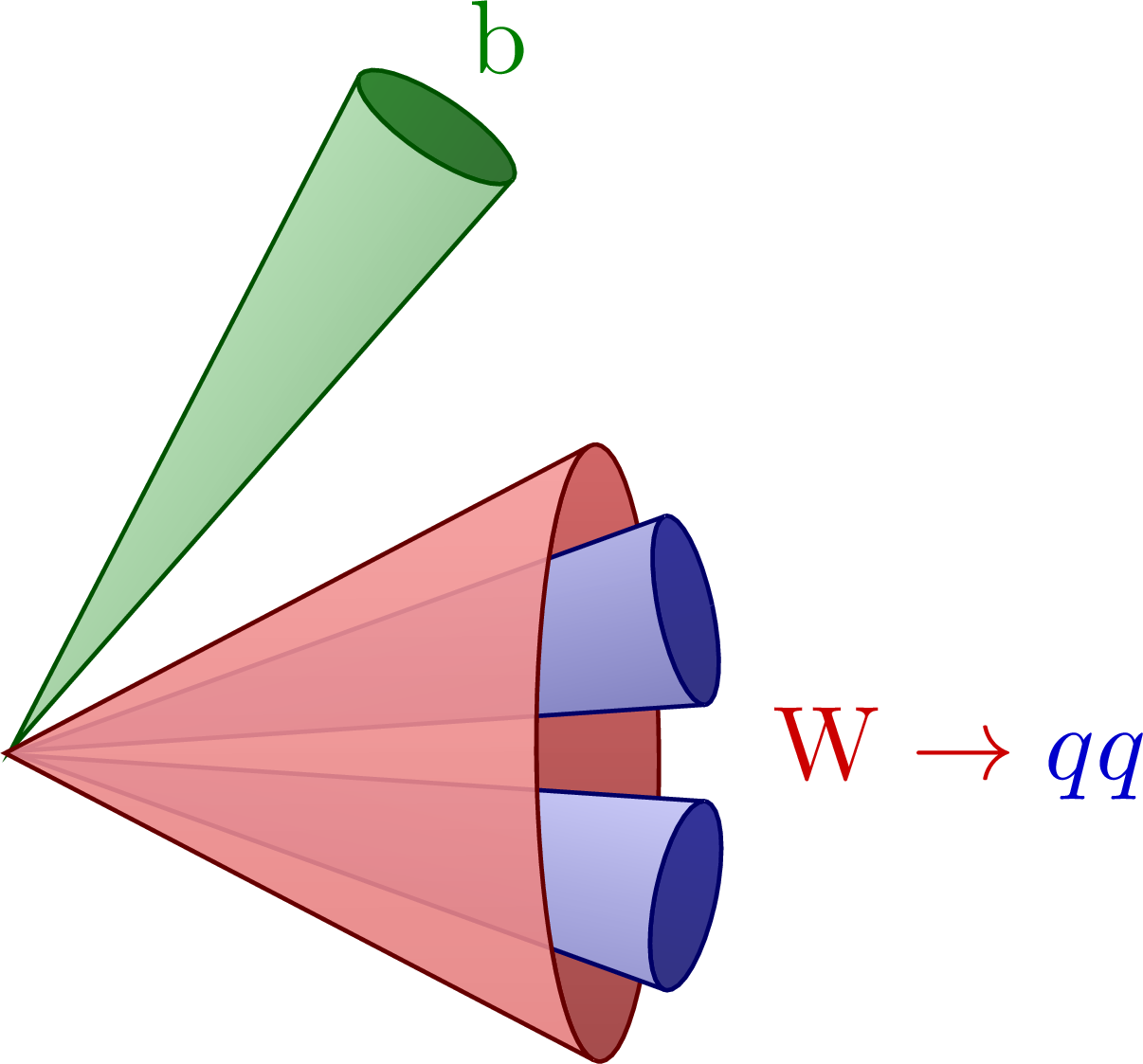
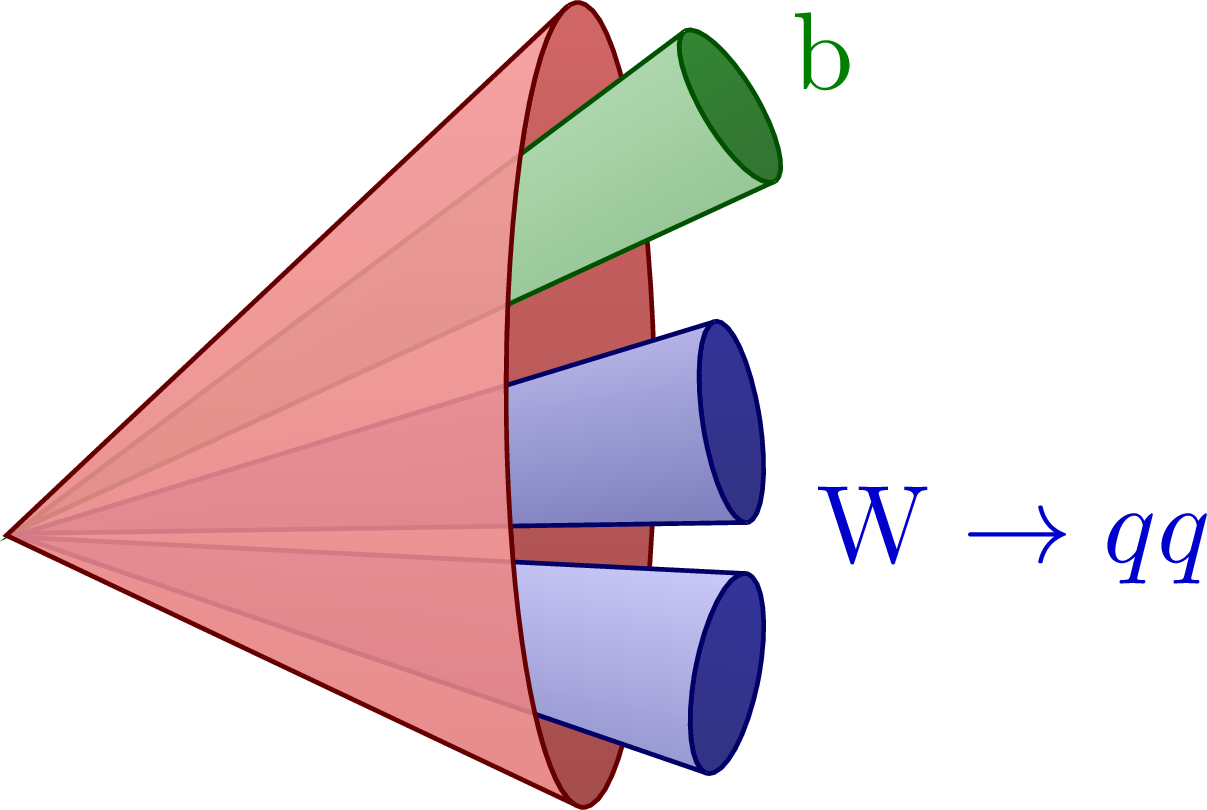
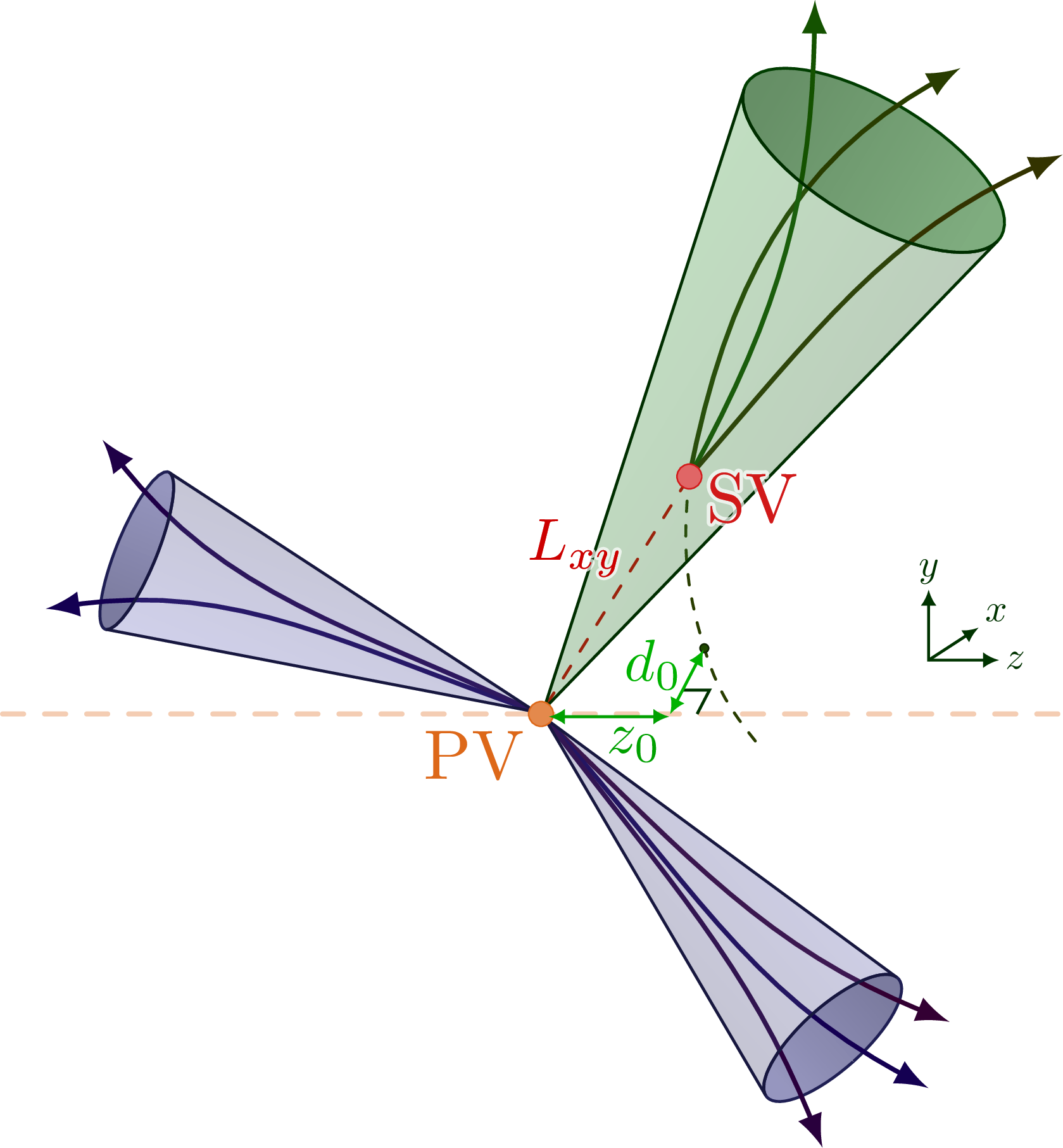
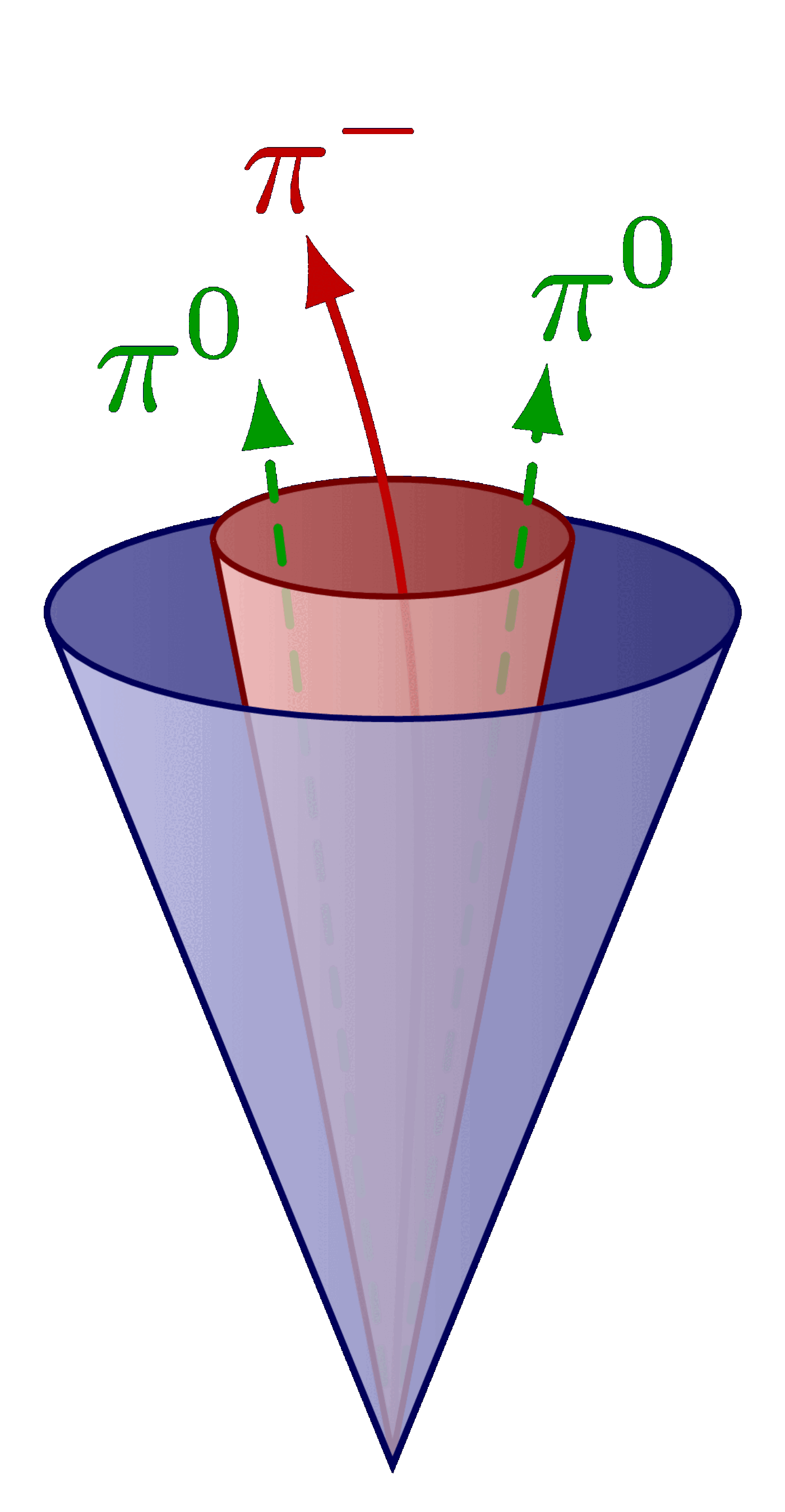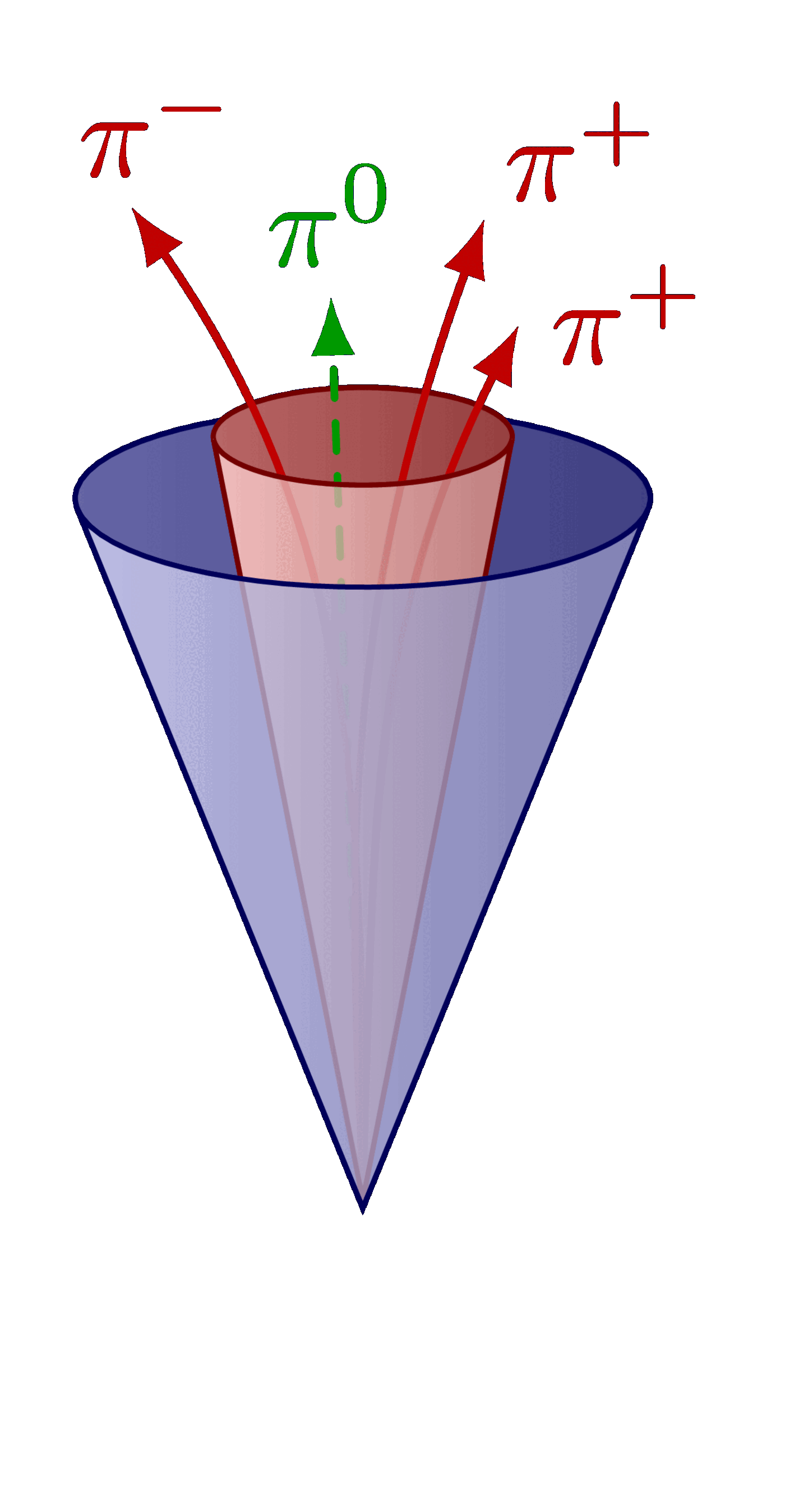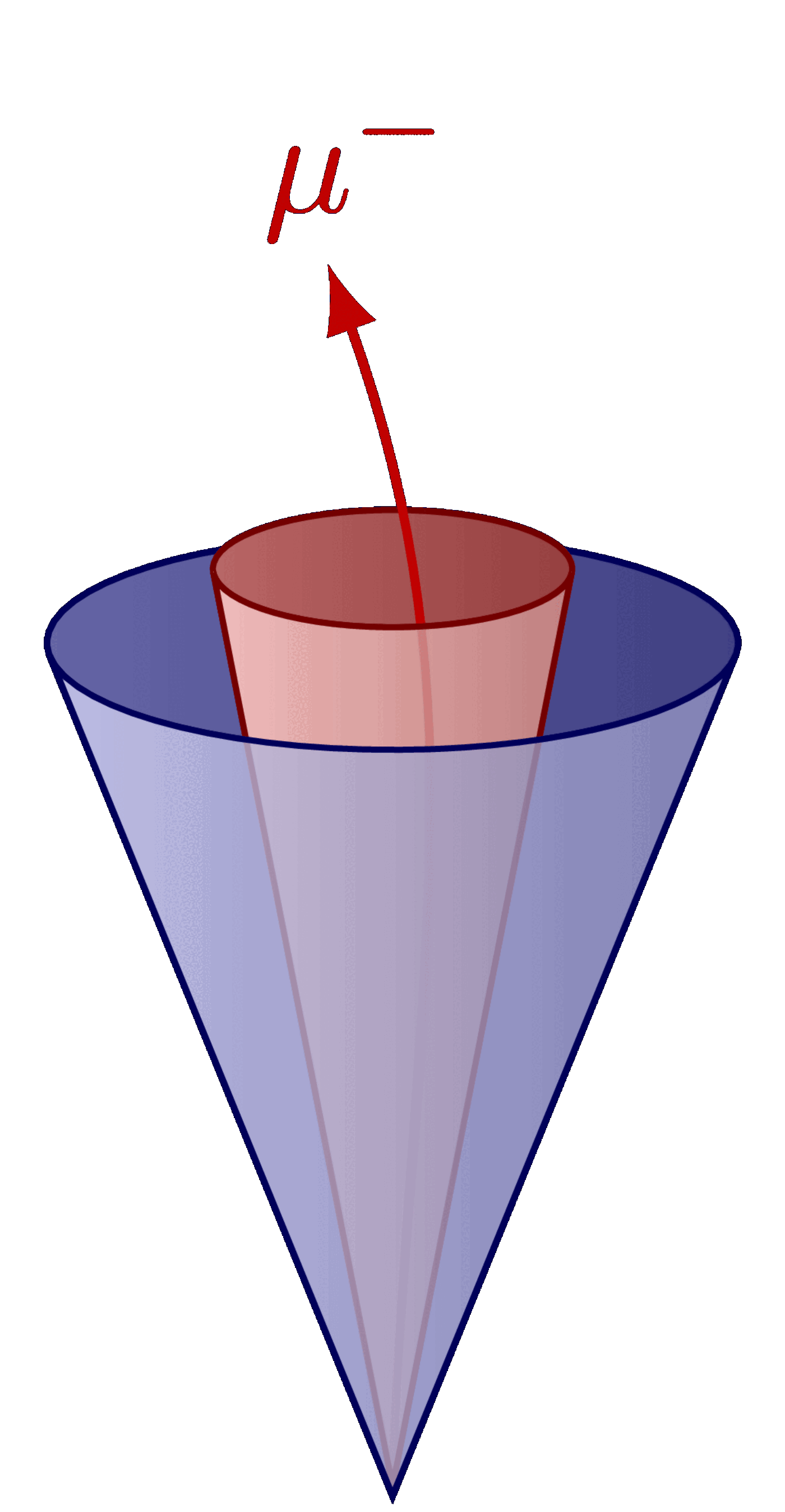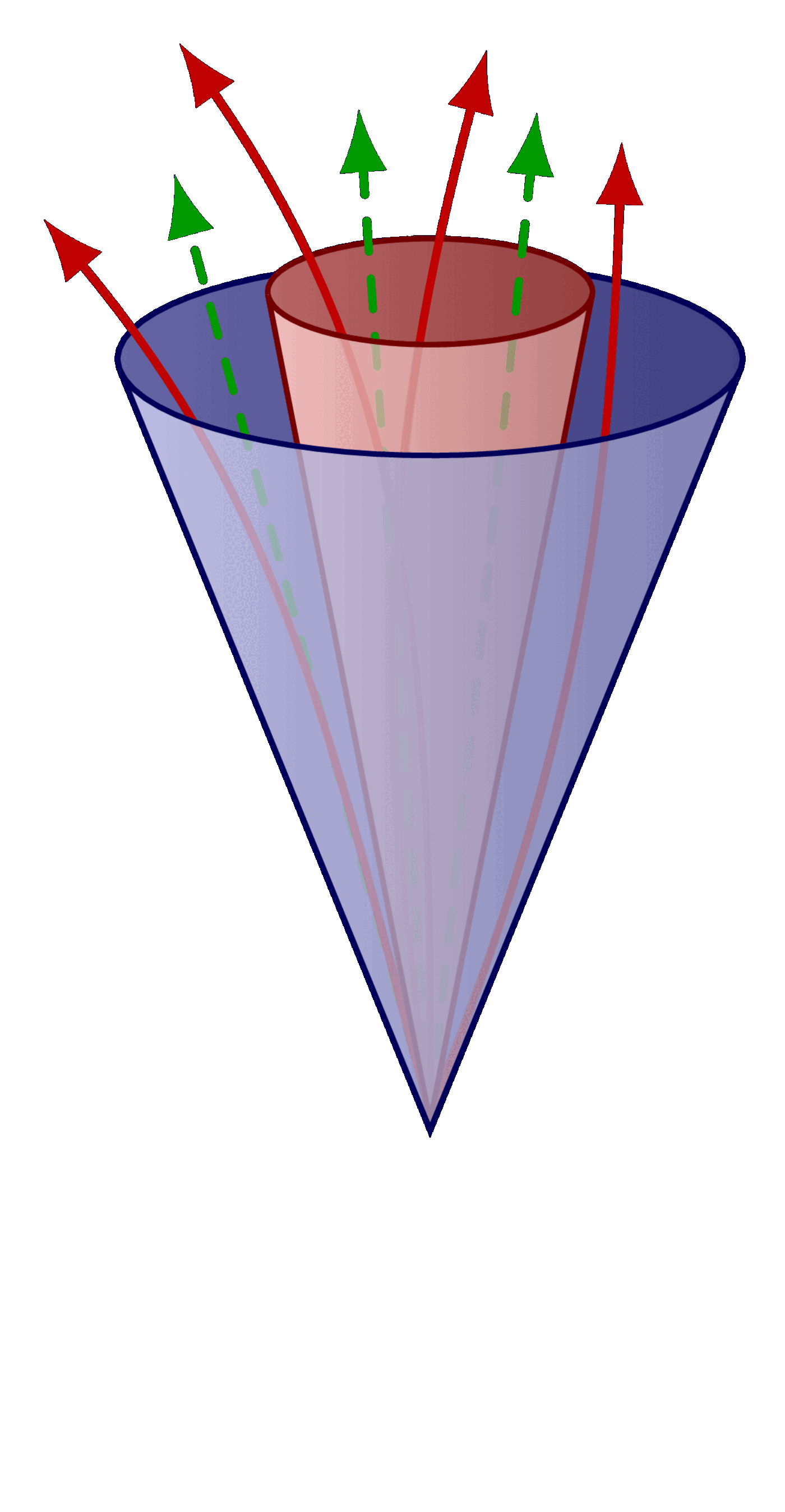
Different boosted jet regimes of the hadronic top decay.
For more related figures, please see the “jet” tag or the Particle Physics category. The cones are constructed with the tangent methods presented here.
Edit and compile if you like:
% Author: Izaak Neutelings (May 2021)
% Description: hadronic top quark jet
\documentclass[border=3pt,tikz]{standalone}
\usepackage{amsmath}
\usepackage{physics}
\usepackage{xcolor}
\usetikzlibrary{calc}
\usetikzlibrary{math} % for \tikzmath
\tikzset{>=latex} % for LaTeX arrow head
\usetikzlibrary{decorations.pathreplacing} % for curly braces
\colorlet{myblue}{blue!70!black}
\colorlet{mydarkblue}{blue!40!black}
\colorlet{mygreen}{green!40!black}
\colorlet{myred}{red!65!black}
\tikzstyle{cone}=[thin,blue!50!black,fill=blue!50!black!30] %,fill opacity=0.8
\tikzstyle{conebase}=[cone,fill=blue!50!black!50] %,fill opacity=0.8
\newcommand\jetcone[5][blue]{{
\pgfmathanglebetweenpoints{\pgfpointanchor{#2}{center}}{\pgfpointanchor{#3}{center}}
\edef\ang{#4/2} % half-opening angle
\edef\e{#5} % ratio a/b ("eccentricity") of cone top
\edef\vang{\pgfmathresult} % angle of vector OV
\tikzmath{
coordinate \C;
\C = (#2)-(#3);
\x = veclen(\Cx,\Cy)*\e*sin(\ang)^2; % x coordinate P
\y = tan(\ang)*(veclen(\Cx,\Cy)-\x); % y coordinate P
\a = veclen(\Cx,\Cy)*sqrt(\e)*sin(\ang); % vertical radius
\b = veclen(\Cx,\Cy)*tan(\ang)*sqrt(1-\e*sin(\ang)^2); % horizontal radius
\angb = acos(sqrt(\e)*sin(\ang)); % angle of P in ellipse
}
\coordinate (tmpL) at ($(#3)-(\vang:\x pt)+(\vang+90:\y pt)$); % tangency
\draw[thin,#1!40!black,rotate=\vang, %,fill=#1!50!black!80
top color=#1!50!black!80,bottom color=#1!40!black!80,shading angle=\vang]
(#3) ellipse({\a pt} and {\b pt});
\draw[thin,#1!40!black,rotate=\vang,rounded corners=0.001pt,%fill=#1!80!black!40,
top color=#1!90!black!20,bottom color=#1!50!black!50,shading angle=\vang]
(tmpL) arc(180-\angb:180+\angb:{\a pt} and {\b pt})
-- (#2) -- cycle;
}}
\begin{document}
% RESOLVED TOP JETS
\begin{tikzpicture}[scale=2.3]
\coordinate (O) at (0,0);
\coordinate (BJ) at ( 65:1.1); % b jet
\coordinate (J1) at ( 15:1.0); % q jet 1
\coordinate (J2) at (-20:1.0); % q jet 2
\jetcone[green!80!black]{O}{BJ}{14}{0.10}
\jetcone{O}{J1}{16}{0.08}
\jetcone{O}{J2}{16}{0.10}
\node[green!50!black] at (65:1.26) {b};
\node[blue!80!black,right] at (-5:1.00) {$\mathrm{W} \to qq$};
\end{tikzpicture}
% BOOSTED TOP JETS, partially merged
\begin{tikzpicture}[scale=2.3]
\coordinate (O) at (0,0);
\coordinate (BJ) at ( 56:1.1); % b jet
\coordinate (J1) at ( 12:1.0); % q jet 1
\coordinate (J2) at (-12:1.0); % q jet 2
\coordinate (M) at (0:0.85); % merged
% LARGE CONE BACK
\def\ang{28} % opening angle
\def\e{0.05} % eccentricity cone opening
\tikzmath{
coordinate \C;
\C = (O)-(M);
\x = veclen(\Cx,\Cy)*\e*sin(\ang)^2; % x coordinate P
\y = tan(\ang)*(veclen(\Cx,\Cy)-\x); % y coordinate P
\a = veclen(\Cx,\Cy)*sqrt(\e)*sin(\ang); % vertical radius
\b = veclen(\Cx,\Cy)*tan(\ang)*sqrt(1-\e*sin(\ang)^2); % horizontal radius
\angb = acos(sqrt(\e)*sin(\ang)); % angle of P in ellipse
}
\coordinate (ML) at ($(M)+(-180:\x pt)+(90:\y pt)$); % tangency
\draw[thin,red!40!black, %,fill=red!70!black!60
top color=red!70!black!60,bottom color=red!50!black!70] % base
(M) ellipse({\a pt} and {\b pt});
% JETS
\jetcone[green!80!black]{O}{BJ}{14}{0.10} % b jet
\jetcone{O}{J1}{16}{0.08}
\jetcone{O}{J2}{16}{0.10}
\node[green!50!black] at (56:1.26) {b};
\node[blue!80!black,right] at (0:1.05) {${\color{red!80!black}\mathrm{W} \to}\; qq$};
% LARGE CONE FRONT
\draw[thin,red!40!black,fill opacity=0.9,rounded corners=0.001pt, %,fill=red!90!black!40
top color=red!90!black!40,bottom color=red!80!black!50]
(ML) arc(180-\angb:180+\angb:{\a pt} and {\b pt})
-- ($(O)-(0.0005,0)$) -- cycle;
\end{tikzpicture}
% BOOSTED TOP JETS, fully merged
\begin{tikzpicture}[scale=2.3]
\coordinate (O) at (0,0);
\coordinate (BJ) at ( 29:1.15); % b jet
\coordinate (J1) at ( 11:1.00); % q jet 1
\coordinate (J2) at ( -8:1.00); % q jet 2
% LARGE CONE BACK
\def\ang{32} % opening angle
\def\e{0.05} % eccentricity cone opening
\def\vang{10} % large cone angle
\coordinate (M) at (\vang:0.80); % merged
\tikzmath{
coordinate \C;
\C = (O)-(M);
\x = veclen(\Cx,\Cy)*\e*sin(\ang)^2; % x coordinate P
\y = tan(\ang)*(veclen(\Cx,\Cy)-\x); % y coordinate P
\a = veclen(\Cx,\Cy)*sqrt(\e)*sin(\ang); % vertical radius
\b = veclen(\Cx,\Cy)*tan(\ang)*sqrt(1-\e*sin(\ang)^2); % horizontal radius
\angb = acos(sqrt(\e)*sin(\ang)); % angle of P in ellipse
}
\coordinate (ML) at ($(M)+(\vang-180:\x pt)+(\vang+90:\y pt)$); % tangency
\draw[thin,red!40!black,rotate=\vang, %,fill=red!70!black!60
top color=red!70!black!60,bottom color=red!50!black!70,shading angle=\vang] % base
(M) ellipse({\a pt} and {\b pt});
% JETS
\jetcone[green!80!black]{O}{BJ}{12}{0.10} % b jet
\jetcone{O}{J1}{16}{0.08}
\jetcone{O}{J2}{16}{0.10}
\node[green!50!black] at (31:1.3) {b};
\node[blue!80!black,right] at (0:1.05) {$\mathrm{W} \to qq$};
% LARGE CONE FRONT
\draw[thin,red!40!black,fill opacity=0.9,rotate=\vang,rounded corners=0.001pt, %,fill=red!90!black!40
top color=red!90!black!40,bottom color=red!80!black!50,shading angle=\vang]
(ML) arc(180-\angb:180+\angb:{\a pt} and {\b pt})
-- ($(O)-(0.0005,0)$) -- cycle;
\end{tikzpicture}
\end{document}Click to download: jets_top.tex • jets_top.pdf
Open in Overleaf: jets_top.tex