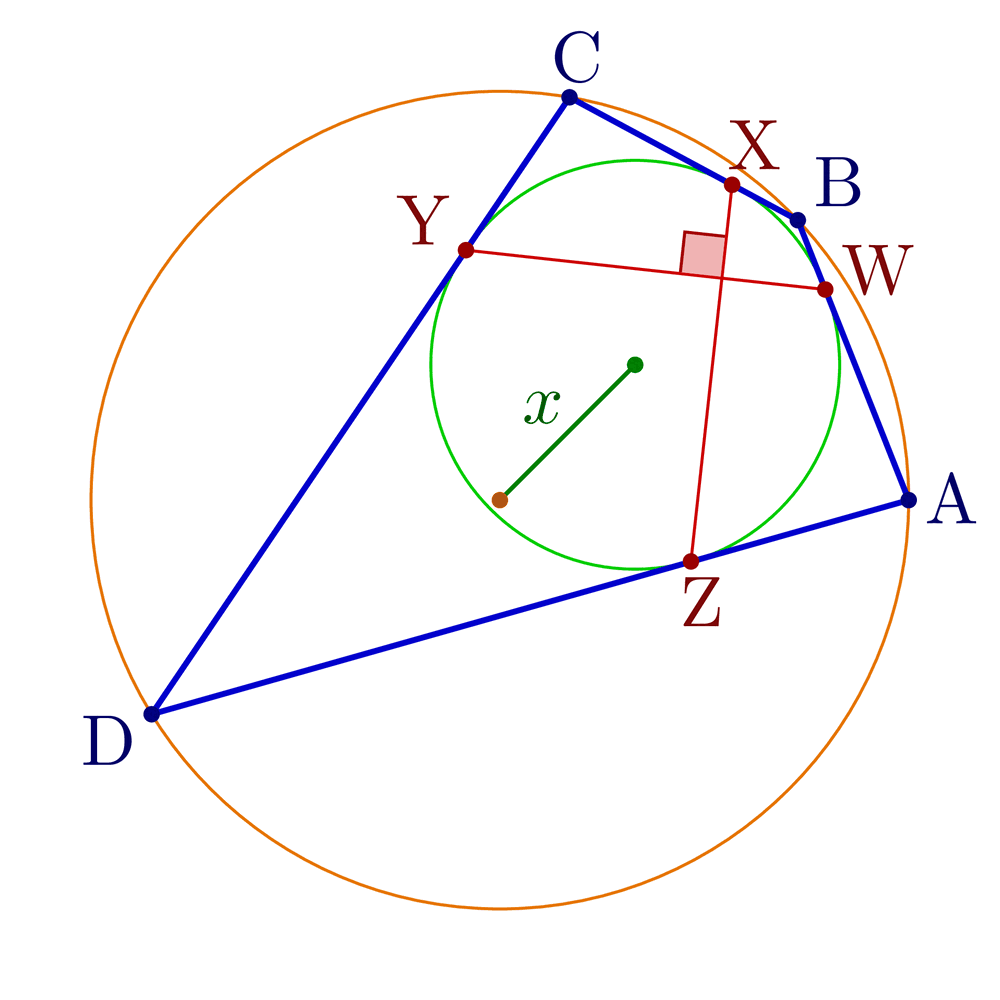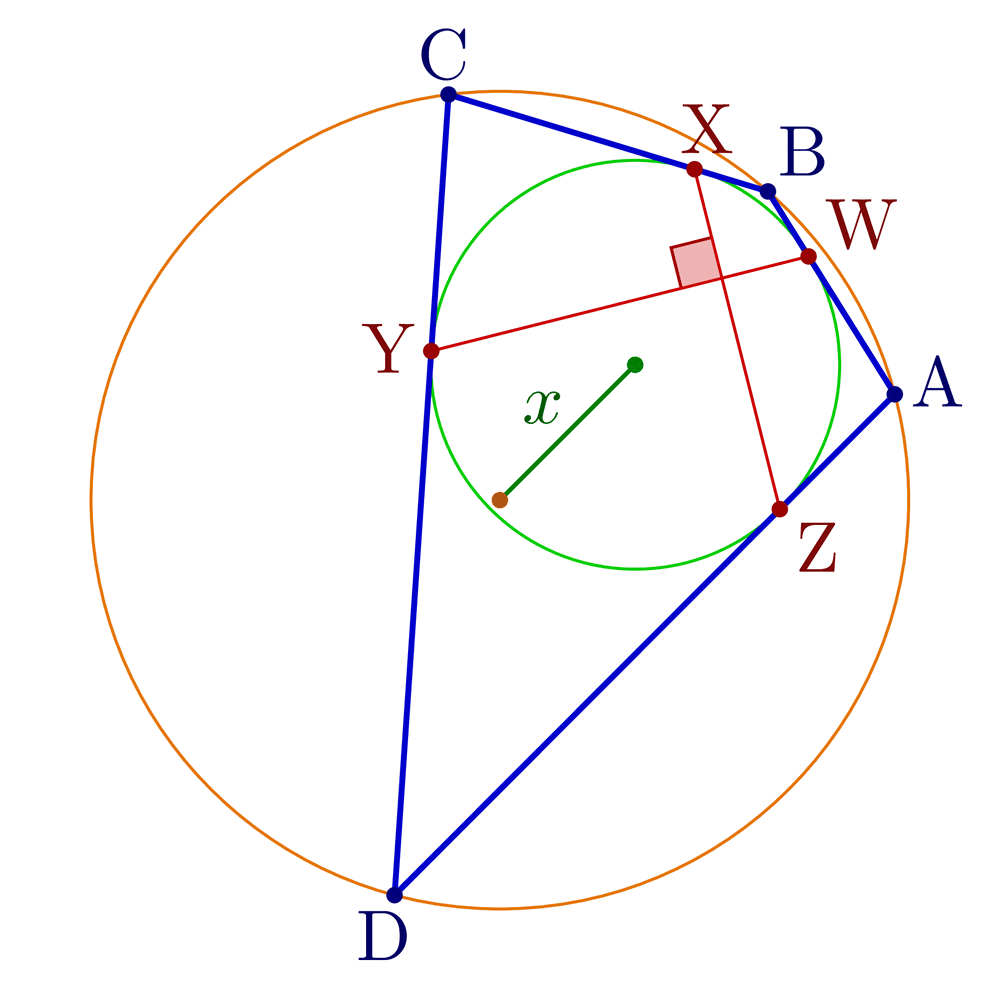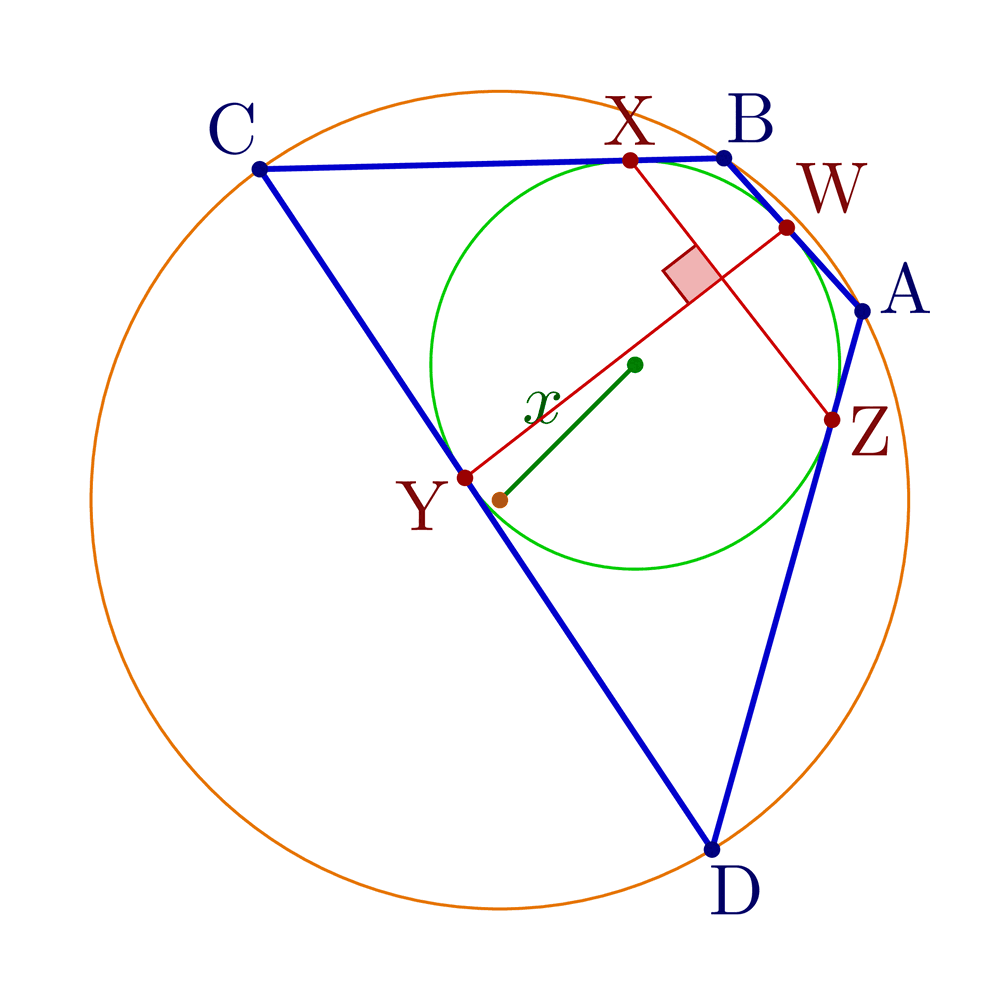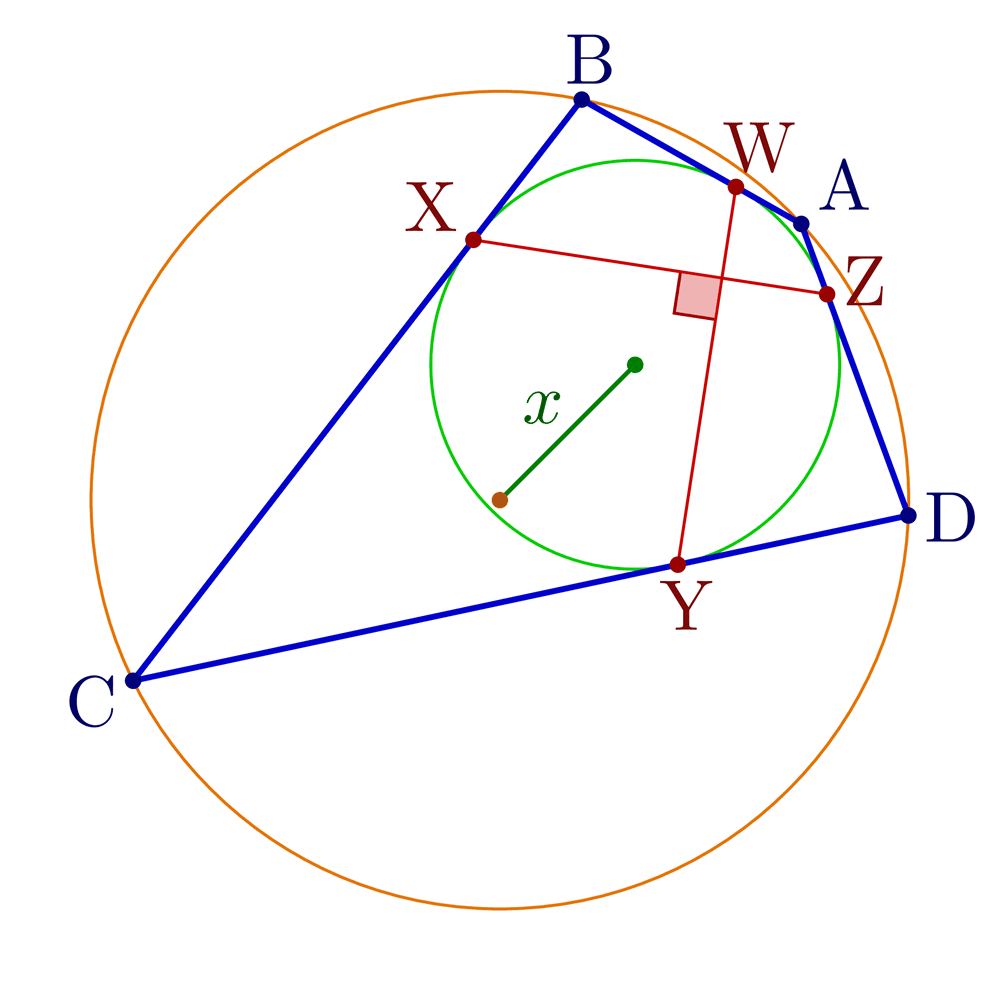
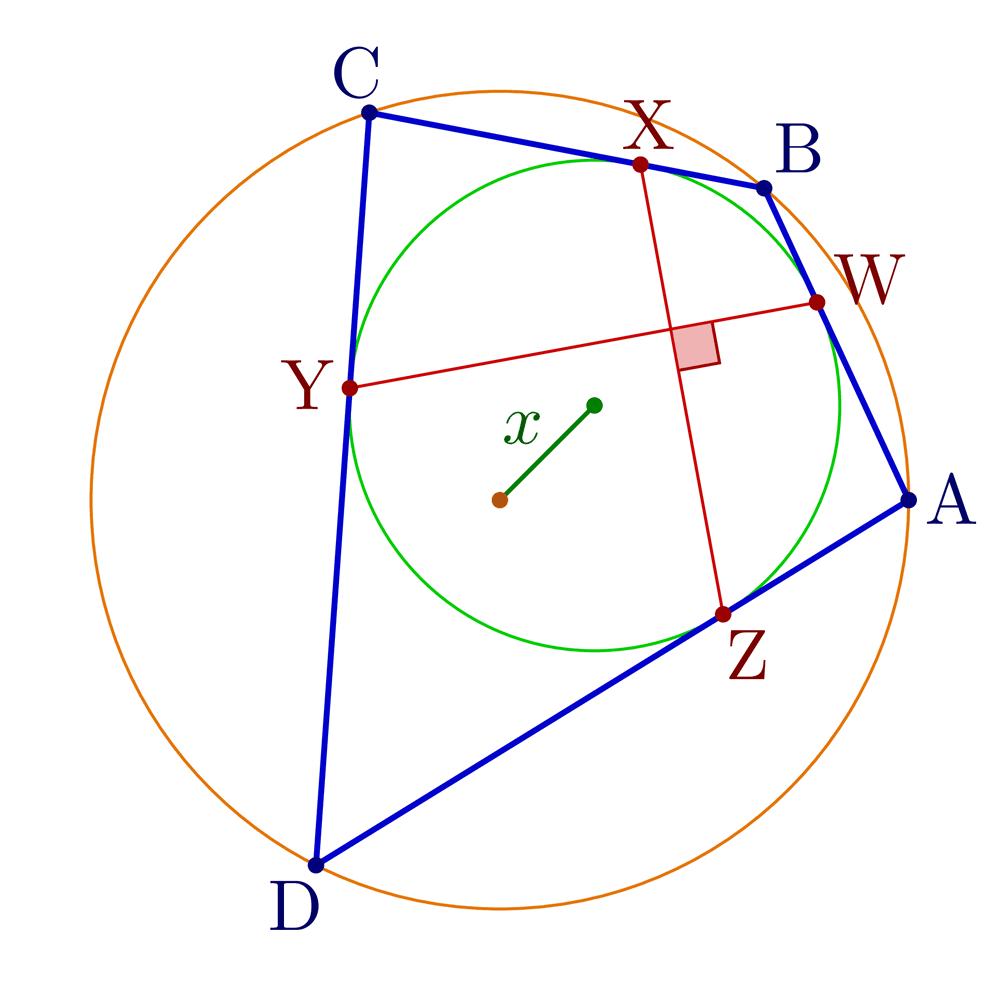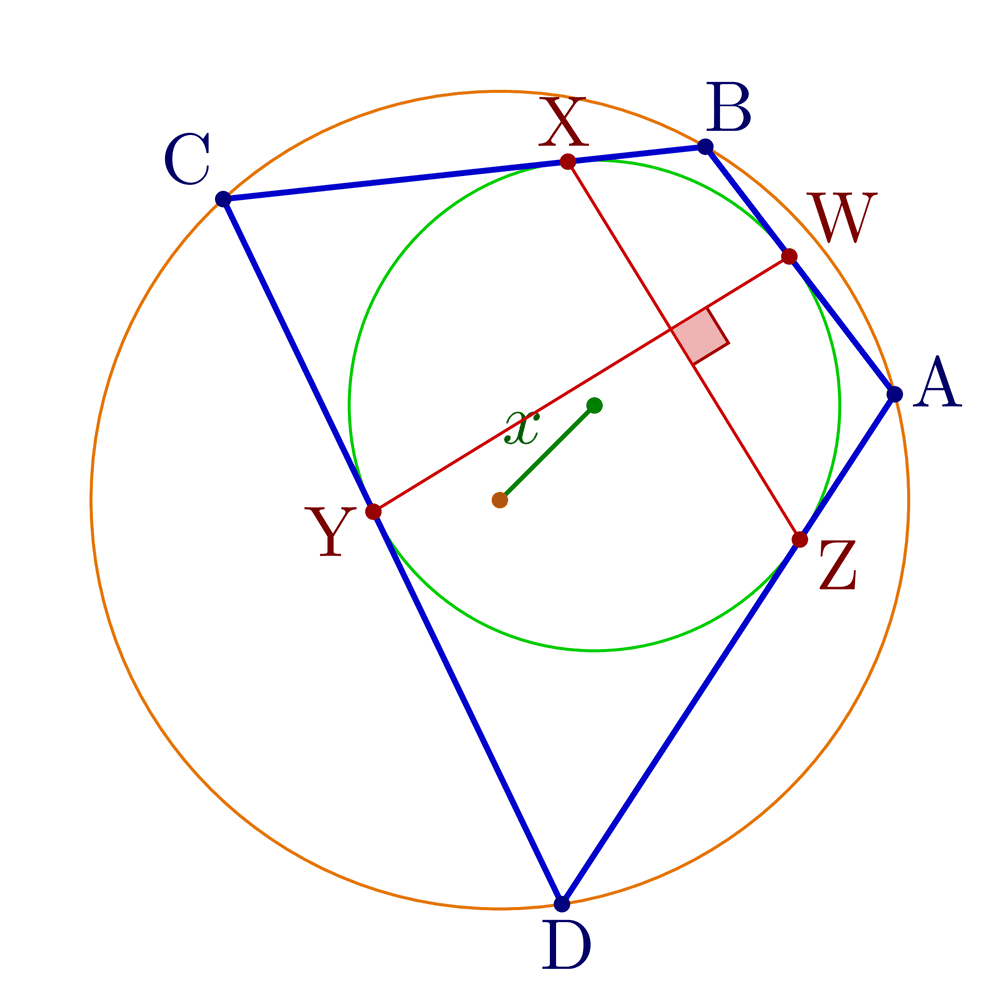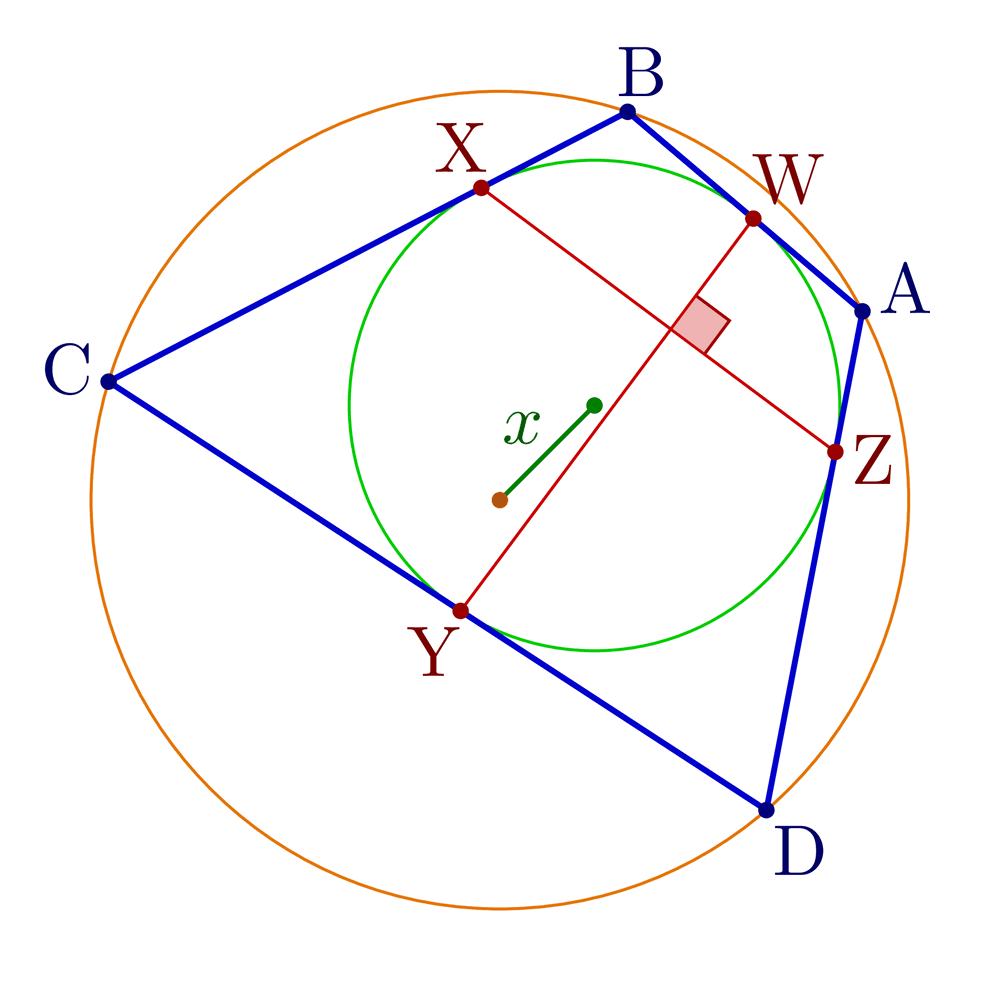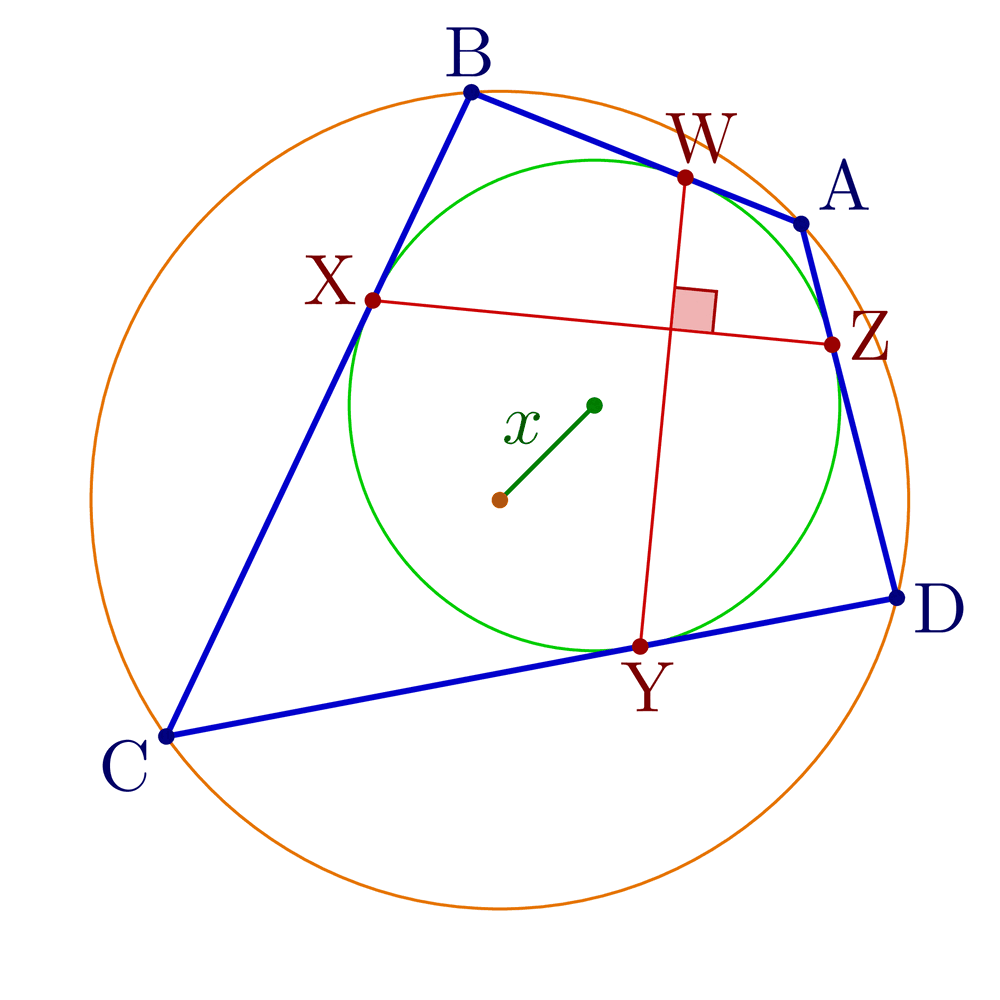
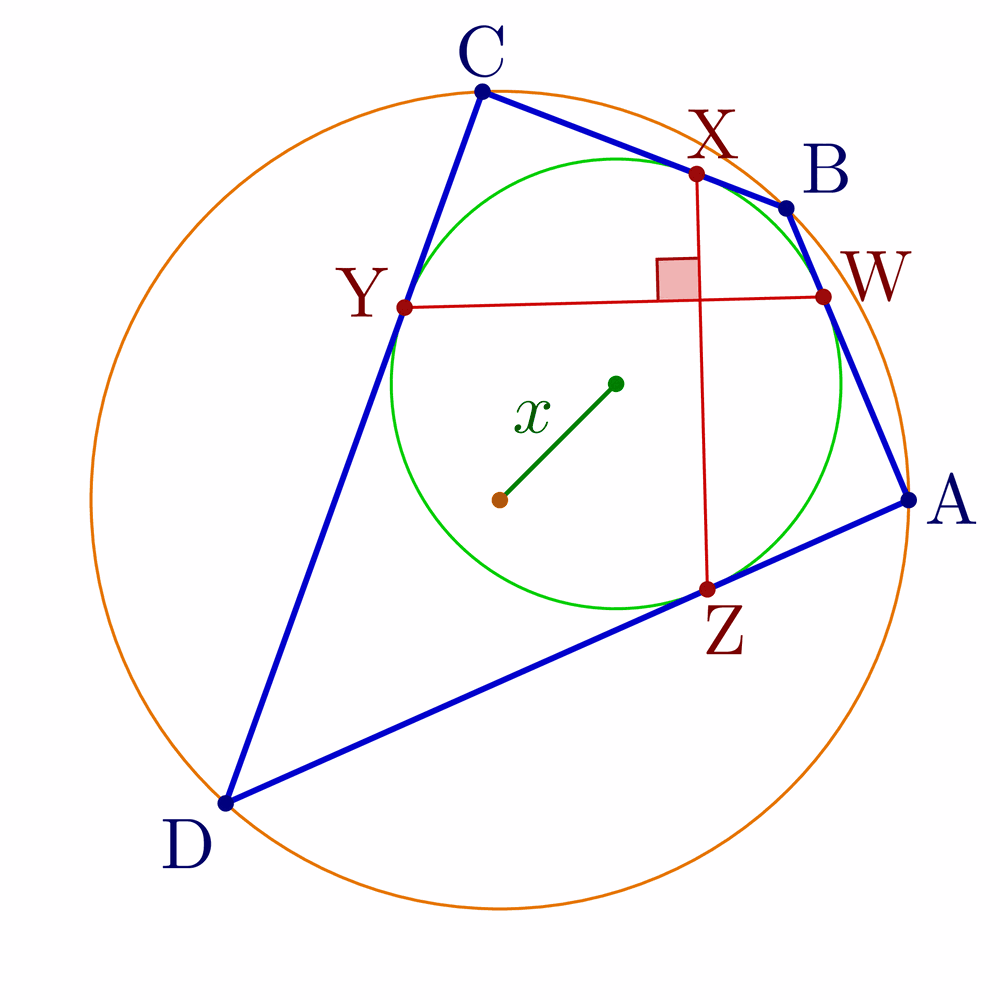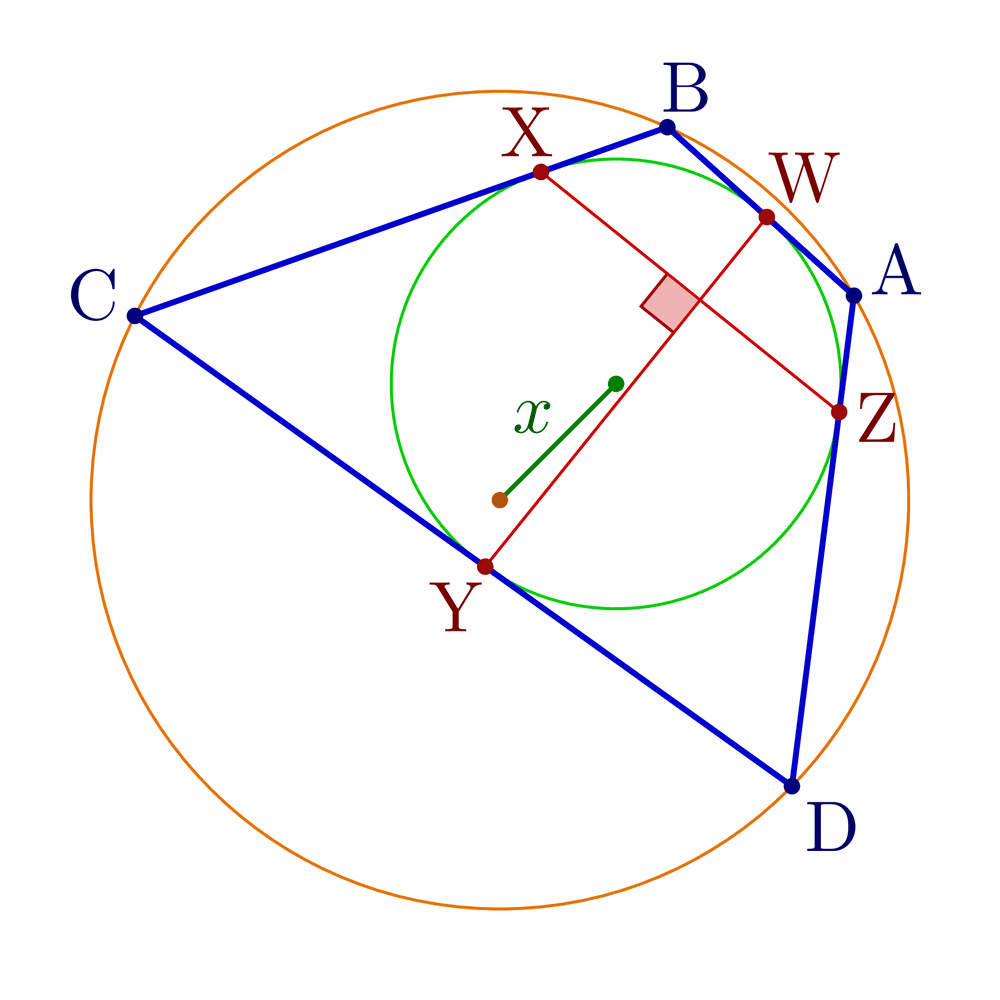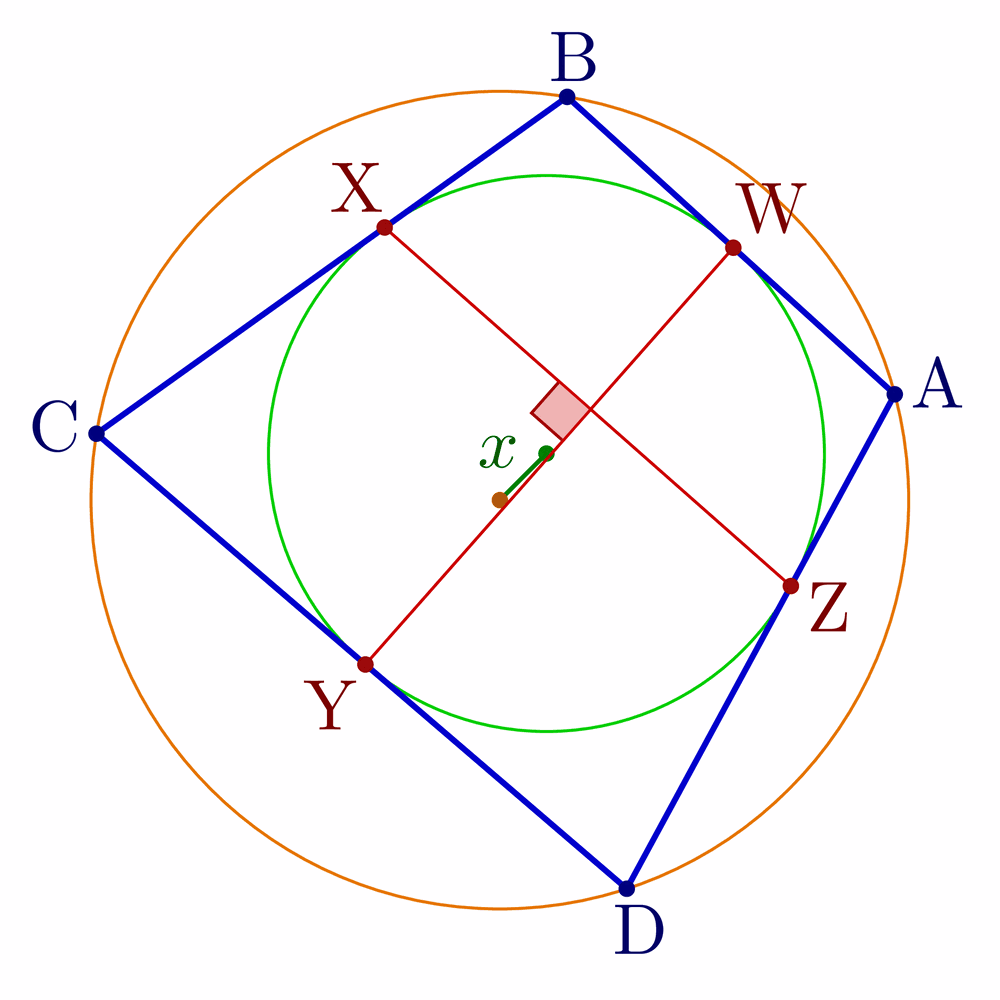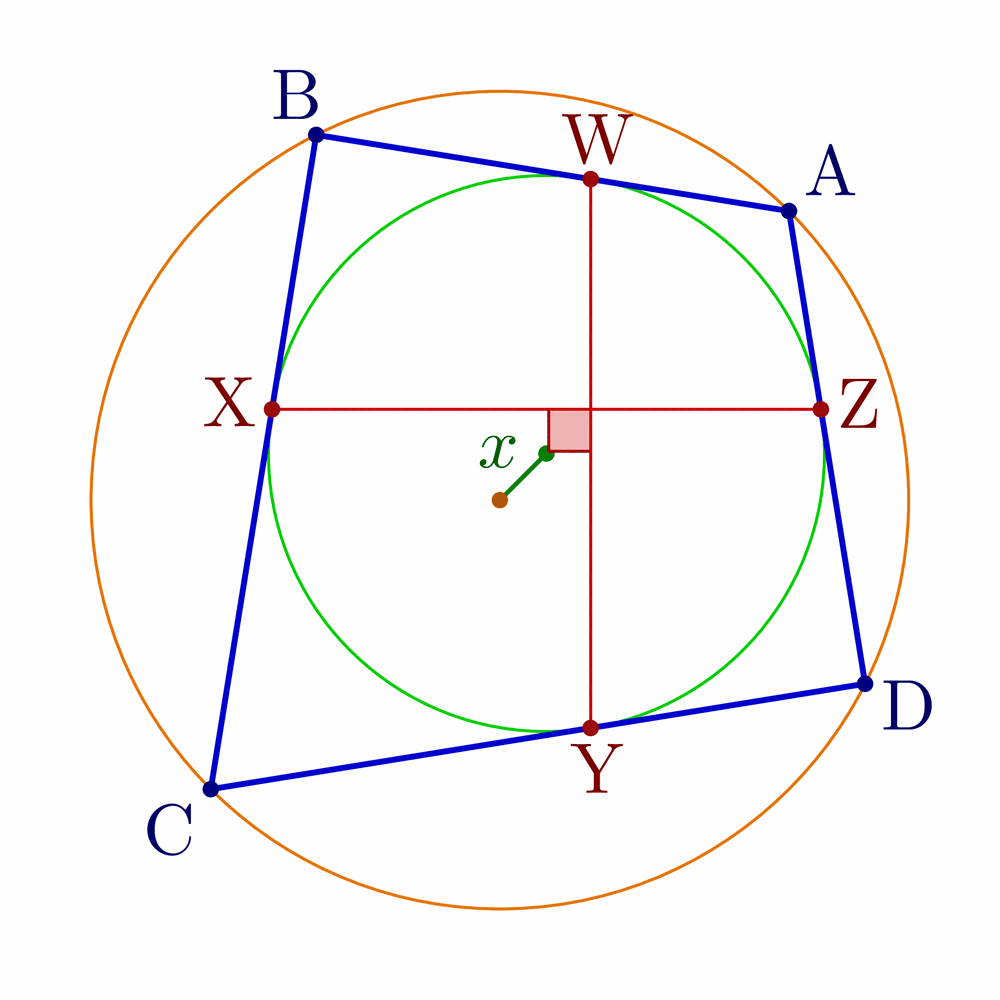
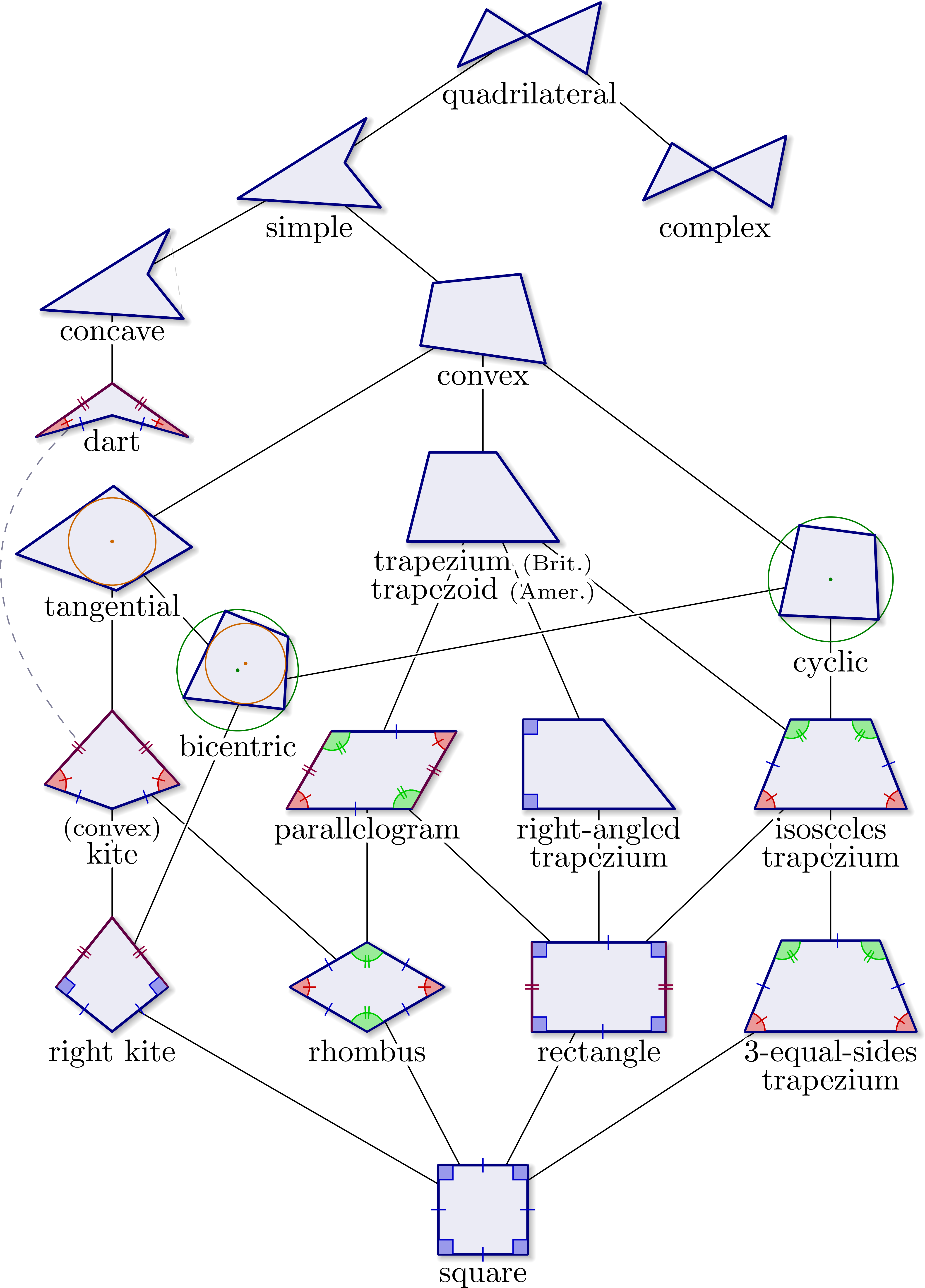
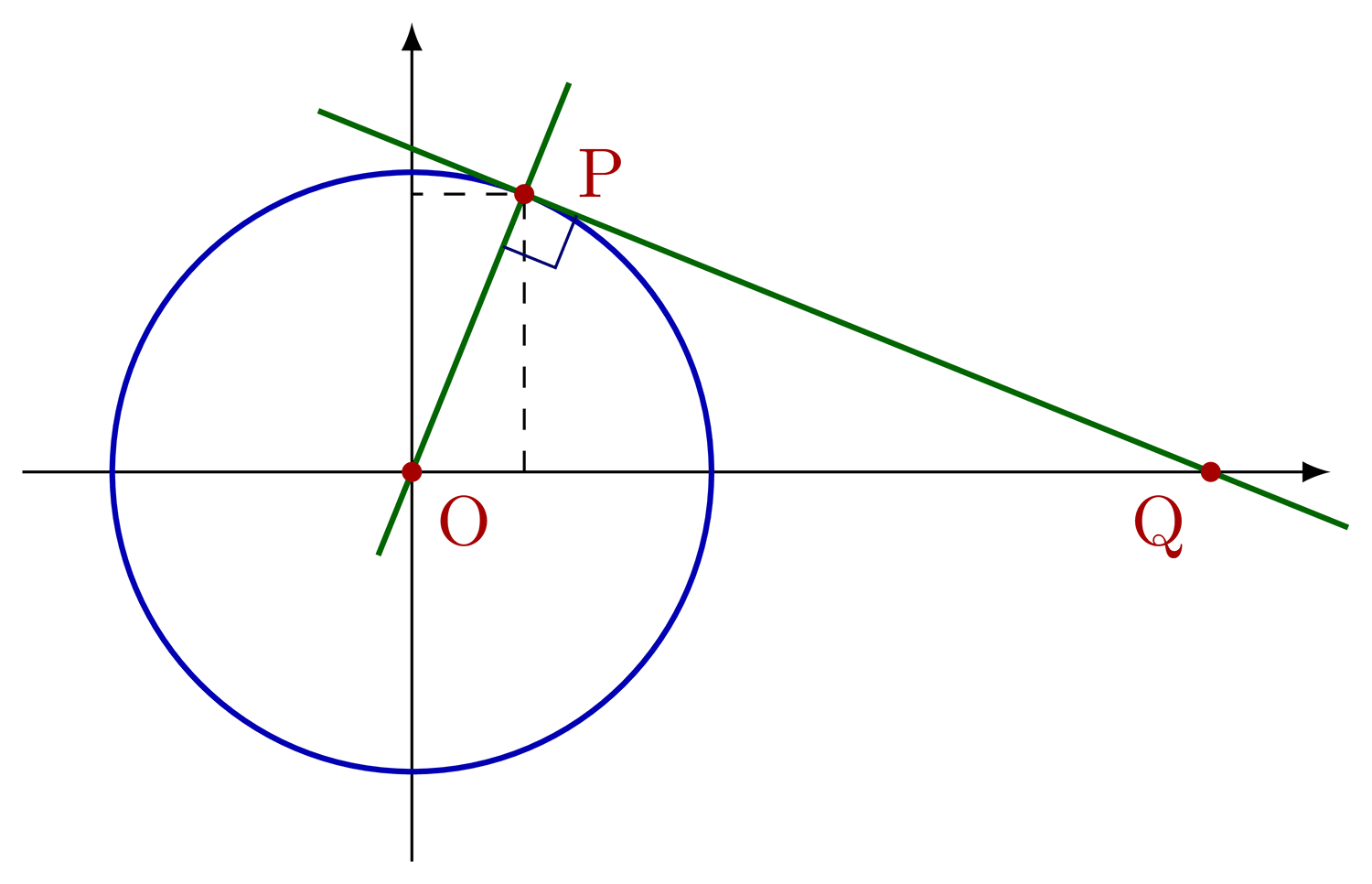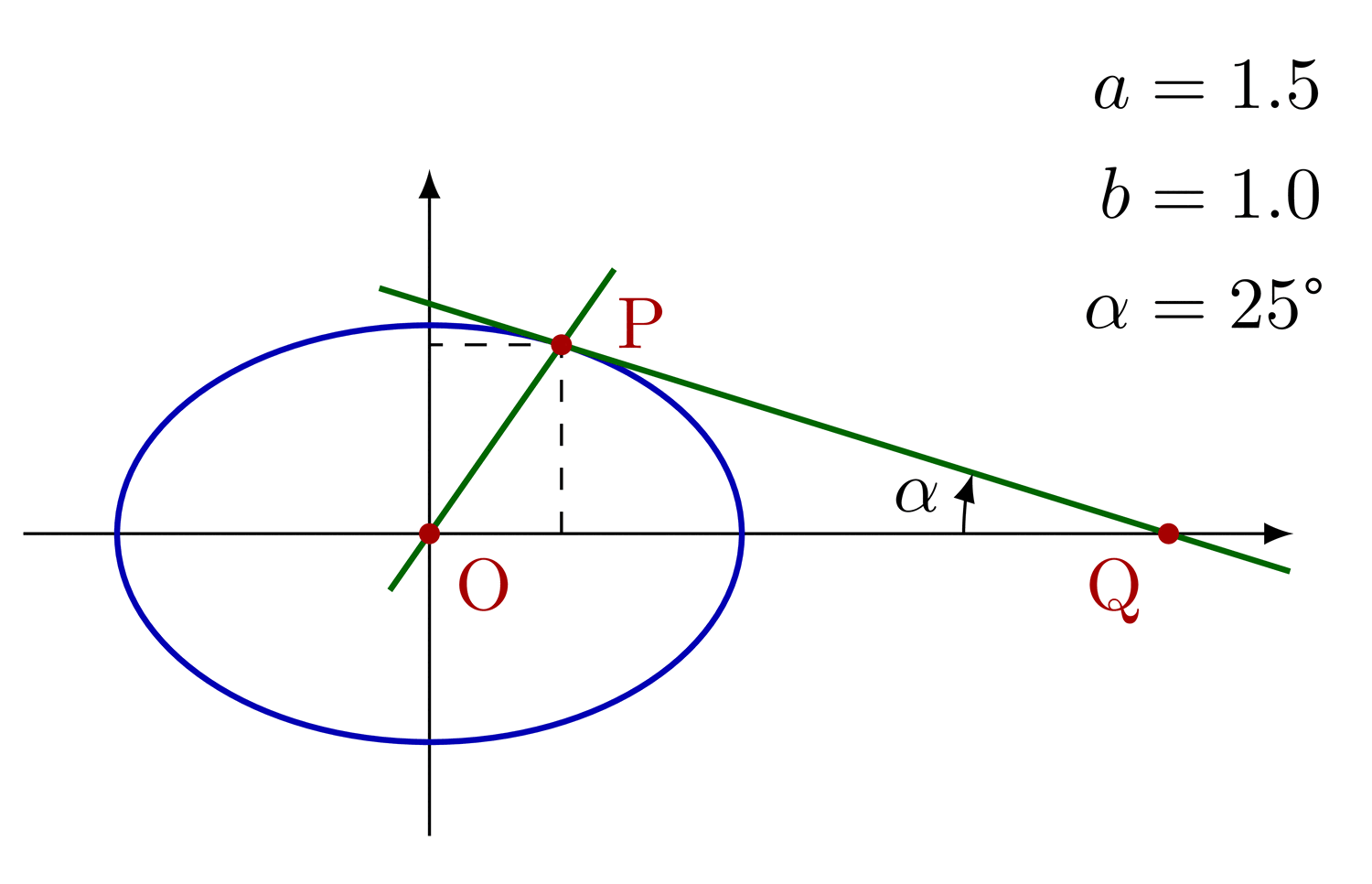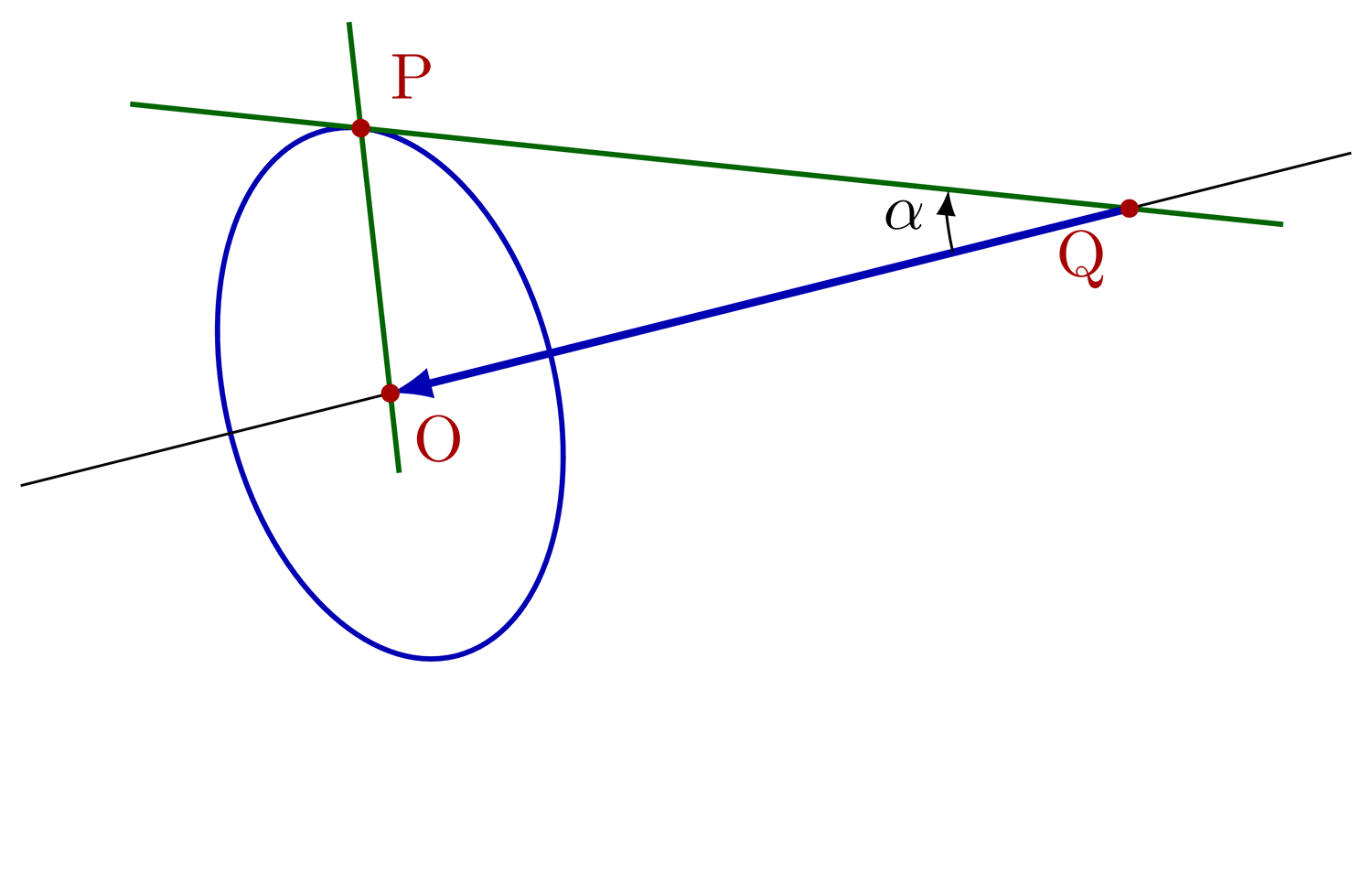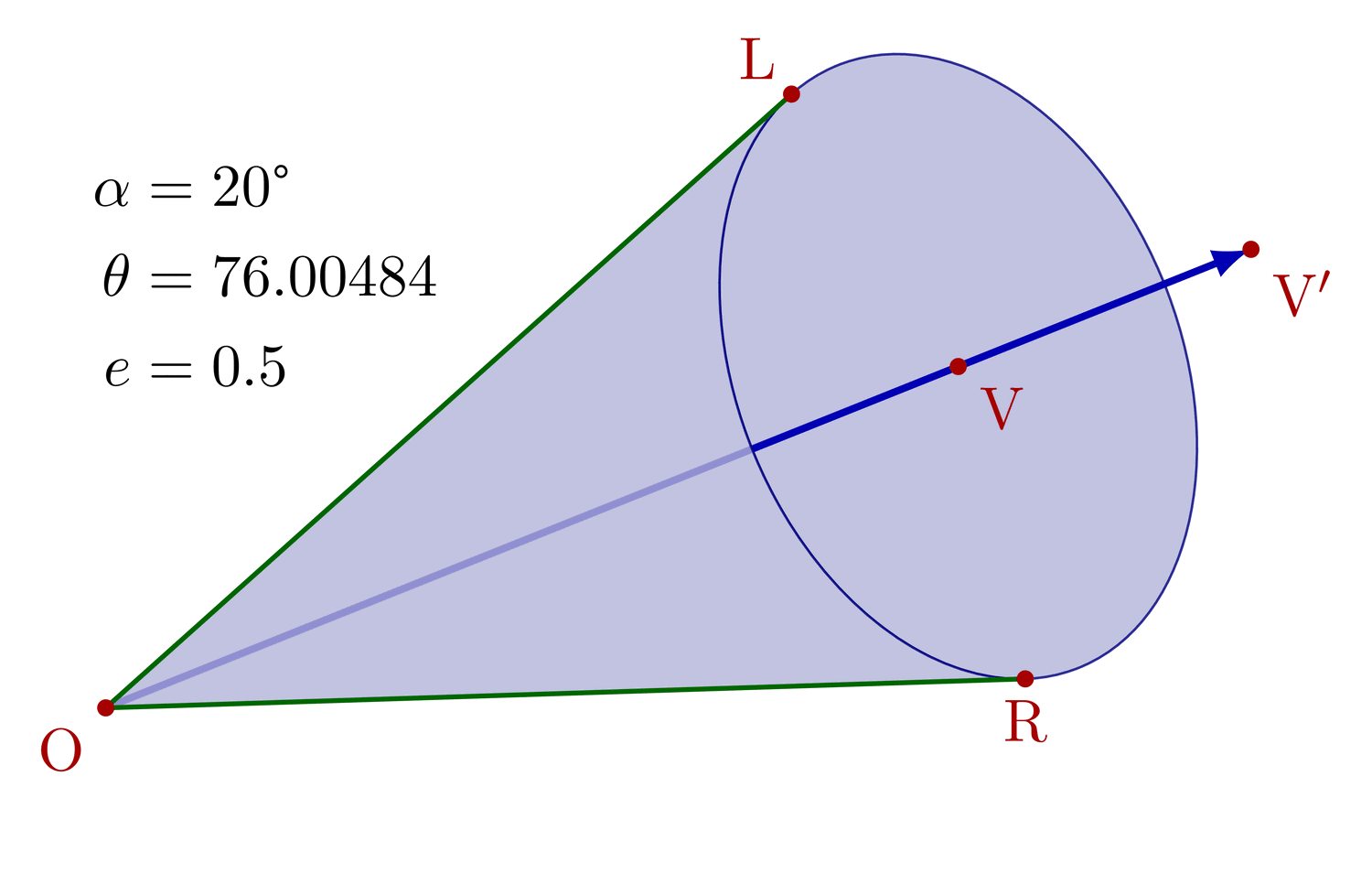
Construct tangential, cyclic and bicentric quadrilaterals.
Bicentric quadrilaterals using intersections:

Edit and compile if you like:
% Author: Izaak Neutelings (January 2022)
\documentclass[border=3pt,tikz]{standalone}
\usetikzlibrary{calc}
\usetikzlibrary{intersections}
\usepackage[outline]{contour} % glow around text
\contourlength{0.9pt}
\colorlet{myred}{red!80!black}
\colorlet{myblue}{blue!80!black}
\colorlet{mygreen}{green!80!black}
\colorlet{myorange}{orange!90!black}
\colorlet{mydarkred}{red!60!black}
\colorlet{mydarkblue}{blue!50!black}
\colorlet{mydarkgreen}{green!50!black}
\colorlet{mydarkorange}{orange!70!black}
\newcommand\rightAngle[4]{
\pgfmathanglebetweenpoints{\pgfpointanchor{#2}{center}}{\pgfpointanchor{#1}{center}}
\coordinate (tmpRA) at ($(#2)+(\pgfmathresult+45:#4)$);
\draw[mydarkblue] ($(#2)!(tmpRA)!(#1)$) -- (tmpRA) -- ($(#2)!(tmpRA)!(#3)$);
}
\tikzset{
angshift/.initial=1, % shift from origin/center
angcol/.style={draw=#1!80!black,fill=#1!30}, % shorthand to fill (light) & draw (dark)
angcol/.default={myblue},
pics/right angle/.style args={(#1)-(#2)-(#3):#4}{ % right angle
code={
\tikzset{angshift/.get=\angshift}
\pgfmathanglebetweenpoints{\pgfpointanchor{#2}{center}}{\pgfpointanchor{#1}{center}}
\pgfmathsetmacro\tmpAngA{\pgfmathresult}
\coordinate (tmpS) at (\tmpAngA+45:\angshift*0.01); % shift
\coordinate (tmp#1) at ($(#1)+(tmpS)$);
\coordinate (tmp#2) at ($(#2)+(tmpS)$);
\coordinate (tmp#3) at ($(#3)+(tmpS)$);
\coordinate (tmpRA) at ($(tmp#2)+(\tmpAngA+45:#4)$);
\fill[pic actions,draw=none] % fill square area
($(tmp#2)!(tmpRA)!(tmp#1)$) -- (tmpRA) -- ($(tmp#2)!(tmpRA)!(tmp#3)$) -- (tmp#2) -- cycle;
\draw[pic actions,fill=none] % draw orthogonal mark
($(tmp#2)!(tmpRA)!(tmp#1)$) -- (tmpRA) -- ($(tmp#2)!(tmpRA)!(tmp#3)$);
}
}
}
\begin{document}
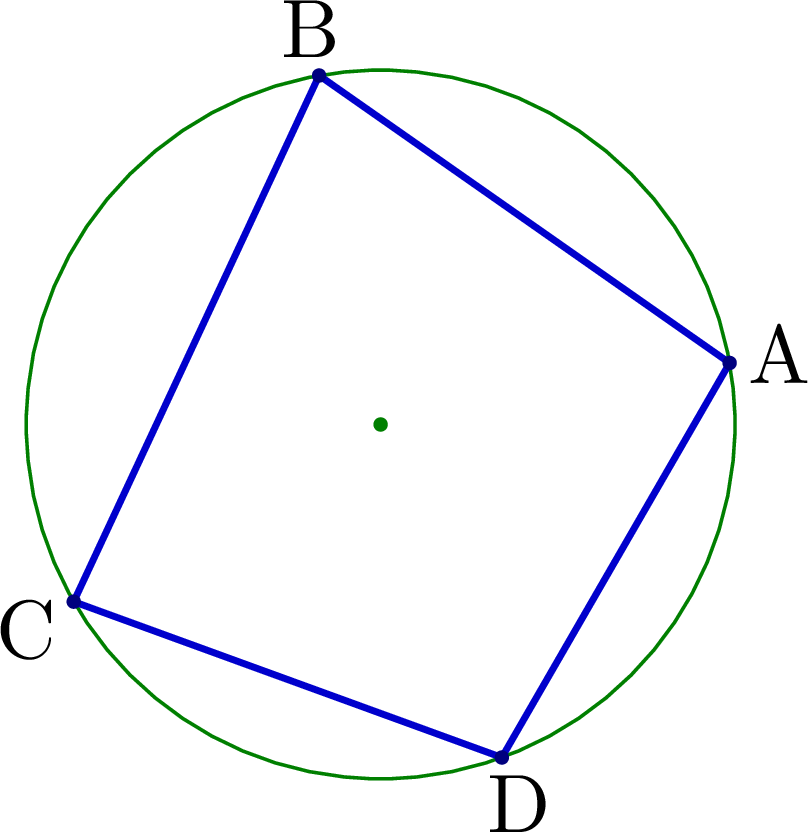
% CYCLIC QUADRILATERAL
% Construct cyclic quadrilateral four points on the circumcircle
\begin{tikzpicture}[scale=1.5]
\def\R{1.0} % circumradius = radius of circumcircle
% COORDINATES
\coordinate (O) at (0,0);
%\coordinate (A) at ( 10:\R);
%\coordinate (B) at (100:\R);
%\coordinate (C) at (210:\R);
%\coordinate (D) at (290:\R);
\foreach \P/\angP in {A/10,B/100,C/210,D/290}{
\coordinate (\P) at (\angP:\R); % vertex
\node[anchor=180+\angP,inner sep=2] at (\P) {\P};
}
% LINES
\draw[mydarkgreen] (O) circle(\R);
\draw[myblue,thick] (A) -- (B) -- (C) -- (D) -- cycle;
\fill[mydarkgreen] (O) circle(0.02);
\fill[mydarkblue]
(A) circle(0.02) (B) circle(0.02)
(C) circle(0.02) (D) circle(0.02);
\end{tikzpicture}
% TANGENTIAL TRAPEZOID
% Construct tangential trapezoid from four points of tangency on the incircle
\begin{tikzpicture}[scale=1.5]
\def\R{1.0} % inradius = radius of incircle
\def\angW{5} % polar angle of tangent point W
% CIRCLE
\coordinate (O) at (0,0);
\draw[mydarkgreen] (O) circle(\R);
% COORDINATES
\foreach \P/\Q/\angQ [remember={\angQ as \lastang (initially \angW);},
evaluate={
\r=\R/cos((\angQ-\lastang)/2);
\angP=(\angQ+\lastang)/2;
}] in {A/X/98,B/Y/210,C/Z/290,D/W/\angW}{
\coordinate (\P) at (\angP:\r); % vertex
\coordinate (\Q) at (\angQ:\R); % point of tangency
\node[anchor=180+\angP,inner sep=2] at (\P) {\P};
\node[anchor=180+\angQ,inner sep=2] at (\Q) {\Q};
}
% LINES
\draw[myblue,thick] (A) -- (B) -- (C) -- (D) -- cycle;
\draw[myred] (X) -- (Z) (W) -- (Y);
\fill[mydarkgreen] (O) circle(0.02);
\fill[mydarkblue]
(A) circle(0.02) (B) circle(0.02)
(C) circle(0.02) (D) circle(0.02);
\fill[mydarkred]
(W) circle(0.02) (X) circle(0.02)
(Y) circle(0.02) (Z) circle(0.02);
\end{tikzpicture}
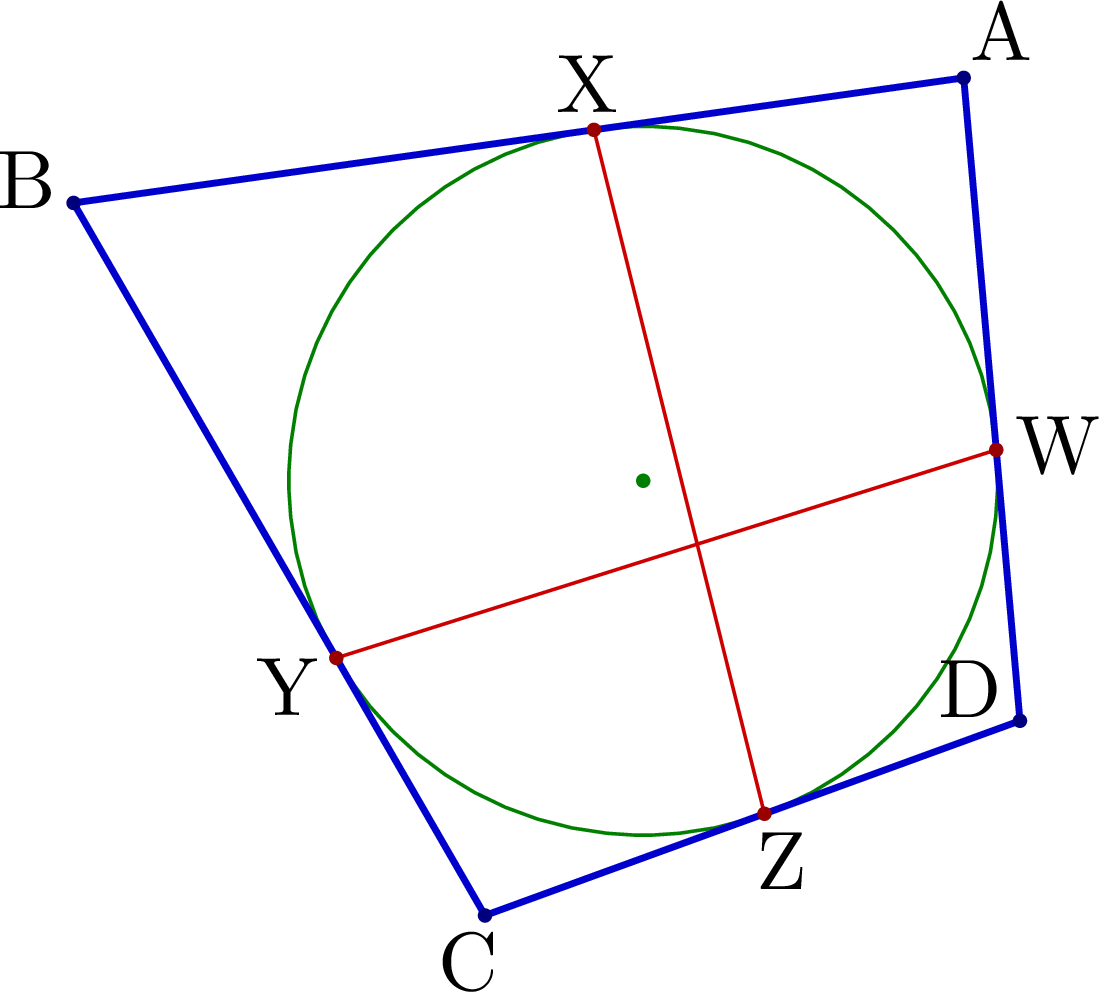
% TANGENTIAL TRAPEZOID using intersections
% Construct tangential trapezoid from four points of tangency on the incircle using intersections
\begin{tikzpicture}[scale=2]
% CIRCLE
\def\R{1} % inradius = radius of incircle
\coordinate (O) at (0,0);
\draw[mydarkgreen] (O) circle(\R);
% COORDINATES
\foreach \Q/\angQ in {W/10,X/95,Y/210,Z/290}{
\coordinate (\Q) at (\angQ:\R); % vertex
\node[anchor=180+\angQ,inner sep=2] at (\Q) {\Q};
}
% TANGENTS & INTERSECTIONS
\draw[myblue,thick,name path=W] ($(W)!1.5!90:(O)$) -- (W) -- ($(W)!1.5!-90:(O)$);
\draw[myblue,thick,name path=X] ($(X)!1.5!90:(O)$) -- (X) -- ($(X)!1.9!-90:(O)$);
\draw[myblue,thick,name path=Y] ($(Y)!1.9!90:(O)$) -- (Y) -- ($(Y)!1.5!-90:(O)$);
\draw[myblue,thick,name path=Z] ($(Z)!1.5!90:(O)$) -- (Z) -- ($(Z)!1.5!-90:(O)$);
\path[name intersections={of={W and X},by=A}] node at ($(A)+(O)!5pt!(A)$) {A};
\path[name intersections={of={X and Y},by=B}] node at ($(B)+(O)!5pt!(B)$) {B};
\path[name intersections={of={Y and Z},by=C}] node at ($(C)+(O)!5pt!(C)$) {C};
\path[name intersections={of={Z and W},by=D}] node at ($(D)+(O)!5pt!(D)$) {D};
% LINES
\draw[myblue,thick] (A) -- (B) -- (C) -- (D) -- cycle;
\draw[myred] (X) -- (Z) (W) -- (Y);
\fill[mydarkgreen] (O) circle(0.02);
\fill[mydarkblue]
(A) circle(0.02) (B) circle(0.02)
(C) circle(0.02) (D) circle(0.02);
\fill[mydarkred]
(W) circle(0.02) (X) circle(0.02)
(Y) circle(0.02) (Z) circle(0.02);
\end{tikzpicture}
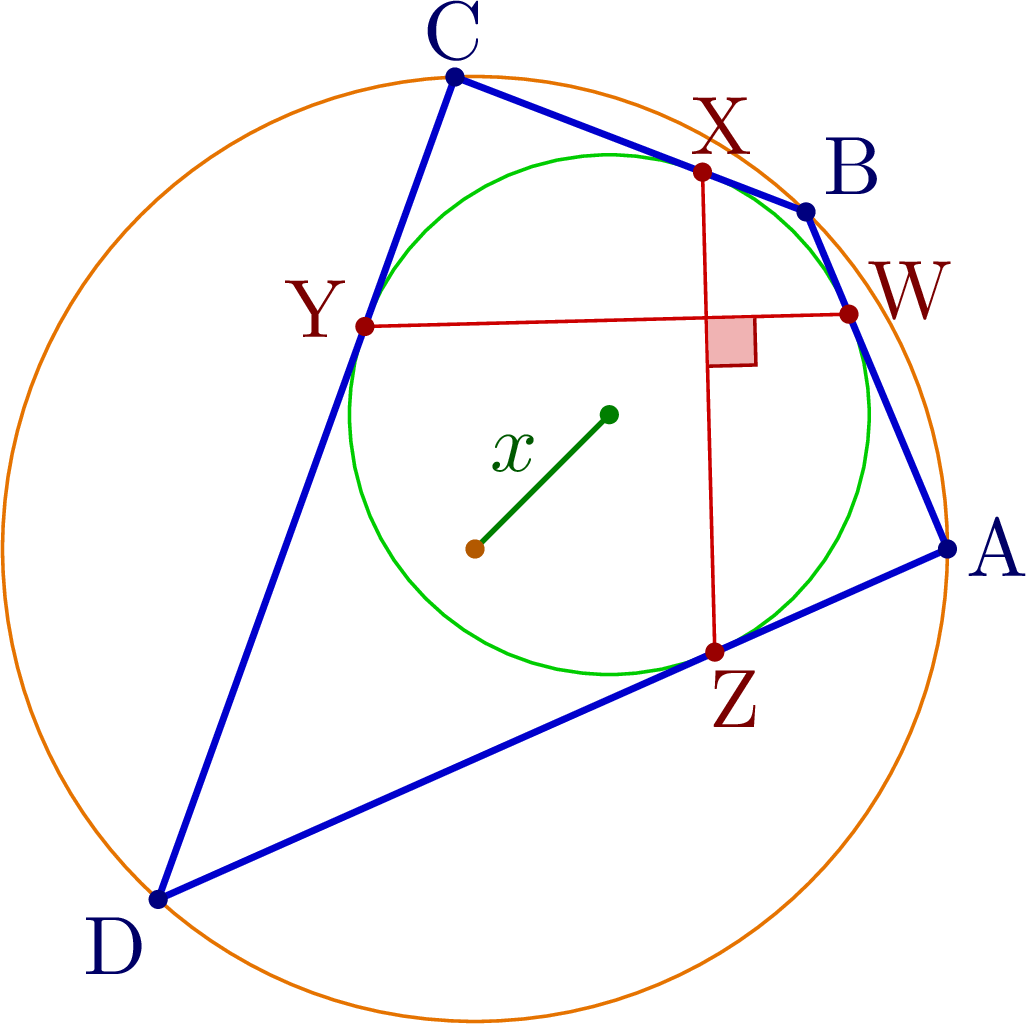
% BICENTRIC QUADRILATERAL
% http://dynamicmathematicslearning.com/new-bicentric-construction.html
% Construct bicentric quadrilateral for given incircle, circumcircle and one vertex
\foreach \r in {0.55,0.68}{ % inradius = radius of incircle
\foreach \angA in {0,20,45}{ % polar angle of point A
%\foreach \angA in {0,10,15,20,25,30,35,40,45,50}{ % polar angle of point A
\begin{tikzpicture}[scale=2.0]
%\def\r{0.68} % inradius = radius of incircle
\def\R{1.0} % circumradius = radius of circumcircle
\def\angXi{45} % polar angle of incircle center
%\def\angA{15} % polar angle of point A
\pgfmathsetmacro\x{sqrt(\R^2+\r^2-\r*sqrt(4*\R^2+\r^2))} % Fuss's theorem
% CIRCLES
\coordinate (Oout) at (0,0);
\coordinate (Oin) at (\angXi:\x);
\draw[mydarkgreen,line width=0.6] (Oout) -- (Oin)
node[mydarkgreen!70!black,midway,anchor=\angXi-90,inner sep=1] {$x$};
\fill[mydarkgreen] (Oin) circle(0.02);
\fill[mydarkorange] (Oout) circle(0.02);
\draw[mygreen] (Oin) circle(\r);
\draw[myorange] (Oout) circle(\R);
% COORDINATES
\foreach \P/\Q [
remember={\angP as \lastang (initially \angA);},
evaluate={
\d=sqrt(\x^2+\R^2-\r^2-2*\x*\R*cos(\angXi-\lastang));
\D=sqrt(\d^2+\r^2); %sqrt(\x^2+\R^2-2*\x*\R*cos(\angXi-\lastang));
\tanang=90+atan2(\d,\r)+atan2(\R*sin(\lastang)-\x*sin(\angXi),\R*cos(\lastang)-\x*cos(\angXi));
\angP=2*\tanang-\lastang-180;
}] in {B/W,C/X,D/Y,A/Z}{
\coordinate (\P) at (\angP:\R); % corner
\coordinate (\Q) at ($(\lastang:\R)+(\tanang:\d)$); % point of tangency
\node[mydarkblue!80!black,anchor=180+\angP,inner sep=2] at (\P) {\P};
\node[mydarkred!80!black,anchor=90+\tanang,inner sep=2] at (\Q) {\Q};
}
\coordinate (A) at (\angA:\R); % overwrite for precision
% SIDES
\draw[myblue,thick] (A) -- (B) -- (C) -- (D) -- cycle;
\draw[myred,name path=a] (X) -- (Z);
\draw[myred,name path=b] (W) -- (Y);
\fill[mydarkblue]
(A) circle(0.02) (B) circle(0.02)
(C) circle(0.02) (D) circle(0.02);
\fill[mydarkred]
(W) circle(0.02) (X) circle(0.02)
(Y) circle(0.02) (Z) circle(0.02);
\path[name intersections={of={a and b},by=O}]; % get intersection C
%\rightAngle{Z}{C}{W}{0.15} % mark right angle
\pic[angcol=myred] {right angle={(Z)-(O)-(W):0.28}};
%\pic[angcol=myred] {right angle={(X)-(O)-(Y):0.28}};
\end{tikzpicture}
}
}
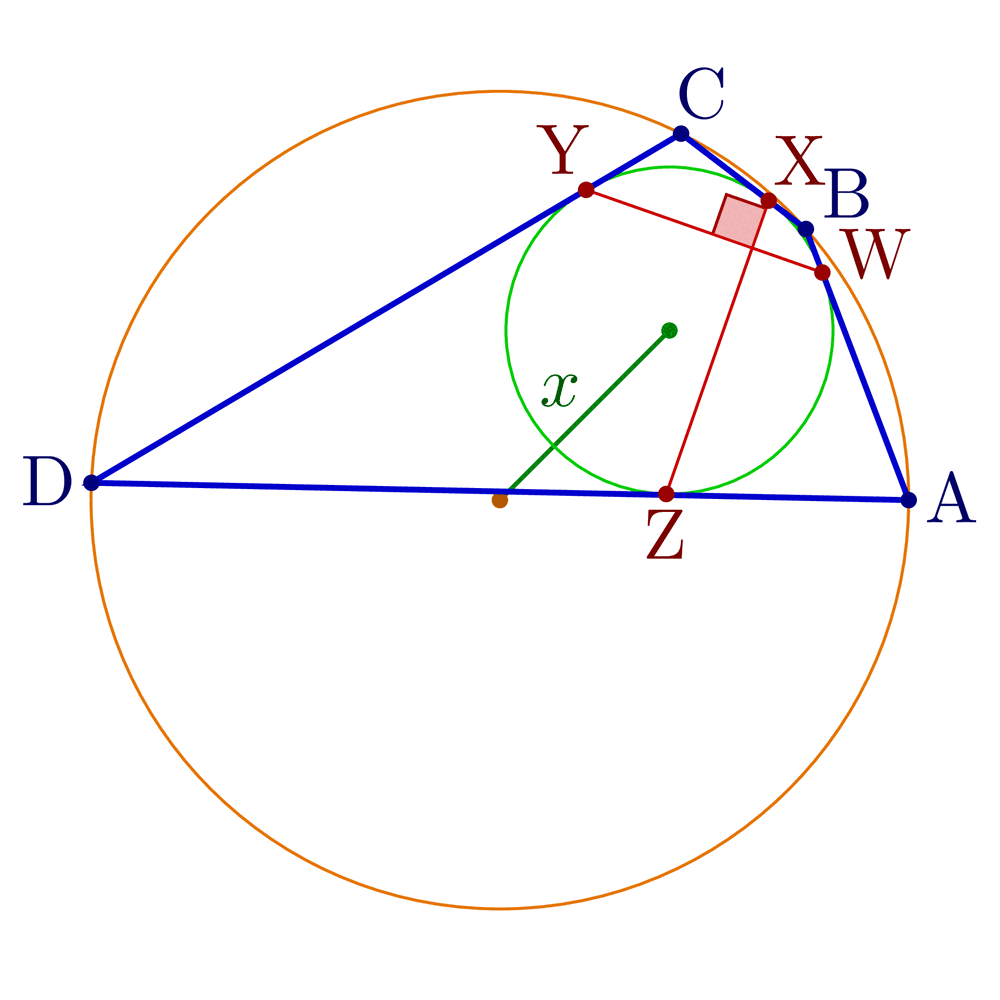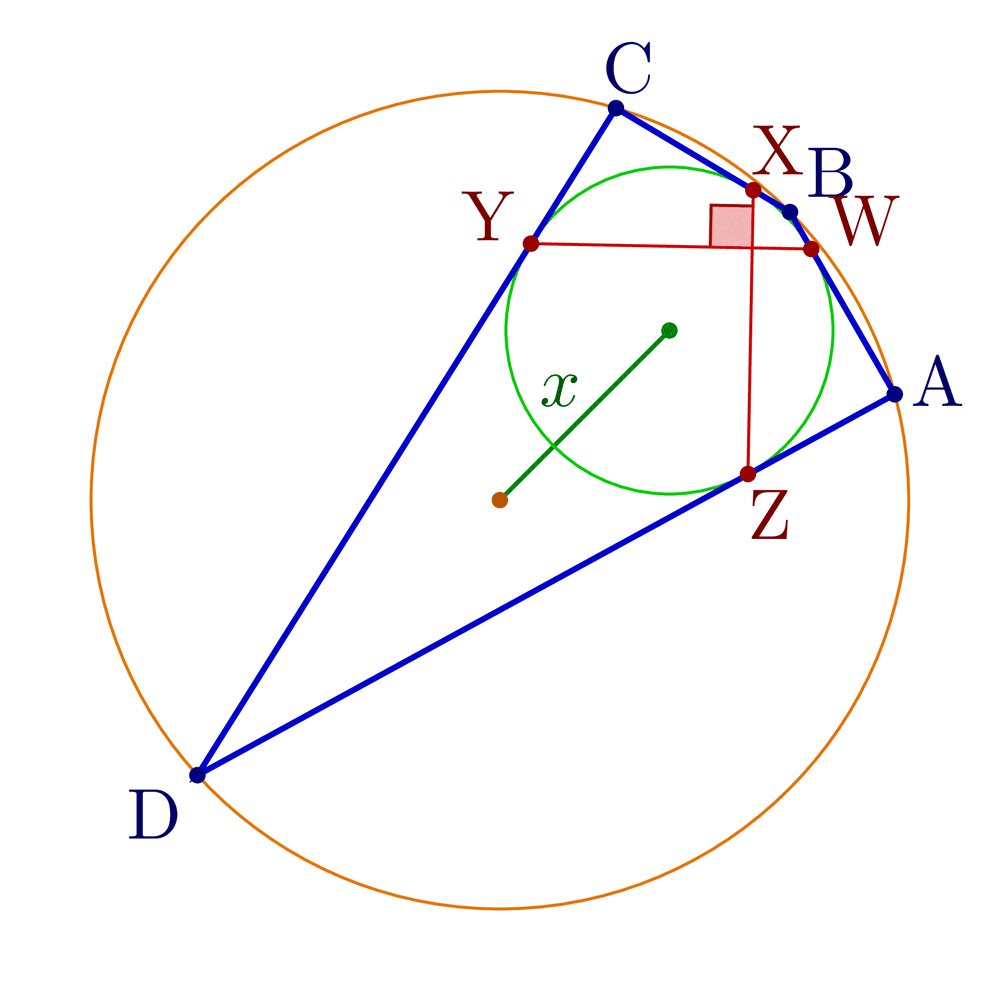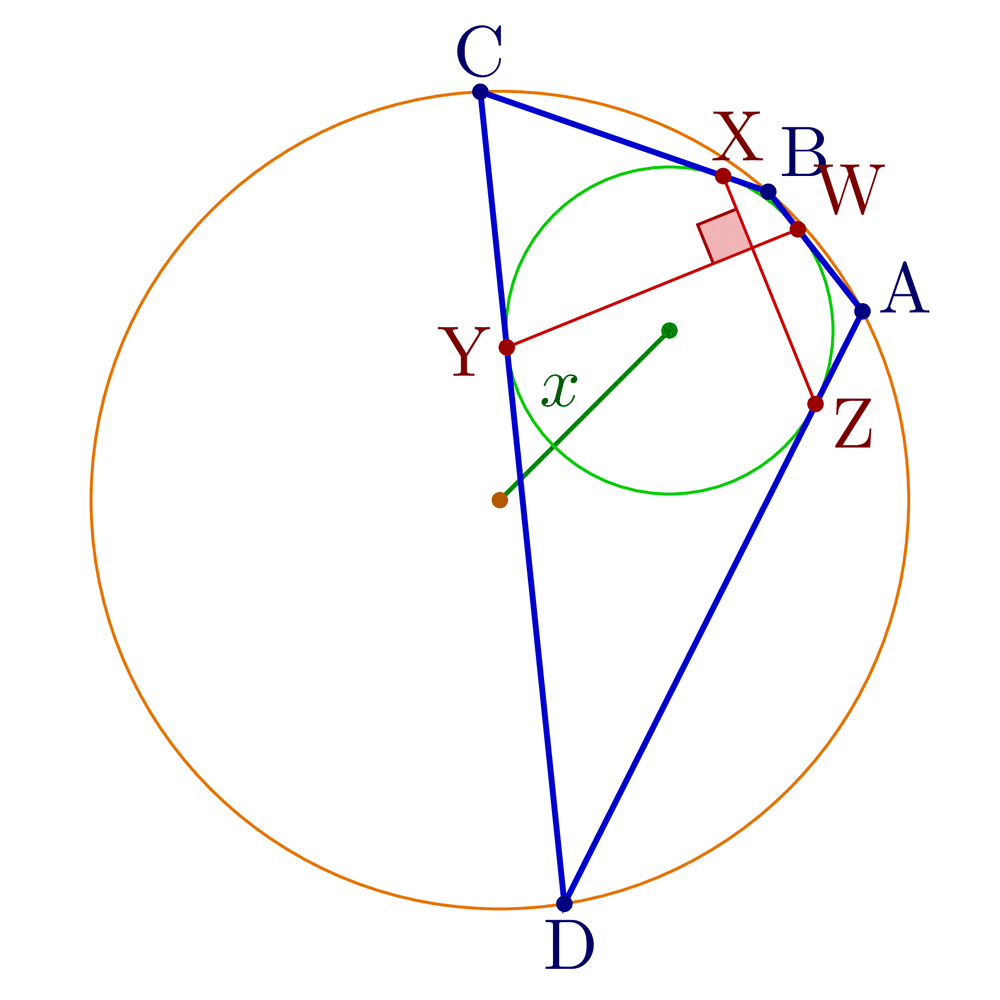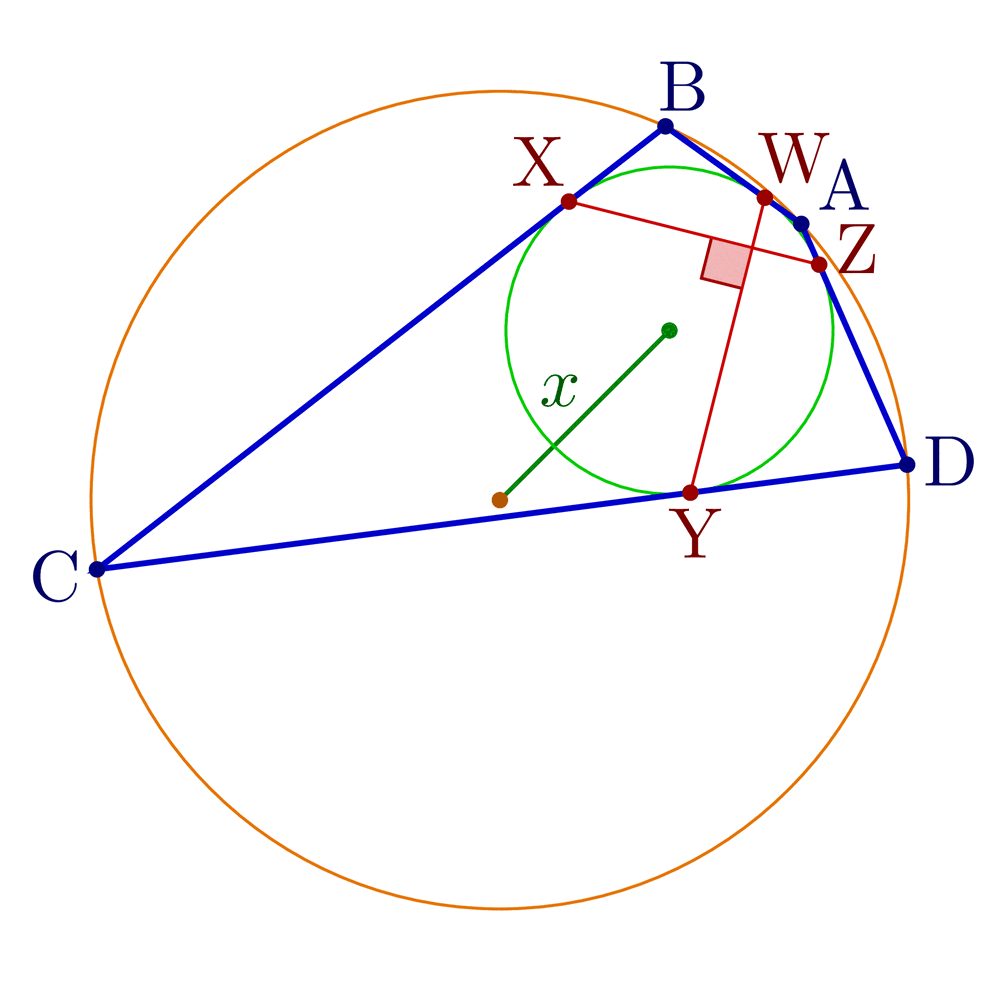
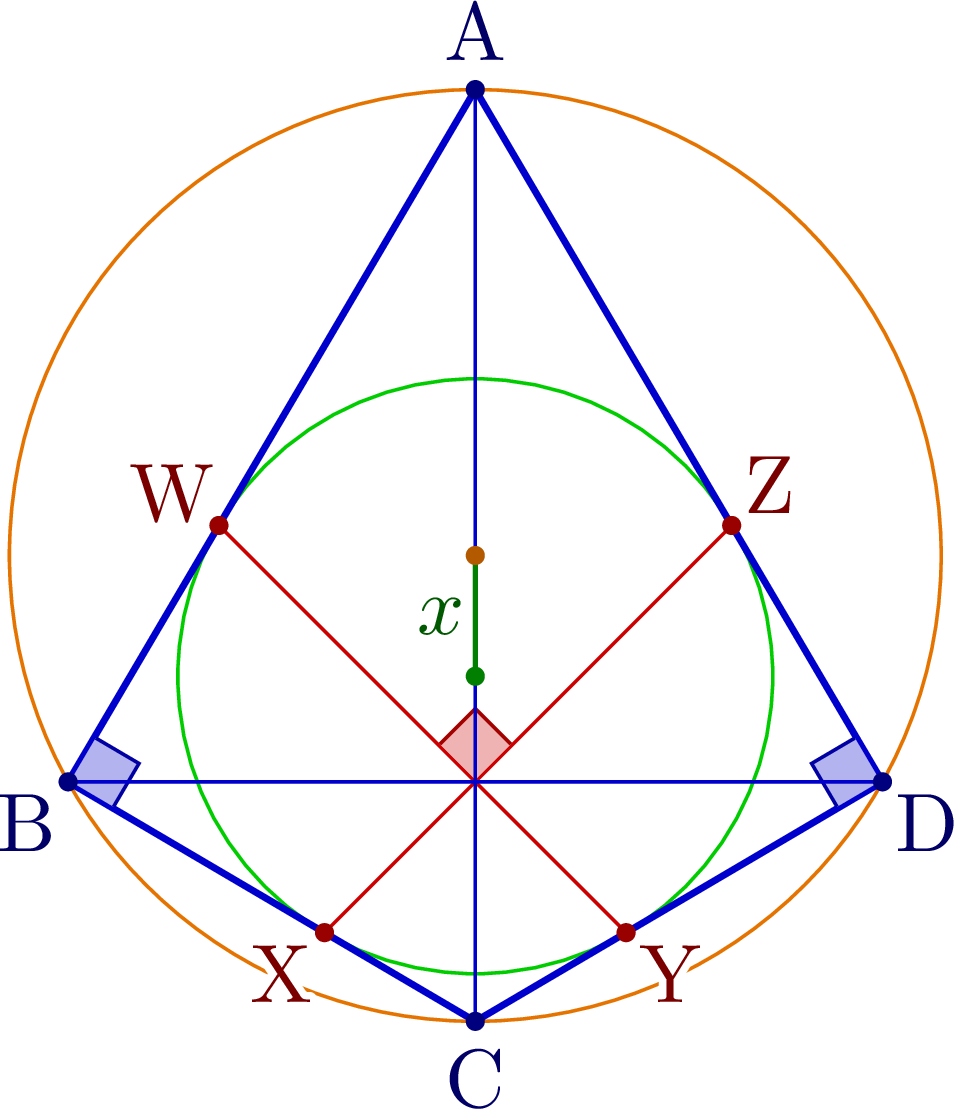
% BICENTRIC QUADRILATERAL - right kite
% https://en.wikipedia.org/wiki/Right_kite
\begin{tikzpicture}[scale=2.0]
\def\a{1.7} % length of long sides
\def\b{1.0} % length of short sides
\pgfmathsetmacro\angA{2*atan2(\b,\a)} % angle A = B--A--D
\pgfmathsetmacro\angC{180-\angA} % angle C = B--C--D
\pgfmathsetmacro\R{sqrt(\a^2+\b^2)/2} % circumradius = radius of circumcircle
\pgfmathsetmacro\r{\a*\b/(\a+\b)} % inradius = radius of incircle
\pgfmathsetmacro\R{sqrt(\a^2+\b^2)/2} % Fuss's theorem
\pgfmathsetmacro\x{sqrt(\R^2+\r^2-\r*sqrt(4*\R^2+\r^2))} % Fuss's theorem
% COORDINATES
\coordinate (Oout) at (0,0);
\coordinate (Oin) at (-90:\x);
\coordinate (A) at (90:\R);
\coordinate (B) at (270-\angA:\R);
\coordinate (C) at (-90:\R);
\coordinate (D) at (\angA-90:\R);
\coordinate (W) at ($(Oin)+(180-\angA/2:\r)$);
\coordinate (X) at ($(Oin)+(180+\angC/2:\r)$);
\coordinate (Y) at ($(Oin)+(-\angC/2:\r)$);
\coordinate (Z) at ($(Oin)+(\angA/2:\r)$);
% CIRCLES
\draw[mygreen] (Oin) circle(\r);
\draw[myorange] (Oout) circle(\R);
% SIDES
\draw[myblue,thick] (A) -- (B) -- (C) -- (D) -- cycle;
\draw[myred,name path=a] (X) -- (Z);
\draw[myred,name path=b] (W) -- (Y);
% MARK ANGLES
\path[name intersections={of={a and b},by=O}]; % get intersection O
%\rightAngle{Z}{C}{W}{0.15} % mark right angle
%\rightAngle{X}{B}{W}{0.15} % mark right angle
%\rightAngle{Z}{D}{Y}{0.15} % mark right angle
\pic[angcol=myred] {right angle={(Z)-(O)-(W):0.30}};
\pic[angcol=myblue] {right angle={(X)-(B)-(W):0.30}};
\pic[angcol=myblue] {right angle={(Z)-(D)-(Y):0.30}};
\draw[myblue,thin] (A) -- (C) (B) -- (D);
\draw[mydarkgreen,thick,line width=0.6] (Oout) -- (Oin)
node[mydarkgreen!70!black,midway,anchor=0,inner sep=1] {$x$};
% DOTS
\fill[mydarkgreen] (Oin) circle(0.02);
\fill[mydarkorange] (Oout) circle(0.02);
\fill[mydarkblue]
(A) circle(0.02) node[mydarkblue!80!black,above] {A}
(B) circle(0.02) node[mydarkblue!80!black,below left=-2] {B}
(C) circle(0.02) node[mydarkblue!80!black,below] {C}
(D) circle(0.02) node[mydarkblue!80!black,below right=-2] {D};
\fill[mydarkred]
(W) circle(0.02) node[mydarkred!80!black,above left=-3] {W}
(X) circle(0.02) node[mydarkred!80!black,below left=-2] {\contour{white}{X}}
(Y) circle(0.02) node[mydarkred!80!black,below right=-2] {\contour{white}{Y}}
(Z) circle(0.02) node[mydarkred!80!black,above right=-2] {Z};
\end{tikzpicture}
\end{document}
Click to download: quadrilaterals_bicentric.tex • quadrilaterals_bicentric.pdf
Open in Overleaf: quadrilaterals_bicentric.tex