Gravitational force and field

Some diagrams to illustrating Newton’s universal law of gravitation between masses, and the gravitational force field of Earth.
For more related figures, please see the “forces” or “Newton’s laws” tag.

Forces of gravitational attraction:

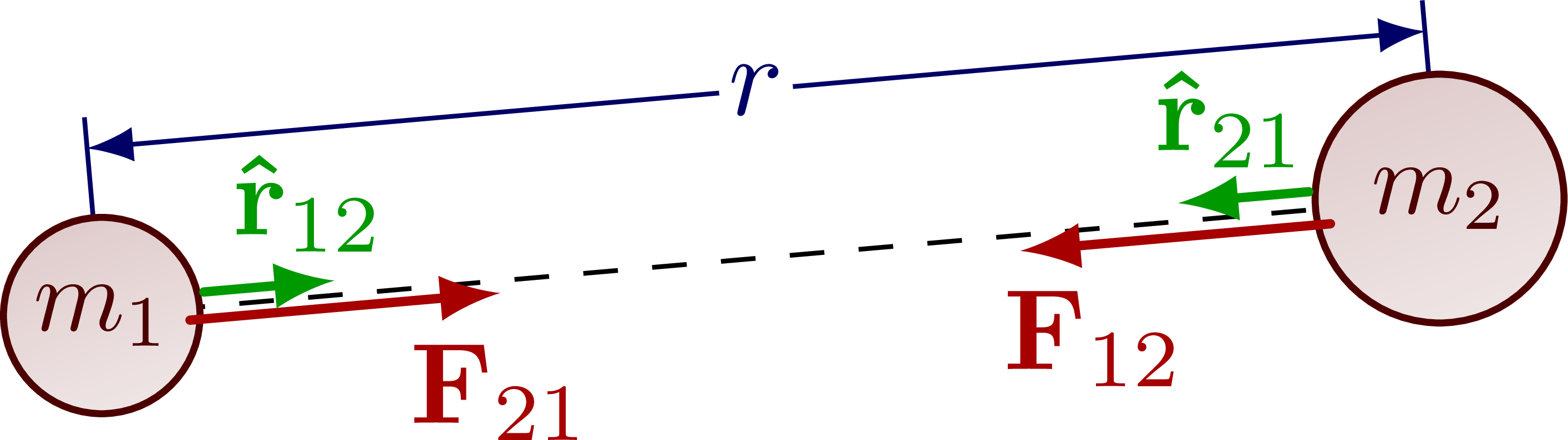
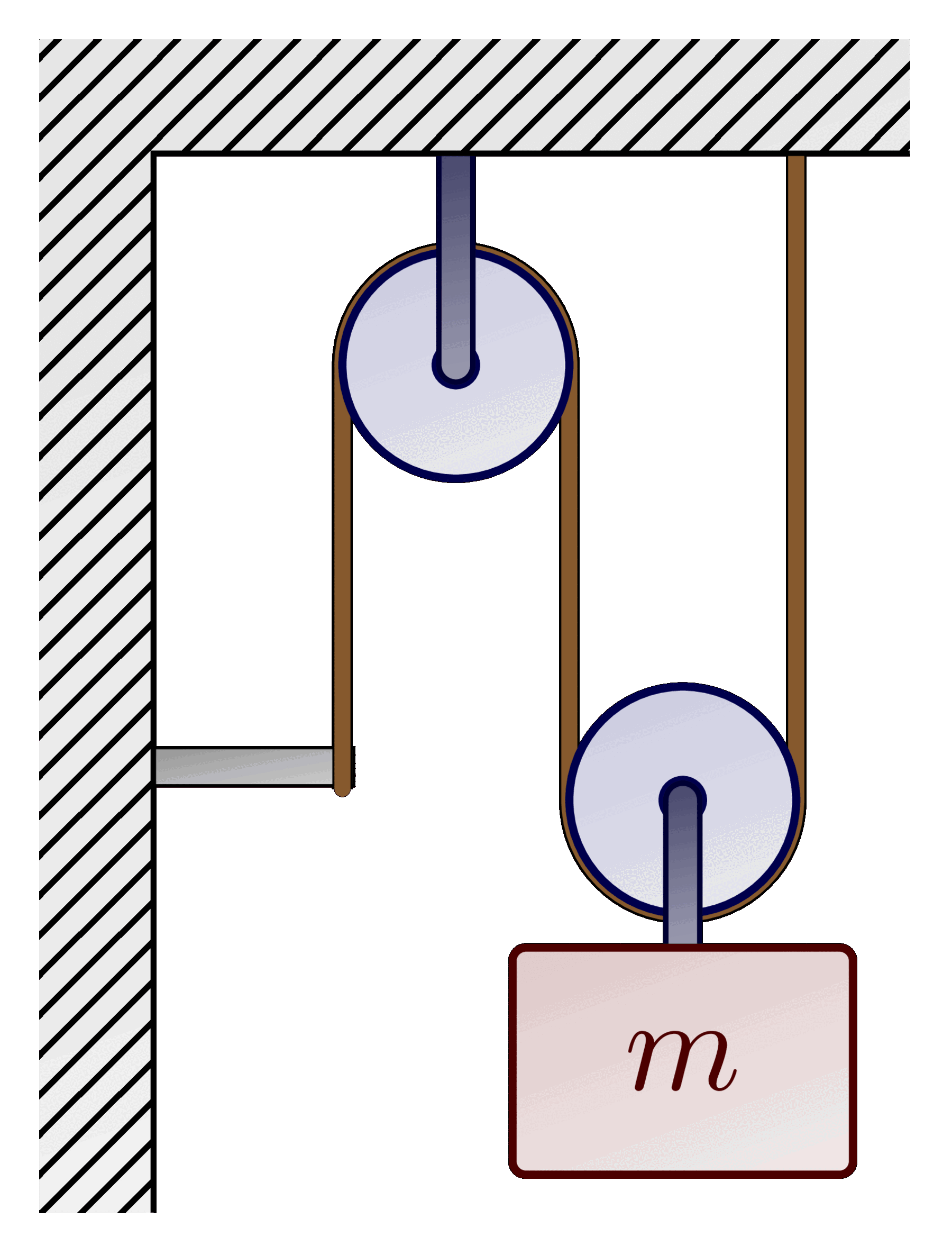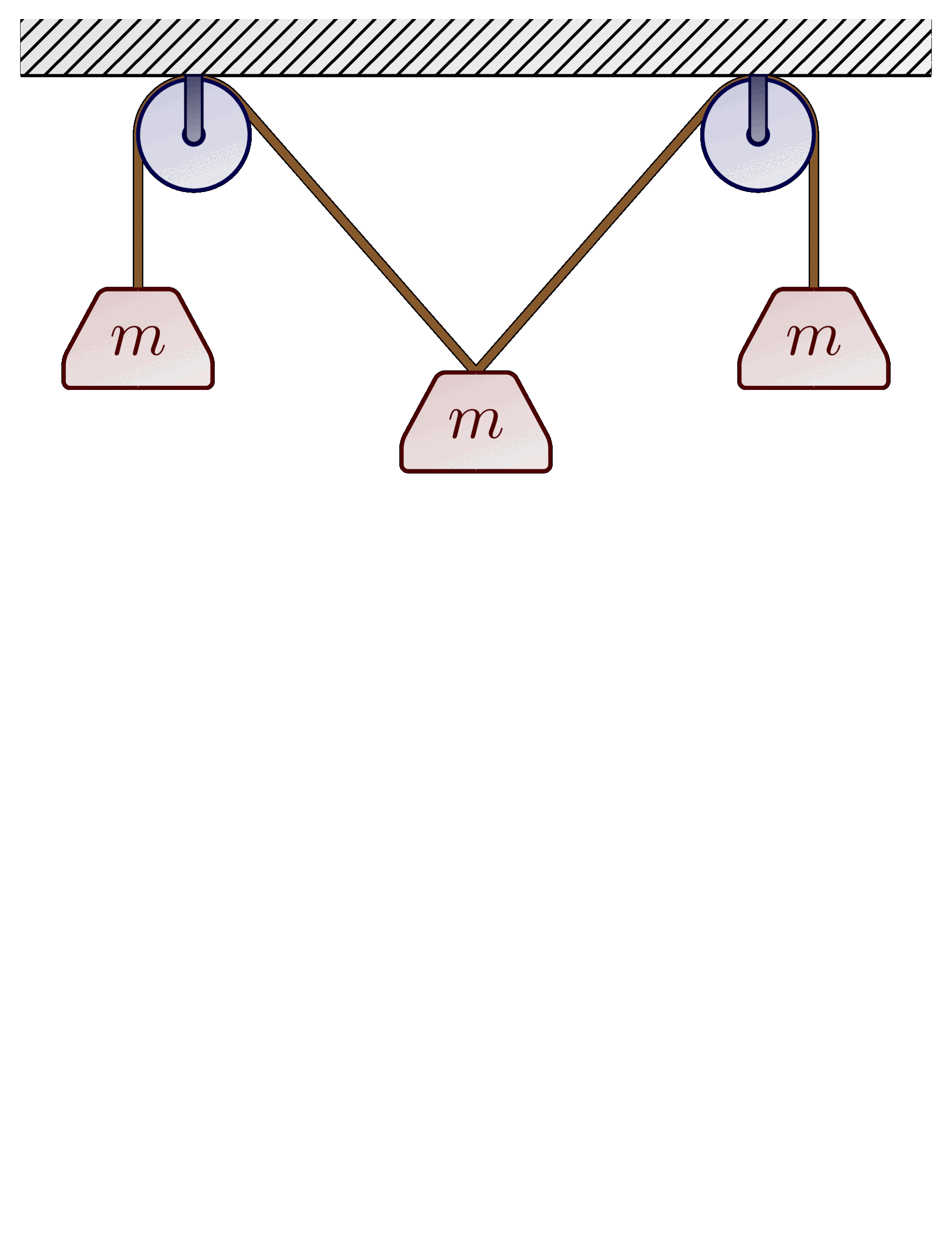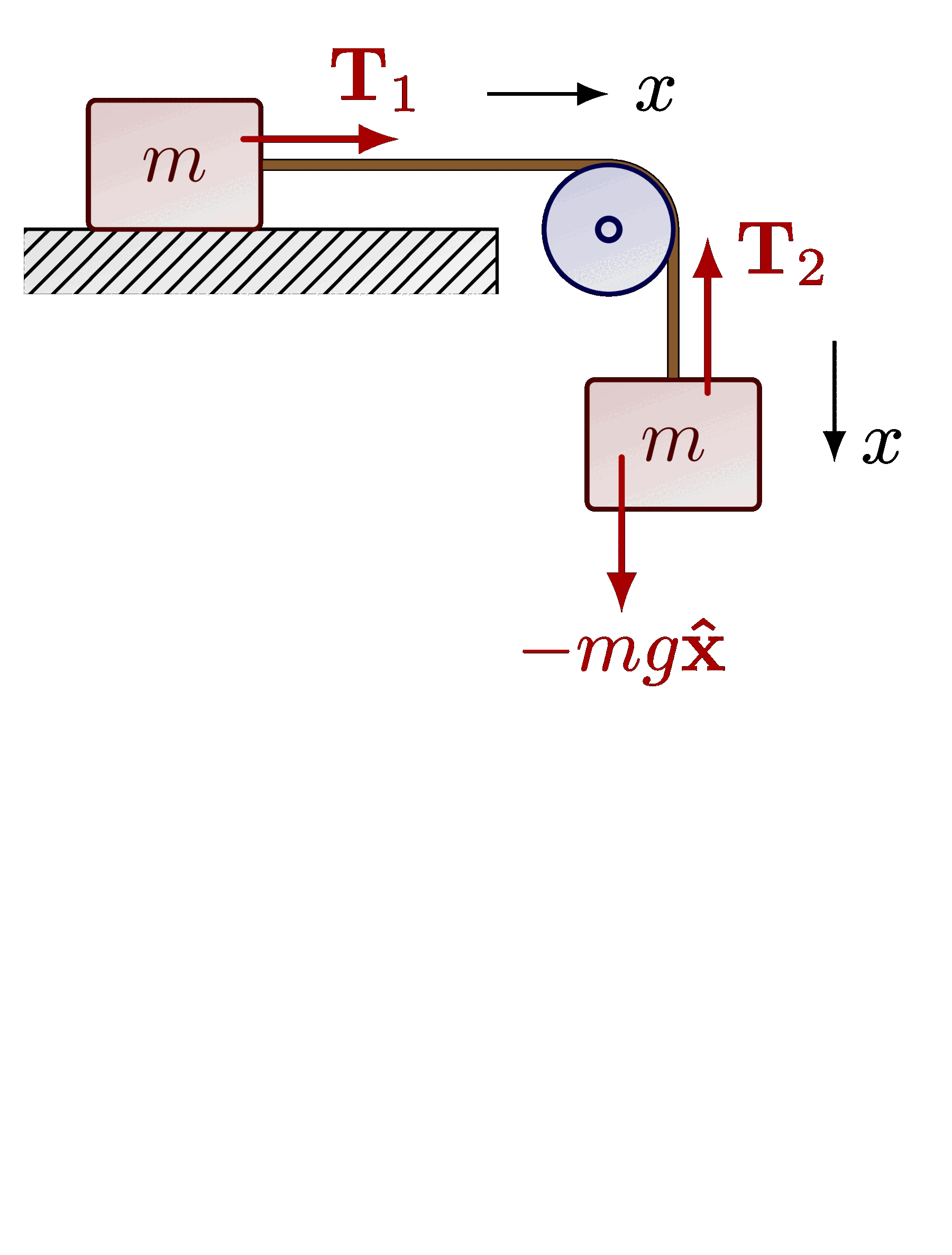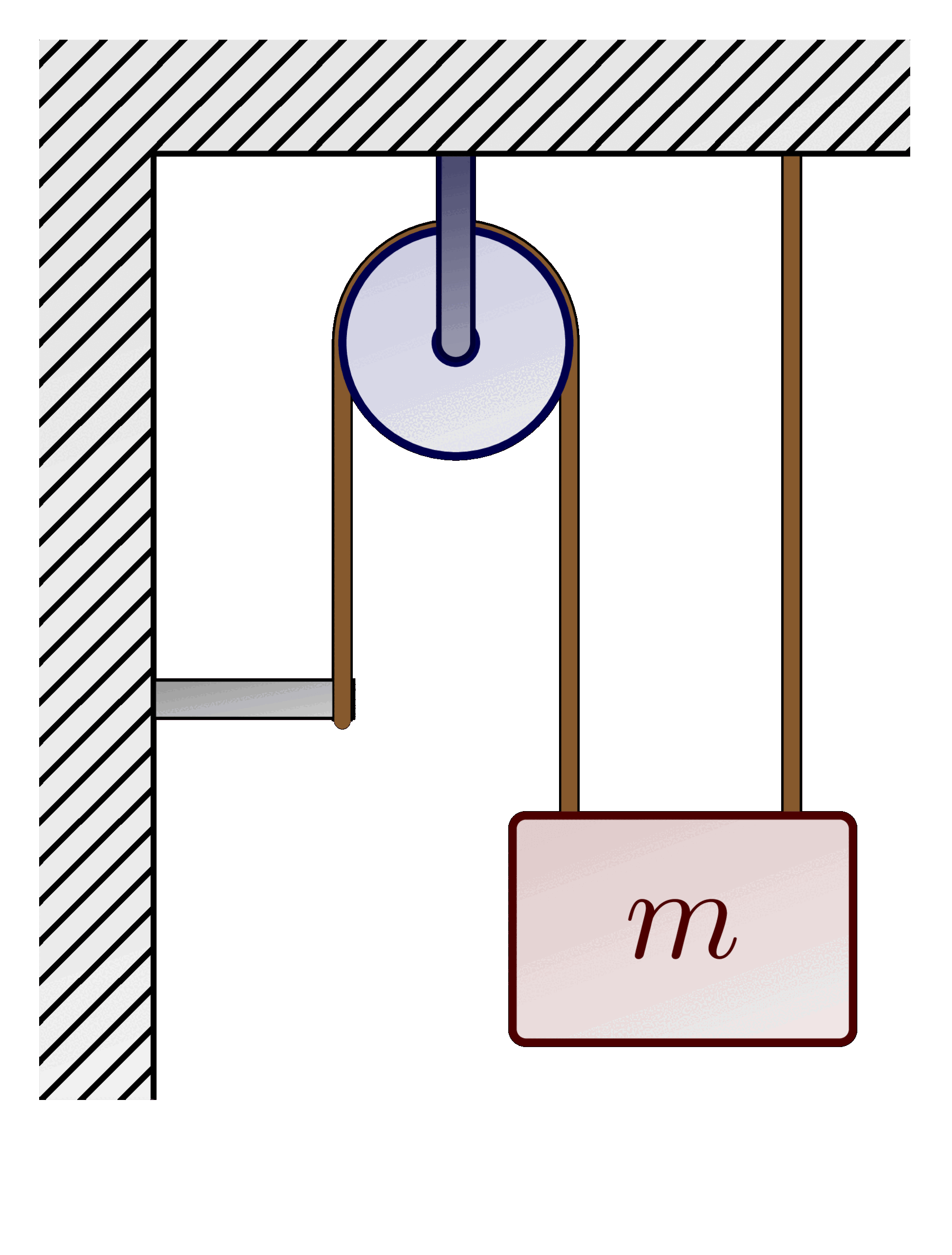
Dropping a mass in a gravitational field:

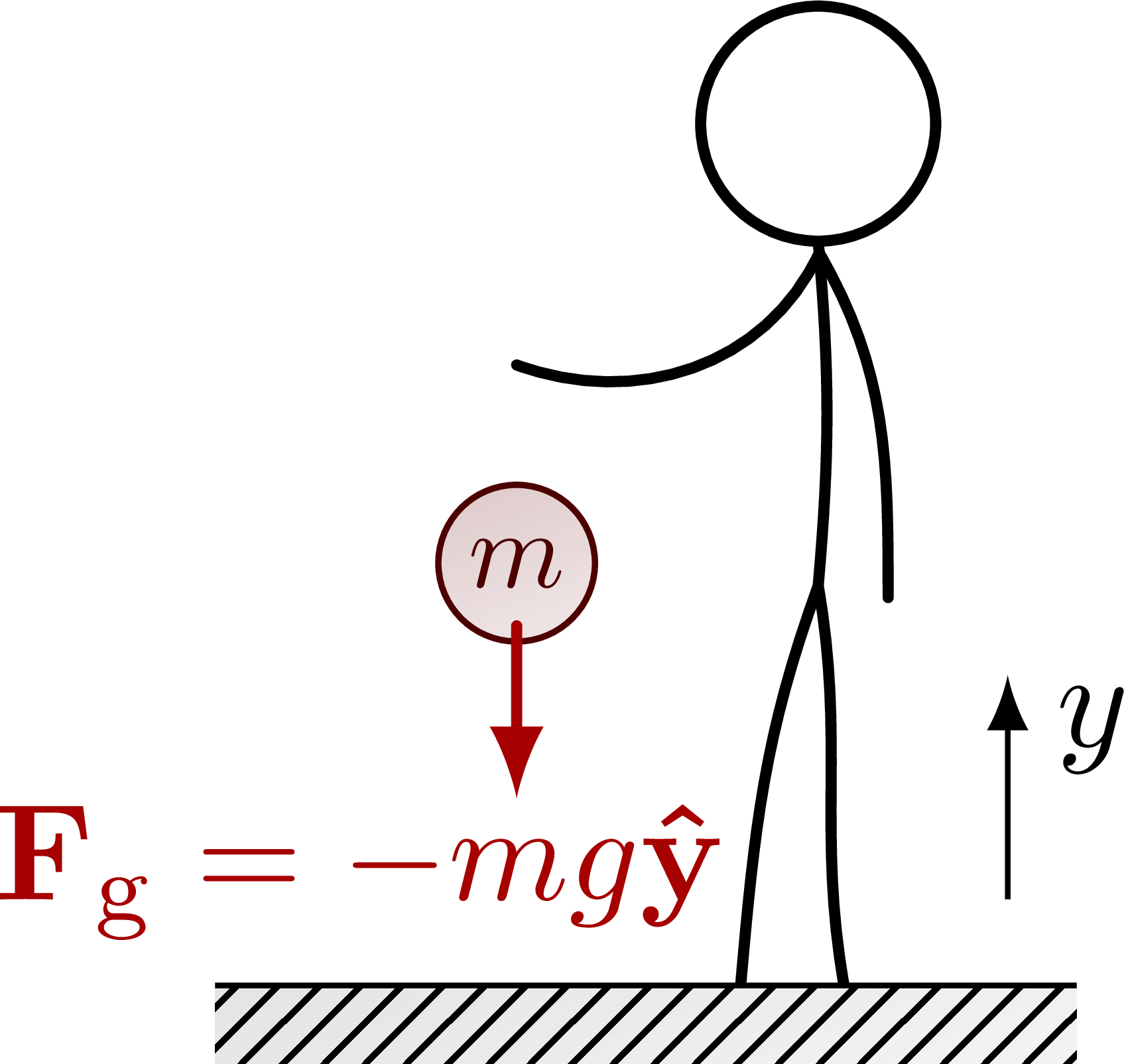
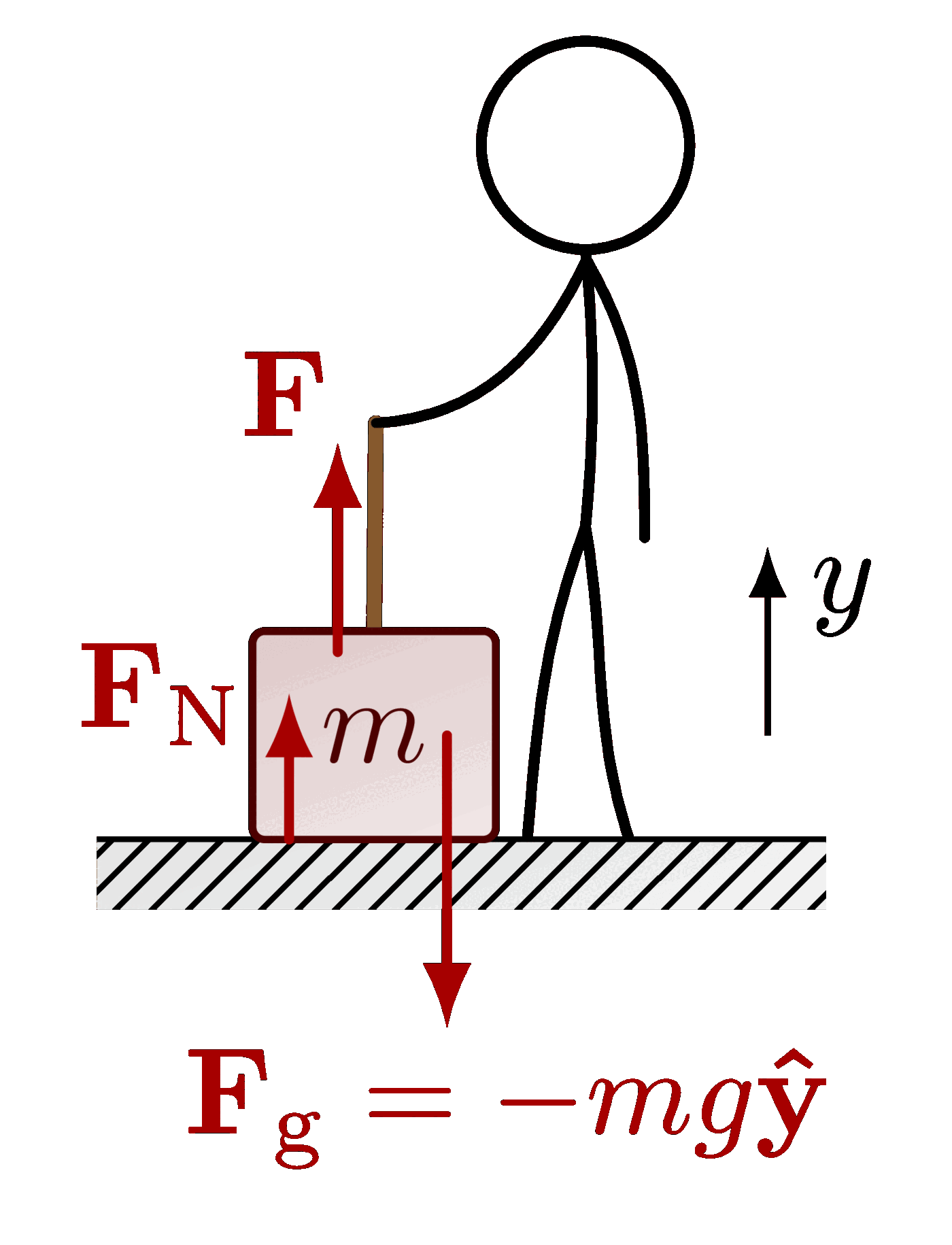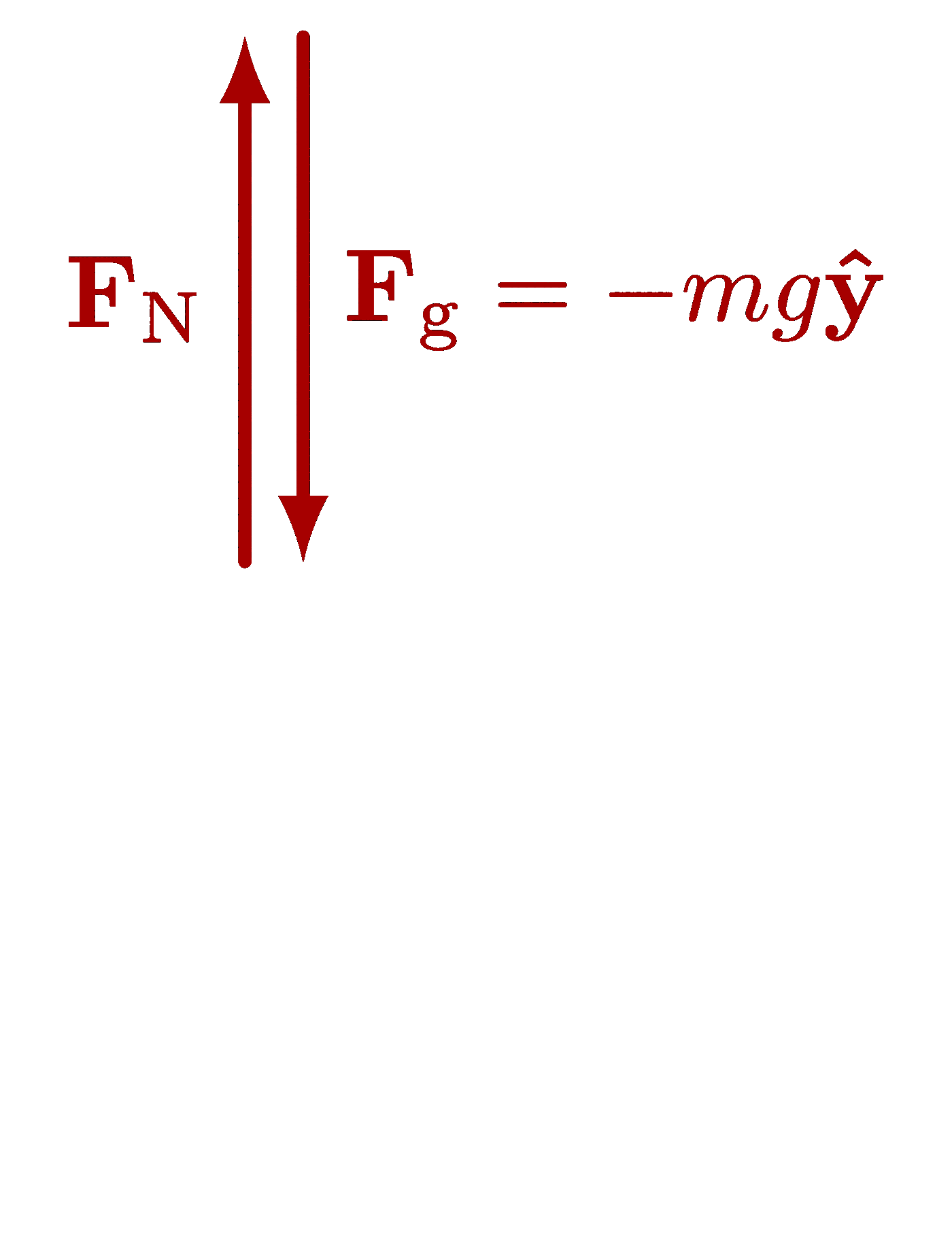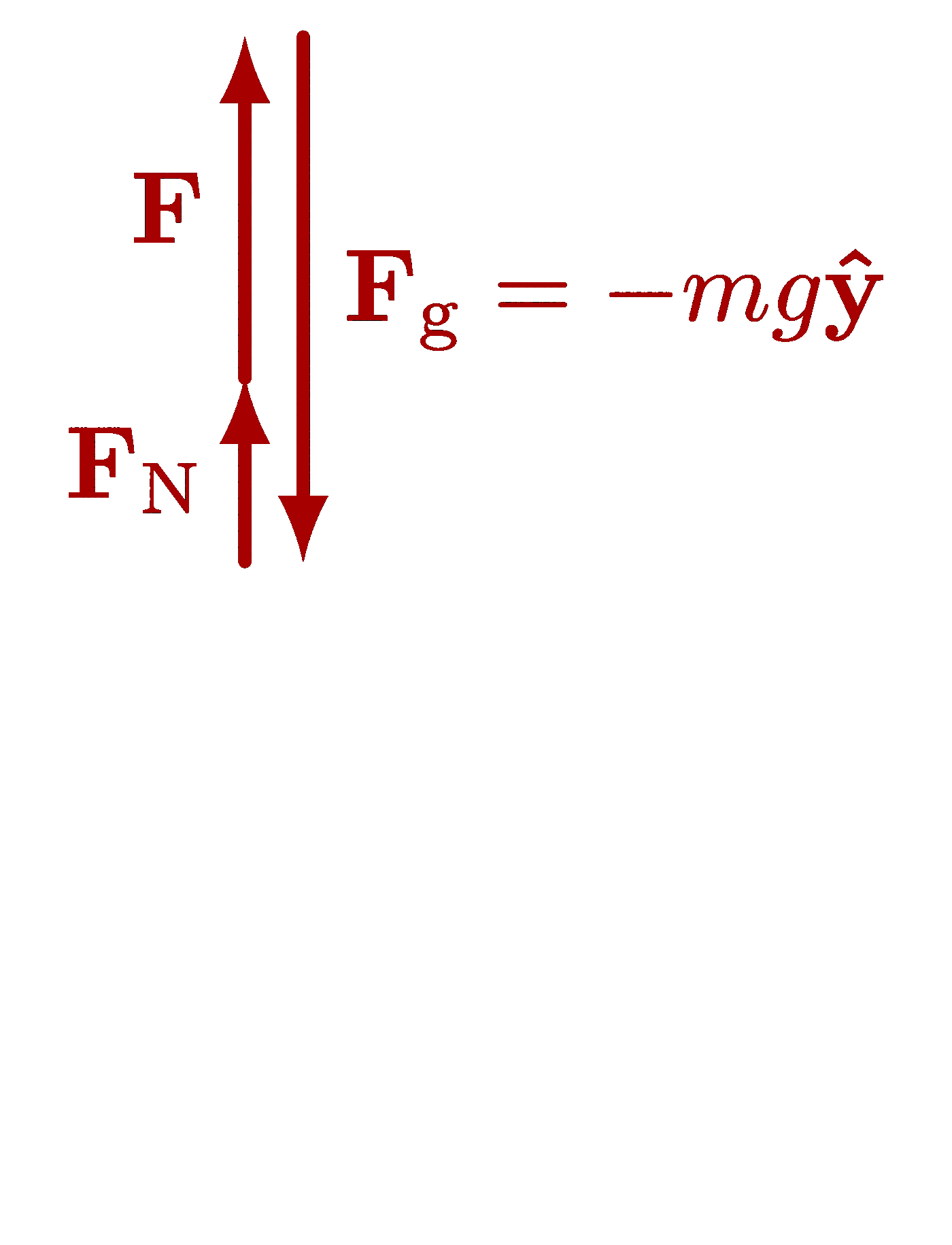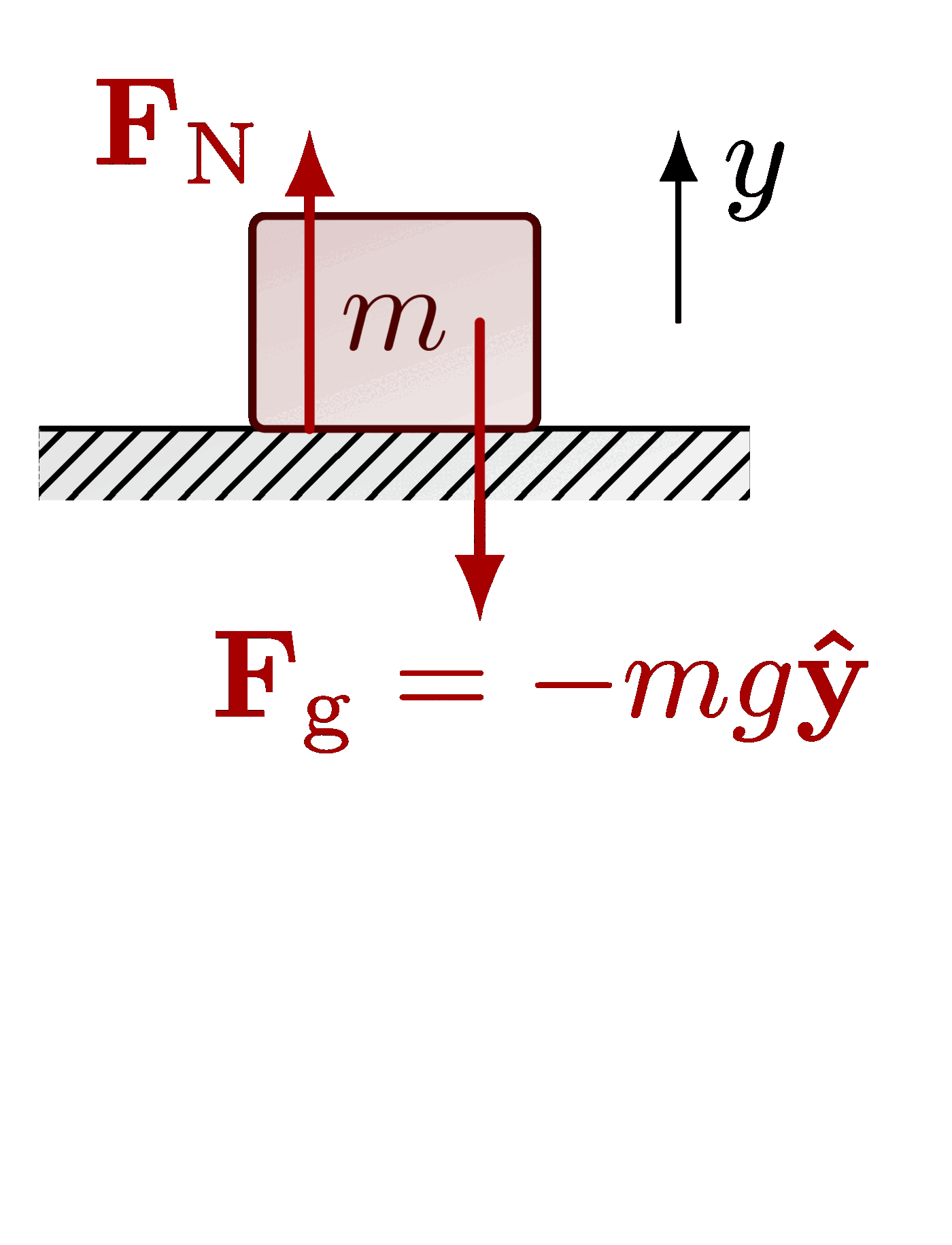
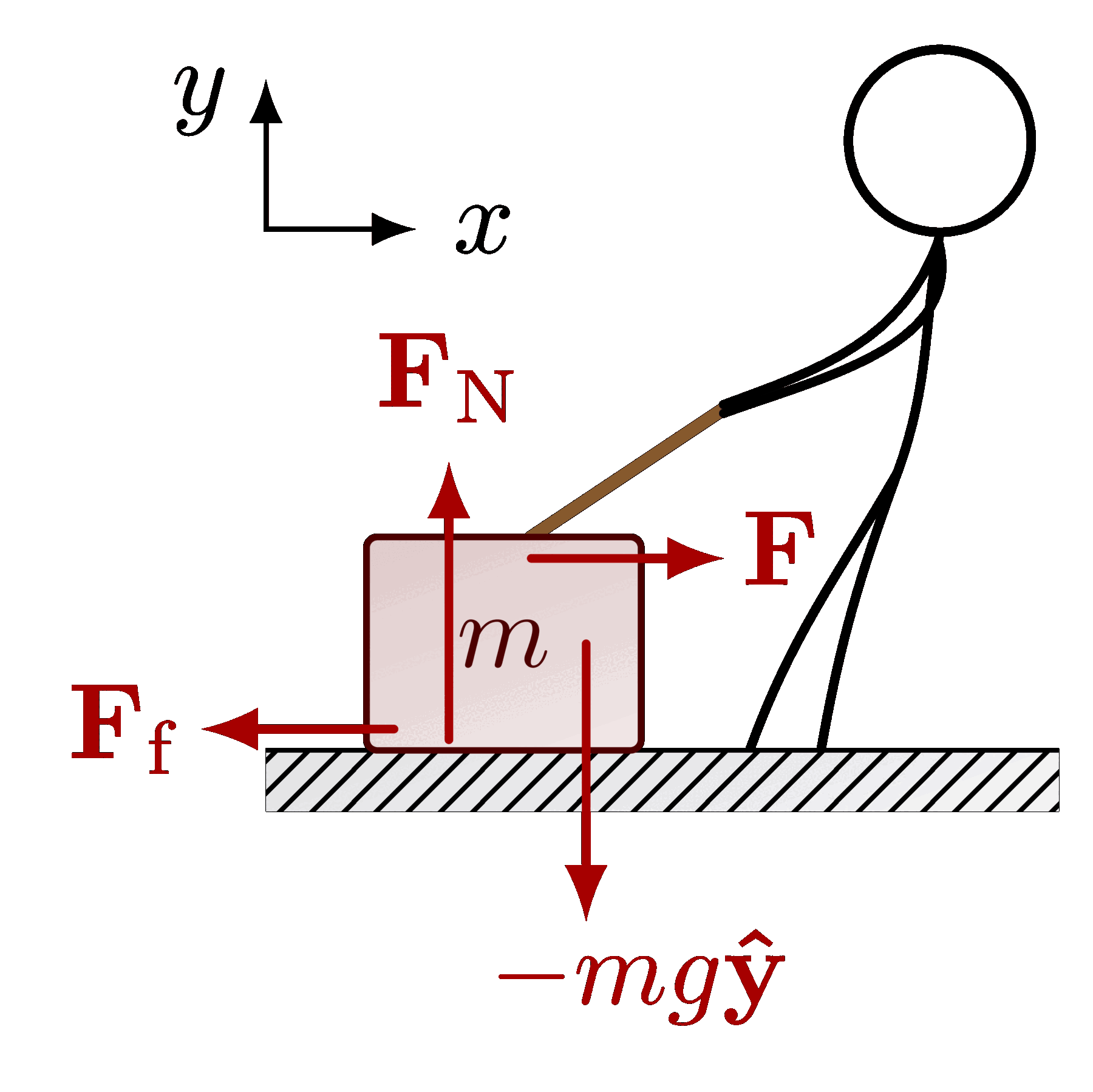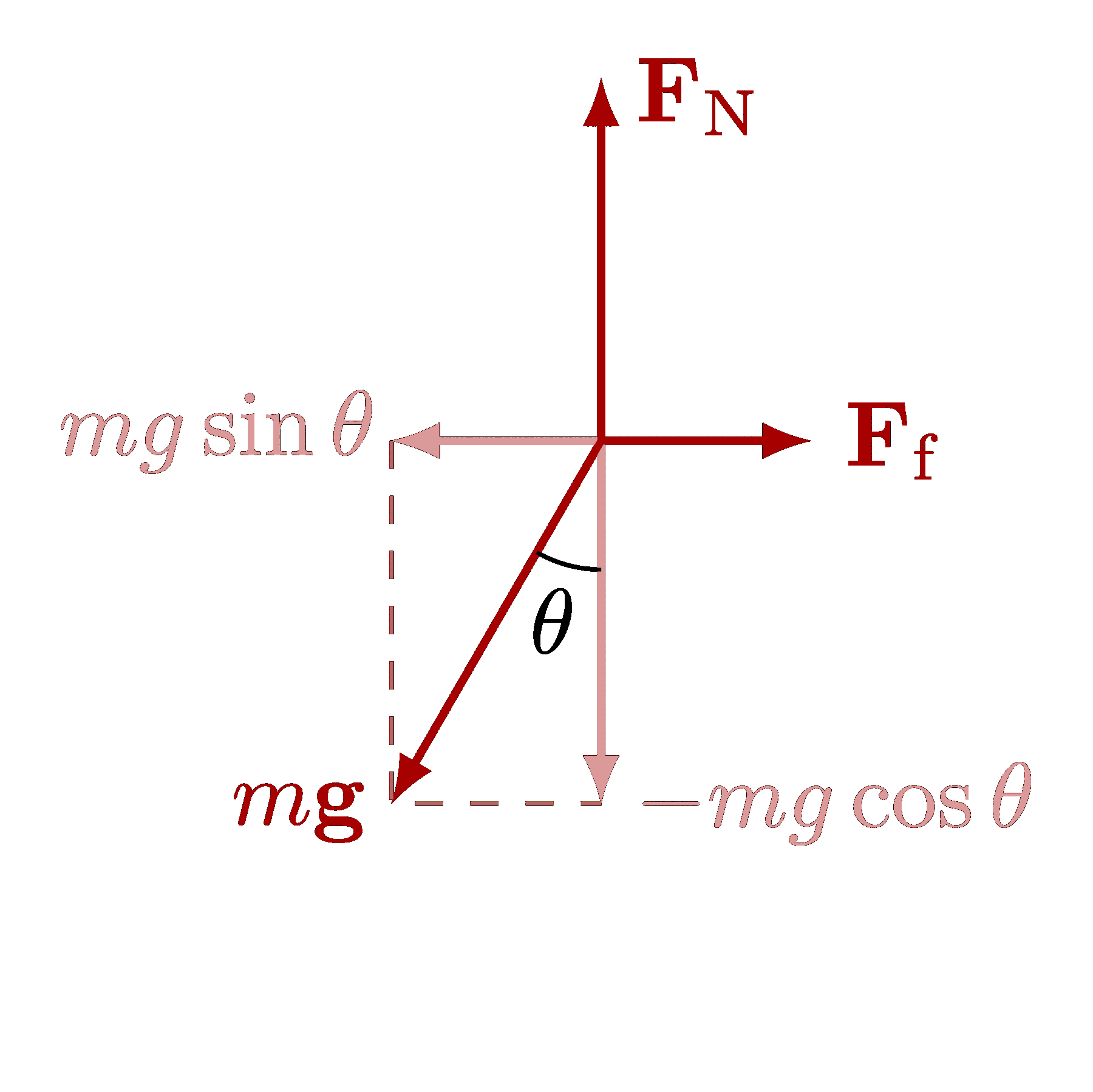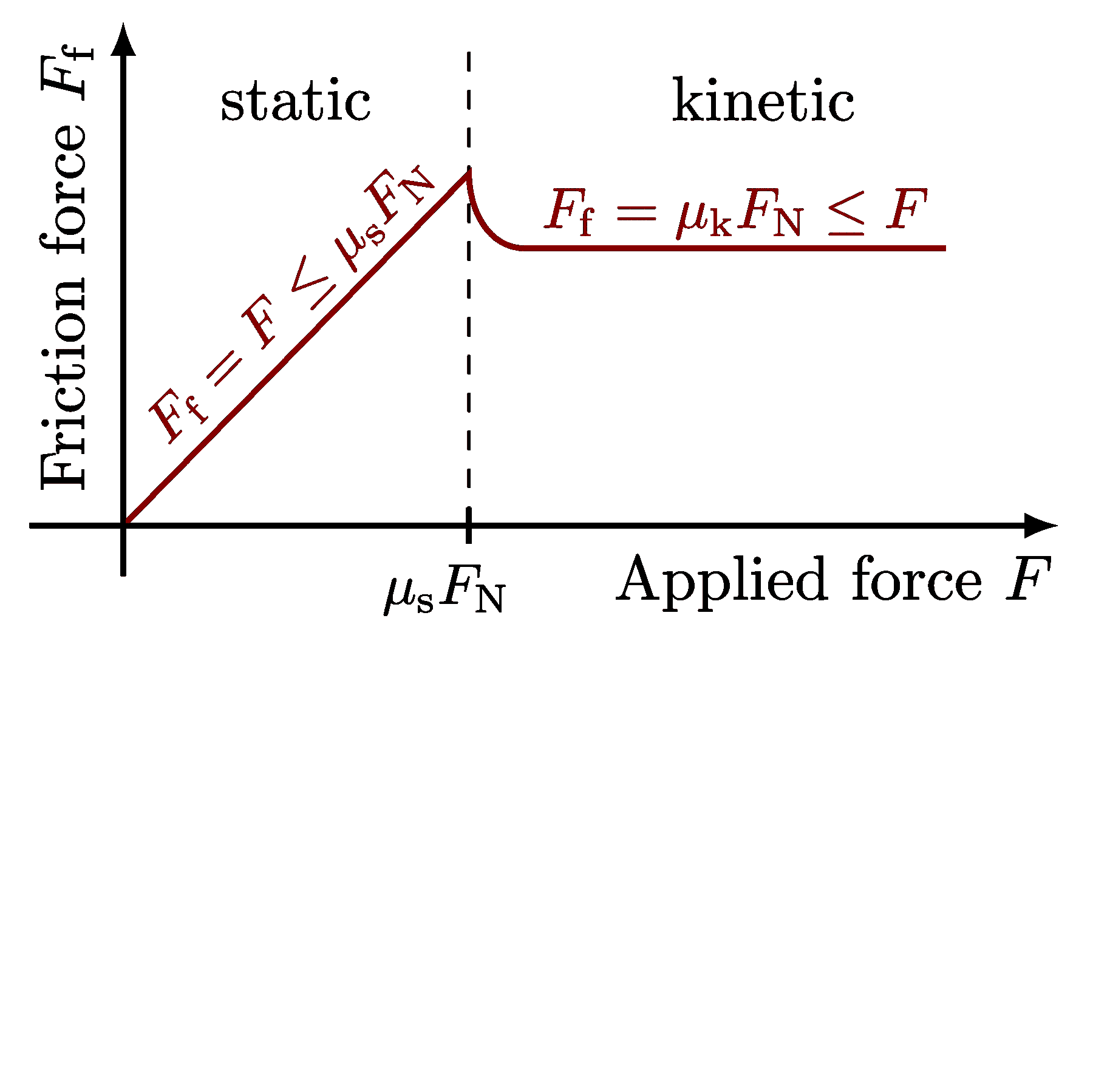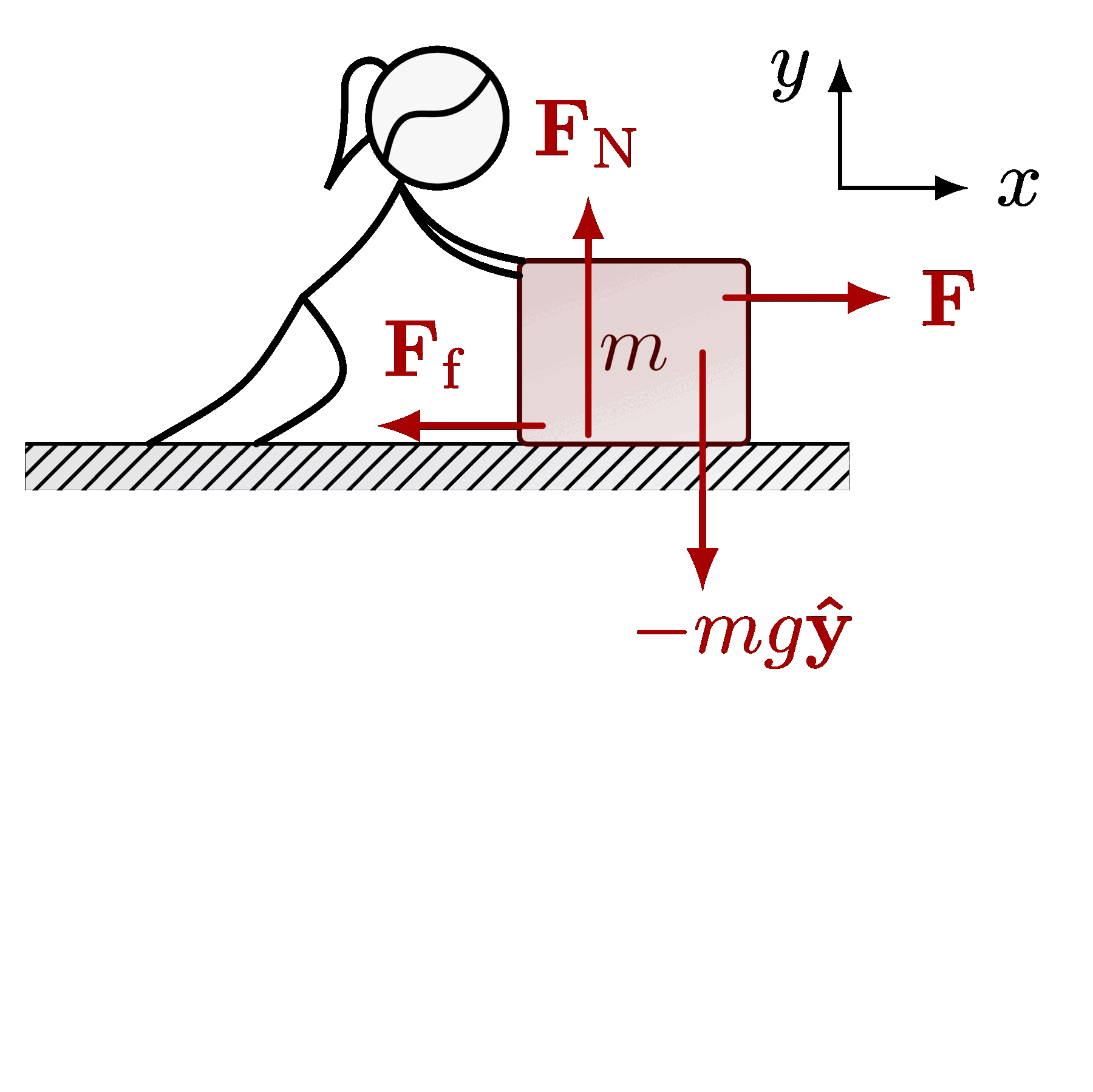
The gravitational field of a mass (also see normal forces):

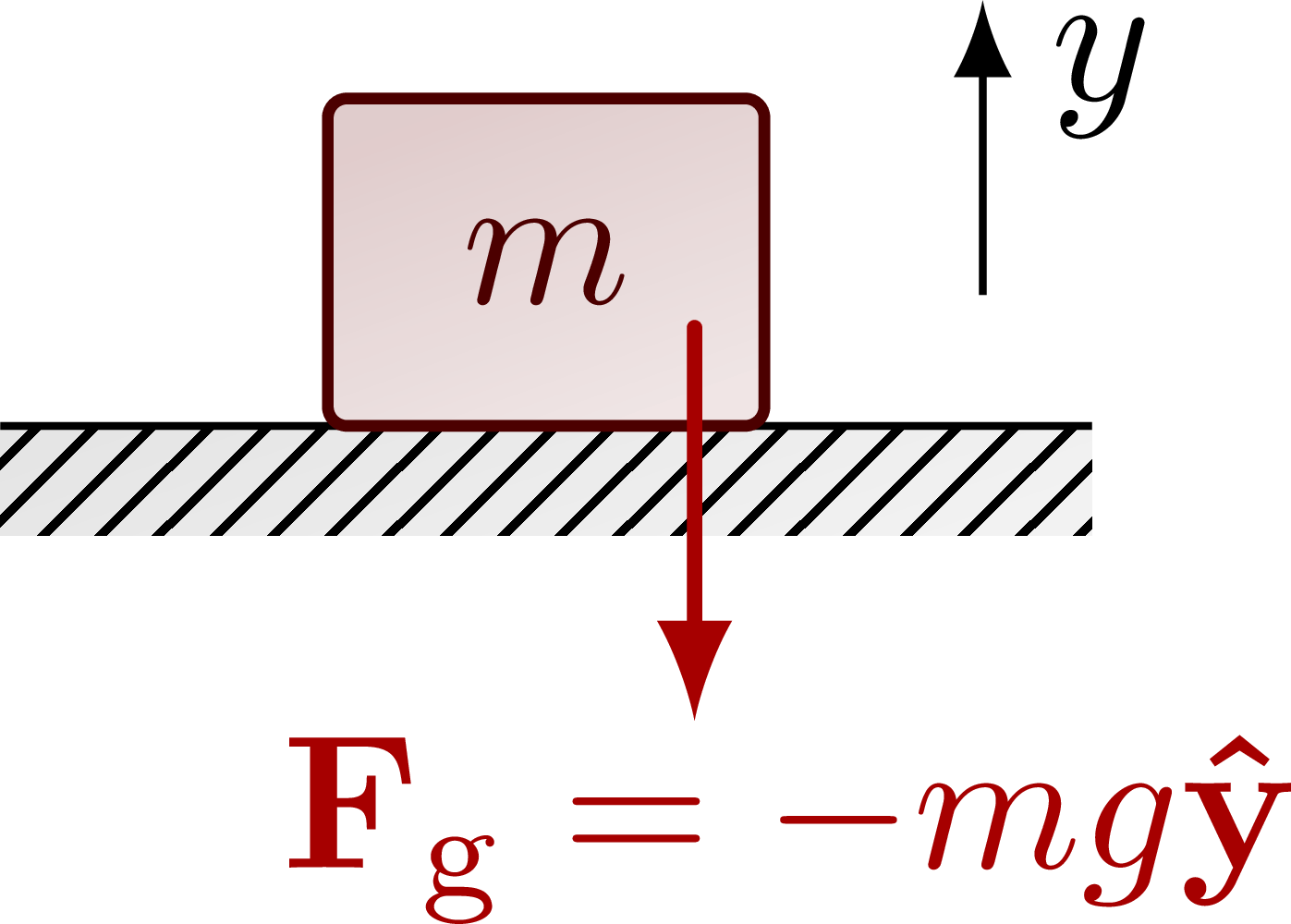
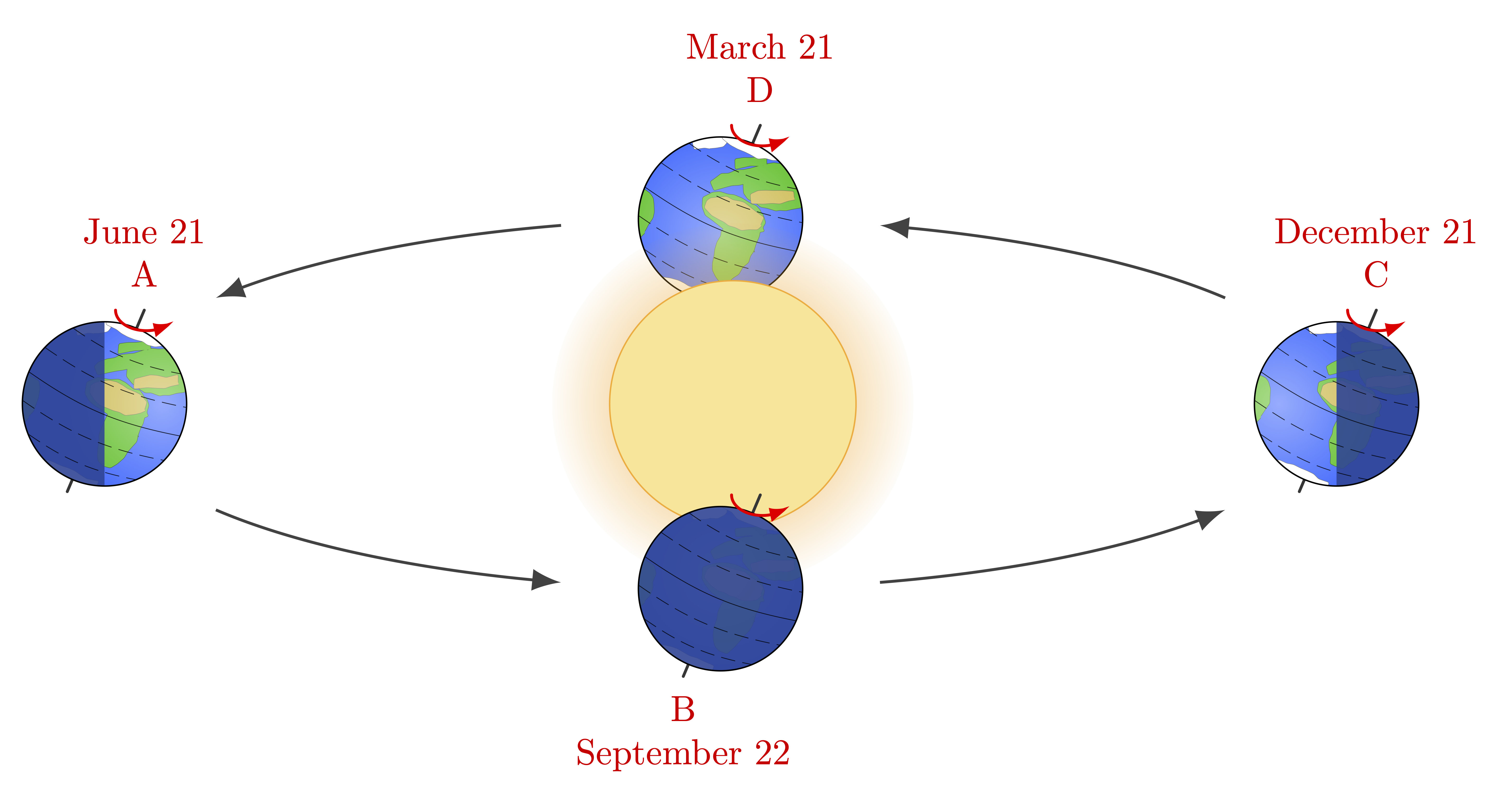
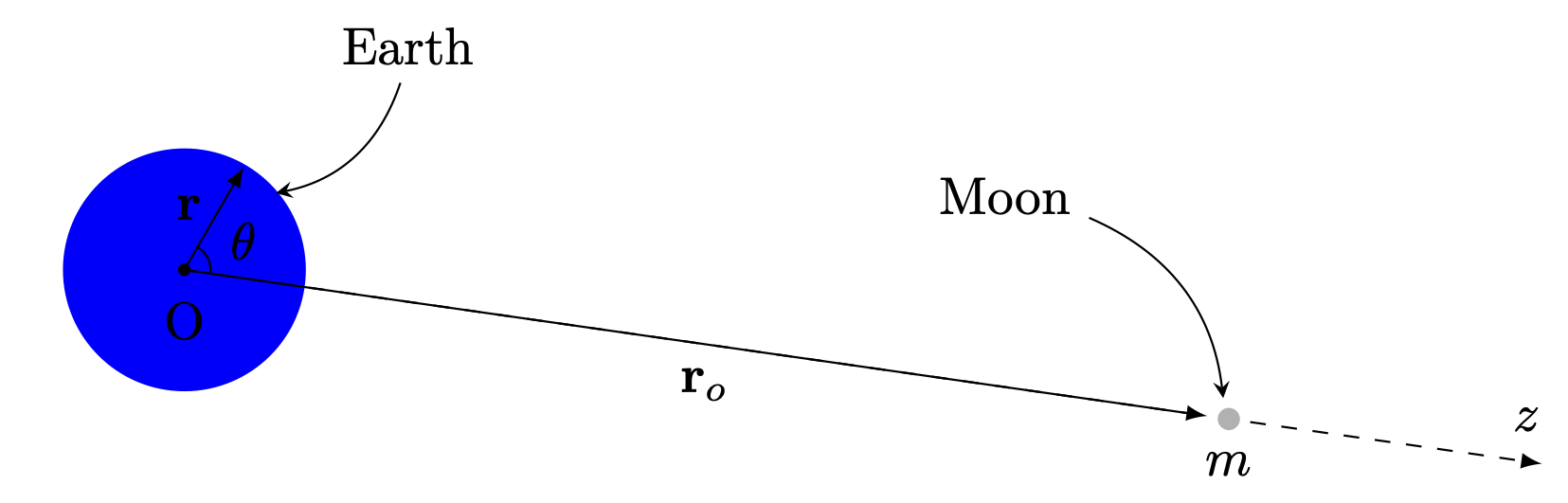
The gravitational field of the Earth:

The gravitational field close to the Earth’s surface:

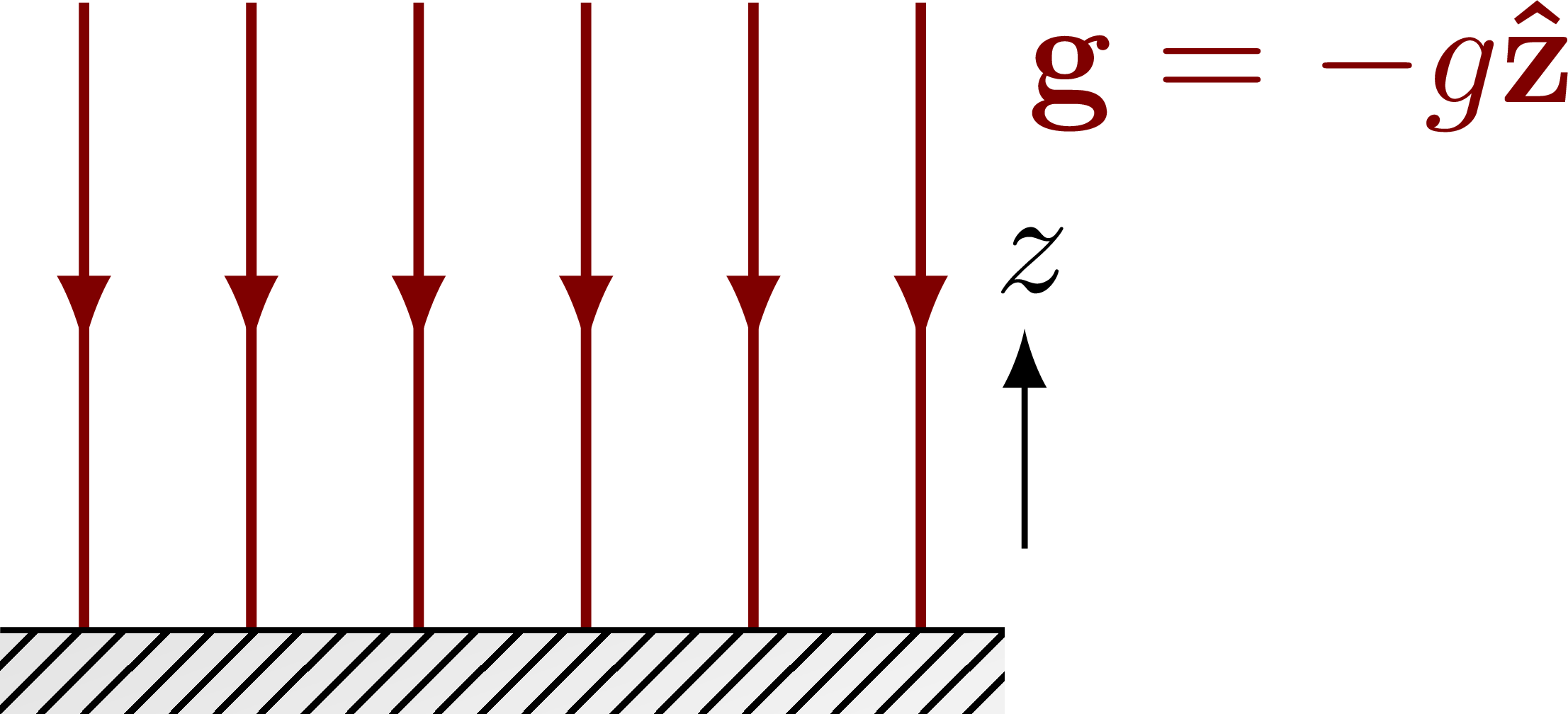
Edit and compile if you like:

% Author: Izaak Neutelings (Februari 2022)
\documentclass[border=3pt,tikz]{standalone}
\usepackage{physics}
\usepackage{tikz}
\usetikzlibrary{calc}
\usetikzlibrary{patterns}
\usetikzlibrary{arrows.meta} % for arrow size
\usetikzlibrary{decorations.markings}
\tikzset{>=latex} % for LaTeX arrow head

\colorlet{myred}{red!65!black}
\colorlet{mygreen}{green!60!black}
\colorlet{mydarkred}{red!50!black}
\colorlet{mydarkblue}{blue!40!black}
\tikzstyle{measure}=[{Latex[length=4,width=3]}-{Latex[length=4,width=3]},line width=0.4,mydarkblue]
\tikzstyle{ground}=[preaction={fill,top color=black!10,bottom color=black!5,shading angle=20},
                    fill,pattern=north east lines,draw=none,minimum width=0.3,minimum height=0.6]
\tikzstyle{mass}=[line width=0.6,red!30!black,fill=red!40!black!10,rounded corners=1,
                  top color=red!40!black!20,bottom color=red!40!black!10,shading angle=20]
\tikzstyle{rope}=[brown!70!black,line width=1.2,line cap=round] %very thick
\tikzstyle{force}=[->,myred,thick,line cap=round]
\tikzstyle{unit}=[->,mygreen,thick,line cap=round]
\tikzset{fieldlines/.style={mydarkred,decoration={markings,mark=at position #1 with {\arrow{latex}}},
                            postaction={decorate},line width=0.7},
         fieldlines/.default=0.55}
\newcommand{\vbF}{\vb{F}}


\begin{document}


% GRAVITATIONAL ATTRACTION
\begin{tikzpicture}
  \def\d{4.1}  % distance r
  \def\r{0.3}  % small radius ball
  \def\R{0.38} % large radius ball
  \def\F{0.95} % force magnitude
  \def\u{0.4}  % unit vector magnitude
  \def\ang{5}  % angle lin
  \coordinate (M1) at (0,0);
  \coordinate (M2) at (\ang:\d);
  
  % SETUP
  \draw[measure,-]
    (M1) --++ (\ang+90:1.6*\R)
    (M2) --++ (\ang+90:1.6*\R);
  \draw[measure] ($(M1)+(\ang+90:1.35*\R)$) --++ (M2)
    node[midway,circle,fill=white,inner sep=0] {$r$};
  \draw[dashed] (M1) -- (M2);
  \draw[mass] (M1) circle(\r) node[scale=0.9] {$m_1$};
  \draw[mass] (M2) circle(\R) node[scale=0.9] {$m_2$};
  
  % FORCES
  \draw[force] (M1)++(\ang-8:0.9*\r) --++ (\ang:\F)
    node[anchor=90,inner sep=4] {$\vbF_{21}$}; % = -G\dfrac{m_1m_2}{r^2}\vu{r}_{21}
  \draw[force] (M2)++(\ang-172:0.9*\R) --++ (\ang:-\F)
    node[anchor=130,inner sep=3] {$\vbF_{12}$}; % = -G\dfrac{m_1m_2}{r^2}\vu{r}_{12}
  \draw[unit] (M1)++(\ang+8:\r+0.02) --++ (\ang:\u)
    node[pos=0.8,above=-1] {$\vu{r}_{12}$};
  \draw[unit] (M2)++(\ang+172:\R+0.02) --++ (\ang:-\u)
    node[pos=0.6,above=-1] {$\vu{r}_{21}$};
  
\end{tikzpicture}


% DROPPING A MASS
\begin{tikzpicture}
  \def\W{2.2}  % ground width
  \def\D{0.2}  % ground depth
  \def\R{0.2}  % mass radius
  \def\H{2.2}  % human height
  \coordinate (RH) at (-0.15*\W,0.72*\H);
  \coordinate (M) at (-0.15*\W,0.49*\H);
  
  % SETUP
  \draw[ground] (-\W/2,0) rectangle++ (\W,-\D);
  \draw (-\W/2,0) --++ (\W,0);
  \draw[mass,line width=0.45] (M) circle(\R) node[scale=0.8] {$m$};
  
  % PERSON
  \draw[thick] (0.20*\W,\H) circle (0.3) coordinate (H); % head
  \draw[thick] (H)++(-90:0.3) coordinate (N) to[out=-85,in=85]++ (0,-0.40*\H) coordinate (P); % body
  \draw[thick,line cap=round] (N)++(-85:0.03) to[out=-115,in=-20] (RH); % right arm
  \draw[thick,line cap=round] (N)++(-85:0.03) to[out=-60,in=90]++ ( 0.08*\W,-0.4*\H); % left arm
  \draw[thick] (P) to[out=-110,in=85] (0.11*\W,0); % right leg
  \draw[thick] (P) to[out=-80,in=100] (0.23*\W,0); % left leg
  
  % FORCES
  \draw[->] (0.42*\W,0.10*\H) --++ (0,0.26*\H) node[below=4,right=0] {$y$};
  \draw[force] (M)++(0,-0.8*\R) --++ (0,-2.2*\R)
    node[anchor=25,inner sep=0] {$\vbF_\mathrm{g} = -mg\vu{y}$};
  
\end{tikzpicture}


% MASS ON A SURFACE
\begin{tikzpicture}
  \def\W{2.0} % ground width
  \def\D{0.2} % ground depth
  \def\h{0.6} % mass height
  \def\w{0.8} % mass width
  \draw[ground] (-\W/2,0) rectangle++ (\W,-\D);
  \draw (-\W/2,0) --++ (\W,0);
  \draw[mass] (-\w/2,0) rectangle++ (\w,\h) node[midway] {$m$};
  \draw[->] (1.0*\w,0.4*\h) --++ (0,0.9*\h) node[below=4,right=0] {$y$};
  \draw[force] (0.34*\w,0.3*\h) --++ (0,-1.2*\h)
    node[right=5,below=-3] {$\vbF_\mathrm{g} = -mg\vu{y}$};
\end{tikzpicture}


% GRAVITATIONAL FORCE FIELD of Earth
\begin{tikzpicture}
  \def\W{2.4}   % ground width
  \def\D{0.2}   % ground depth
  \def\H{1.5}   % height
  \def\E{0.35}  % Earth's radius
  \def\R{1.3}   % field line max. radius
  \def\N{10}    % number of field lines
  \def\rang{45} % angle or r axis
  
  % FIELD LINES
  \foreach \i [evaluate={\ang=\i*360/\N;}] in {1,...,\N}{
    \draw[fieldlines=0.6] (\ang:\R) -- (\ang:\E); % field lines
  }
  \node[mydarkred,right] at (30:0.71*\R) {$\vb{g} = -\dfrac{gm}{r^2}\vu{r}$};
  \draw[->] (\rang:0.44*\R) --++ (\rang:0.4*\R) node[anchor=\rang+170,inner sep=1] {$r$};
  
  % EARTH
  \fill[blue!70!black!70] (0,0) circle(\E);
  \begin{scope}[rotate=-11]
    \clip (0,0) circle(\E);
    \fill[white] (0,\E) ellipse({0.6*\E} and {0.15*\E});
    \fill[white] (0,-\E) ellipse({0.8*\E} and {0.08*\E});
    \fill[green!70!black!60,rotate=-30] (160:1.1*\E) ellipse({0.2*\E} and {0.8*\E});
    \fill[green!70!black!60,rotate=40] (-10:1.14*\E) ellipse({0.2*\E} and {0.9*\E});
    \fill[green!60!black!60,very thick,rotate=-20] % Australia
      (230:0.86*\E) ellipse({0.25*\E} and {0.18*\E});
  \end{scope}
  \draw[line width=0.3] (0,0) circle(\E);
  
\end{tikzpicture}


% GRAVITATIONAL FORCE FIELD on Earth's surface
\begin{tikzpicture}
  \def\W{2.4} % ground width
  \def\D{0.2} % ground depth
  \def\H{1.5} % height
  \def\N{6}   % number of field lines
  \draw[->] (1.02*\W,0.13*\H) --++ (0,0.35*\H) node[right=0.5,above=-1] {$z$};
  \node[mydarkred,right=-2] at (\W,0.9*\H) {$\vb{g} = -g\vu{z}$};
  \foreach \i [evaluate={\x=(\i-0.5)*\W/\N;}] in {1,...,\N}{
    \draw[fieldlines] (\x,\H) -- (\x,0); % field lines
  }
  \draw[ground] (0,0) rectangle++ (\W,-\D);
  \draw (0,0) -- (\W,0);
\end{tikzpicture}


\end{document}

Click to download: dynamics_gravity.tex • dynamics_gravity.pdf
Open in Overleaf: dynamics_gravity.tex.