Random circles

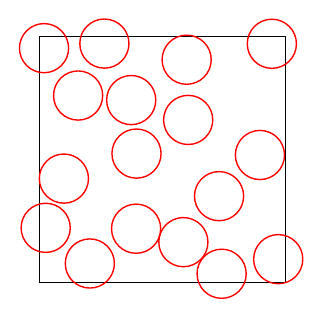
Here’s a macro that fills a part of a picture with more or less evenly and randomly distributed circles that don’t overlap. It takes four arguments: The width and height of the rectangle to be filled, the radius of the circles, and the number of attempts.

For each attempt, a random position is generated. The distances between this position and all existing circles are calculated, and if there’s a collision, no circle is drawn. If the circle does not collide, it is drawn, and its coordinates are added to the list of existing circles.

This approach is far from efficient, but it works.

\documentclass[tikz,border=10pt]{standalone}
\begin{document}
\def\xlist{4}
\def\ylist{4}

\newcommand{\fillrandomly}[4]{
    \pgfmathsetmacro\diameter{#3*2}
    \draw (0,0) rectangle (#1,#2);
    \foreach \i in {1,...,#4}{
        \pgfmathsetmacro\x{rnd*#1}
        \pgfmathsetmacro\y{rnd*#2}
        \xdef\collision{0}
        \foreach \element [count=\i] in \xlist{
            \pgfmathtruncatemacro\j{\i-1}
            \pgfmathsetmacro\checkdistance{ sqrt( ({\xlist}[\j]-(\x))^2 + ({\ylist}[\j]-(\y))^2 ) }
            \ifdim\checkdistance pt<\diameter pt
                \xdef\collision{1}
                \breakforeach
            \fi
        }
        \ifnum\collision=0
            \xdef\xlist{\xlist,\x}
            \xdef\ylist{\ylist,\y}
            \draw [red, thick] (\x,\y) circle [radius=#3];
        \fi 

    }
}

\begin{tikzpicture}
\pgfmathsetseed{2}
\fillrandomly{5}{5}{0.5}{300}

\end{tikzpicture}
\end{document}