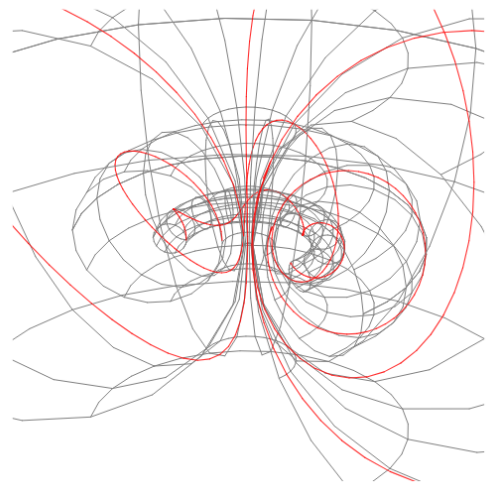
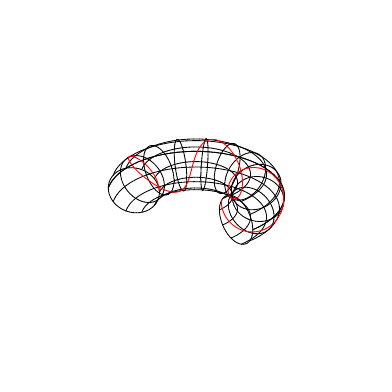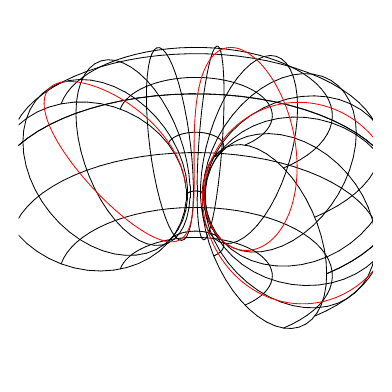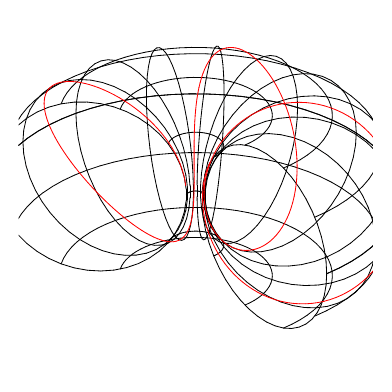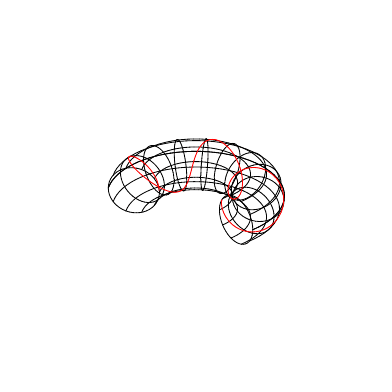
I thought it would be cool to show how to make stereographically nested toroidal solenoids.
Essentially, we make stereographically nested tori, and then we find their solenoid.
In the code below there are functions which determine the two radii of the torus; namely, “radius” and “centershift”.
Try setting different values for \toggleangle, and \frequency!
Modifying the \toggleangle will produce the transformation shown in the .gif, and \frequency will change the frequency of the solenoids.
\documentclass[tikz, border=3.14mm]{standalone}
\usepackage{tikz-3dplot}
\pgfmathdeclarefunction{sphereX}{2}{%
% #1 - longitude
% #2 - latitude
\pgfmathparse{cos(#2)*cos(#1)}%
}
\pgfmathdeclarefunction{sphereY}{2}{%
% #1 - longitude
% #2 - latitude
\pgfmathparse{cos(#2)*sin(#1)}%
}
\pgfmathdeclarefunction{sphereZ}{2}{%
% #1 - longitude
% #2 - latitude
\pgfmathparse{sin(#2)}%
}
\pgfmathdeclarefunction{radius}{1}{%
\pgfmathparse{
sqrt(
1 / cos(#1)^2 -
cos(#1)
)
}%
}
\pgfmathdeclarefunction{centershift}{1}{%
\pgfmathparse{1 / cos(#1)}%
}
\begin{document}
\tdplotsetmaincoords{60}{80}
\begin{tikzpicture}[tdplot_main_coords]
\clip[tdplot_screen_coords] (-3,-3) rectangle (3,3);
\foreach \toggleangle in {%
10%
,40%
,70%
}{
% lines of longitude
\pgfmathsetmacro{\startlatitude}{0}
\pgfmathsetmacro{\endlatitude}{360}
\pgfmathsetmacro{\sampleslatitude}{10}
\pgfmathsetmacro{\steplatitude}{
(\endlatitude-\startlatitude) /
\sampleslatitude
}
\foreach \latitude[parse = true] in {%
\startlatitude%
,\startlatitude+\steplatitude%
,...%
,\endlatitude%
}{
\pgfmathsetmacro{\startlongitude}{30}
\pgfmathsetmacro{\endlongitude}{250}
\pgfmathsetmacro{\sampleslongitude}{20}
\pgfmathsetmacro{\steplongitude}{
(\endlongitude - \startlongitude) /
\sampleslongitude
}
\foreach \longitude[
parse = true
,count = \count
] in {%
\startlongitude%
,\startlongitude+\steplongitude%
,...%
,\endlongitude%
} {
\pgfmathparse{\count != \sampleslongitude + 1}
\ifnum\pgfmathresult=1
\draw[line cap = round,ultra thin,gray] (
{
sphereX(\longitude,\latitude) *
radius(\toggleangle) +
centershift(\toggleangle) *
cos(\longitude)
}
,{
sphereY(\longitude,\latitude) *
radius(\toggleangle) +
centershift(\toggleangle) *
sin(\longitude)
}
,{
sphereZ(\longitude,\latitude) *
radius(\toggleangle)
}
) -- (
{
sphereX(\longitude+\steplongitude,\latitude) *
radius(\toggleangle) +
centershift(\toggleangle) *
cos(\longitude+\steplongitude)
}
,{
sphereY(\longitude+\steplongitude,\latitude) *
radius(\toggleangle) +
centershift(\toggleangle) *
sin(\longitude+\steplongitude)
}
,{
sphereZ(\longitude+\steplongitude,\latitude) *
radius(\toggleangle)
}
);
\fi
}
}
% lines of latitude
\pgfmathsetmacro{\startlongitude}{30}
\pgfmathsetmacro{\endlongitude}{250}
\pgfmathsetmacro{\sampleslongitude}{10}
\pgfmathsetmacro{\steplongitude}{
(\endlongitude - \startlongitude) /
\sampleslongitude
}
\foreach \longitude[parse = true] in {%
\startlongitude%
,\startlongitude+\steplongitude%
,...%
,\endlongitude%
} {
\pgfmathsetmacro{\startlatitude}{0}
\pgfmathsetmacro{\endlatitude}{360}
\pgfmathsetmacro{\sampleslatitude}{20}
\pgfmathsetmacro{\steplatitude}{
(\endlatitude-\startlatitude) /
\sampleslatitude
}
\foreach \latitude[
parse = true
,count = \count
] in {%
\startlatitude%
,\startlatitude+\steplatitude%
,...%
,\endlatitude%
} {
\pgfmathparse{\count != \sampleslatitude + 1}
\ifnum\pgfmathresult=1
\draw[line cap = round,ultra thin,gray] (
{
sphereX(\longitude,\latitude) *
radius(\toggleangle) +
centershift(\toggleangle) *
cos(\longitude)
}
,{
sphereY(\longitude,\latitude) *
radius(\toggleangle) +
centershift(\toggleangle) *
sin(\longitude)
}
,{
sphereZ(\longitude,\latitude) *
radius(\toggleangle)
}
) -- (
{
sphereX(\longitude,\latitude+\steplatitude) *
radius(\toggleangle) +
centershift(\toggleangle) *
cos(\longitude)
}
,{
sphereY(\longitude,\latitude+\steplatitude) *
radius(\toggleangle) +
centershift(\toggleangle) *
sin(\longitude)
}
,{
sphereZ(\longitude,\latitude+\steplatitude) *
radius(\toggleangle)
}
);
\fi
}
}
% toroidal solenoids
\pgfmathsetmacro{\frequency}{5}
\pgfmathsetmacro{\sampleslongitude}{150}
\pgfmathsetmacro{\steplongitude}{
(\endlongitude - \startlongitude) /
\sampleslongitude
}
\foreach \longitude [parse = true] in {%
\startlongitude%
,\startlongitude+\steplongitude%
,...%
,\endlongitude%
} {
\draw[red,line cap = round,opacity=0.8] (
{
(
centershift(\toggleangle) +
radius(\toggleangle) *
cos(\frequency*\longitude)
) * cos(\longitude)
}
,{
(
centershift(\toggleangle) +
radius(\toggleangle) *
cos(\frequency*\longitude)
) * sin(\longitude)
}
,{
radius(\toggleangle) *
sin(\frequency*\longitude)
}
) -- (
{
(
centershift(\toggleangle) +
radius(\toggleangle) *
cos(\frequency*(\longitude+\steplongitude))
) * cos(\longitude+\steplongitude)
}
,{
(
centershift(\toggleangle) +
radius(\toggleangle) *
cos(\frequency*(\longitude+\steplongitude))
) * sin(\longitude+\steplongitude)
}
,{
radius(\toggleangle) *
sin(\frequency*(\longitude+\steplongitude))
}
);
}
}
\end{tikzpicture}
\end{document}


