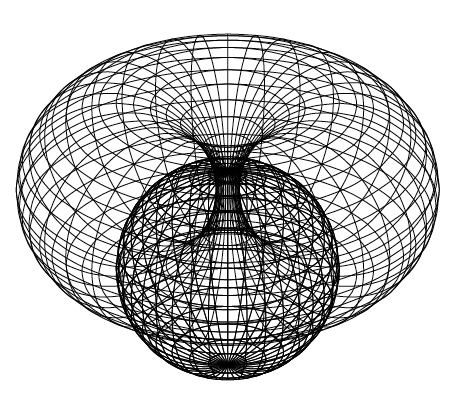
This is an interesting stereographic projection that you get when you rotate 90-degree Steiner circles about their axis of symmetry.
Animated GIF; you may need to click on it for running:
This is an example LaTeX file for a particular value of \animationparameter, that you can run yourself here in the browser:
\documentclass[
tikz
,border = 3.14mm
]{standalone}
\usepackage{tikz-3dplot}
\pgfmathdeclarefunction{sphereX}{2}{%
% #1 - longitude
% #2 - latitude
\pgfmathparse{cos(#2)*cos(#1)}%
}
\pgfmathdeclarefunction{sphereY}{2}{%
\pgfmathparse{cos(#2)*sin(#1)}%
}
\pgfmathdeclarefunction{sphereZ}{2}{%
\pgfmathparse{sin(#2)}%
}
\pgfmathdeclarefunction{toruscenter}{1}{%
% #1 - \animationparameter
\pgfmathparse{1/cos(#1)}%
}
\pgfmathdeclarefunction{torusradius}{1}{%
% #1 - \animationparameter
\pgfmathparse{-sin(#1)/cos(#1)}%
}
\pgfmathdeclarefunction{projectionx}{3}{%
% #1 - \animationparameter
% #2 - \longitude
% #2 - \latitude
\pgfmathparse{
torusradius(#1) *
sphereX(#2,#3) +
toruscenter(#1) *
cos(#2)
}%
}
\pgfmathdeclarefunction{projectiony}{3}{%
% #1 - \animationparameter
% #2 - \longitude
% #2 - \latitude
\pgfmathparse{
torusradius(#1) *
sphereY(#2,#3) +
toruscenter(#1) *
sin(#2)
}%
}
\pgfmathdeclarefunction{projectionz}{3}{%
% #1 - \animationparameter
% #2 - \longitude
% #2 - \latitude
\pgfmathparse{
torusradius(#1) *
sphereZ(#2,#3)
}%
}
\pgfmathsetmacro{\animationparameter}{60}
\begin{document}
\tdplotsetmaincoords{60}{120}
\begin{tikzpicture}[tdplot_main_coords]
% This clips and adds struts to a rectangle
% which mimicks the size of a Beamer frame.
\path[tdplot_screen_coords]
(-12.8/2,-9.6/2)
rectangle
(12.8/2,9.6/2);
\clip[tdplot_screen_coords]
(-12.8/2,-9.6/2)
rectangle
(12.8/2,9.6/2);
\pgfmathsetmacro{\startlatitude}{0}
\pgfmathsetmacro{\endlatitude}{360}
\pgfmathsetmacro{\sampleslatitude}{20}
\pgfmathsetmacro{\steplatitude}{
(\endlatitude - \startlatitude) /
\sampleslatitude
}
\foreach
\latitude[
parse = true
,count = \count
]
in {%
\startlatitude%
,\startlatitude+\steplatitude%
,...%
,\endlatitude%
} {
\pgfmathparse{\count != \sampleslatitude + 1}
\ifnum\pgfmathresult=1
\pgfmathsetmacro{\startlongitude}{0}
\pgfmathsetmacro{\endlongitude}{360}
\pgfmathsetmacro{\sampleslongitude}{20}
\draw[
smooth
,domain = \startlongitude:\endlongitude
,samples = \sampleslongitude
,variable = \longitude
] plot (
{
projectionx(
\animationparameter
,\longitude
,\latitude
)
}
,{
projectiony(
\animationparameter
,\longitude
,\latitude
)
}
,{
projectionz(
\animationparameter
,\longitude
,\latitude
)
}
) plot (
{
toruscenter(\animationparameter) *
sphereX(\longitude,\latitude)
}
,{
toruscenter(\animationparameter) *
sphereY(\longitude,\latitude)
}
,{
toruscenter(\animationparameter) *
sphereZ(\longitude,\latitude) +
torusradius(\animationparameter)
}
);
\fi
}
\pgfmathsetmacro{\startlongitude}{0}
\pgfmathsetmacro{\endlongitude}{360}
\pgfmathsetmacro{\sampleslongitude}{20}
\pgfmathsetmacro{\steplongitude}{
(\endlongitude - \startlongitude) /
\sampleslongitude
}
\foreach
\longitude[
parse = true
,count = \count
]
in {%
\startlongitude%
,\startlongitude+\steplongitude%
,...%
,\endlongitude%
} {
\pgfmathparse{\count != \sampleslongitude + 1}
\ifnum\pgfmathresult=1
\pgfmathsetmacro{\startlatitude}{0}
\pgfmathsetmacro{\endlatitude}{360}
\pgfmathsetmacro{\sampleslatitude}{20}
\draw[
smooth
,domain = \startlatitude:\endlatitude
,samples = \sampleslatitude
,variable = \latitude
] plot (
{
projectionx(
\animationparameter
,\longitude
,\latitude
)
}
,{
projectiony(
\animationparameter
,\longitude
,\latitude
)
}
,{
projectionz(
\animationparameter
,\longitude
,\latitude
)
}
) plot (
{
toruscenter(\animationparameter) *
sphereX(\longitude,\latitude)
}
,{
toruscenter(\animationparameter) *
sphereY(\longitude,\latitude)
}
,{
toruscenter(\animationparameter) *
sphereZ(\longitude,\latitude) +
torusradius(\animationparameter)
}
);
\fi
}
\end{tikzpicture}
\end{document}