FIR with Adder Tree
FIR of 8 taps (number of h_i coefficients) with Adder Tree:
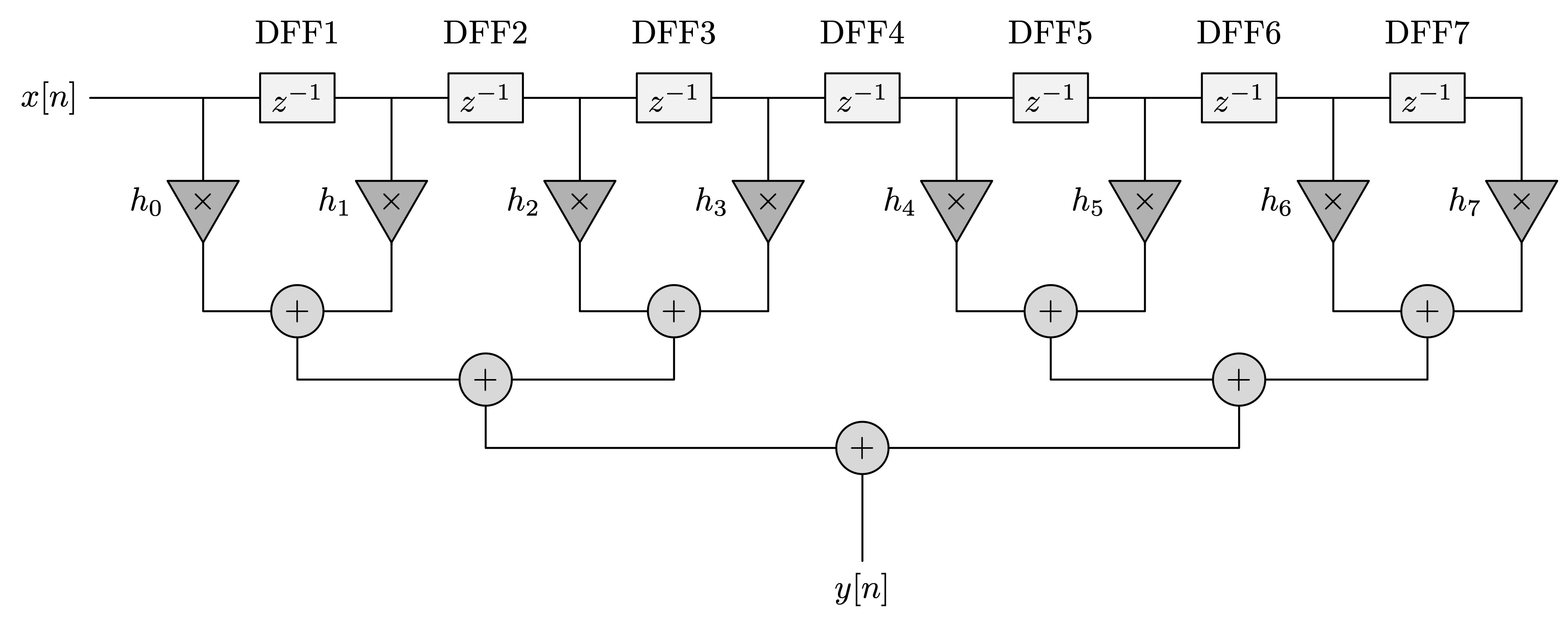
Waveforms
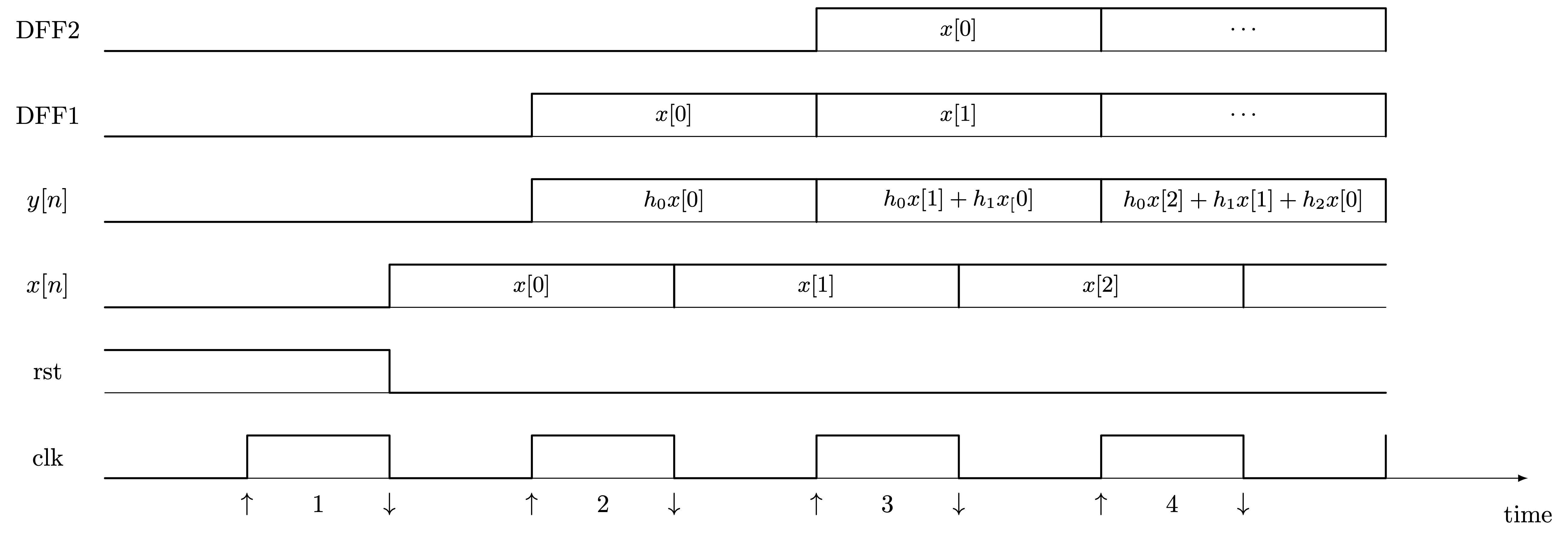
Pipelined FIR with Adder Tree
Pipelined FIR of 8 taps with Adder Tree:
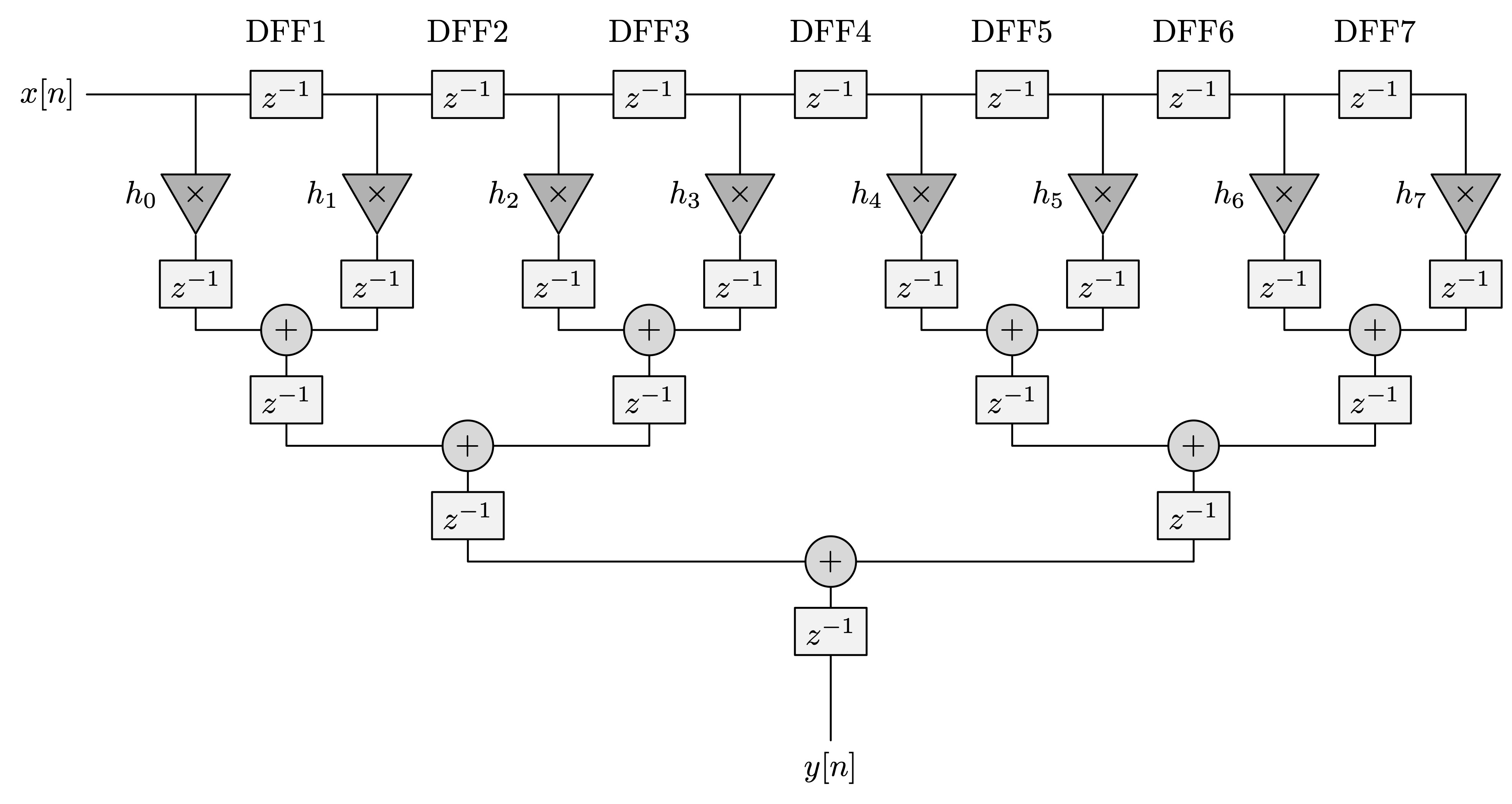
Code
\documentclass[border = 3pt, tikz]{standalone}
% Packages
\usepackage{tikz}
\usetikzlibrary{calc, shapes.geometric}
% Defaults
% Thicker Lines
\tikzset{every path/.append style=semithick}
% Triangle Node
\tikzset{
triangle/.style = {
fill=blue!20,
regular polygon,
regular polygon sides=3,
rotate=180
}
}
% D Flip-Flop Node
\newcommand{\DFF}[3]{%
\node (#2) at (#1) [draw, fill = black!5, minimum width=1, minimum height=1] {$z^{-1}$};%
\node[shift={(0,0.7)}] at (#1) {DFF#3};
}
\newcommand{\DFFnoLabel}[2]{%
\node (#2) at (#1) [draw, fill = black!5, minimum width=1, minimum height=1] {$z^{-1}$};%
}
% Adder Node
\newcommand{\Adder}[2]{%
\node (#2) at (#1) [draw, circle, fill = black!15, inner sep=2pt, minimum size=3pt] {$\mathbf+$}%
}
% Multiplier Node
\newcommand{\Multiplier}[3]{%
\node (#2) at (#1) [draw, triangle, fill = black!30, inner sep=0.5pt, minimum size=3pt] {$\mathbf\times$};%
\node[shift={(-0.6,0)}] at (#1) {$h_{#3}$}
}
% Constants
\def\x{2} % x distance
\def\in_out_x{1.2} % distance between last component and input, output
\def\y{2.2} % y distance
\def\num{7} % number of coefficients (2^x - 1, x = 2, 3, 4, ...)
\begin{document}
\begin{tikzpicture}[line cap = round, line join = round]
% Coordinates
\coordinate (Input) at (-6,4);
% Multipliers & 1st Row of DFFs
\foreach \i [evaluate=\i as \index using int(\num-\i)] in {0, 1, ..., \num} {
\draw ($(Input) + (\in_out_x+\x*\i,0)$) -- ++(0,-0.5*\y) coordinate (h\i);
%
\Multiplier{h\i}{mul\i}{\i};
%
\draw (mul\i) -- ++(0, -0.2*\y) coordinate (MUL\i);
%
% \DFF{MUL\i}{DFF-1\i};
\coordinate (DFF-1\i) at (MUL\i);
}
% Adder & DFF Tree
\coordinate (start) at ($(DFF-10) + (0.5*\x, -0.33*\y)$);
\pgfmathsetmacro{\levelmax}{int(ceil(log2(\num+1)-1))}
\foreach \level in {0, ..., \levelmax} {
%
\pgfmathsetmacro{\dis}{2^(\level)-1}
\pgfmathsetmacro{\disy}{\level};
%
\coordinate (start\level) at ($(start) + (\dis*\x, -0.13*\disy*\y)$);
%
\pgfmathsetmacro{\vertexmax}{2^(\levelmax-\level)-1};
%
\foreach \vertex in {0, ..., \vertexmax} {
%
\pgfmathsetmacro{\disx}{2*\vertex*2^(\level)};
\pgfmathsetmacro{\disy}{\level};
\coordinate (vertex\level\vertex) at ($(start\level) + (\disx*\x, -0.2*\disy*\y)$);
\Adder{vertex\level\vertex}{adder\level\vertex};
%
\node[inner sep=8pt] (DFF\level\vertex) at ($(adder\level\vertex)$) {};
% Connecting Vertexes
\pgfmathsetmacro{\downleft}{int(2*\vertex)};
\pgfmathsetmacro{\downright}{int(\downleft+1)};
\pgfmathsetmacro{\downlevel}{int(\level-1)};
\draw (DFF\downlevel\downleft) -- ++(0,-0.33*\y) -- (adder\level\vertex);
\draw (DFF\downlevel\downright) -- ++(0,-0.33*\y) -- (adder\level\vertex);
}
}
% From Input to Last Multiplier
\draw (Input) -- ++($(\in_out_x,0) + (\num*\x,0)$);
% DFFs on Input Line
\pgfmathsetmacro{\dffnum}{\num-1}
\foreach \i in {0, 1, ..., \dffnum} {
\coordinate (DFF_in) at ($(Input) + (\in_out_x+\x*\i + 0.5*\x,0)$);
%
\pgfmathsetmacro{\inext}{int(\i+1)};
\DFF{DFF_in}{DFF_in\i}{\inext};
}
% From Last Adder to Output
\draw (DFF\levelmax0) -- ++(0,-\in_out_x) coordinate (Output);
% Nodes for Input and Output
\node[left] at (Input) {$x[n]$};
\node[below] at (Output) {$y[n]$};
\end{tikzpicture}
\def\x{2} % clock length
\def\y{0.6} % clock height
\def\num{4} % number of clock periods
\def\spacey{1.2} % space between waveforms
\def\spacex{0.8} % space between waveforms labels
\begin{tikzpicture}[line cap = round, line join = round]
% Coordinates
\coordinate (start) at (-6,0);
% Time Axis
\draw[-latex] (start) -- ++(\num*2*\x + 2*\x,0) node [shift={(0,-0.5)}] {time};
% Clock
\coordinate (start0) at ($(start) + (-2*\x,0)$);
\foreach \i in {1,2,...,\num} {
\pgfmathsetmacro{\iprev}{\i-1}
\coordinate (start\i) at ($(start\iprev) + (2*\x,0)$);
%
\draw [thick] (start\i) -- ++(\x,0) -- ++(0,\y) -- ++(\x,0) --++(0,-\y);
% clk Up - Down
\node[shift = {(\x,-0.6*\y)}] (clkl\i) at (start\i) {$\uparrow$};
\node[shift = {(2*\x,-0.6*\y)}] (clkr\i) at (start\i) {$\downarrow$};
\node at ($(clkl\i)!0.5!(clkr\i)$) {\i};
}
\pgfmathsetmacro{\numnext}{int(\num+1)}
\coordinate (start\numnext) at ($(start\num) + (2*\x,0)$);
\draw[thick] (start\numnext) -- ++(\x,0) -- ++(0,\y);
% Nodes
% Reset
\pgfmathsetmacro{\numrst}{\num-1};
\coordinate (start_rst) at ($(start) + (0, \spacey)$);
\draw (start_rst) -- ++(\num*2*\x,0);
\draw[thick]
($(start_rst) + (0,\y)$) -- ++(2*\x,0)
-- ++(0, -\y)
-- ++ (\numrst*2*\x, 0)
-- ++ (\x, 0);
% Input
\pgfmathsetmacro{\numrst}{\num-1};
% start
\draw[thick] ($(start) + (0, 2*\spacey)$) -- ++(2*\x,0) coordinate (start0);
\draw (start0) -- ++(\num*2*\x - \x,0);
% recursive drawing
\foreach \n in {1,2,...,3} {
\pgfmathsetmacro{\nprev}{int(\n-1)};
\draw[thick]
(start\nprev) -- ++(0,\y) coordinate (xl\n)
-- ++(2*\x,0) coordinate (xr\n)
-- ++(0,-\y) coordinate (start\n);
\node (x\n) at ($(xl\n)!0.5!(xr\n) - (0,0.5*\y)$) {\small $x[\nprev]$};
}
\draw[thick] (xr3) -- +(\x,0);
% Output
\pgfmathsetmacro{\numrst}{\num-1};
% start
\draw[thick] ($(start) + (0, 3*\spacey)$) -- ++(3*\x,0) coordinate (start0);
\draw (start0) -- ++(\num*2*\x - 2*\x,0);
% recursive drawing
\foreach \n in {1,2,...,3} {
\pgfmathsetmacro{\nprev}{int(\n-1)};
\draw[thick]
(start\nprev) -- ++(0,\y) coordinate (yl\n)
-- ++(2*\x,0) coordinate (yr\n)
-- ++(0,-\y) coordinate (start\n);
\coordinate (y\n) at ($(yl\n)!0.5!(yr\n) - (0,0.5*\y)$);
}
% Nodes
\node at (y1) {\small $h_0x[0]$};
\node at (y2) {\small $h_0x[1] + h_1x_[0]$};
\node at (y3) {\small $h_0x[2] + h_1x[1] + h_2x[0]$};
% DFF1
% start
\draw[thick] ($(start) + (0, 4*\spacey)$) -- ++(3*\x,0) coordinate (start0);
\draw (start0) -- ++(\num*2*\x - 2*\x,0);
% recursive drawing
\foreach \n in {1,2,...,3} {
\pgfmathsetmacro{\nprev}{int(\n-1)};
\draw[thick]
(start\nprev) -- ++(0,\y) coordinate (DFF7l\n)
-- ++(2*\x,0) coordinate (DFF7r\n)
-- ++(0,-\y) coordinate (start\n);
\coordinate (DFF7\n) at ($(DFF7l\n)!0.5!(DFF7r\n) - (0,0.5*\y)$);
}
% Nodes
\node at (DFF71) {\small $x[0]$};
\node at (DFF72) {\small $x[1]$};
\node at (DFF73) {\small $\cdots$};
% DFF2
% start
\draw[thick] ($(start) + (0, 5*\spacey)$) -- ++(5*\x,0) coordinate (start0);
\draw (start0) -- ++(\num*2*\x - 4*\x,0);
% recursive drawing
\foreach \n in {1,...,2} {
\pgfmathsetmacro{\nprev}{int(\n-1)};
\draw[thick]
(start\nprev) -- ++(0,\y) coordinate (DFF6l\n)
-- ++(2*\x,0) coordinate (DFF6r\n)
-- ++(0,-\y) coordinate (start\n);
\coordinate (DFF6\n) at ($(DFF6l\n)!0.5!(DFF6r\n) - (0,0.5*\y)$);
}
% Nodes
\node at (DFF61) {\small $x[0]$};
\node at (DFF62) {\small $\cdots$};
% Nodes
\node at ($(start) + (-\spacex, 0.5*\y)$) {clk}; % clk
\node at ($(start) + (-\spacex, 0.5*\y + \spacey)$) {rst}; % rst
\node at ($(start) + (-\spacex, 0.5*\y + 2*\spacey)$) {$x[n]$}; % x[n]
\node at ($(start) + (-\spacex, 0.5*\y + 3*\spacey)$) {$y[n]$}; % y[n]
\node at ($(start) + (-\spacex, 0.5*\y + 4*\spacey)$) {DFF1}; % DFF1
\node at ($(start) + (-\spacex, 0.5*\y + 5*\spacey)$) {DFF2}; % DFF2
\end{tikzpicture}
% Constants
\def\x{2} % x distance
\def\in_out_x{1.2} % distance between last component and input, output
\def\y{2.2} % y distance
\def\num{7} % number of coefficients (2^x - 1, x = 2, 3, 4, ...)
\begin{tikzpicture}[line cap = round, line join = round]
% Coordinates
\coordinate (Input) at (-6,4);
% Multipliers & 1st Row of DFFs
\foreach \i [evaluate=\i as \index using int(\num-\i)] in {0, 1, ..., \num} {
\draw ($(Input) + (\in_out_x+\x*\i,0)$) -- ++(0,-0.5*\y) coordinate (h\i);
%
\Multiplier{h\i}{mul\i}{\i};
%
\draw (mul\i) -- ++(0, -0.45*\y) coordinate (MUL\i);
%
\DFFnoLabel{MUL\i}{DFF-1\i};
}
% Adder & DFF Tree
\coordinate (start) at ($(DFF-10) + (0.5*\x, -0.23*\y)$);
\pgfmathsetmacro{\levelmax}{int(ceil(log2(\num+1)-1))}
\foreach \level in {0, ..., \levelmax} {
%
\pgfmathsetmacro{\dis}{2^(\level)-1}
\pgfmathsetmacro{\disy}{\level};
%
\coordinate (start\level) at ($(start) + (\dis*\x, -0.23*\disy*\y)$);
%
\pgfmathsetmacro{\vertexmax}{2^(\levelmax-\level)-1};
%
\foreach \vertex in {0, ..., \vertexmax} {
%
\pgfmathsetmacro{\disx}{2*\vertex*2^(\level)};
\pgfmathsetmacro{\disy}{\level};
\coordinate (vertex\level\vertex) at ($(start\level) + (\disx*\x, -0.35*\disy*\y)$);
\Adder{vertex\level\vertex}{adder\level\vertex};
%
\node[inner sep=8pt] (VERTEX\level\vertex) at ($(adder\level\vertex) + (0,-0.35*\y)$) {};
\DFFnoLabel{VERTEX\level\vertex}{DFF\level\vertex};
% Connect Adder to DFF
\draw (adder\level\vertex) -- (DFF\level\vertex);
% Connecting Vertexes
\pgfmathsetmacro{\downleft}{int(2*\vertex)};
\pgfmathsetmacro{\downright}{int(\downleft+1)};
\pgfmathsetmacro{\downlevel}{int(\level-1)};
\draw (DFF\downlevel\downleft) -- ++(0,-0.23*\y) -- (adder\level\vertex);
\draw (DFF\downlevel\downright) -- ++(0,-0.23*\y) -- (adder\level\vertex);
}
}
% From Input to Last Multiplier
\draw (Input) -- ++($(\in_out_x,0) + (\num*\x,0)$);
% DFFs on Input Line
\pgfmathsetmacro{\dffnum}{\num-1}
\foreach \i in {0, 1, ..., \dffnum} {
\coordinate (DFF_in) at ($(Input) + (\in_out_x+\x*\i + 0.5*\x,0)$);
%
\pgfmathsetmacro{\inext}{int(\i+1)};
\DFF{DFF_in}{DFF_in\i}{\inext};
}
% From Last Adder to Output
\draw (DFF\levelmax0) -- ++(0,-\in_out_x) coordinate (Output);
% Nodes for Input and Output
\node[left] at (Input) {$x[n]$};
\node[below] at (Output) {$y[n]$};
\end{tikzpicture}
\end{document}


