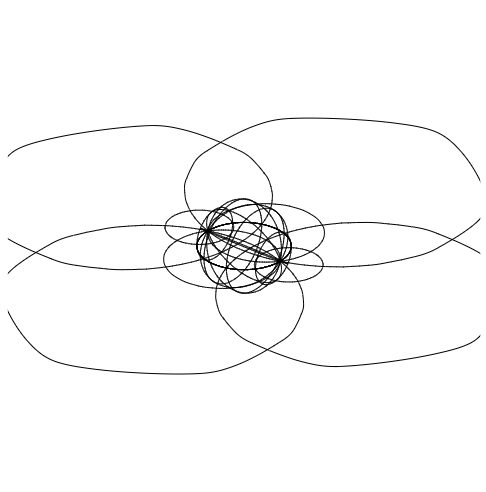
If you take the stereographic projection of a mesh sphere, you obtain Steiner circles.
Interestingly, the map of any inscribed circle of the sphere under stereographic projection is a perfect circle on the plane.
Unfortunately, due to the low sampling size, the smooth option can be a bit botched sometimes.
The code is parameterized so that the user can specify Euler angle rotations of the sphere, and see the resulting stereographic projection on the plane.
If a line goes near the north pole, we omit it by setting the opacity to zero.
There are other workarounds, but they require using a conditional in a for loop, and I wanted to use the smooth option.
For example, this animation shows the sphere undergoing a rotation which is based on all three angles changing differently:
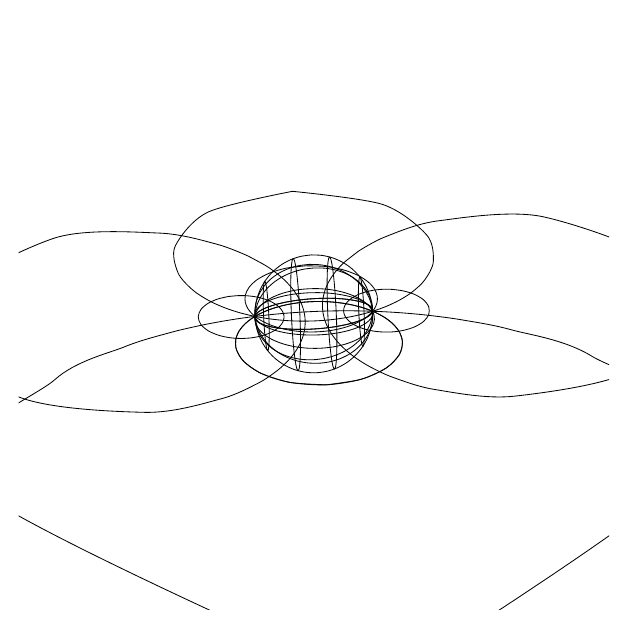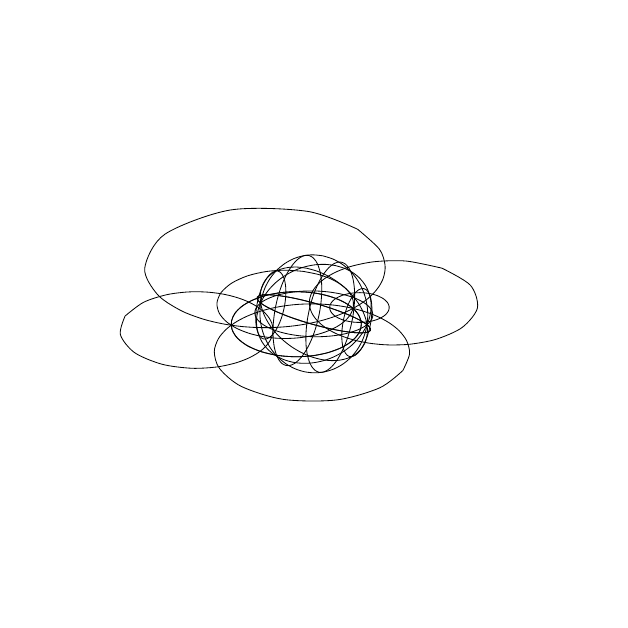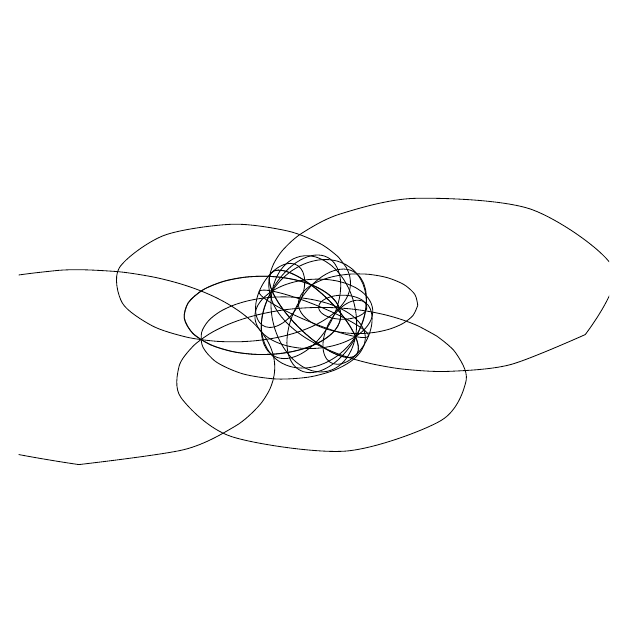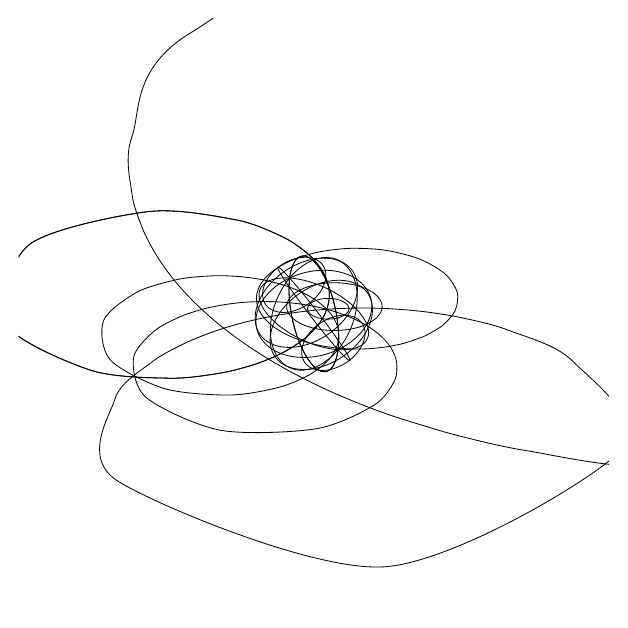
Try changing the values of \zrotationa, \yrotation and \zrotationb for yourself!
\documentclass[
tikz
,border = 3.14mm
]{standalone}
\usepackage{tikz-3dplot}
\pgfmathdeclarefunction{sphereX}{2}{%
% #1 - longitude
% #2 - latitude
\pgfmathparse{cos(#2)*cos(#1)}%
}
\pgfmathdeclarefunction{sphereY}{2}{%
\pgfmathparse{cos(#2)*sin(#1)}%
}
\pgfmathdeclarefunction{sphereZ}{2}{%
\pgfmathparse{sin(#2)}%
}
% https://tex.stackexchange.com/a/736767/319072
\pgfmathdeclarefunction{tdplottransformrotmainX}{6}{%
% #1 - Z rotation
% #2 - Y rotation
% #3 - Z rotation
% #4 - x value
% #5 - y value
% #6 - z value
\pgfmathparse{
(
(
sin(#1) * cos(#2) * cos(#3) +
cos(#1) * sin(#3)
) * #4 +
(
-sin(#1) * cos(#2) * sin(#3) +
cos(#1) * cos(#3)
) * #5 +
sin(#1) * sin(#2) * #6
) * -1
}%
}
\pgfmathdeclarefunction{tdplottransformrotmainY}{6}{%
\pgfmathparse{
(
cos(#1) * cos(#2) * cos(#3) -
sin(#1) * sin(#3)
) * #4 +
(
-cos(#1) * cos(#2) * sin(#3) -
sin(#1) * cos(#3)
) * #5 +
cos(#1) * sin(#2) * #6
}%
}
\pgfmathdeclarefunction{tdplottransformrotmainZ}{6}{%
\pgfmathsetmacro\tdplottransformrotmainZtemp{
-sin(#2) * cos(#3) * #4 +
sin(#2) * sin(#3) * #5 +
cos(#2) * #6
}%
\pgfmathparse{%
\tdplottransformrotmainZtemp > 0.995%
}%
\ifnum\pgfmathresult=1%
\xdef\opacity{0}%
\fi%
\let\pgfmathresult\tdplottransformrotmainZtemp%
}
\pgfmathdeclarefunction{stereographicprojection}{2}{%
% #1 - the x or y value of the input
% #2 - the z value of the input
% Returns the x or y value of the output
\pgfmathparse{#2 < 0.995}%
\ifnum\pgfmathresult=1%
\pgfmathparse{#1 / (1 - #2)}%
\else%
\pgfmathparse{#1 / (1 - 0.995)}%
\fi%
}
\pgfmathsetmacro{\azimuth}{130} % viewing azimuth
\pgfmathsetmacro{\elevation}{30} % viewing elevation
\pgfmathsetmacro{\zrotationa}{0} % Z1 rotation of sphere
\pgfmathsetmacro{\yrotation}{90} % Y rotation of sphere
\pgfmathsetmacro{\zrotationb}{0} % Z2 rotation of sphere
\begin{document}
\tdplotsetmaincoords{90-\elevation}{\azimuth}
\begin{tikzpicture}[tdplot_main_coords]
\clip[tdplot_screen_coords] (-5,-5) rectangle (5,5);
\pgfmathsetmacro{\startlongitude}{-90}
\pgfmathsetmacro{\endlongitude}{90}
\pgfmathsetmacro{\sampleslongitude}{5}
\pgfmathsetmacro{\steplongitude}{
(\endlongitude - \startlongitude) /
\sampleslongitude
}
\foreach \longitude[parse = true] in {%
\startlongitude%
,\startlongitude + \steplongitude%
,...%
,\endlongitude%
} {
\xdef\opacity{1}
\draw[
smooth
,domain = 0:360
,samples = 35
,variable = \latitude
] plot (
{
tdplottransformrotmainX(
\zrotationa,\yrotation,\zrotationb
,sphereX(\longitude,\latitude)
,sphereY(\longitude,\latitude)
,sphereZ(\longitude,\latitude)
)
}
,{
tdplottransformrotmainY(
\zrotationa,\yrotation,\zrotationb
,sphereX(\longitude,\latitude)
,sphereY(\longitude,\latitude)
,sphereZ(\longitude,\latitude)
)
}
,{
tdplottransformrotmainZ(
\zrotationa,\yrotation,\zrotationb
,sphereX(\longitude,\latitude)
,sphereY(\longitude,\latitude)
,sphereZ(\longitude,\latitude)
)
}
);
\draw[
smooth
,domain = 0:360
,samples = 35
,variable = \latitude
,opacity = \opacity
] plot (
{
stereographicprojection(
tdplottransformrotmainX(
\zrotationa,\yrotation,\zrotationb
,sphereX(\longitude,\latitude)
,sphereY(\longitude,\latitude)
,sphereZ(\longitude,\latitude)
)
,tdplottransformrotmainZ(
\zrotationa,\yrotation,\zrotationb
,sphereX(\longitude,\latitude)
,sphereY(\longitude,\latitude)
,sphereZ(\longitude,\latitude)
)
)
}
,{
stereographicprojection(
tdplottransformrotmainY(
\zrotationa,\yrotation,\zrotationb
,sphereX(\longitude,\latitude)
,sphereY(\longitude,\latitude)
,sphereZ(\longitude,\latitude)
)
,tdplottransformrotmainZ(
\zrotationa,\yrotation,\zrotationb
,sphereX(\longitude,\latitude)
,sphereY(\longitude,\latitude)
,sphereZ(\longitude,\latitude)
)
)
}
);
% Going forward, we interchange latitude and longitude to
% find orthogonal trajectories on the sphere and on the plane.
\xdef\opacity{1}
\draw[
smooth
,domain = 0:360
,samples = 35
,variable = \latitude
] plot (
{
tdplottransformrotmainX(
\zrotationa,\yrotation,\zrotationb
,sphereX(\latitude,\longitude)
,sphereY(\latitude,\longitude)
,sphereZ(\latitude,\longitude)
)
}
,{
tdplottransformrotmainY(
\zrotationa,\yrotation,\zrotationb
,sphereX(\latitude,\longitude)
,sphereY(\latitude,\longitude)
,sphereZ(\latitude,\longitude)
)
}
,{
tdplottransformrotmainZ(
\zrotationa,\yrotation,\zrotationb
,sphereX(\latitude,\longitude)
,sphereY(\latitude,\longitude)
,sphereZ(\latitude,\longitude)
)
}
);
\draw[
smooth
,domain = 0:360
,samples = 35
,variable = \latitude
,opacity = \opacity
] plot (
{
stereographicprojection(
tdplottransformrotmainX(
\zrotationa,\yrotation,\zrotationb
,sphereX(\latitude,\longitude)
,sphereY(\latitude,\longitude)
,sphereZ(\latitude,\longitude)
)
,tdplottransformrotmainZ(
\zrotationa,\yrotation,\zrotationb
,sphereX(\latitude,\longitude)
,sphereY(\latitude,\longitude)
,sphereZ(\latitude,\longitude)
)
)
}
,{
stereographicprojection(
tdplottransformrotmainY(
\zrotationa,\yrotation,\zrotationb
,sphereX(\latitude,\longitude)
,sphereY(\latitude,\longitude)
,sphereZ(\latitude,\longitude)
)
,tdplottransformrotmainZ(
\zrotationa,\yrotation,\zrotationb
,sphereX(\latitude,\longitude)
,sphereY(\latitude,\longitude)
,sphereZ(\latitude,\longitude)
)
)
}
);
}
\end{tikzpicture}
\end{document}


