Stereographic Projection in Spherical Coordinates

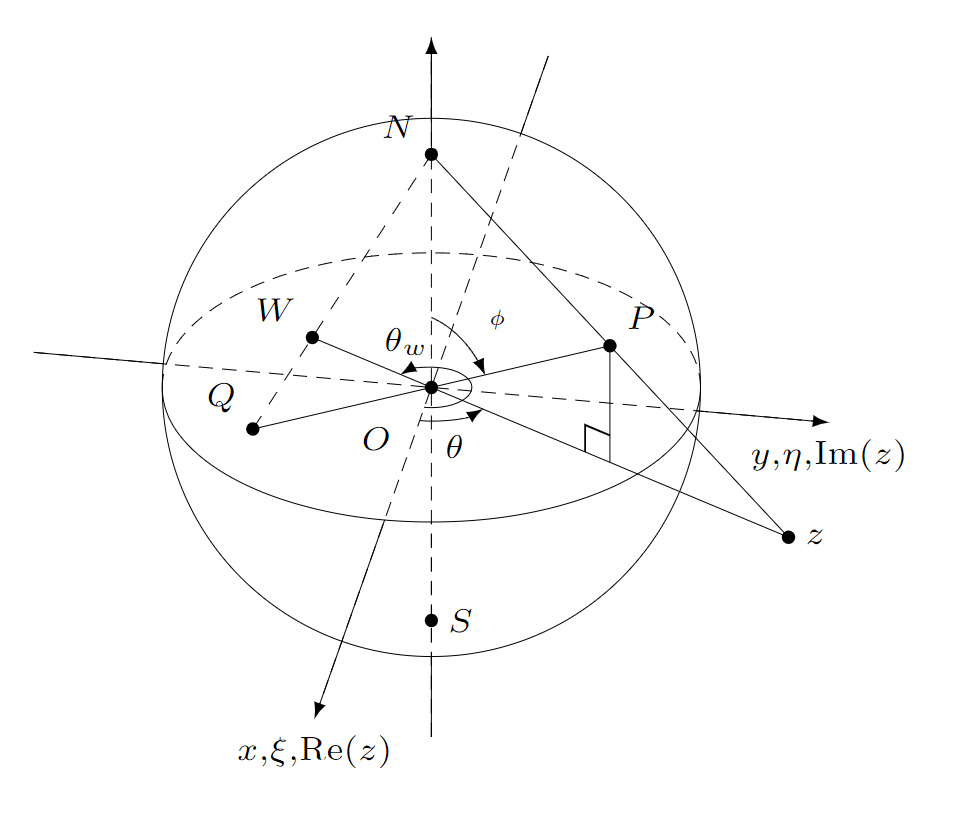
The stereographic projection of two antipodal points:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
\documentclass[
    tikz
    ,border = 3.14mm
]{standalone}
\usepackage{tikz-3dplot}
\usetikzlibrary{
    arrows.meta
    ,angles
}
\pgfmathdeclarefunction{sphereX}{2}{%
    % #1  - longitude
    % #1  - latitude
    \pgfmathparse{cos(#2) * cos(#1)}%
}
\pgfmathdeclarefunction{sphereY}{2}{%
    \pgfmathparse{cos(#2) * sin(#1)}%
}
\pgfmathdeclarefunction{sphereZ}{2}{%
    \pgfmathparse{sin(#2)}%
}
\pgfmathdeclarefunction{stereographicprojection}{2}{%
    \pgfmathparse{#1 / (1 - #2)}%
}
\pgfmathsetmacro{\azimuth}{100}
\pgfmathsetmacro{\elevation}{30}
\pgfmathsetmacro{\longitude}{60}
\pgfmathsetmacro{\latitude}{30}
\begin{document}
    \pgfmathsetmacro{\scale}{2}
    \tdplotsetmaincoords{90-\elevation}{\azimuth}
    \begin{tikzpicture}[tdplot_main_coords,very thin]
        % x, y and z axes (pre-clip)
        \draw[-latex] 
            (-2.5*\scale,0,0) -- (2.5*\scale,0,0)
            node[pos=1,below] 
            {$\scriptstyle x,\xi,\mbox{\scriptsize Re}(z)$};
        \draw[-latex] 
            (0,-1.5*\scale,0) -- (0,1.5*\scale,0);
        \draw[-latex] 
            (0,0,-1.5*\scale) -- (0,0,1.5*\scale);
        \begin{scope}
 
 
הההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההה
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX