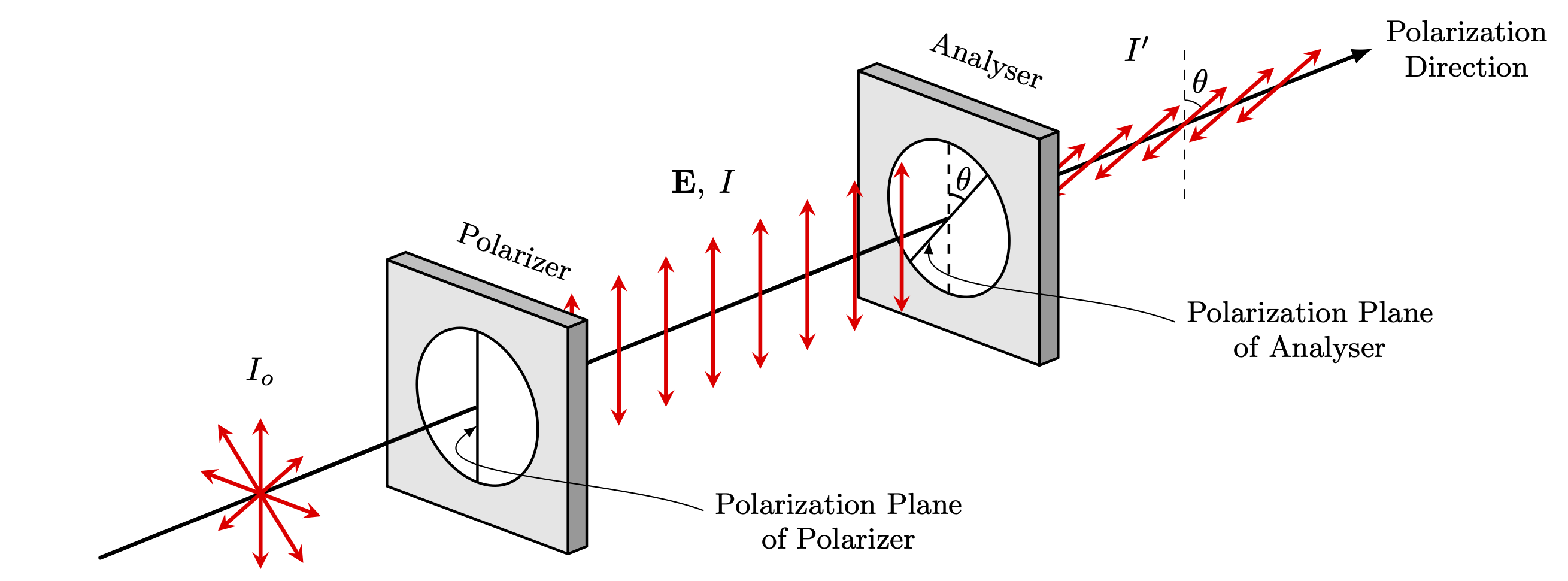
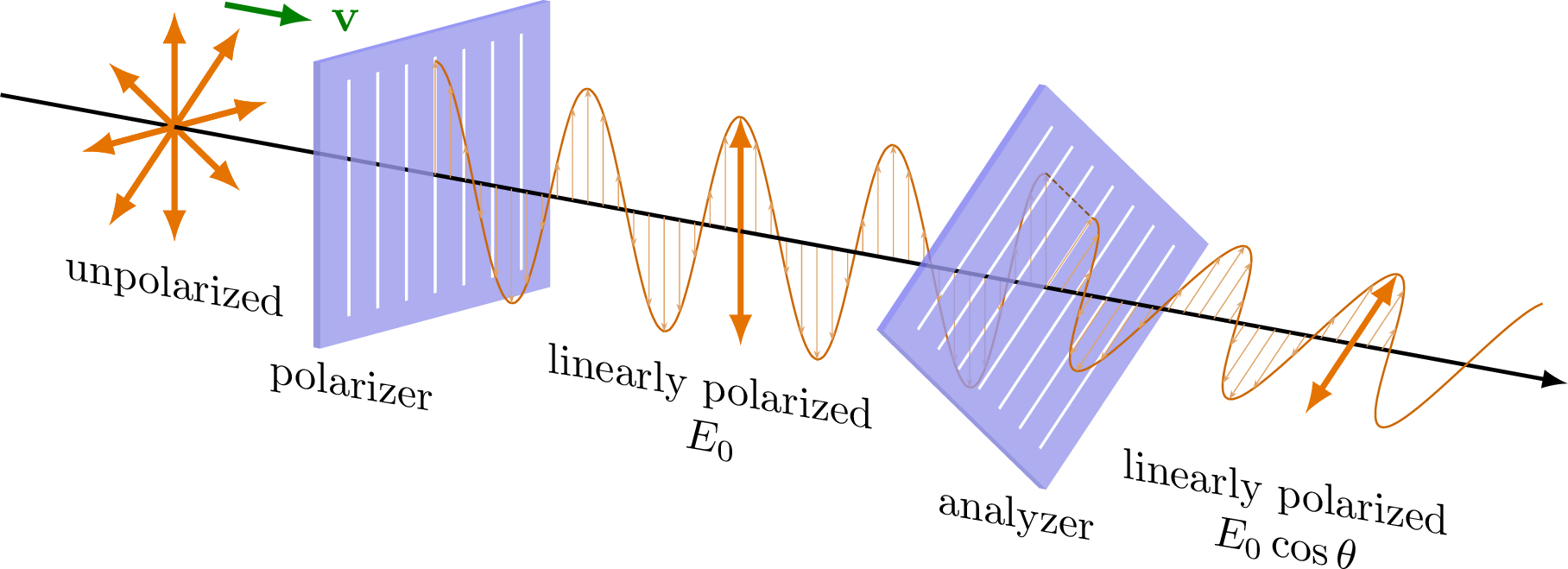
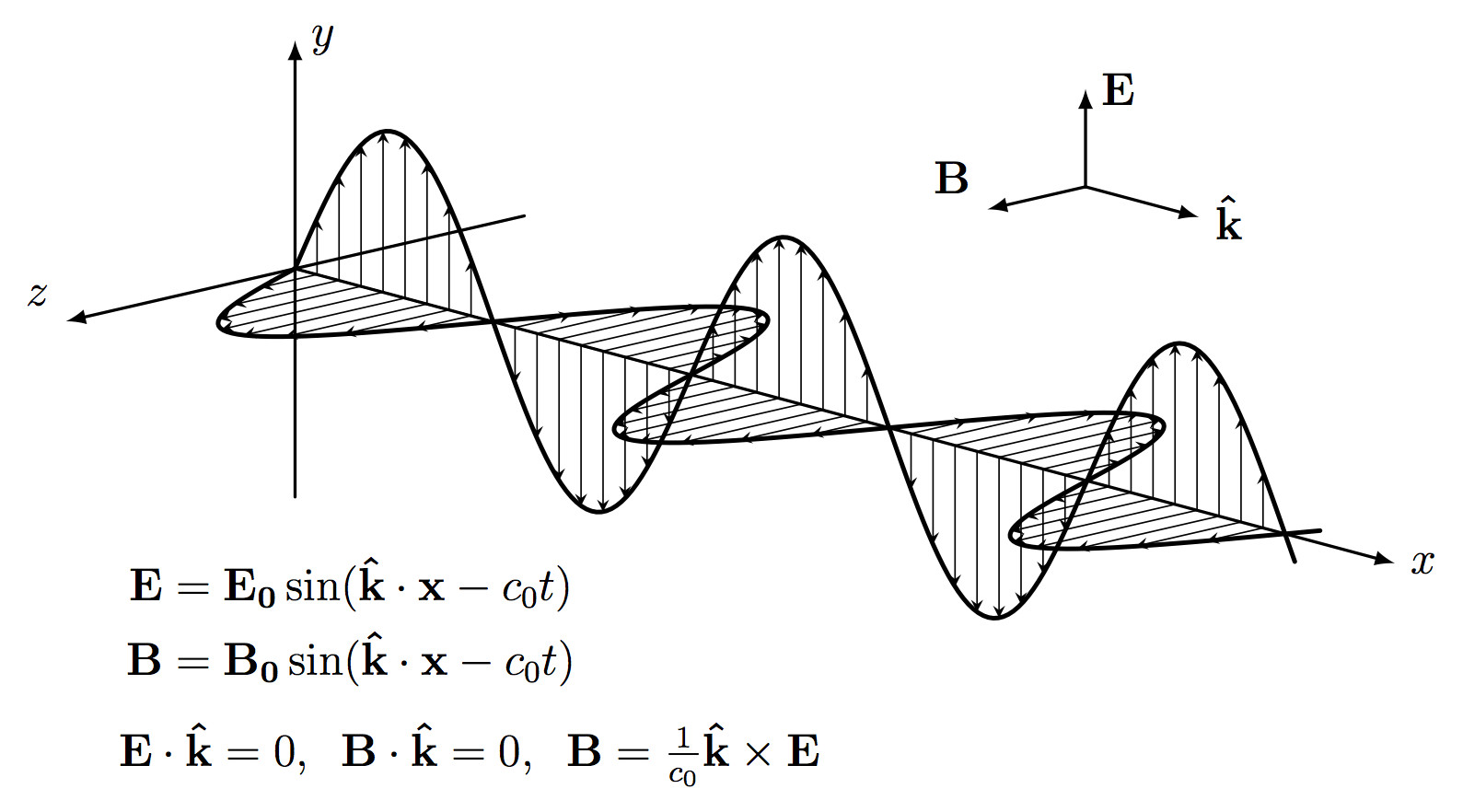
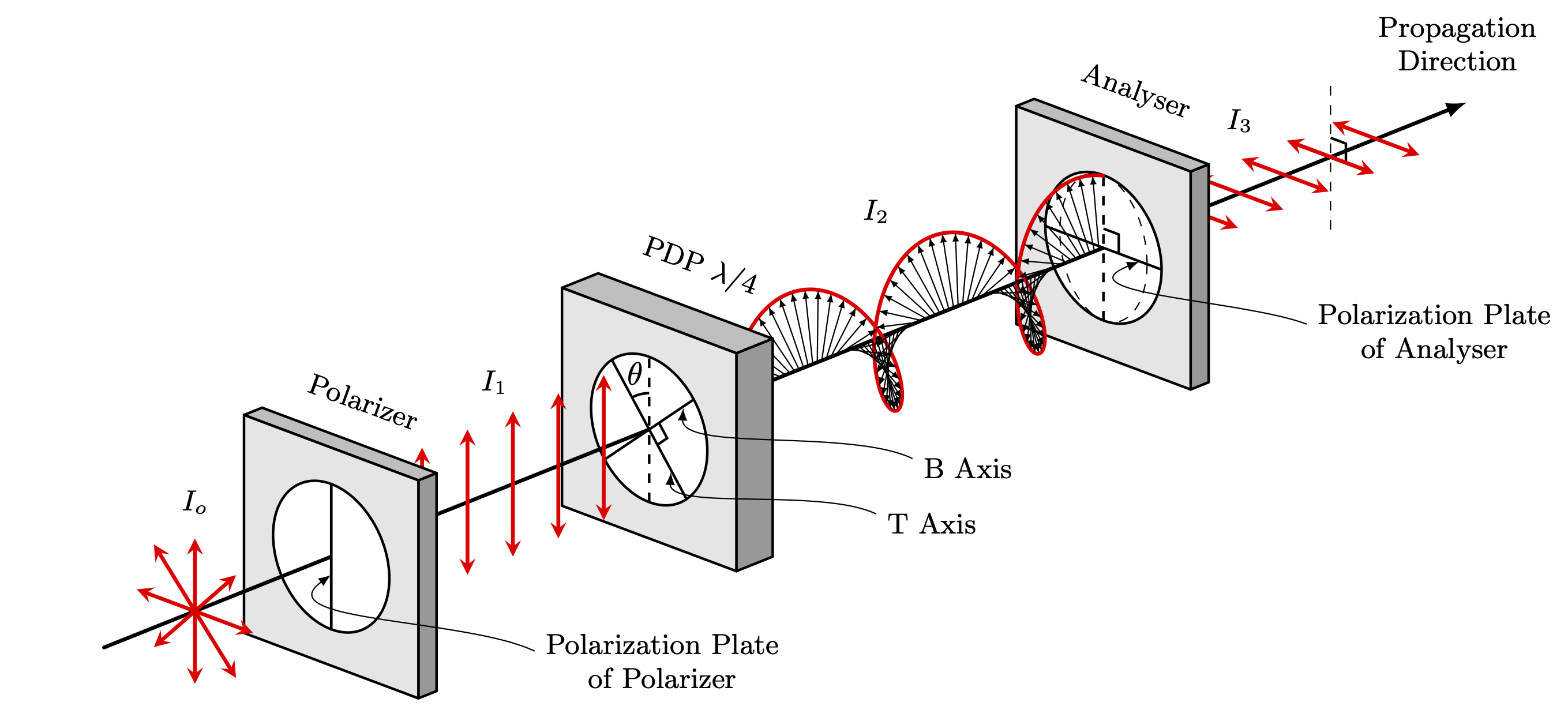
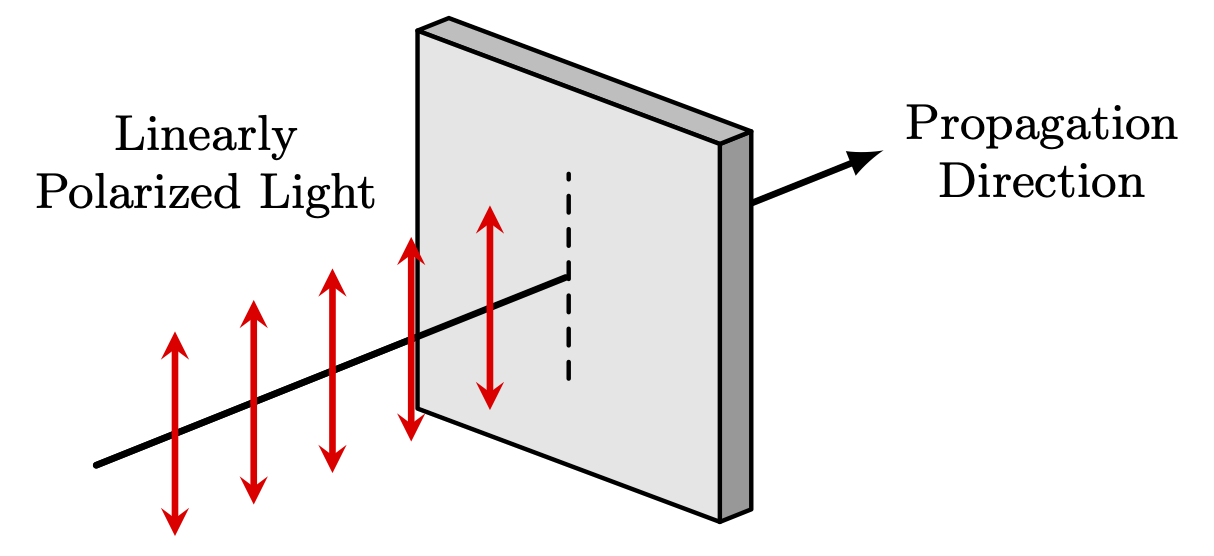
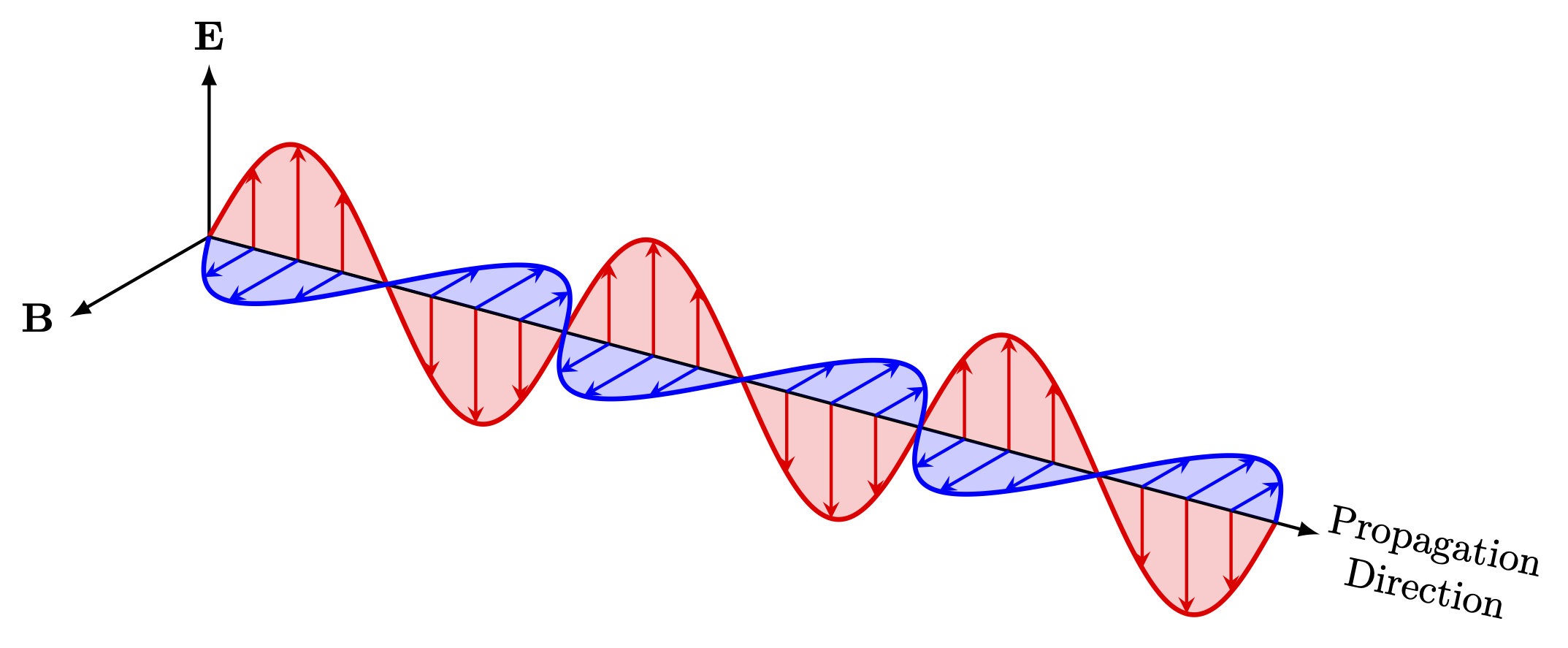
Edit and compile if you like:
\documentclass[border=3pt]{standalone}
% Drawing
\usepackage{tikz}
% Tikz Library
\usetikzlibrary{3d, shapes.multipart, angles, quotes}
% Tikz Styles
\tikzset{>=latex}
\tikzset{axis/.style={black, very thick, ->}}
\tikzset{ef/.style={very thick, red}}
\tikzset{vec/.style={black, -{Latex[length=0.8mm]}}}
\tikzset{every text node part/.style={align=center}}
% Newcommand
%% Polar Coordinates Line from (0,0 to (r, theta)
\newcommand{\cdraw}[2]{\draw[very thick, -stealth, red] (0,0) -- ({#1*cos(#2)}, {#1*sin(#2)});}
%% Polarizer
\newcommand{\polarizer}[2]{%
\begin{scope}[canvas is xz plane at y=1.2]
\draw[line join=round, thick, fill=black!40] (#1,-1.2) rectangle (#1+0.2,1.2);
\end{scope}
%
\begin{scope}[canvas is xy plane at z=1.2]
\draw[line join=round, thick, fill=black!25](#1,-1.2) rectangle (#1+0.2,1.2);
\end{scope}
%
\begin{scope}[canvas is yz plane at x=#1]
\draw[line join=round, thick, fill=black!10] (-1.2,-1.2) rectangle (1.2,1.2);
\draw[line join=round, thick, fill=white] (0,0) circle (0.8cm);
\draw[line join=round, thick] (-{0.8*cos(#2)}, -{0.8*sin(#2)}) -- ({0.8*cos(#2)},{0.8*sin(#2)});
\end{scope}
}
%% Analyser
\newcommand{\analizer}[2]{%
\begin{scope}[canvas is xz plane at y=1.2]
\draw[line join=round, thick, fill=black!40] (#1,-1.2) rectangle (#1+0.2,1.2);
\end{scope}
%
\begin{scope}[canvas is xy plane at z=1.2]
\draw[line join=round, thick, fill=black!25](#1,-1.2) rectangle (#1+0.2,1.2);
\end{scope}
%
\begin{scope}[canvas is yz plane at x=#1]
\draw[line join=round, thick, fill=black!10] (-1.2,-1.2) rectangle (1.2,1.2);
\draw[line join=round, thick, fill=white] (0,0) coordinate (B) circle (0.8cm);
\draw[line join=round, thick] (-{0.8*cos(#2)}, -{0.8*sin(#2)}) -- ({0.8*cos(#2)},{0.8*sin(#2)}) coordinate (A);
\draw[line join=round, dashed, thick] (0,-0.8) -- (0,0.8) coordinate (C);
\pic[line join=round, draw, thick, "$\theta$", angle radius=0.25cm, angle eccentricity=1.8] {angle = A--B--C};
\end{scope}
}
% Notation
\usepackage{amsmath}
\begin{document}
%Layers
\pgfdeclarelayer{layer1}
\pgfdeclarelayer{layer2}
\pgfdeclarelayer{layer3}
\pgfdeclarelayer{layer4}
\pgfdeclarelayer{layer5}
\pgfdeclarelayer{layer6}
\pgfdeclarelayer{layer7}
\pgfsetlayers{main, layer7, layer6, layer5, layer4, layer3, layer2, layer1}
\begin{tikzpicture}[x={(1cm,0.4cm)}, y={(8mm, -3mm)}, z={(0cm,1cm)}, line cap=round, line join=round]
% Main Axes
% \draw[->] (0,0,0) -- (12,0,0) node[right] {$x$};
% \draw[->] (0,0,0) -- (0,2,0) node[below left] {$y$};
% \draw[->] (0,0,0) -- (0,0,2) node[above] {$z$};
% Big Axis
\draw[axis] (-1,0,0) -- (12.5,0,0) node[right, black] {\small{Polarization}\\[-0.5mm]\small{Direction}};
% Polarizers
\begin{pgfonlayer}{layer1}
\polarizer{3}{90}
\end{pgfonlayer}
\begin{pgfonlayer}{layer3}
\analizer{8}{50}
\end{pgfonlayer}
% Polarizer and Analiyzer Nodes
\begin{scope}[canvas is yz plane at x=3]
\node[rotate=-20] at (0.5,1.8) {\small{Polarizer}};
\end{scope}
%
\begin{scope}[canvas is yz plane at x=8]
\node[rotate=-20] at (0.5,1.8) {\small{Analyser}};
\end{scope}
% Polarization Planes
\begin{pgfonlayer}{layer1}
\begin{scope}[canvas is xy plane at z=-0.2]
\draw[latex-] (3,0) to[out=160, in=270] (3,3) node[right, yshift=-3pt] {\small{Polarization Plane}\\[-0.5mm]\small{of Polarizer}};
\end{scope}
%
\begin{scope}[canvas is xy plane at z=-0.2]
\draw[latex-] (7.85,-0.07) to[out=130, in=270] (8,3) node[right, yshift=-3pt] {\small{Polarization Plane}\\[-0.5mm]\small{of Analyser}};
\end{scope}
\end{pgfonlayer}
% Electric Field
%% Physical Light
\begin{pgfonlayer}{layer1}
\begin{scope}[canvas is yz plane at x=0.7]
\foreach \i in {0,45,...,315}
{
\cdraw{0.8}{\i}
}
\end{scope}
\end{pgfonlayer}
%% Linear Polarization
\begin{pgfonlayer}{layer2}
\begin{scope}[canvas is yz plane at x=5.4]
\node at (0,1.4) {$\mathbf E, \: I$};
\end{scope}
\foreach \i in {3,3.5,...,7.5}
{
\begin{scope}[canvas is yz plane at x=\i]
\cdraw{0.8}{90}
\cdraw{0.8}{270}
\end{scope}
}
\end{pgfonlayer}
%% Slanted Linear Polarization
\begin{pgfonlayer}{layer4}
\begin{scope}[canvas is yz plane at x=10.5]
\draw[dashed] (0,-0.8) -- (0,0.8);
\coordinate (A) at ({0.8*cos(45)},{0.8*sin(45)});
\coordinate (B) at (0,0);
\coordinate (C) at (0,0.8);
\pic[draw, "$\theta$", angle radius=0.25cm, angle eccentricity=2, pic text options={xshift=-1pt}] {angle = A--B--C};
\end{scope}
\foreach \i in {8,8.5,...,11.5}
{
\begin{scope}[canvas is yz plane at x=\i]
\cdraw{0.8}{45}
\cdraw{0.8}{225}
\end{scope}
}
\end{pgfonlayer}
% Nodes
\node at (0.7,0,1.3) {$I_o$};
\node at (10,0,1) {$I'$};
% Refinements for 3D View
\begin{pgfonlayer}{layer1}
\draw[very thick] (1,0,0) -- (2.99,0,0);
\end{pgfonlayer}
\begin{pgfonlayer}{layer3}
\draw[very thick] (6,0,0) -- (7.99,0,0);
\end{pgfonlayer}
\end{tikzpicture}
\end{document}
Click to download: malus-law.tex
Open in Overleaf: malus-law.tex
This file is available on GitHub.
See more on the author page of Alexandros Tsagkaropolulos.