From Wikipedia:
A rotary encoder, also called a shaft encoder, is an electro-mechanical device that converts the angular position or motion of a shaft or axle to analog or digital output signals.
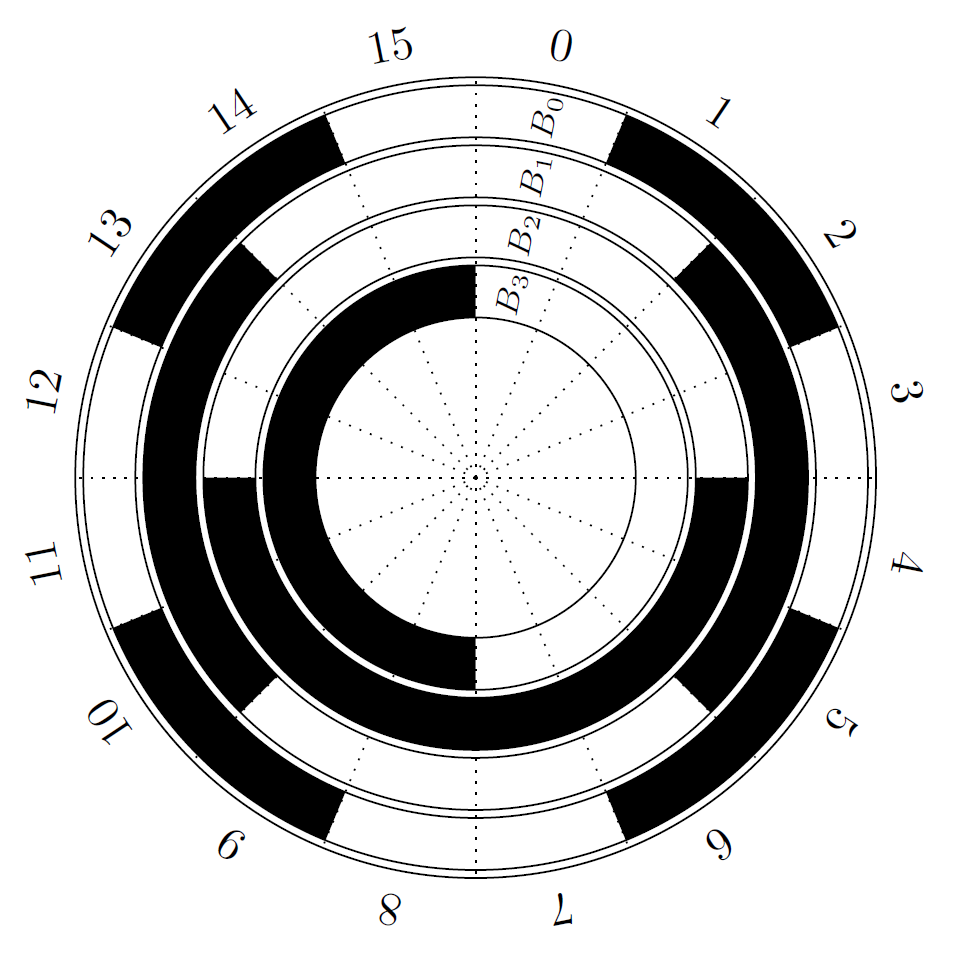
There are two main types of rotary encoder: absolute and incremental. The output of an absolute encoder indicates the current shaft position, making it an angle transducer. The output of an incremental encoder provides information about the motion of the shaft, which typically is processed elsewhere into information such as position, speed and distance.
The following TikZ picture by Germain Gondor (see also his Seven-segment display code) works with the Gray code.
Edit and compile if you like:
\documentclass[border=10pt]{standalone}\usepackage{tikz}\begin{document}\begin{tikzpicture}\def\R{3} % Radius\def\basea{22.5} % 360/(2^4)% Big circle and numbering\draw circle(\R);\foreach \x in {0,\basea, ..., 359}{\draw [dotted](0,0)--(\x:\R);} % draw radius\foreach \x in {0,...,15}{\pgfmathsetmacro\ang{-(\x+0.5)*\basea} % calculate position\node at({90-(\x+0.5)*\basea}:1.1*\R)[rotate=\ang]{\x};} % numbering% Circles\foreach \x in {40,53, 55,68,70,83,85,98} % Diameters{\draw circle({\x*\R/100});}% B3\fill (4*\basea:0.53*\R)arc(4*\basea:12*\basea:0.53*\R)--(12*\basea:0.40*\R)arc(12*\basea:4*\basea:0.40*\R)--cycle;% B2\fill (8*\basea:0.68*\R)arc(8*\basea:16*\basea:0.68*\R)--(16*\basea:0.55*\R)arc(16*\basea:8*\basea:0.55*\R)--cycle;% B1\foreach \x in {0,1}{\fill ({4*(1.5+\x*2)*\basea}:0.83*\R)arc({4*(1.5+\x*2)*\basea}:{4*(2.5+\x*2)*\basea}:0.83*\R)--({4*(2.5+\x*2)*\basea}:0.70*\R)arc({4*(2.5+\x*2)*\basea}:{4*(1.5+\x*2)*\basea}:0.70*\R)--cycle;}% B0\foreach \x in {0,...,3}{\fill ({2*(0.5+\x*2)*\basea}:0.98*\R)arc({2*(0.5+\x*2)*\basea}:{2*(1.5+\x*2)*\basea}:0.98*\R)--({2*(1.5+\x*2)*\basea}:0.85*\R)arc({2*(1.5+\x*2)*\basea}:{2*(0.5+\x*2)*\basea}:0.85*\R)--cycle;}
Click to download: absolute-rotary-encoder.tex • absolute-rotary-encoder.pdf
Open in Overleaf: absolute-rotary-encoder.tex