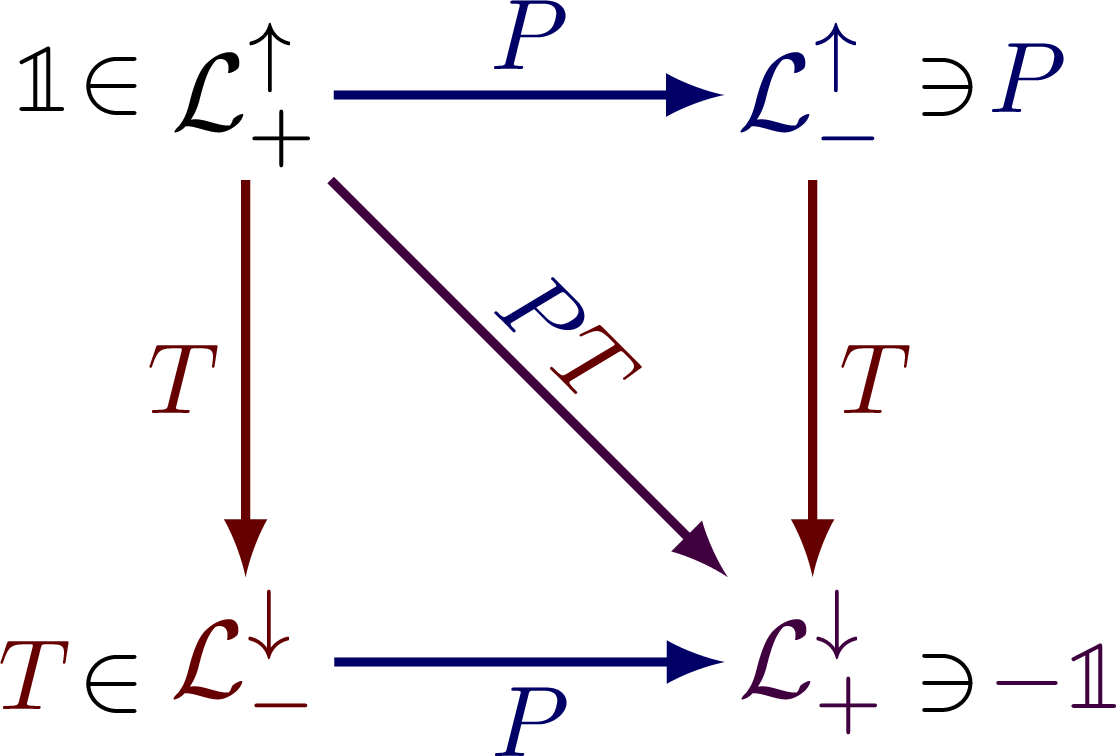
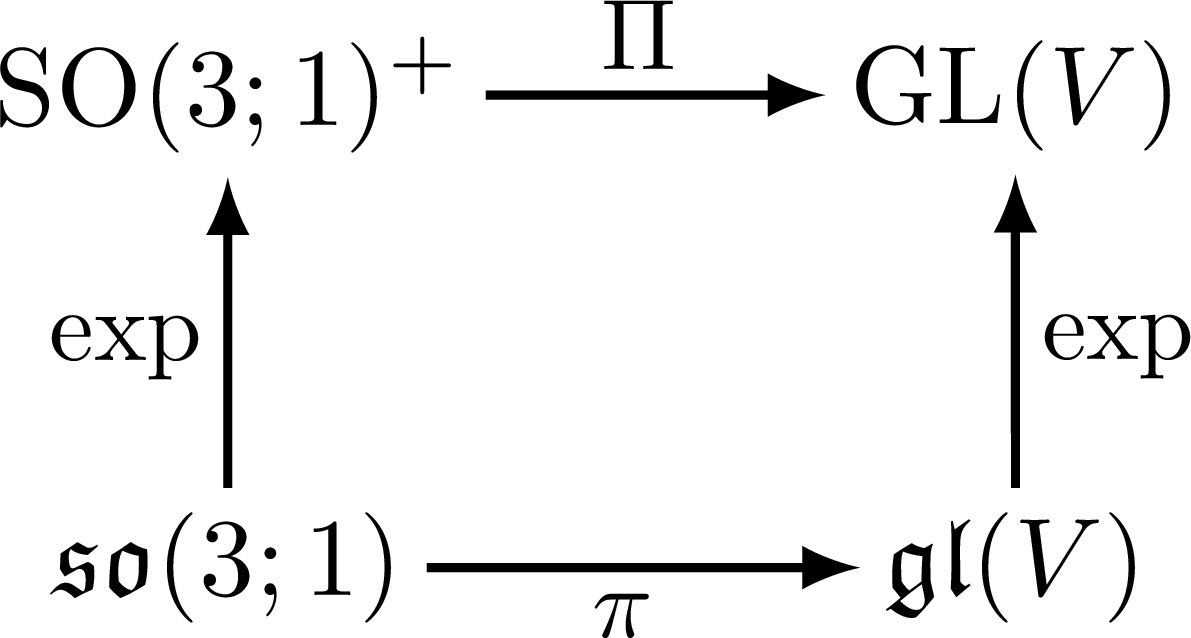
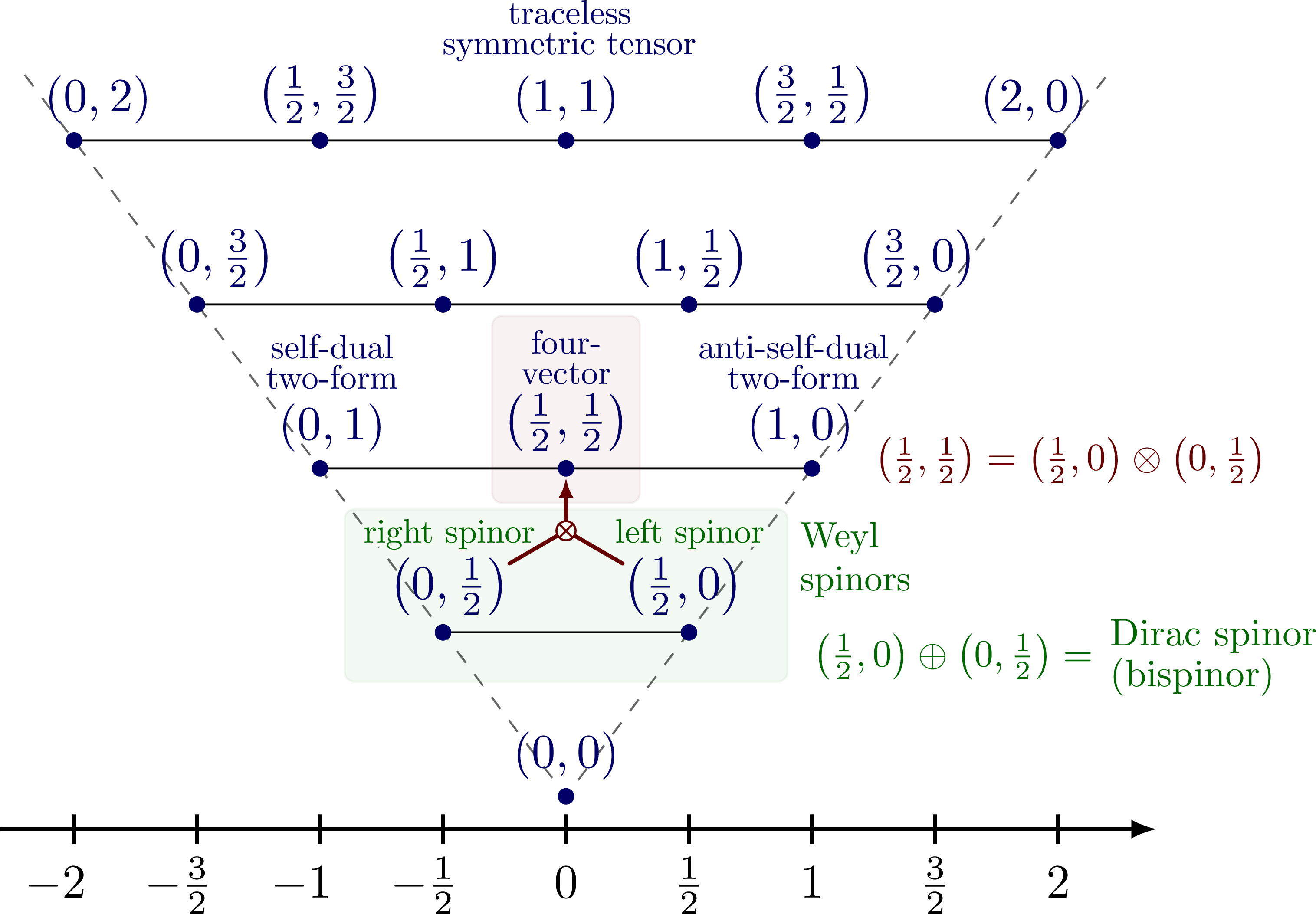
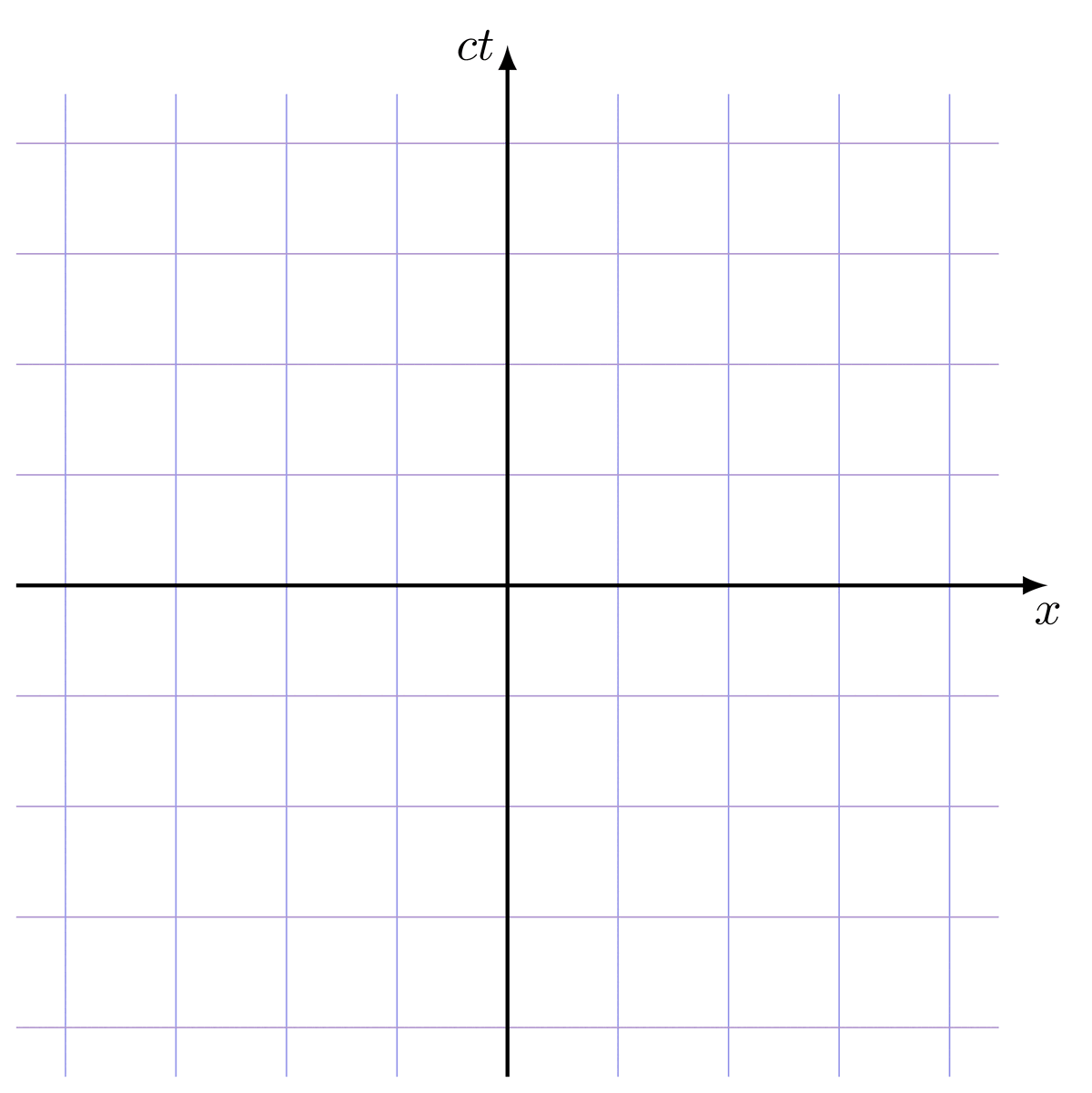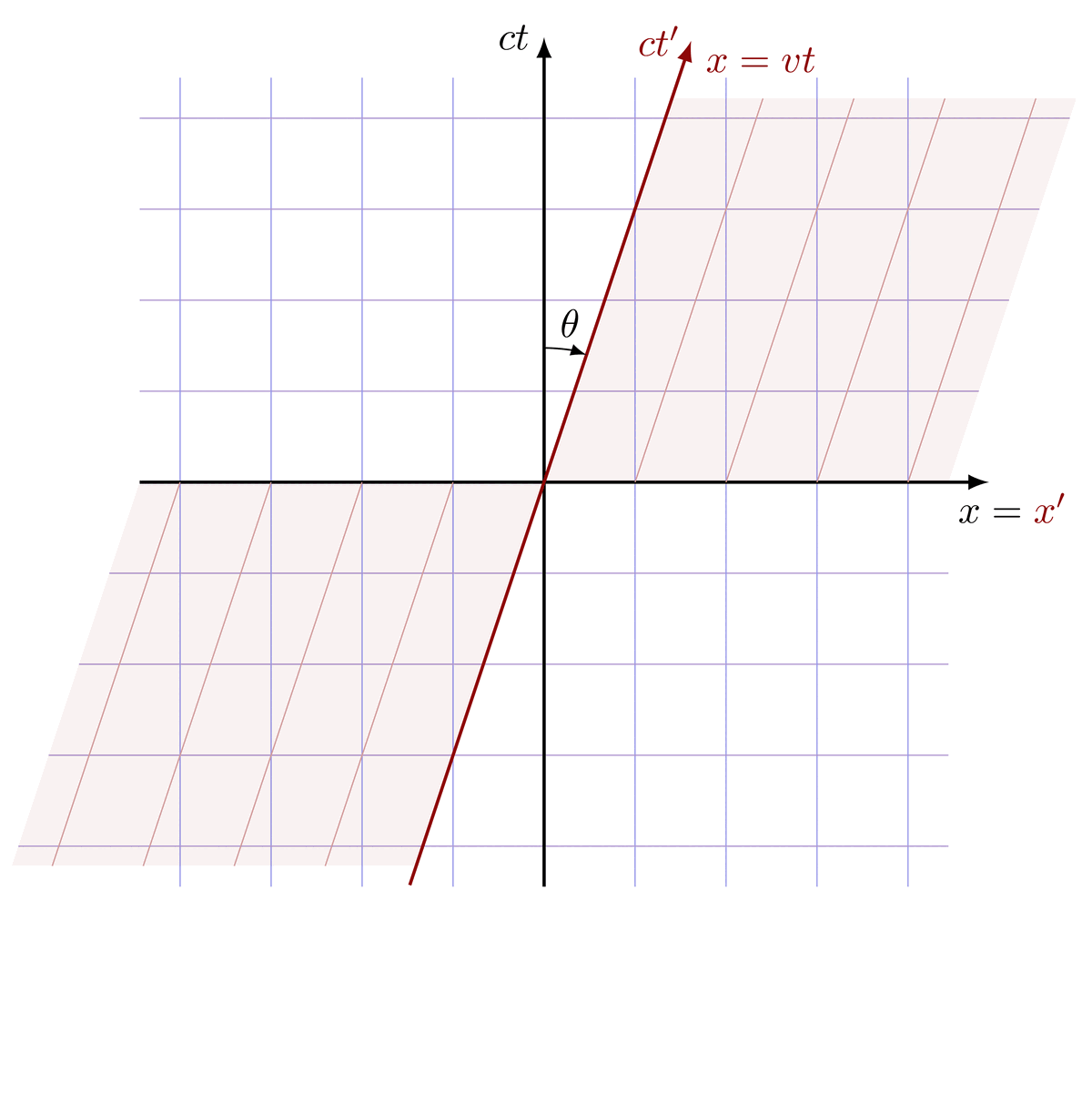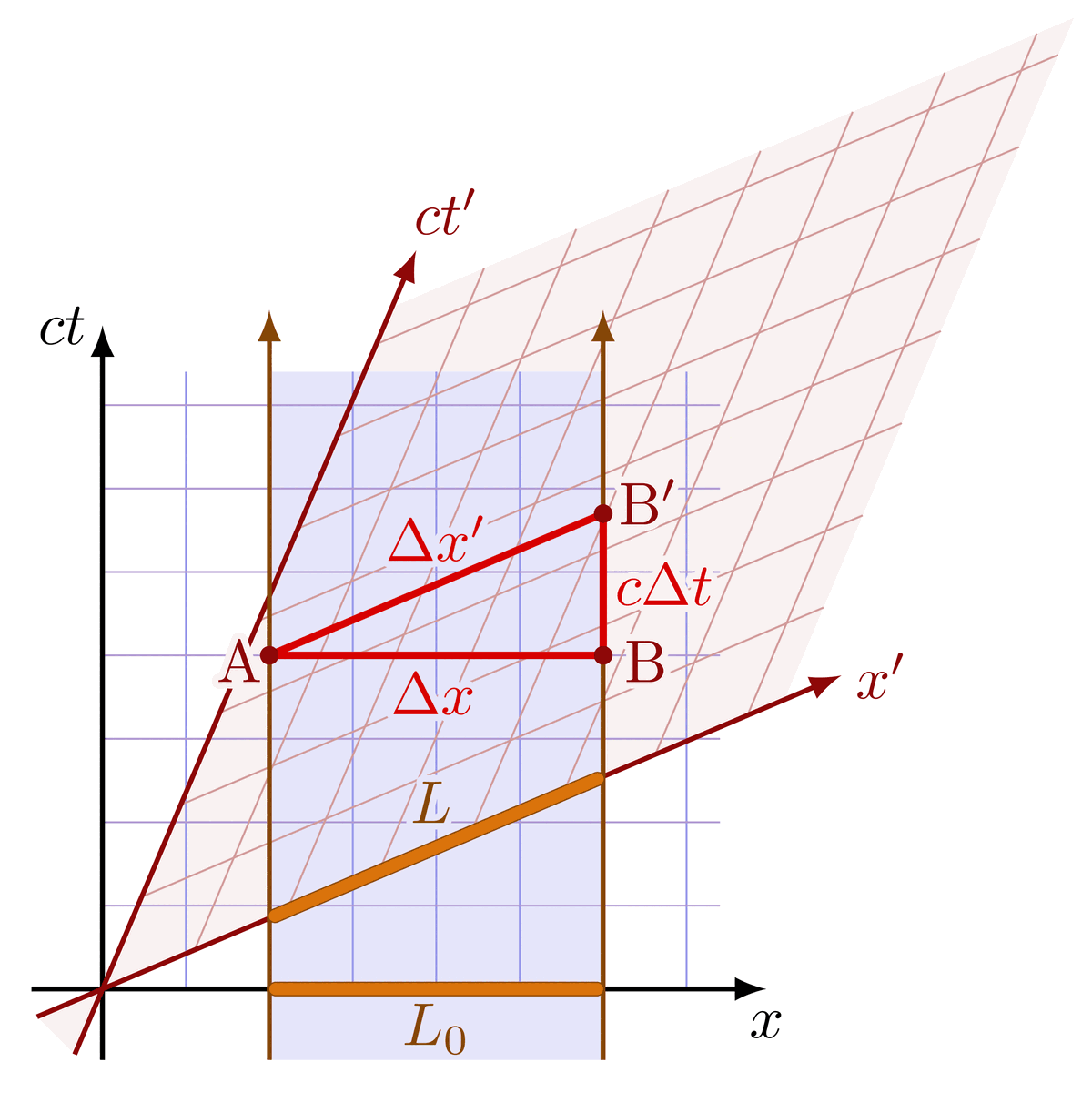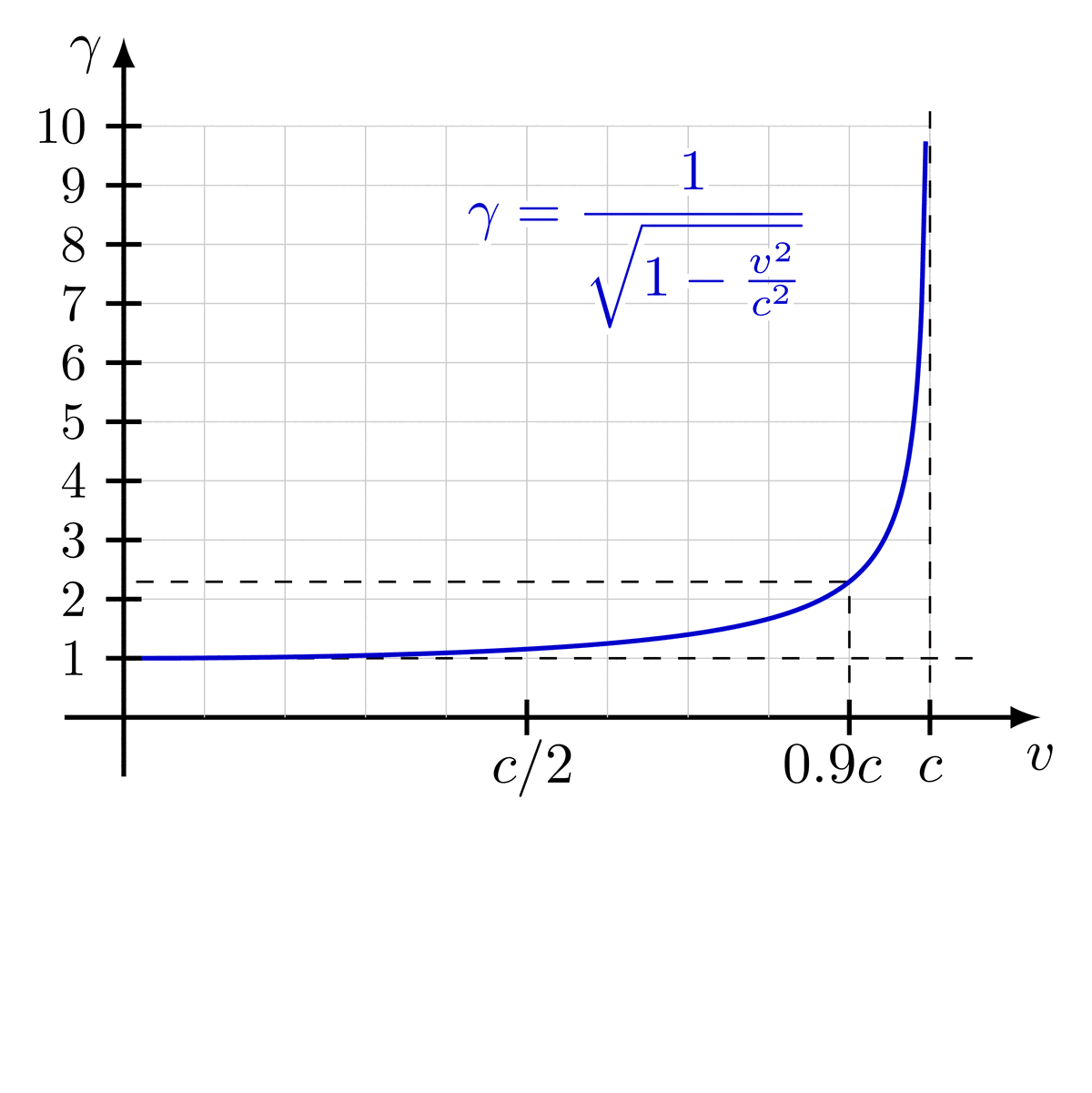
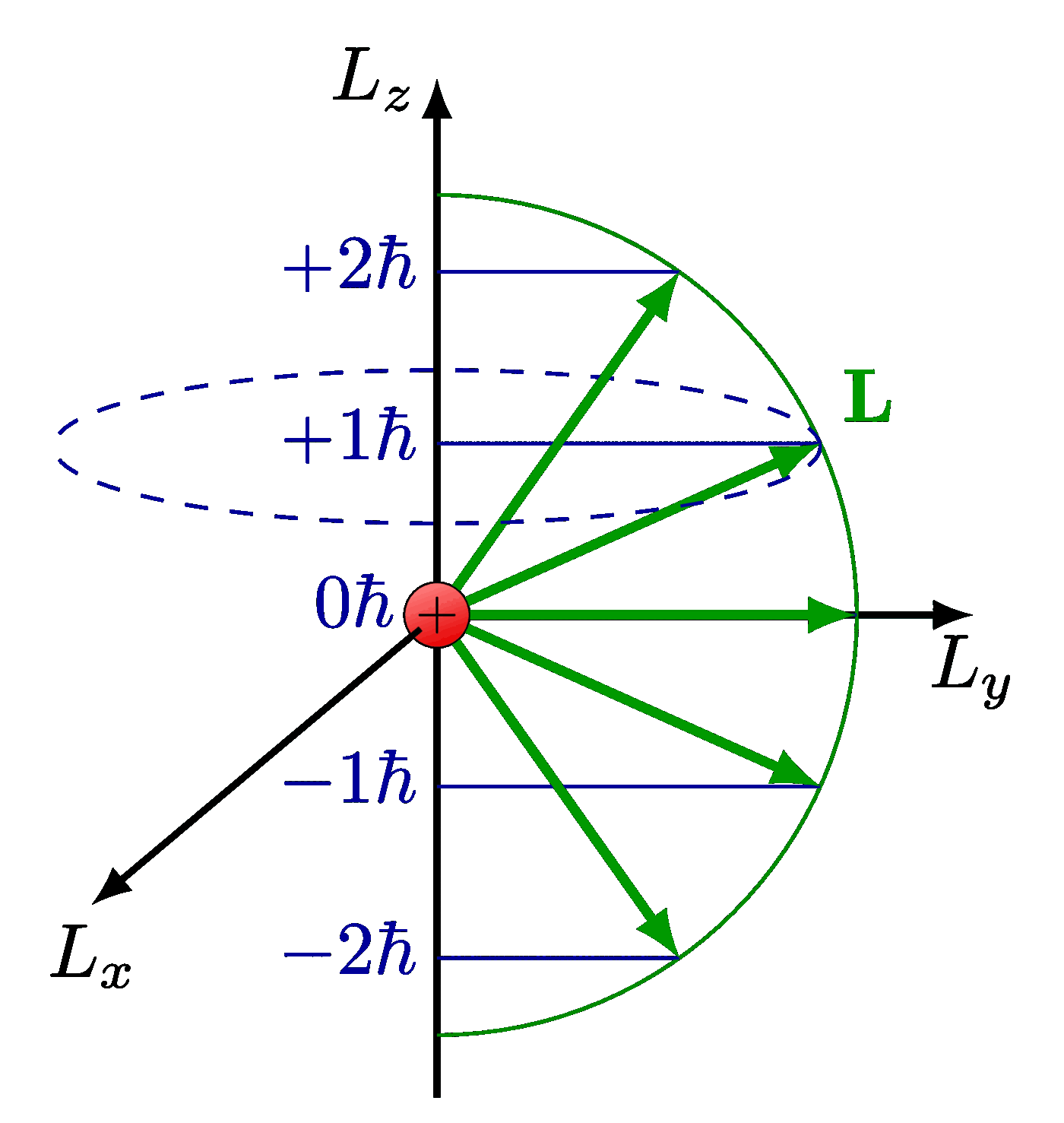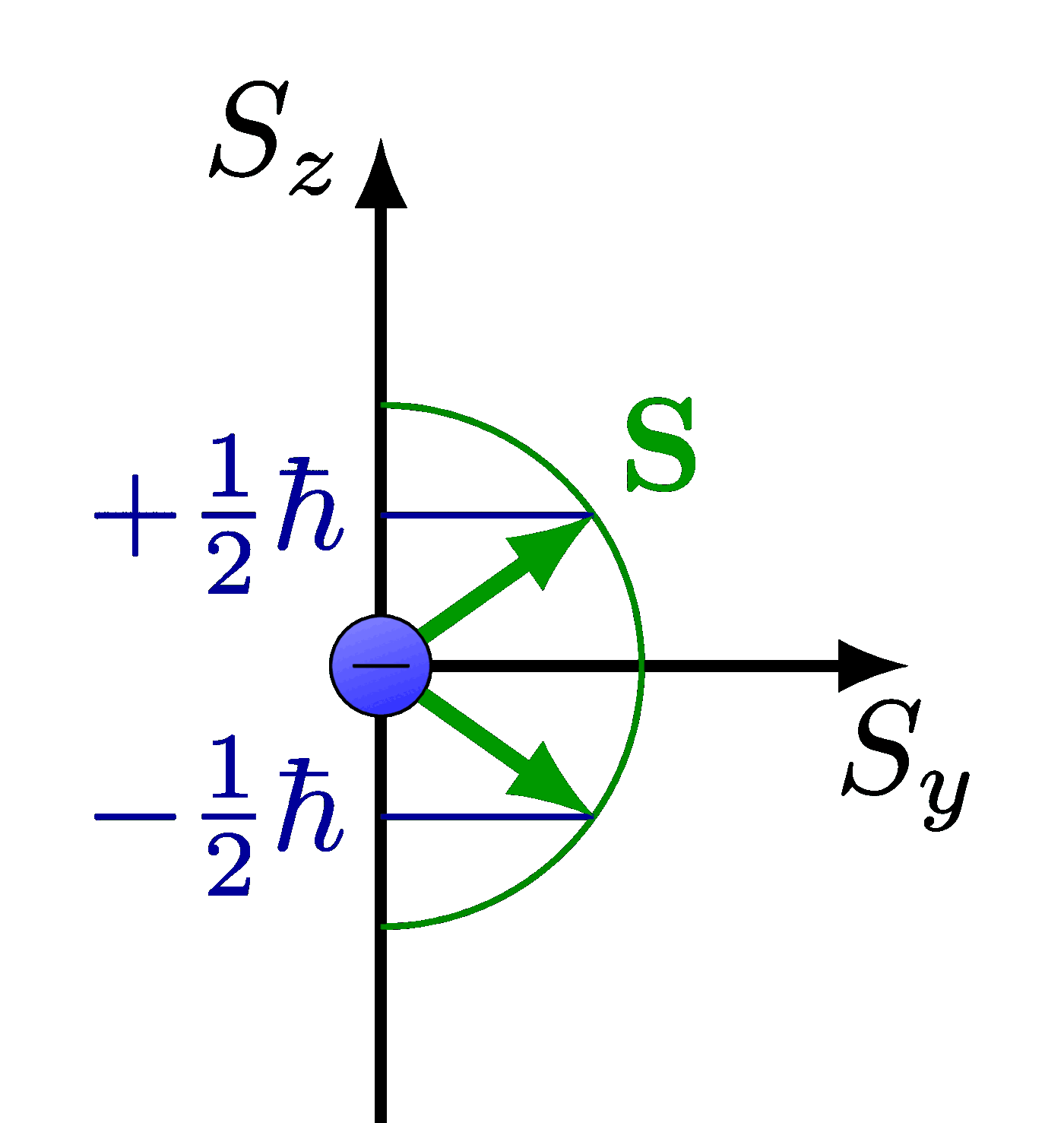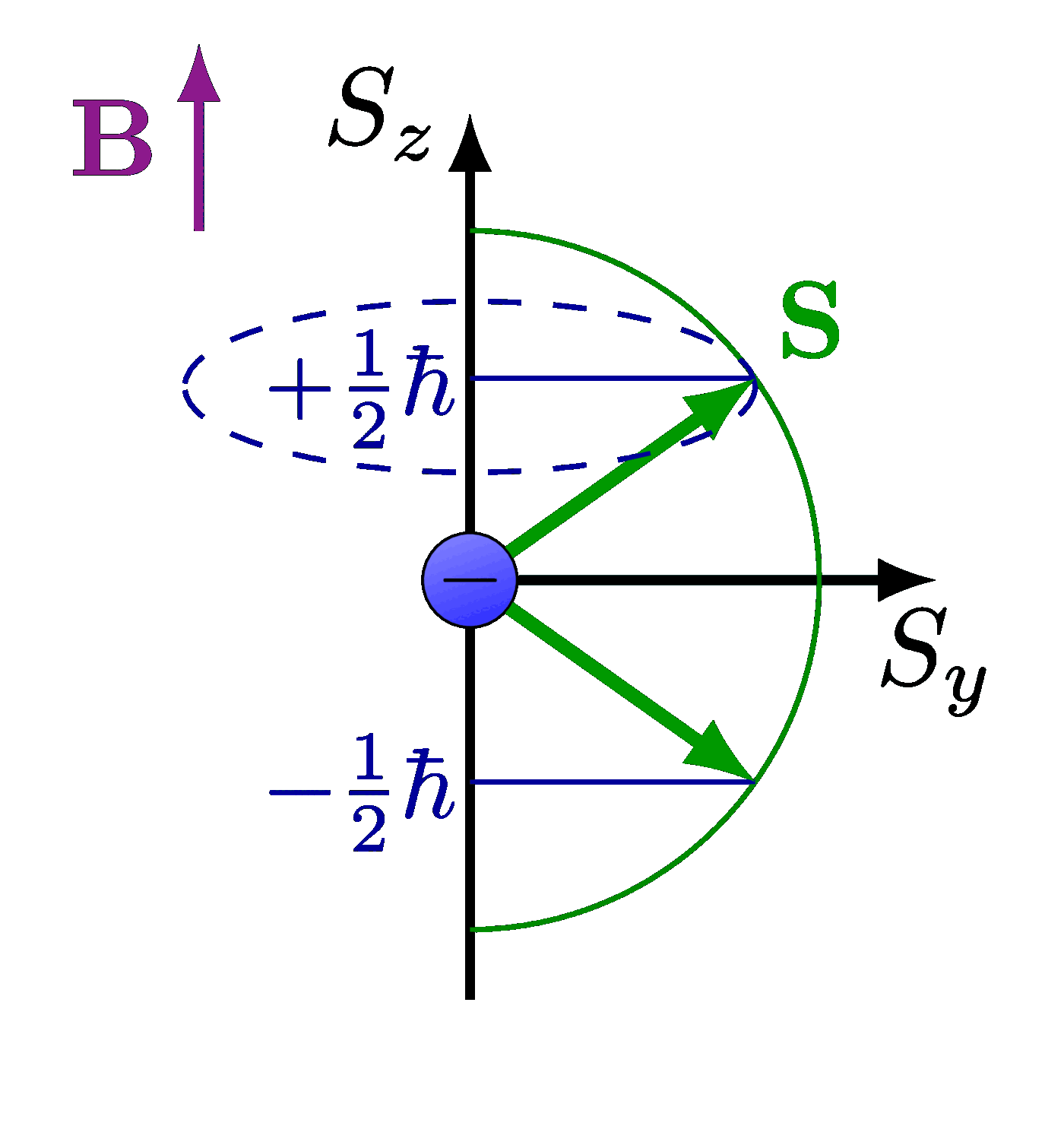
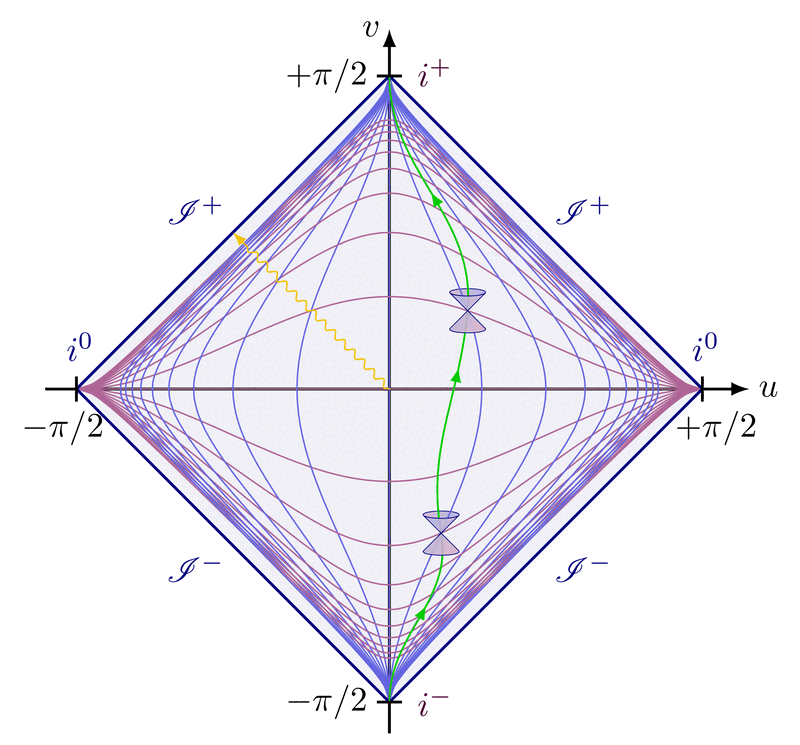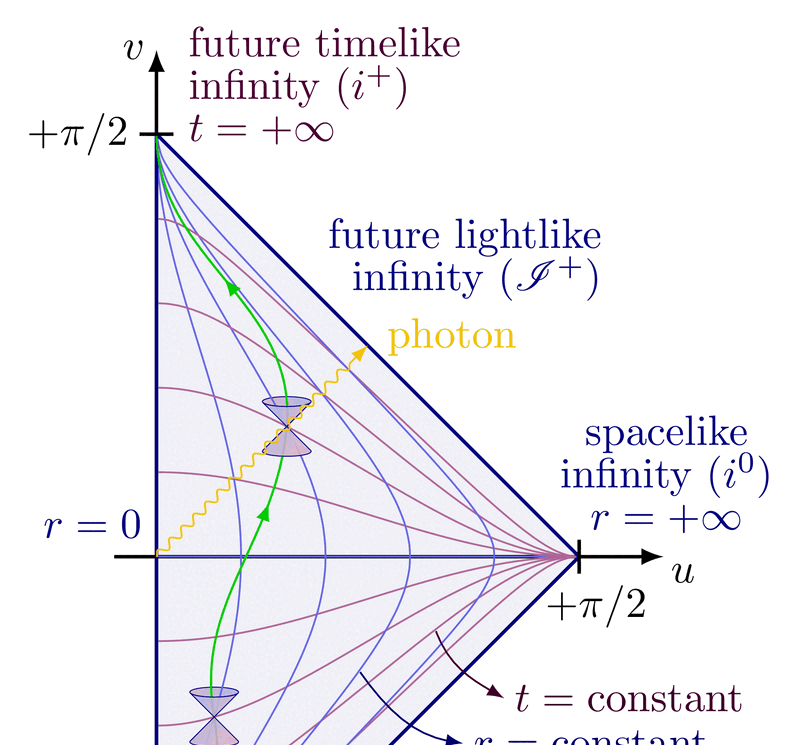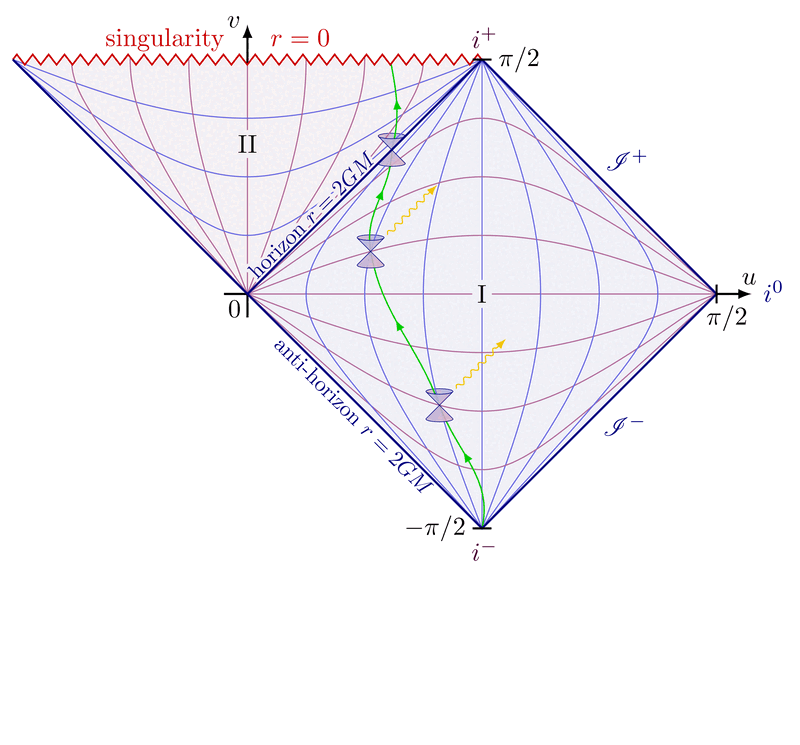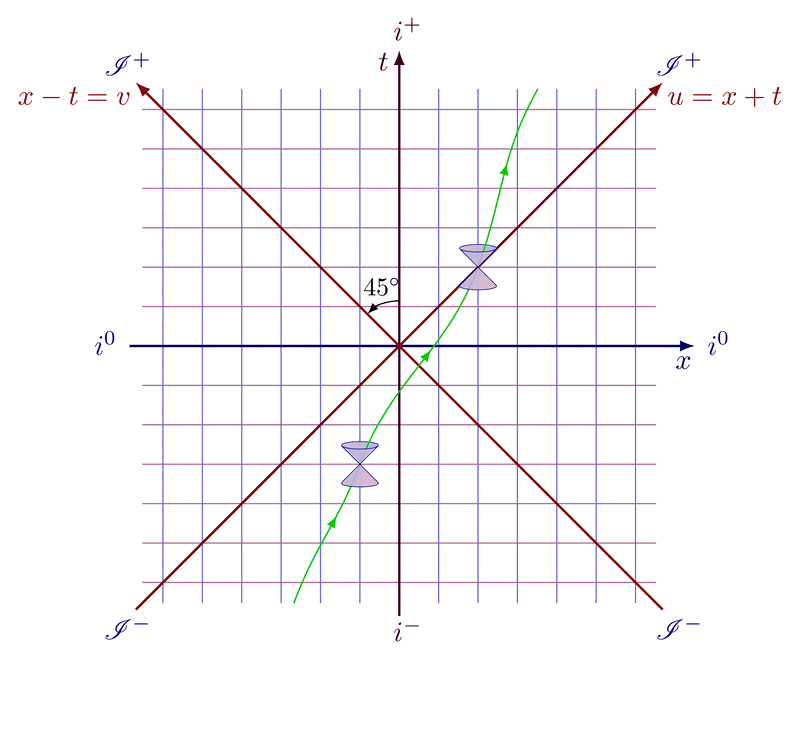
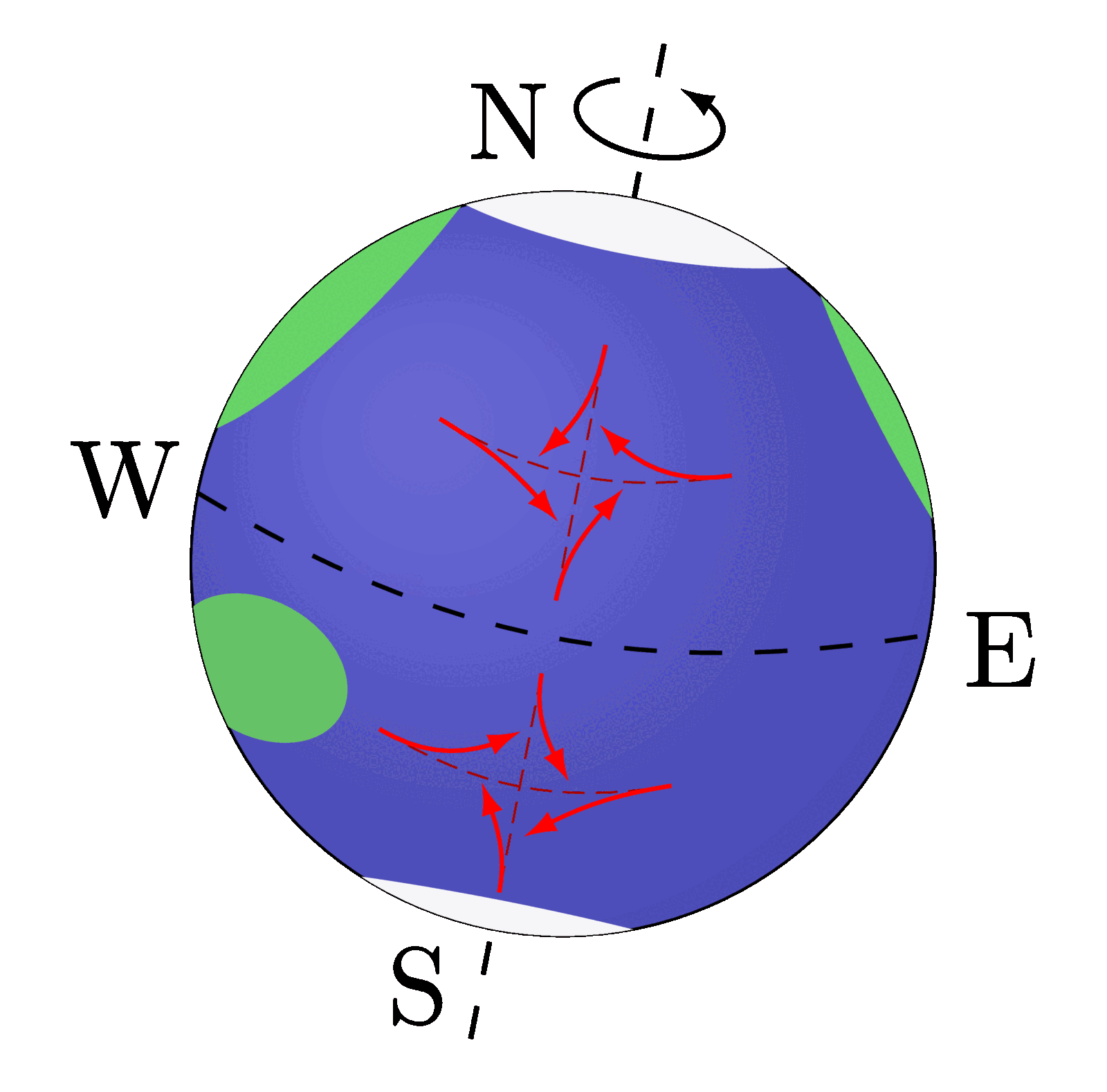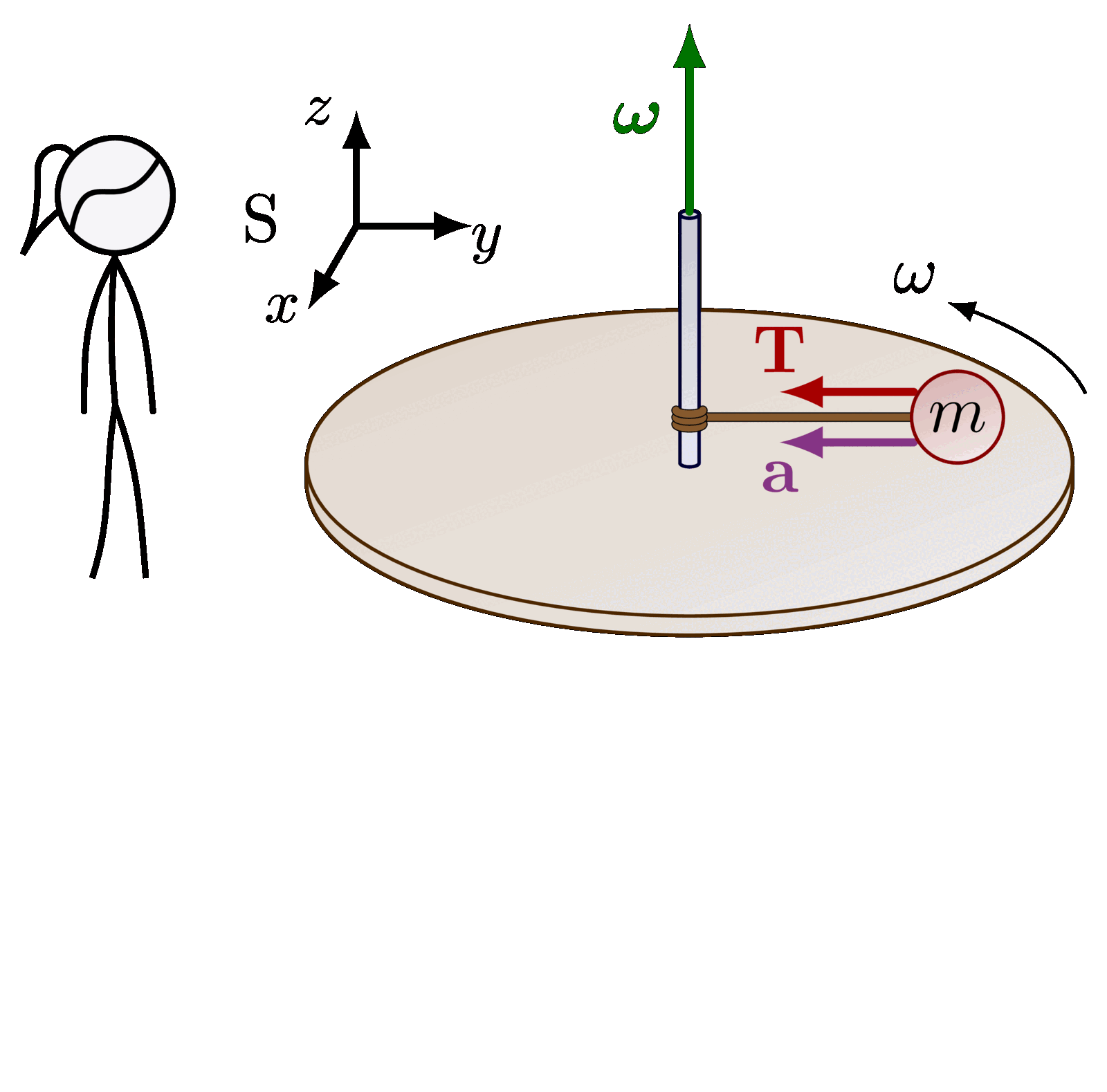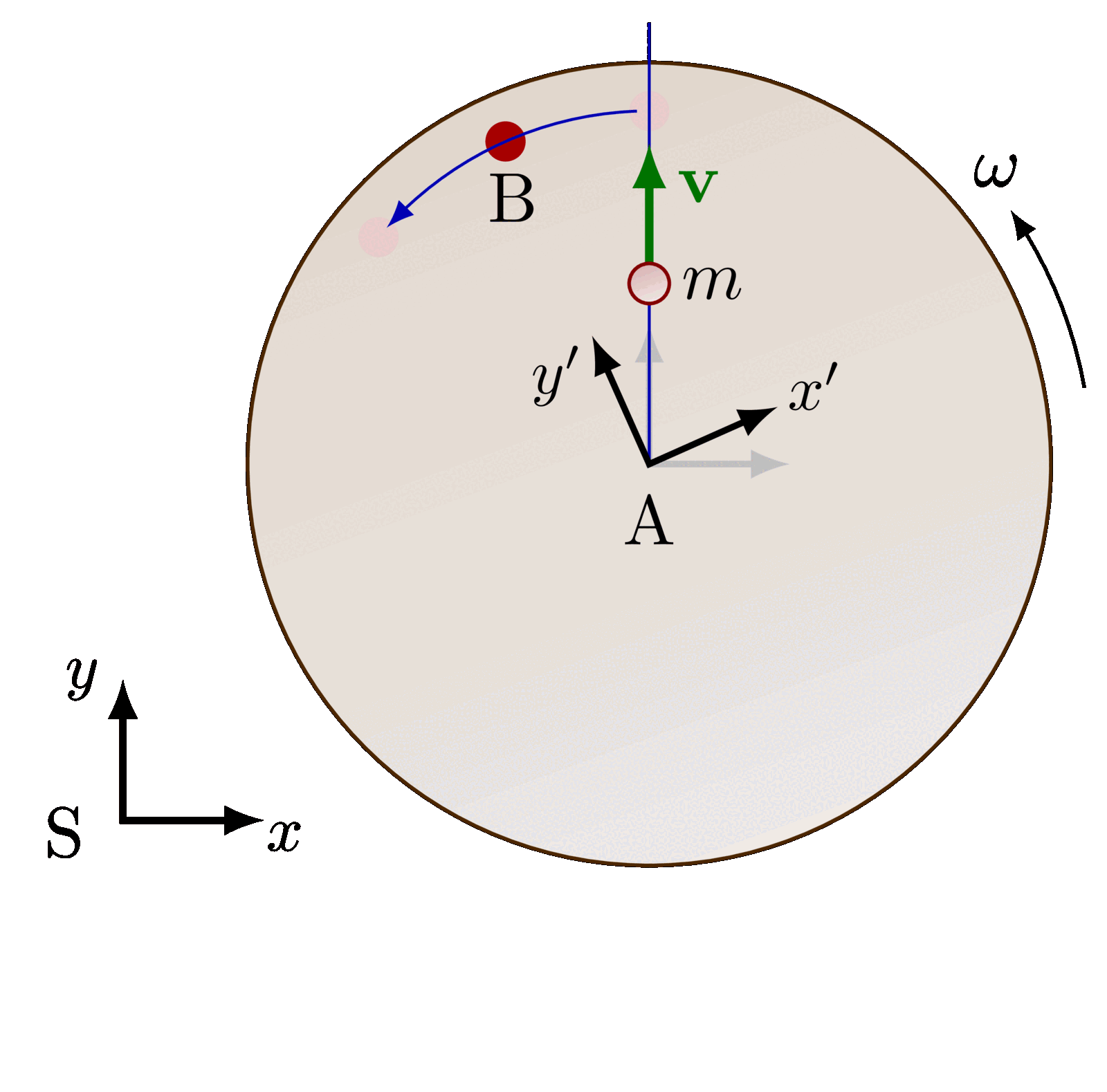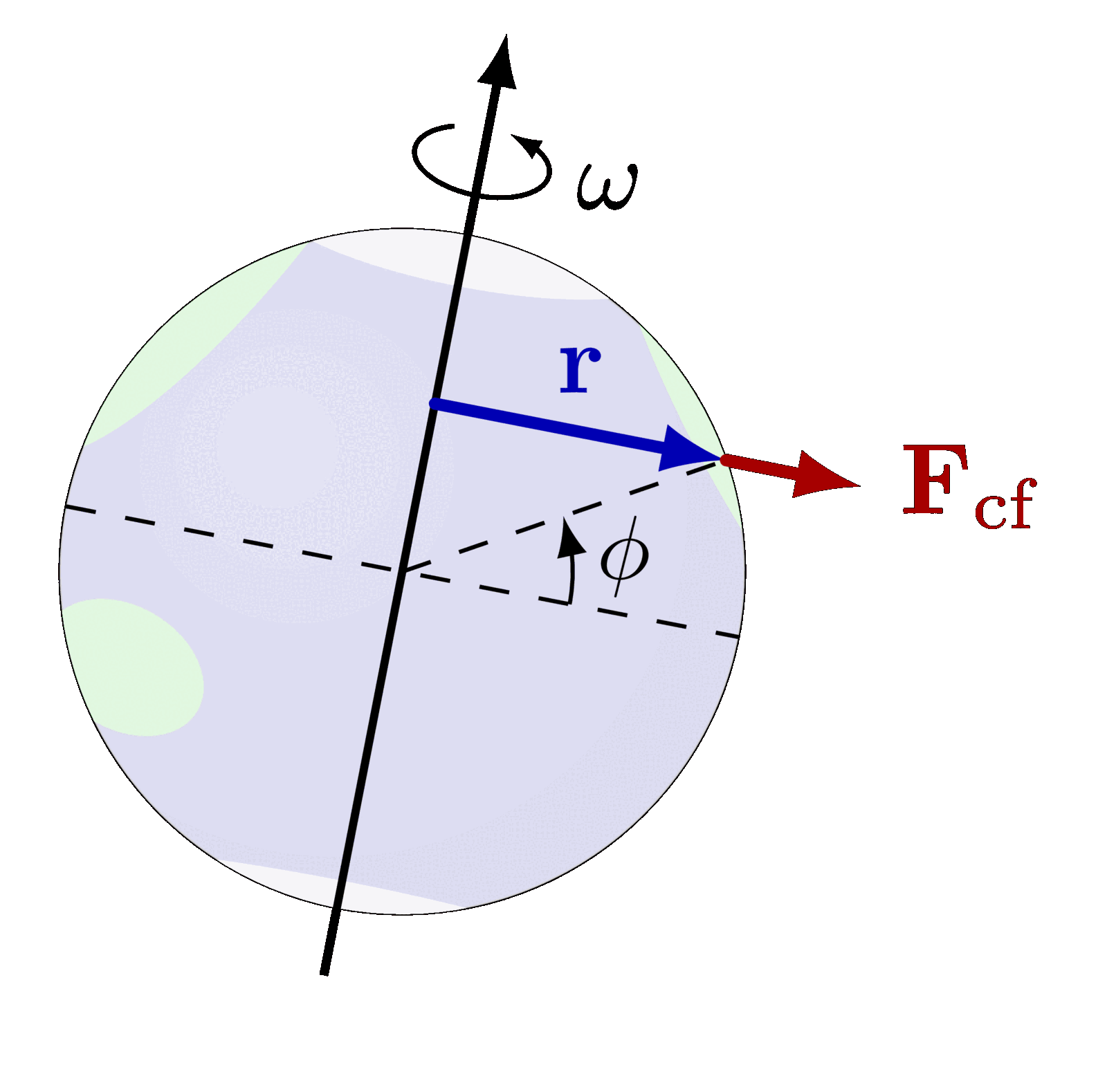
Lorentz group & representations

Lorentz group, Lorentz transformations and representations of the double cover. Inspired by Physics from Symmetry by Jakob Schwichtenberg, and Lorentz group and mass spectrum of elementary particles by Vadim V. Varlamov.

Edit and compile if you like:

% Author: Izaak Neutelings (August 2021)
% Sources & inspiration:
%  Physics from Symmetry (Jakob Schwichtenberg)
%  https://doi.org/10.3390/sym8090087 (Andreas Aste, https://www.mdpi.com/2073-8994/8/9/87/htm)
%  https://arxiv.org/abs/1705.02227 (V.V. Varlamov)
%  https://en.wikiversity.org/wiki/Representation_theory_of_the_Lorentz_group
\documentclass[border=2pt,tikz]{standalone}
\usepackage{tikz}
\usepackage{amsmath} % for \dfrac, \text, aligned
\usepackage{amssymb} % for \mathfrak
\usepackage{bbold} % for \mathbb
\usepackage[outline]{contour} % glow around text
\usetikzlibrary{arrows.meta} % to control arrow size
\usepackage{xcolor} % for colored text
\tikzset{>=latex} % for LaTeX arrow head
\contourlength{1.2pt}

\newcommand\LP{{\color{mydarkblue}P}} %\Lambda_\mathrm{P}
\newcommand\LT{{\color{mydarkred}T}} %\Lambda_\mathrm{T}
\colorlet{myred}{red!60!black}
\colorlet{myblue}{blue!60!black}
\colorlet{mygreen}{green!60!black}
\colorlet{mydarkblue}{blue!40!black}
\colorlet{mydarkred}{red!40!black}
\colorlet{mydarkgreen}{green!40!black}
\colorlet{mydarkpurple}{blue!50!red!50!black}
\tikzstyle{myarr}=[-{Latex[length=4,width=3]}]

\begin{document}


% LORENTZ TRANSFORMATIONS
\begin{tikzpicture}[scale=1.8]
  \def\is{1.0} % inner seperation of nodes
  
  % GROUPS
  \node[inner sep=\is,mydarkred] (Ld-) at (0,0) {$\mathcal{L}^\downarrow_-$};
  \node[inner sep=\is] (Lu+) at (0,1) {$\mathcal{L}^\uparrow_+$}; % SO+(1,3)
  \node[inner sep=\is,mydarkblue] (Lu-) at (1,1) {$\mathcal{L}^\uparrow_-$};
  \node[inner sep=\is,mydarkpurple] (Ld+) at (1,0) {$\mathcal{L}^\downarrow_+$};
  
  % ELEMENTS
  \node[anchor=-5,inner sep=10,scale=0.9] at (Lu+) {$\mathbb{1}\hspace{-.2em}\in$};
  \node[anchor= 5,inner sep=10,scale=0.9] at (Ld-) {$\LT\hspace{-.2em}\in$};
  \node[anchor=185,inner sep=10,scale=0.9] at (Lu-) {$\ni\hspace{-.2em}\LP$};
  \node[anchor=175,inner sep=10,scale=0.9] at (Ld+) {$\ni\hspace{-.2em}\color{mydarkpurple}-\mathbb{1}$};
  
  % ARROWS
  \draw[->,thick,mydarkred] (Lu+) -- (Ld-)
    node[midway,left=-1,scale=0.9] {$\LT$};
  \draw[->,thick,mydarkblue] (Lu+) -- (Lu-)
    node[midway,above=-1,scale=0.9] {$\LP$};
  \draw[->,thick,mydarkred] (Lu-) -- (Ld+)
    node[midway,right=-1,scale=0.9] {$\LT$};
  \draw[->,thick,mydarkblue] (Ld-) -- (Ld+)
    node[midway,below=-1,scale=0.9] {$\LP$};
  \draw[->,thick,mydarkpurple] (Lu+) -- (Ld+)
    node[pos=0.3,above right=-1,scale=0.9,rotate=-45]
      {$\LP\LT$};
  
\end{tikzpicture}


% LORENTZ TRANSFORMATIONS
\begin{tikzpicture}[xscale=2.5,yscale=1.5]
  \def\is{2.0} % inner seperation of nodes
  
  % GROUPS
  \node[inner sep=\is] (so) at (0,0) {$\mathfrak{so}(3;1)$};
  \node[inner sep=\is] (SO) at (0,1) {$\mathrm{SO}(3;1)^+$};
  \node[inner sep=\is] (GL) at (1,1) {$\mathrm{GL}(V)$};
  \node[inner sep=\is] (gl) at (1,0) {$\mathfrak{gl}(V)$};
  
  % ARROWS
  \draw[->,thick] (so) -- (SO) node[pos=0.45,left=-1,scale=0.9] {$\exp$};
  \draw[->,thick] (gl) -- (GL) node[pos=0.45,right=-1,scale=0.9] {$\exp$};
  \draw[->,thick] (SO) -- (GL) node[pos=0.45,above=-1,scale=0.9] {$\Pi$};
  \draw[->,thick] (so) -- (gl) node[pos=0.45,below=-1,scale=0.9] {$\pi$};
  
\end{tikzpicture}


% LORENTZ GROUP (DOUBLE COVER) REPRESENTATIONS
% Inspired by https://arxiv.org/abs/1705.02227 (V.V. Varlamov)
% https://en.wikiversity.org/wiki/Representation_theory_of_the_Lorentz_group#Common_representations
\begin{tikzpicture}[x=1.8cm,y=1.2cm]
  \def\N{4}      % number of spin states
  \def\r{0.07cm} % radius otimes
  \def\repr#1{   % format simple fraction
    \pgfmathsetmacro{\double}{int(2*#1)}
    \pgfmathsetmacro{\sign}{ifthenelse(#1<0,"-","")}
    \pgfmathparse{int(mod(\double,2))}
    \ifnum0=\pgfmathresult\relax % even
      \pgfmathprintnumber{#1}
    \else % odd
      \sign % sign
      \pgfmathparse{abs(int(\double))}
      \frac{\pgfmathprintnumber{\pgfmathresult}}{2}
    \fi
    \phantom{\sign} % for centered alignment
  }
  
  % AXIS
  \begin{scope}[shift={(0,-0.2)}]
    \draw[->,thick] (-\N/2-0.3,0) -- (\N/2+0.4,0); %node[right=-1] {$S$};
    \foreach \j [evaluate={\x=\j/2; \m=\j/2;}] in {-\N,...,\N}{ % ticks
      \draw[thick] (\x,0.09) --++ (0,-0.18)
        node[below=-1] {\strut$\repr{\m}$}; 
    }
  \end{scope}
  
  % LABELS Dirac spinor
  \draw[dashed,opacity=0.6] (-1.1*\N/2,1.1*\N) -- (0,0) -- (1.1*\N/2,1.1*\N);
  \draw[mydarkgreen,fill=mygreen,fill opacity=0.05,rounded corners=2]
    (-0.9,0.7) rectangle (0.9,1.75)
    node[mydarkgreen,below right,align=left,opacity=1,scale=0.75] {Weyl\\spinors};
  \node[mydarkgreen,scale=0.8,below right] at (0.95,1.2)
    {$\left(\frac{1}{2},0\right)\oplus\left(0,\frac{1}{2}\right)
       = \!\! \begin{array}{l}
           \text{Dirac spinor}\\[-0.5mm]
           \text{(bispinor)}
         \end{array}$};
  %\node[mydarkgreen,scale=0.8,below,align=center] at (1.55,0.68)
  %  {Dirac spinor\\[-3](bispinor)};
  %\node[mydarkgreen,scale=0.8,below,align=center] at (2.58,0.68)
  %  {four-\\[-3]vector};
  %\node[mydarkgreen,scale=0.8,below right] at (1.5,2.2)
  %  {$(1,0)\oplus(0,1) = \text{adjoint}$}; % parity-invariant 2-form field
  
  % LABELS four-vector
  \draw[mydarkred,fill=myred,fill opacity=0.05,rounded corners=2]
    (-0.3,1.79) rectangle (0.3,2.93);
  \node[mydarkred,scale=0.8,right] at (1.2,2.05)
    {$\left(\frac{1}{2},\frac{1}{2}\right) = %\cong
      \left(\frac{1}{2},0\right)\otimes\left(0,\frac{1}{2}\right)$};
  
  % DOTS
  \foreach \j [evaluate={\y=\j;}] in {0,...,\N}{
    \draw (-\j/2,\y) --++ (\j,0);
    \foreach \i [evaluate={
      \m=\i-\j/2;
      \L=\i/2; % left representation
      \R=\j/2-\i/2; % right representation
      \x=\m; % x position
      \myshift=((\i==0||\i==\j)?-2.5*\x:0);
    }] in {0,...,\j}{
      \fill[mydarkblue] (\x,\y) circle (0.06cm);
      \node[mydarkblue,right=\myshift,above]
        %,fill=white,text opacity=1,fill opacity=0.5,inner sep=0.5,outer sep=3
        (P\j-\i) at (\x,\y) {$\left(\repr{\L},\repr{\R}\right)$};
    }
  }
  
  % ARROWS & OTIMES
  \draw[thick,mydarkred,line cap=round]
    (-0.23,1.42) -- (0,1.62) coordinate (A) -- (0.23,1.42);
  \draw[myarr,thick,mydarkred,line cap=round]
    (A) -- (0,1.94);
  \draw[mydarkred,line width=0.4,fill=mygreen!5] % circle
    (A) circle(\r);
  \draw[mydarkred,line width=0.4] % cross
    (A)++(45:\r) --++ (-135:2*\r)
    (A)++(135:\r) --++ (-45:2*\r);
  
  % LABELS
  \node[mydarkgreen,scale=0.7,above=6]
    at (P1-0) {\strut\contour{mygreen!5}{right spinor}};
  \node[mydarkgreen,scale=0.7,right=2,above=6]
    at (P1-1) {\strut\contour{mygreen!5}{left spinor}};
  \node[mydarkblue,scale=0.7,above=8,align=center]
    at (P2-0) {self-dual\\[-3]two-form};
  \node[mydarkblue,scale=0.7,above=8,align=center]
    at (P2-1) {four-\\[-3]vector};
  \node[mydarkblue,scale=0.7,left=2,above=8,align=center]
    at (P2-2) {anti-self-dual\\[-3]two-form};
  \node[mydarkblue,scale=0.7,right=1,above=8,align=center]
    at (P4-2) {traceless\\[-3]symmetric tensor};
  
\end{tikzpicture}


\end{document}