This post contains Minkowski diagrams of flat spacetime with light cones to illustrate the causal structure, as well as graphical interpretations of Lorentz transformations (“boosts”), and more. Some figures were inspired by Very special relativity – An illustrated guide by Sander Bais. For more related figures made with TikZ, please see Relativity category. An excellent and animated explanation of Lorentz transformation is given by this YouTube video by ScienceClic English.
Table of content:
- World lines
- Causal structure of Minkowski spacetime
- Coordinate transformations
- Simultaneity
- Time dilation
- Length contraction
- Paradoxes
- Hyperbolae
- Analogy to Euclidean rotation
- Lorentz factor
- Full code
World lines
Empty spacetime diagram.
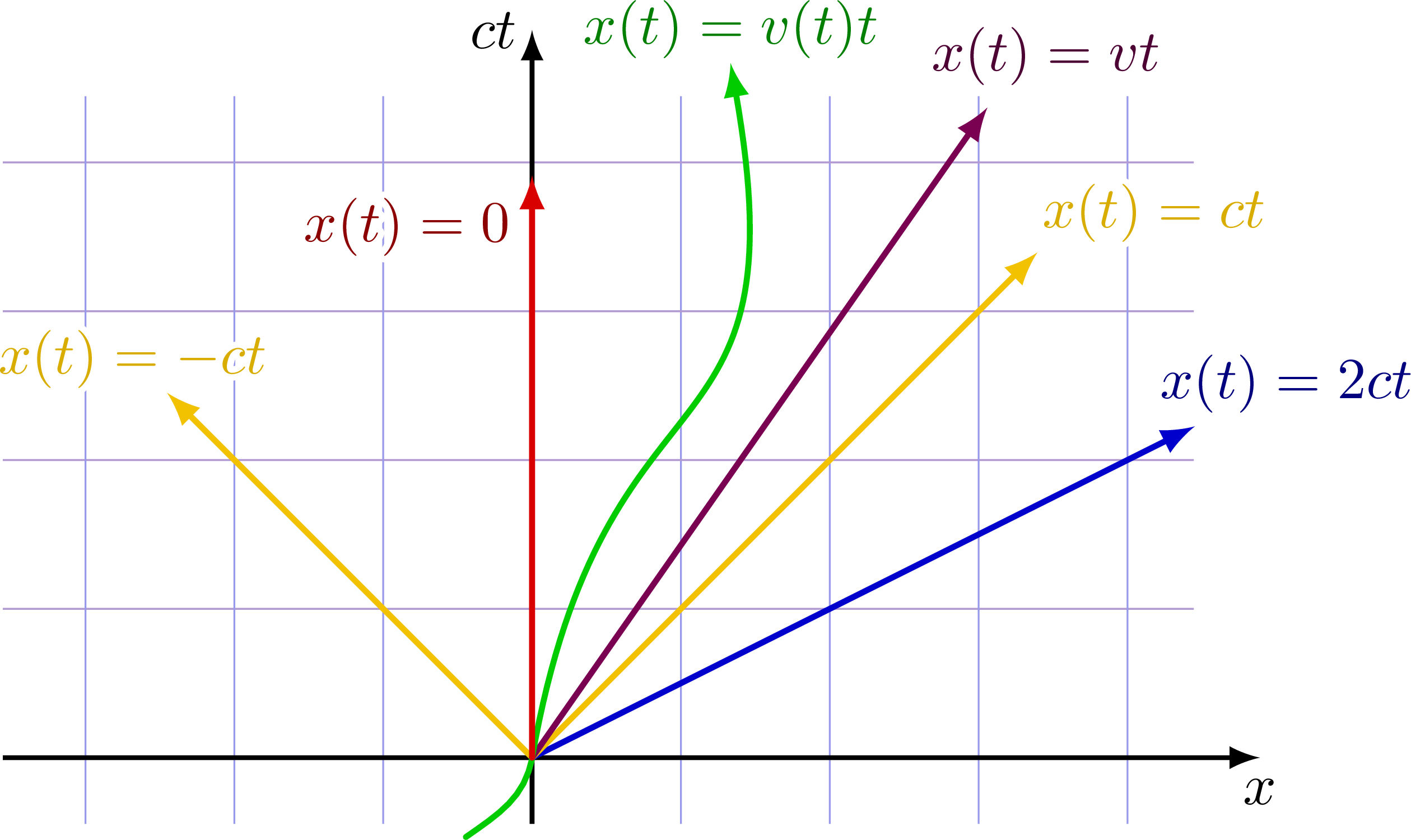
Several spacetime worldlines with different velocities.
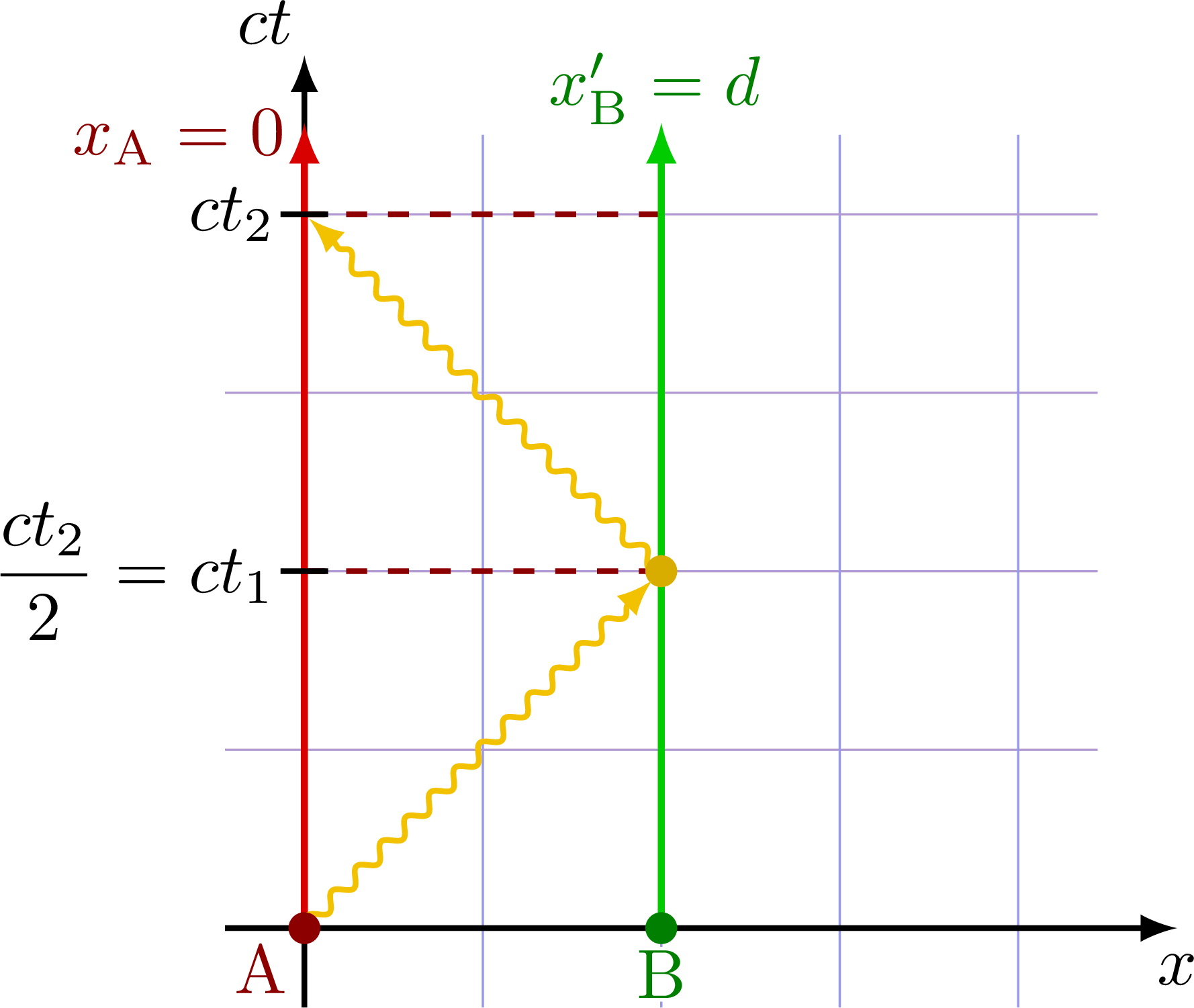
Two observers at rest (w.r.t. to each other) communicating by reflecting a light signal.
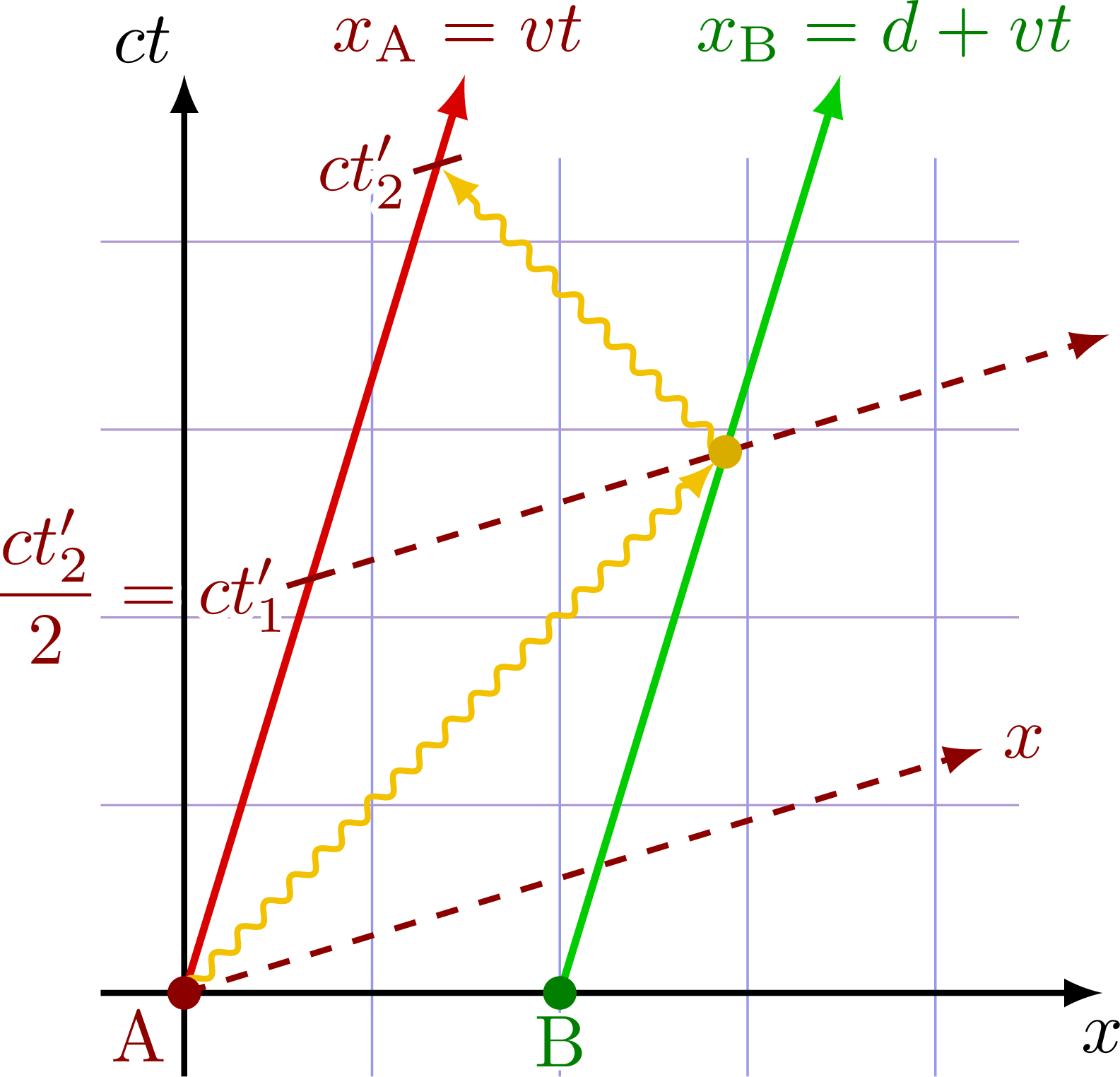
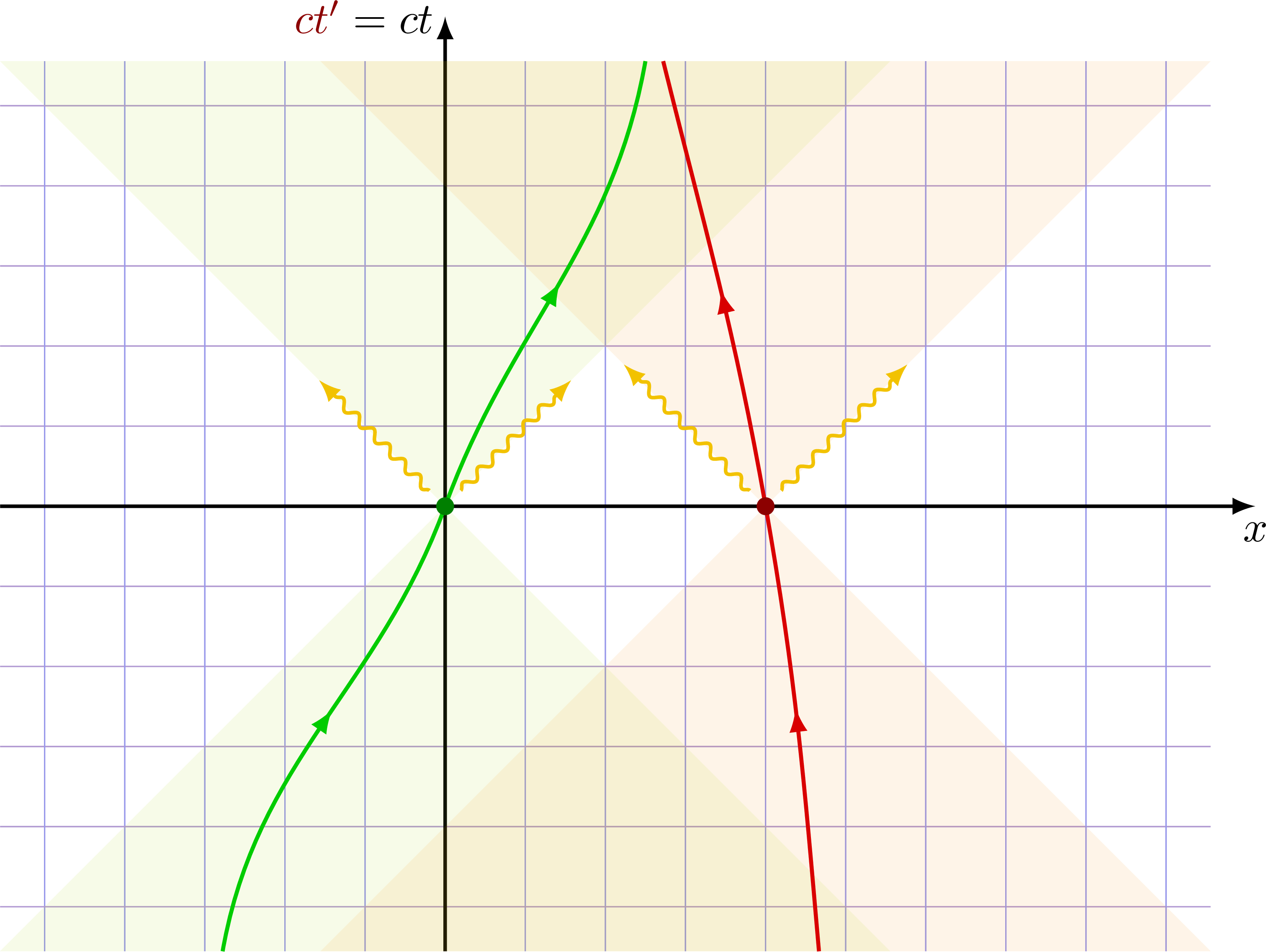
Derivation of the relativity of simultaneity with the thought experiment of two moving observers (with the red and green worldlines) communicating with a light signal. Assuming the speed of light is c in all inertial frame of references (second postulate of special relativity), the dashed lines represent the plane of simultaneity. All events on a given dashed line happen at the same time from the point of view of the moving observers.
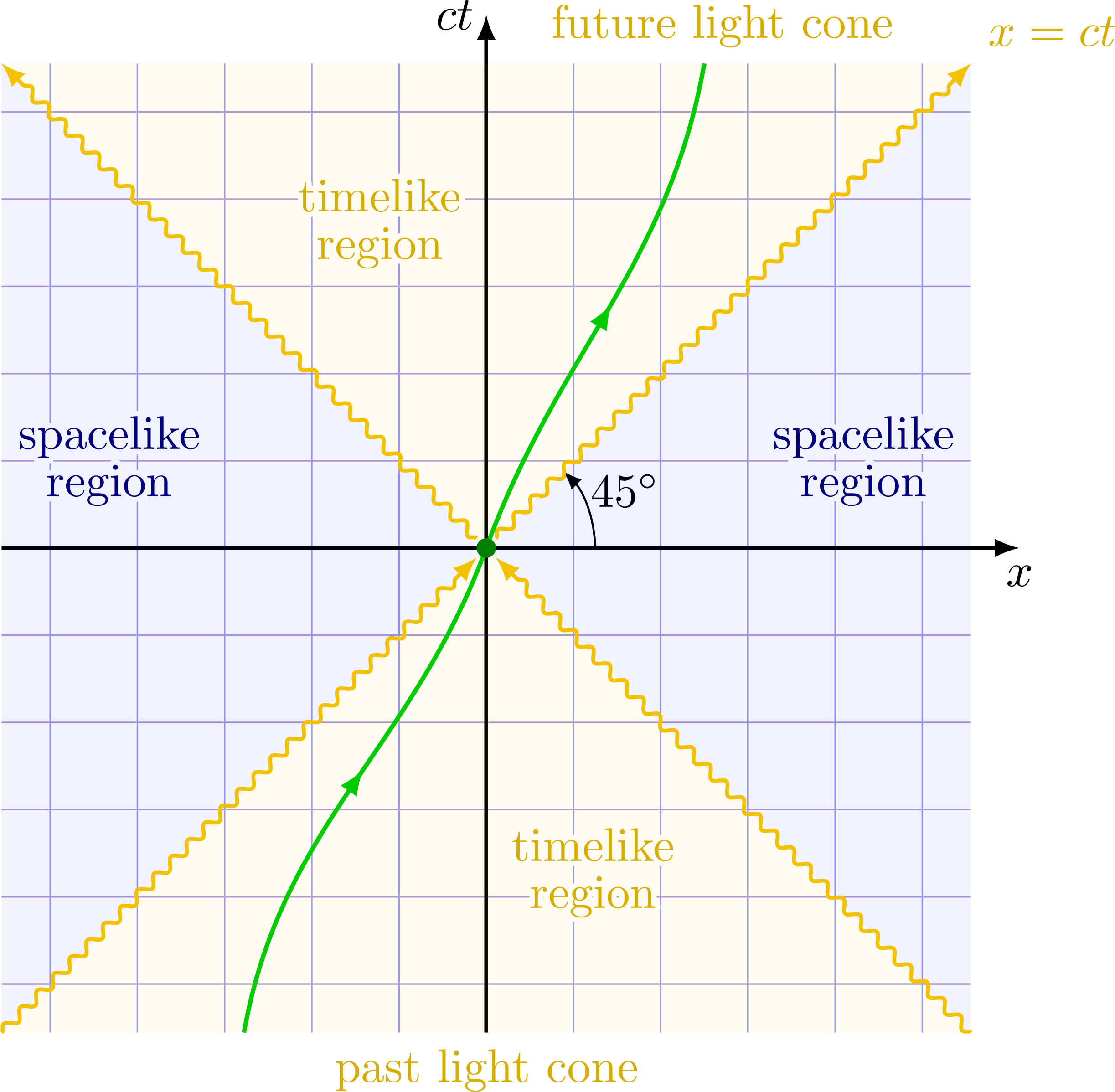
Causal structure of Minkowski spacetime
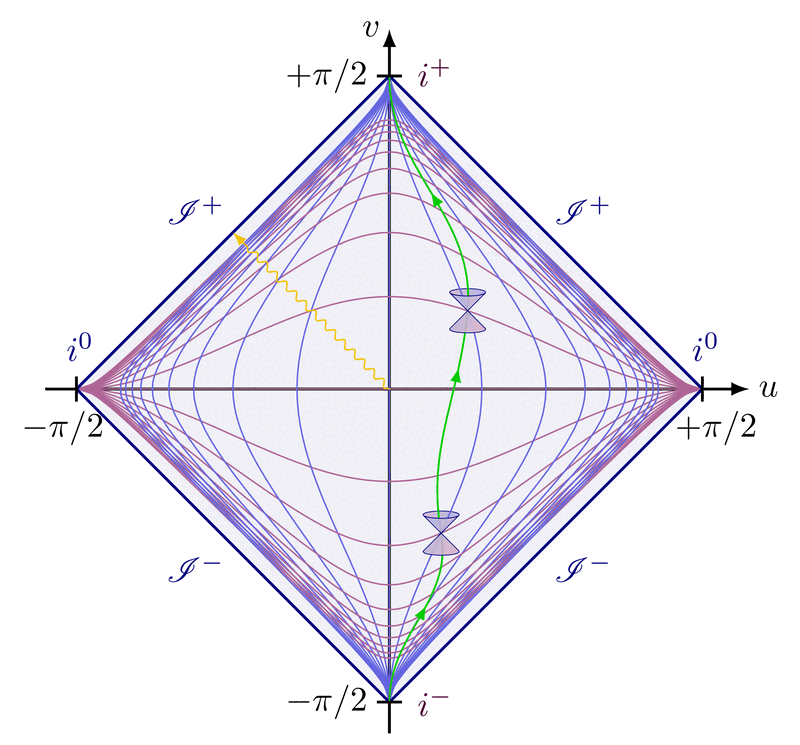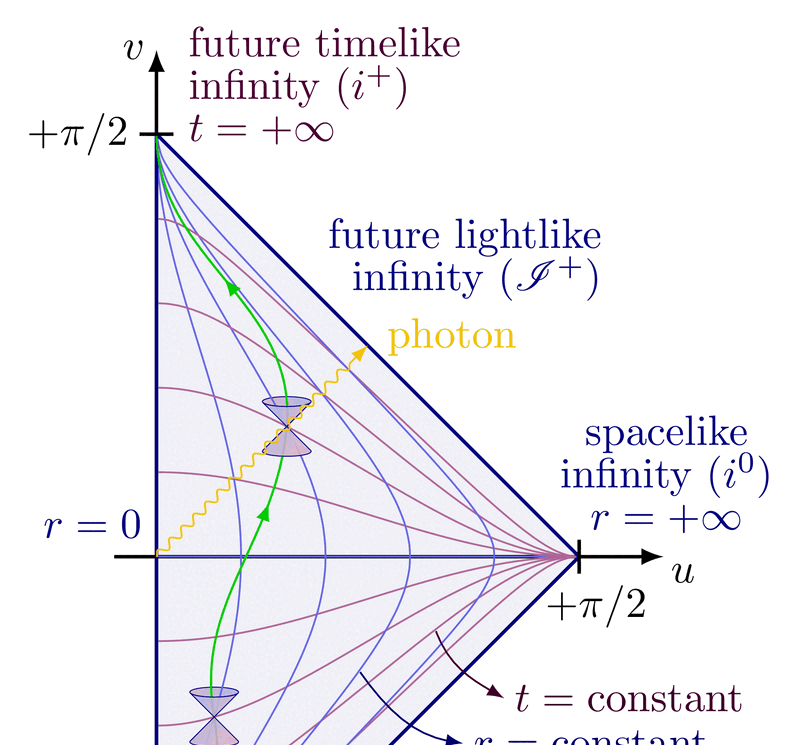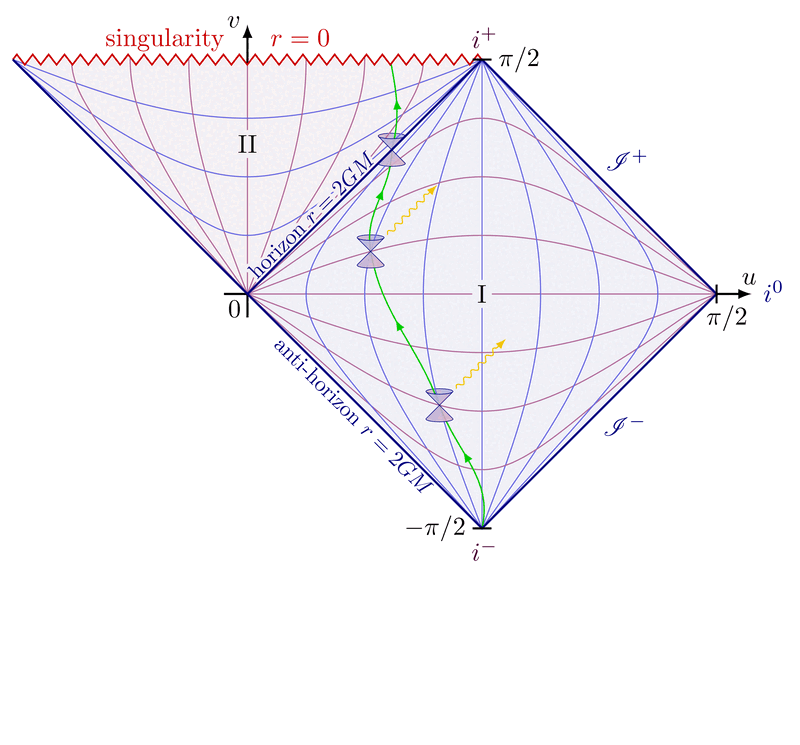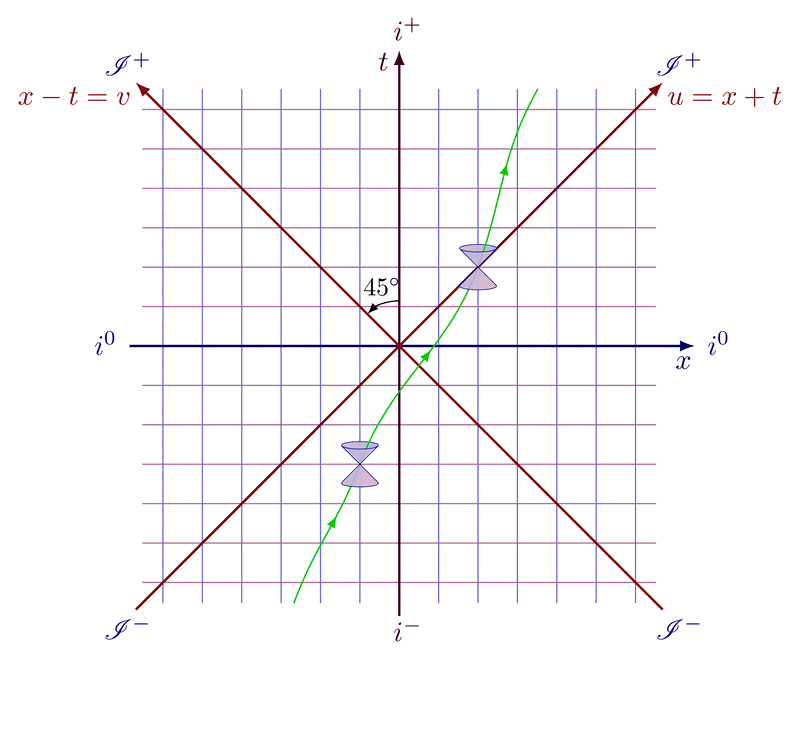
Future and past lightcone at a 45 degrees angle to illustrate the causal structure of Minkowski space.
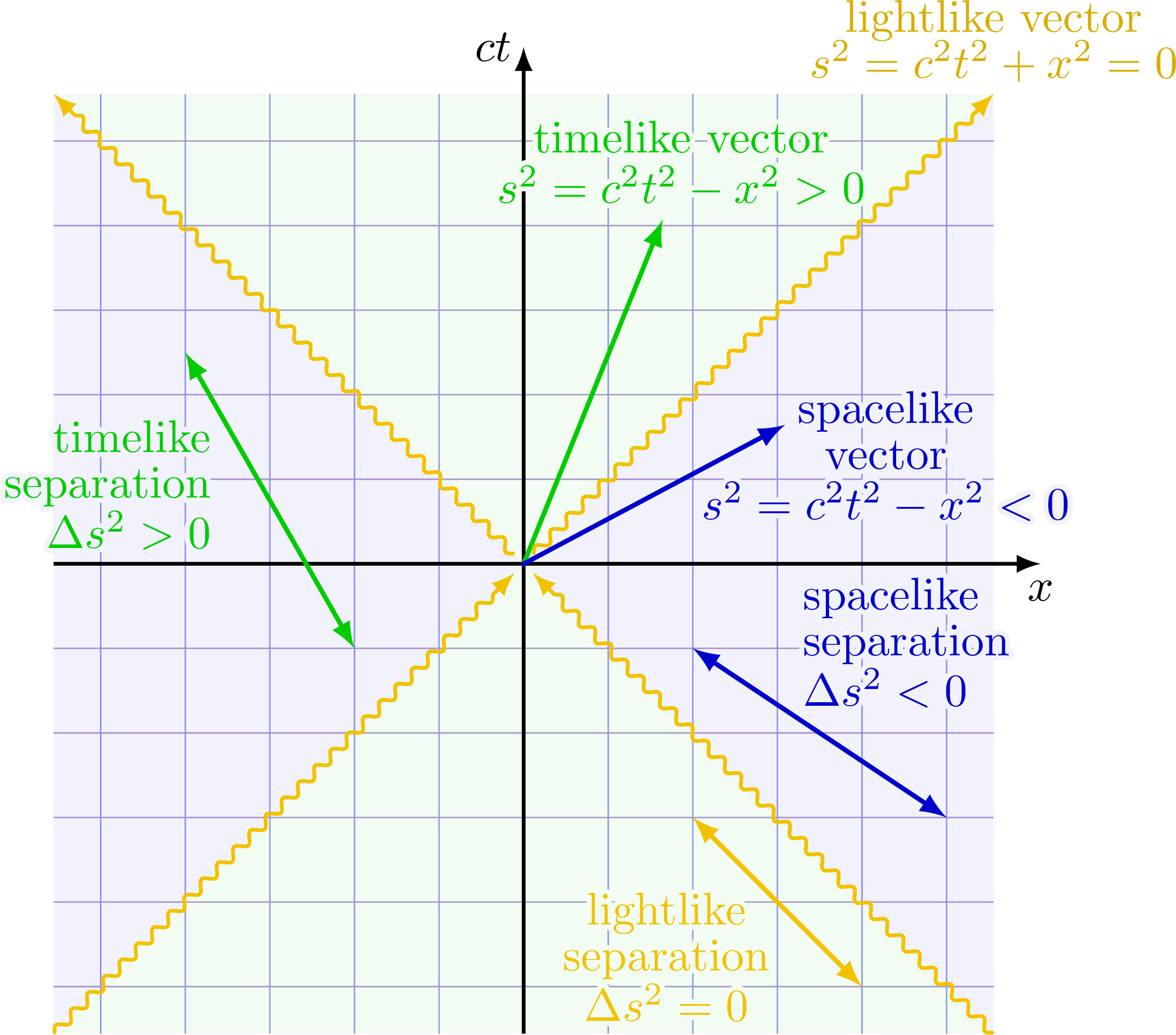
Different types of spacetime vectors and separation: timelike (s2 > 0), spacelike (s2 = 0) and lightlike or null (s2 < 0).
Overlapping light cones of two observers separated in spacetime to illustrate the causal structure.
Coordinate transformations
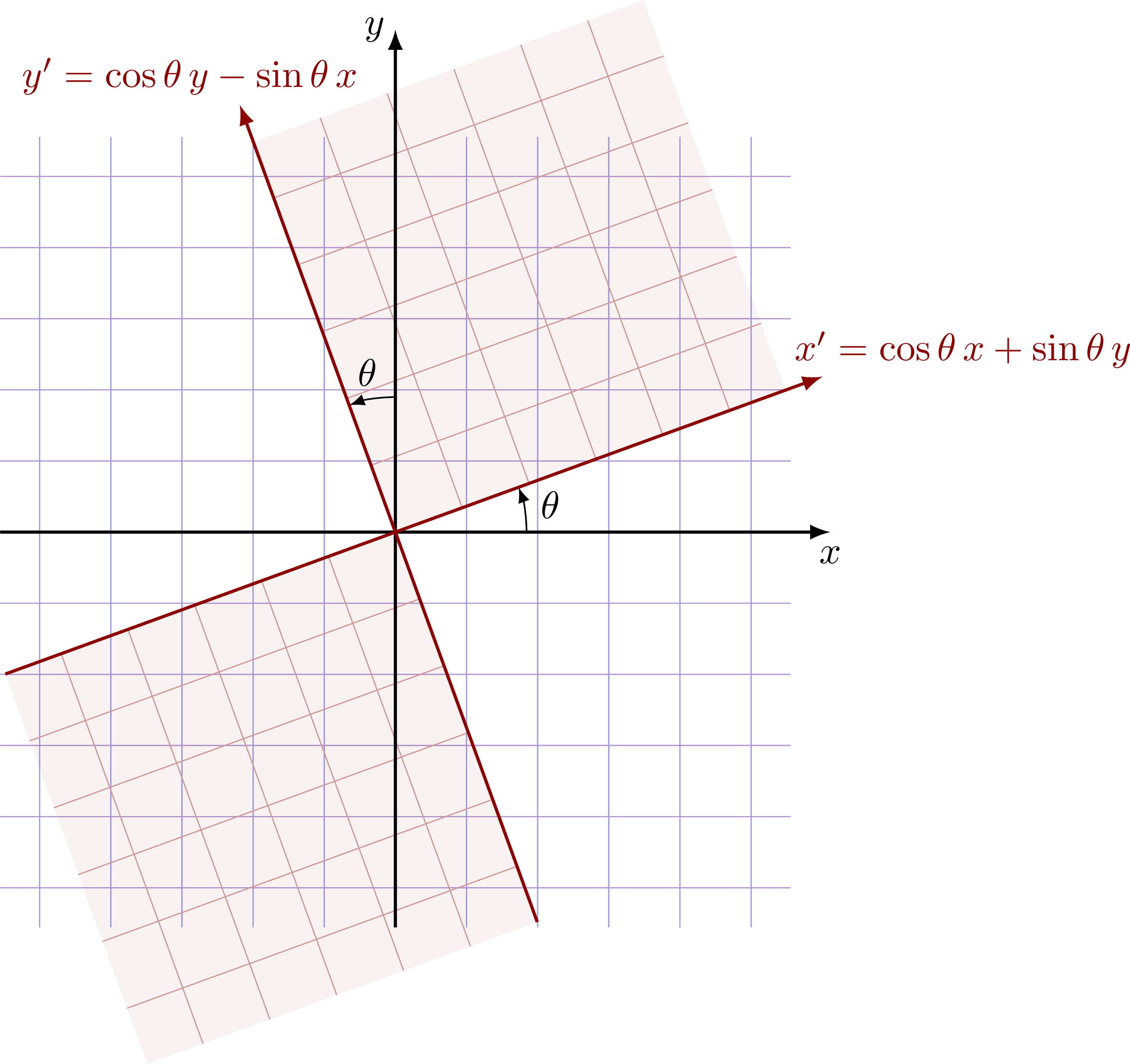
Simple 2D rotation in the (Euclidean) xy plane.
Galilean transformation for a moving frame. Clocks in both frames are equal (the grid lines at constant time ct and ct’ coincide).
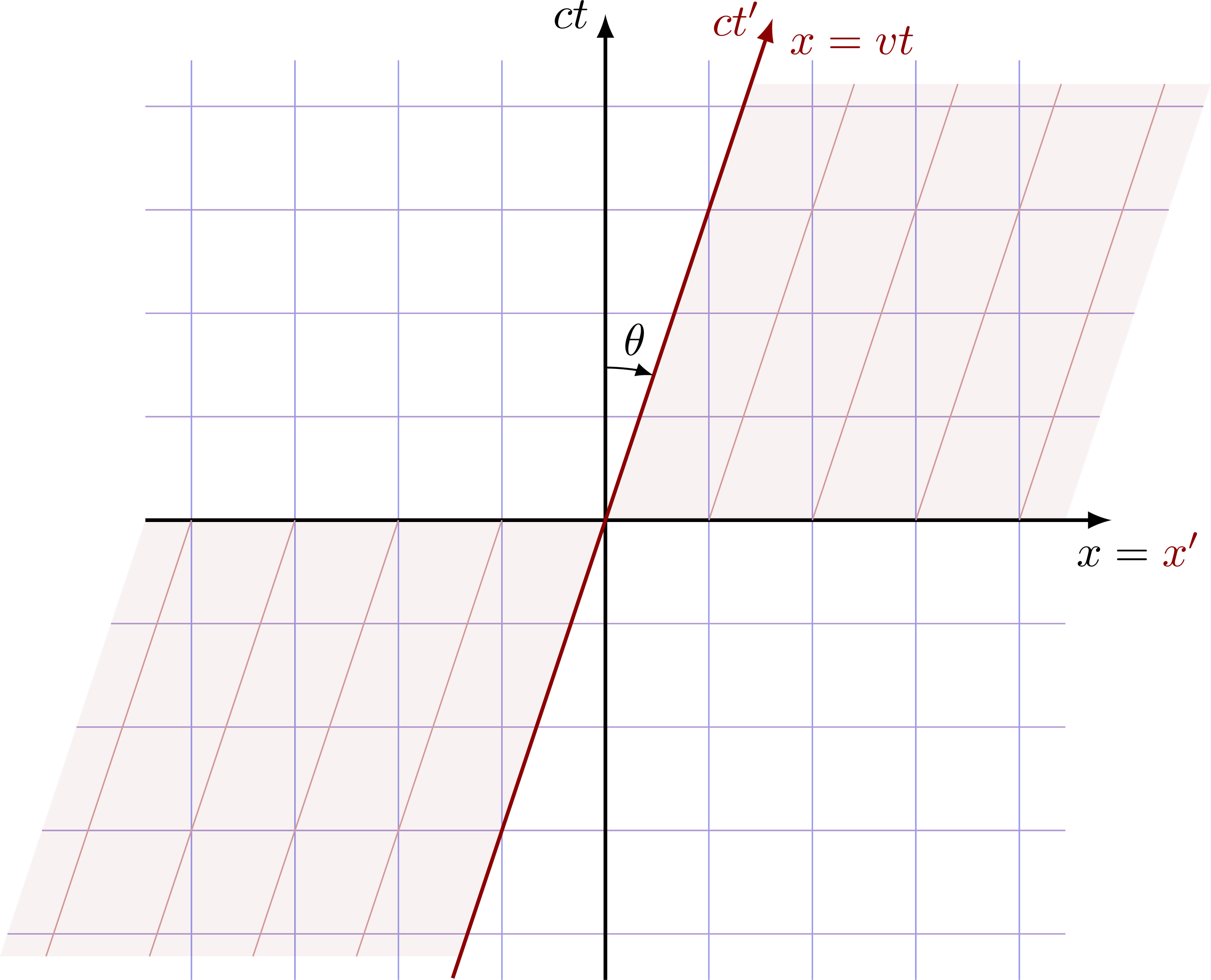
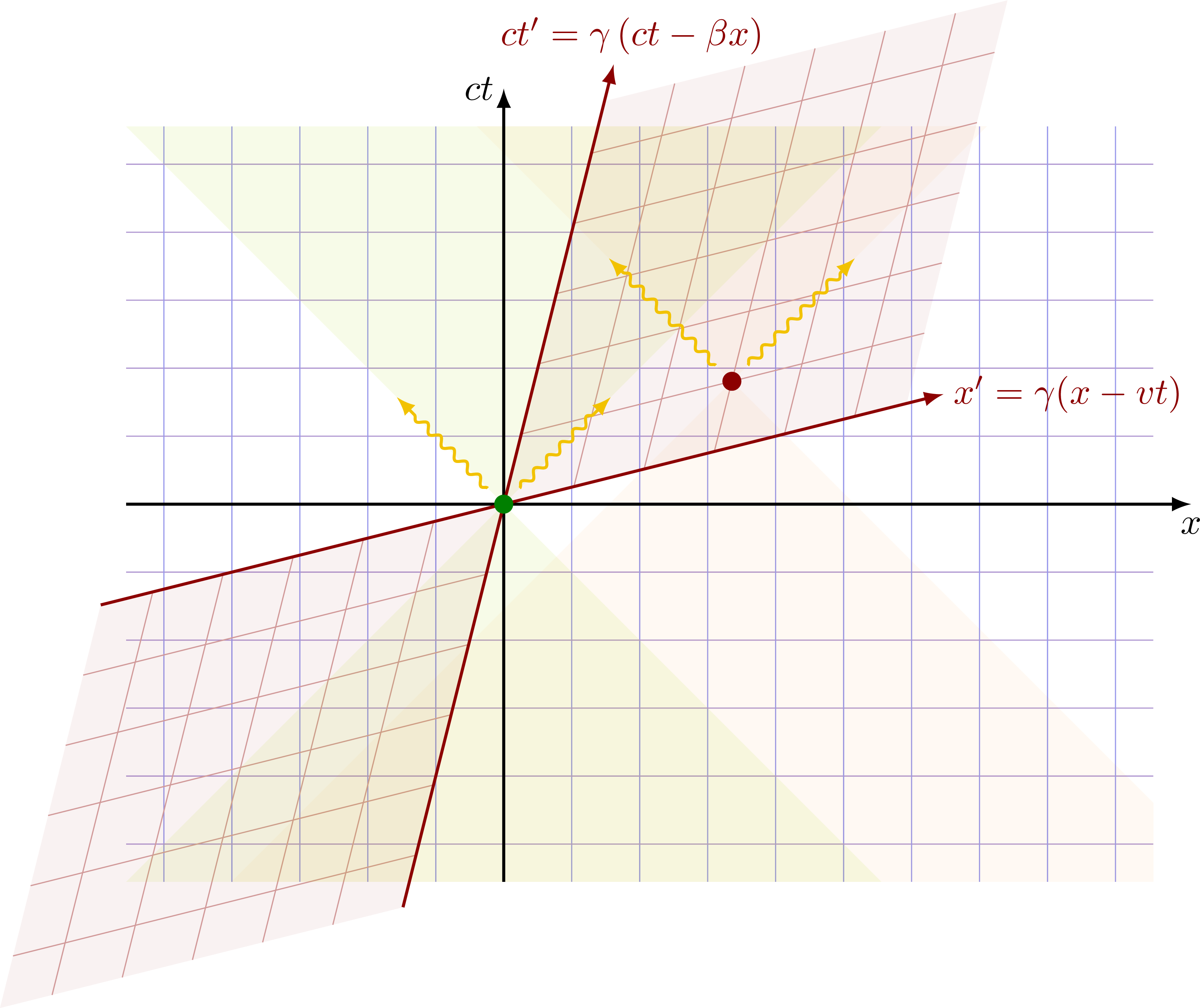
Lorentz transformation, or “boost”. Notice that the angle θ is given by the slope β = v/c = tanθ.
Inverse Lorentz transformation, or equivalently, if the boosted frame is moving to the left (in the negative x direction).
Simultaneity
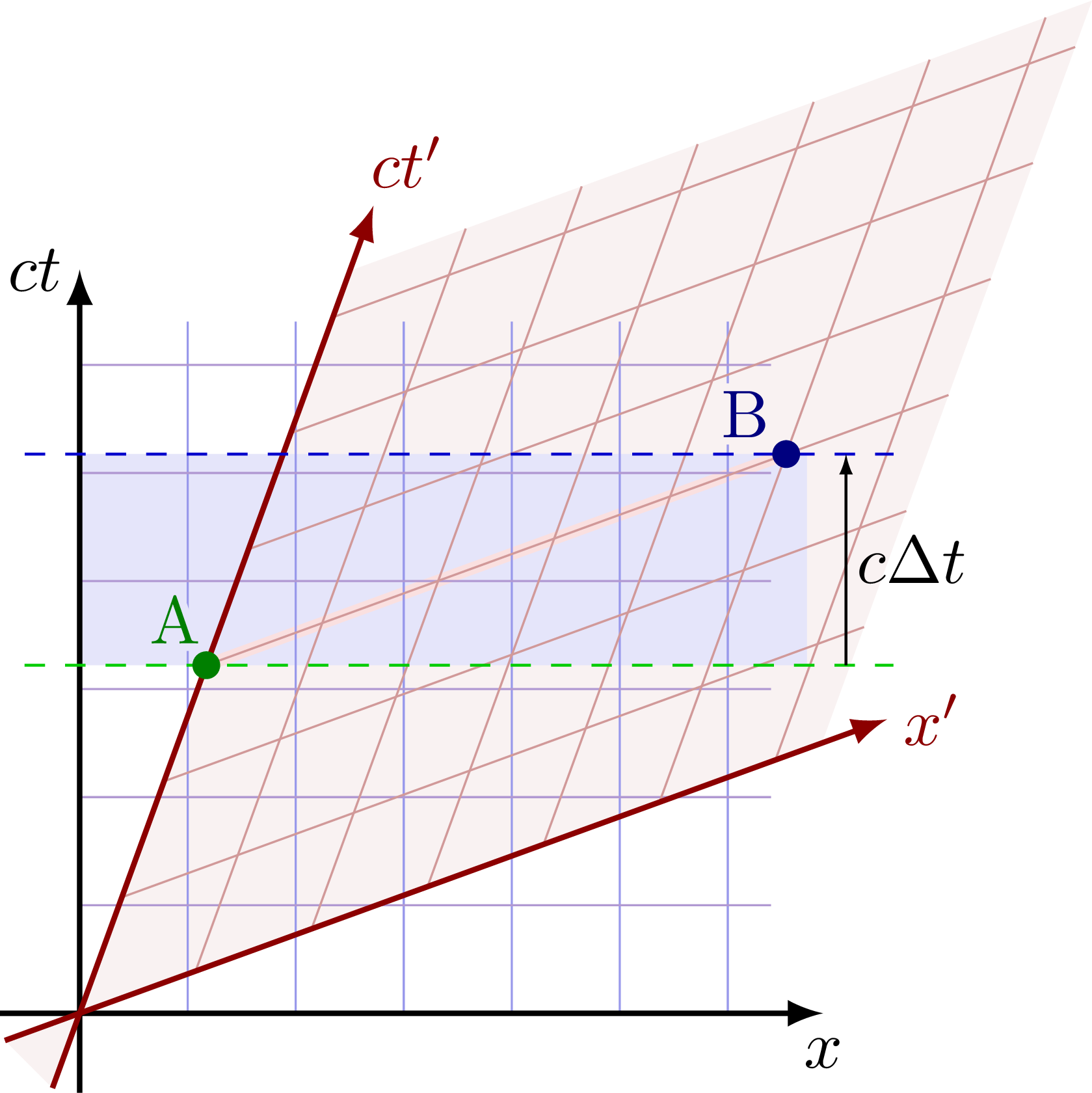
Events A and B are simultaneous in the rest frame S, but in the boosted frame S’, B happens before A.
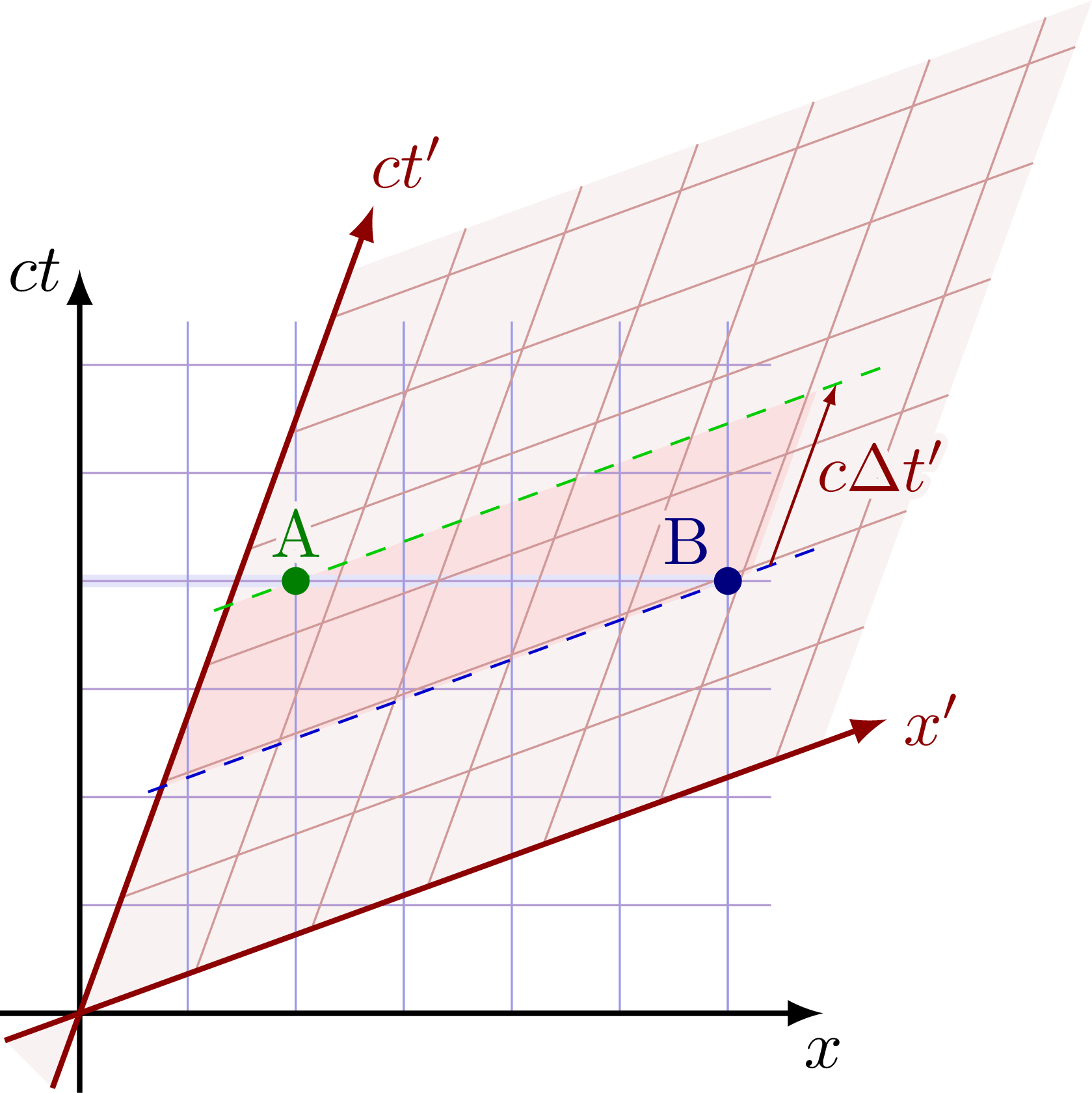
Events A and B are simultaneous in the boosted frame S’, but in the rest frame S, A happens before B.
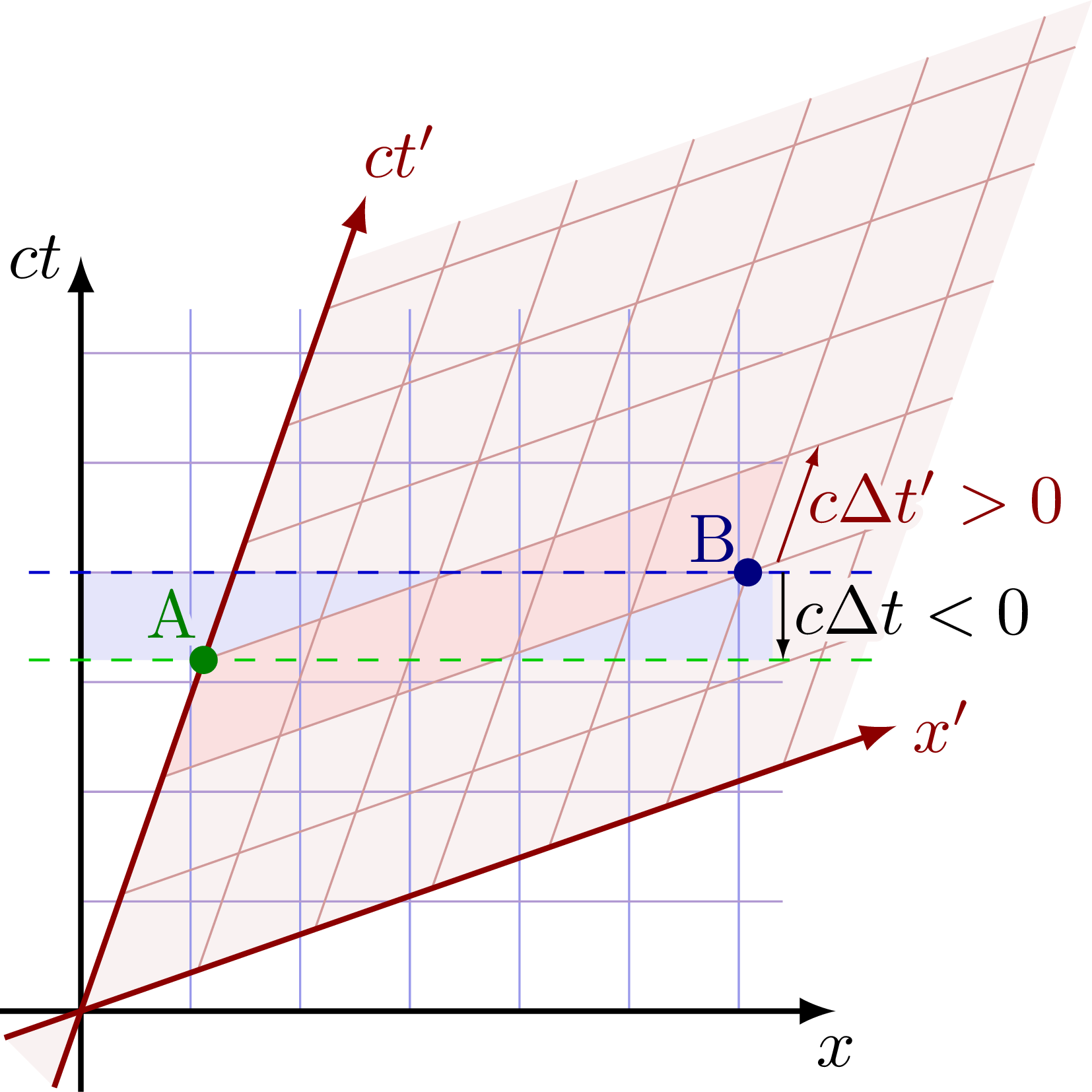
Relativity of simultaneity. Two observers experience events at in different order: In frame S, A happens before B, while in frame S’, B happens before A.
Time dilation
Time dilation in the boosted frame S’ for events at a fixed point of space in frame S. The time separation between A and B is longer in S’ than in S; Δt’ > Δt. The derivation is given in these lecture notes.
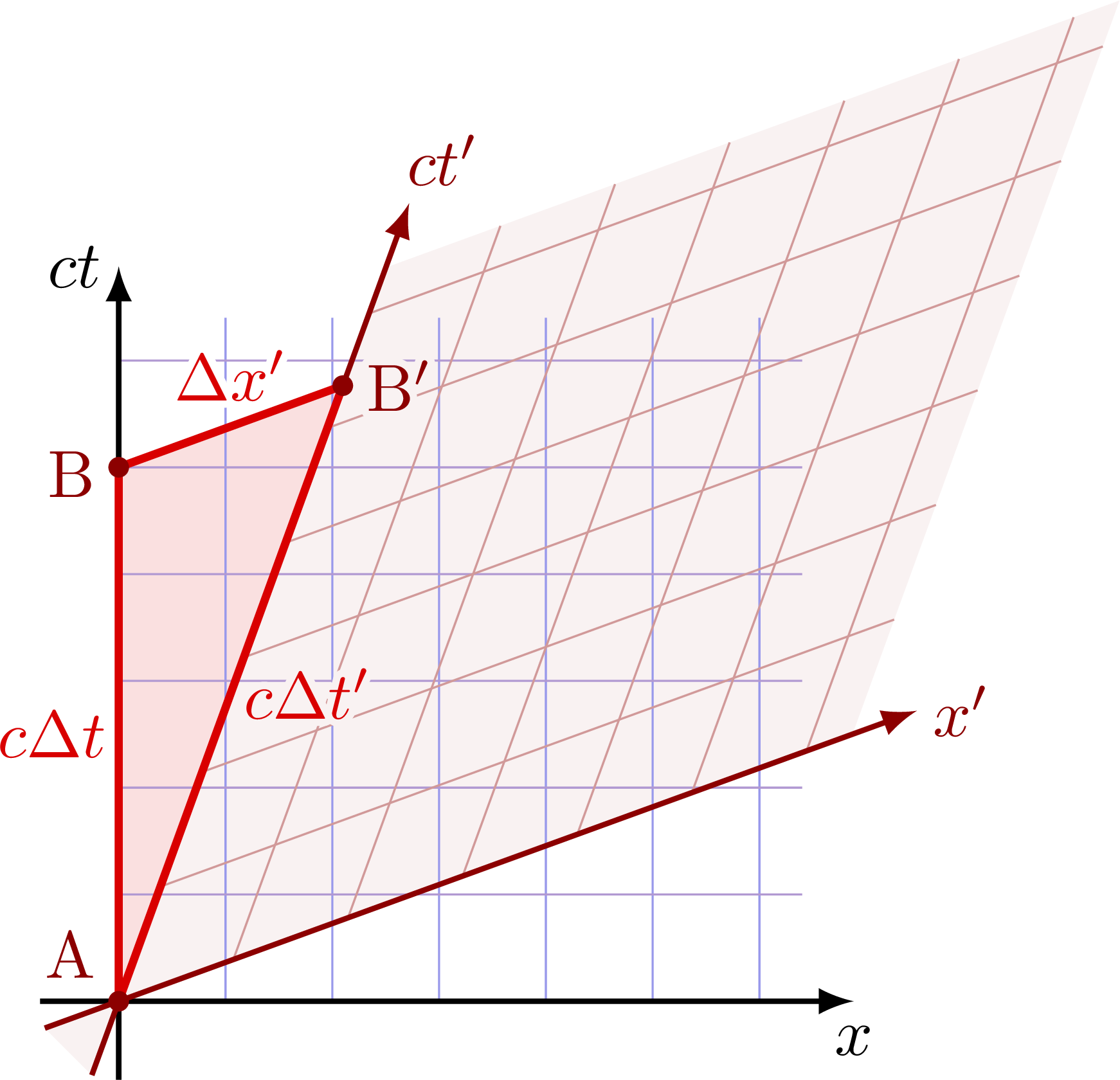
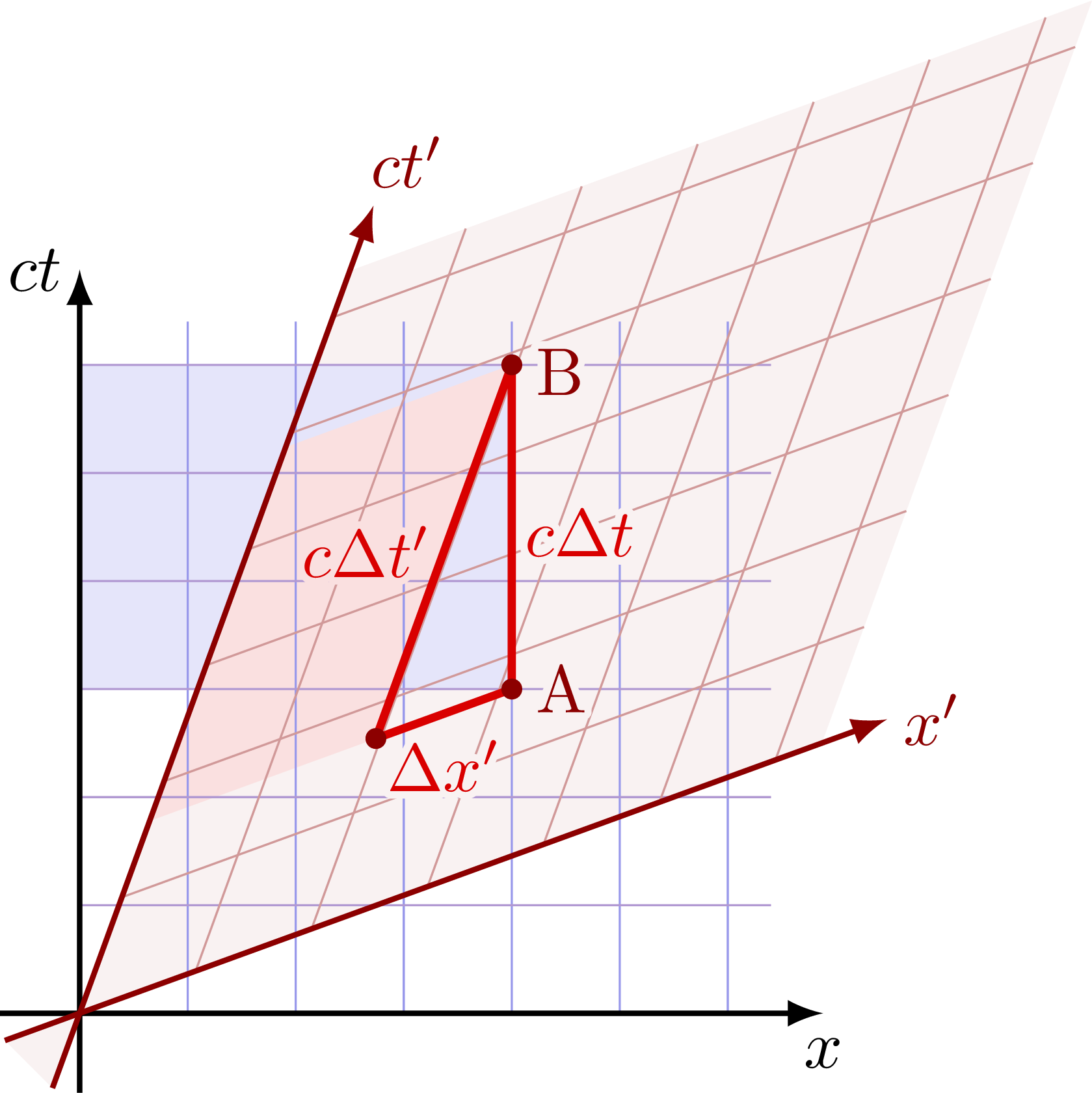
Time dilation for events at a fixed point of space in the boosted frame S’. The time separation between A and B is longer in S than in S’; Δt > Δt’.
Length contraction
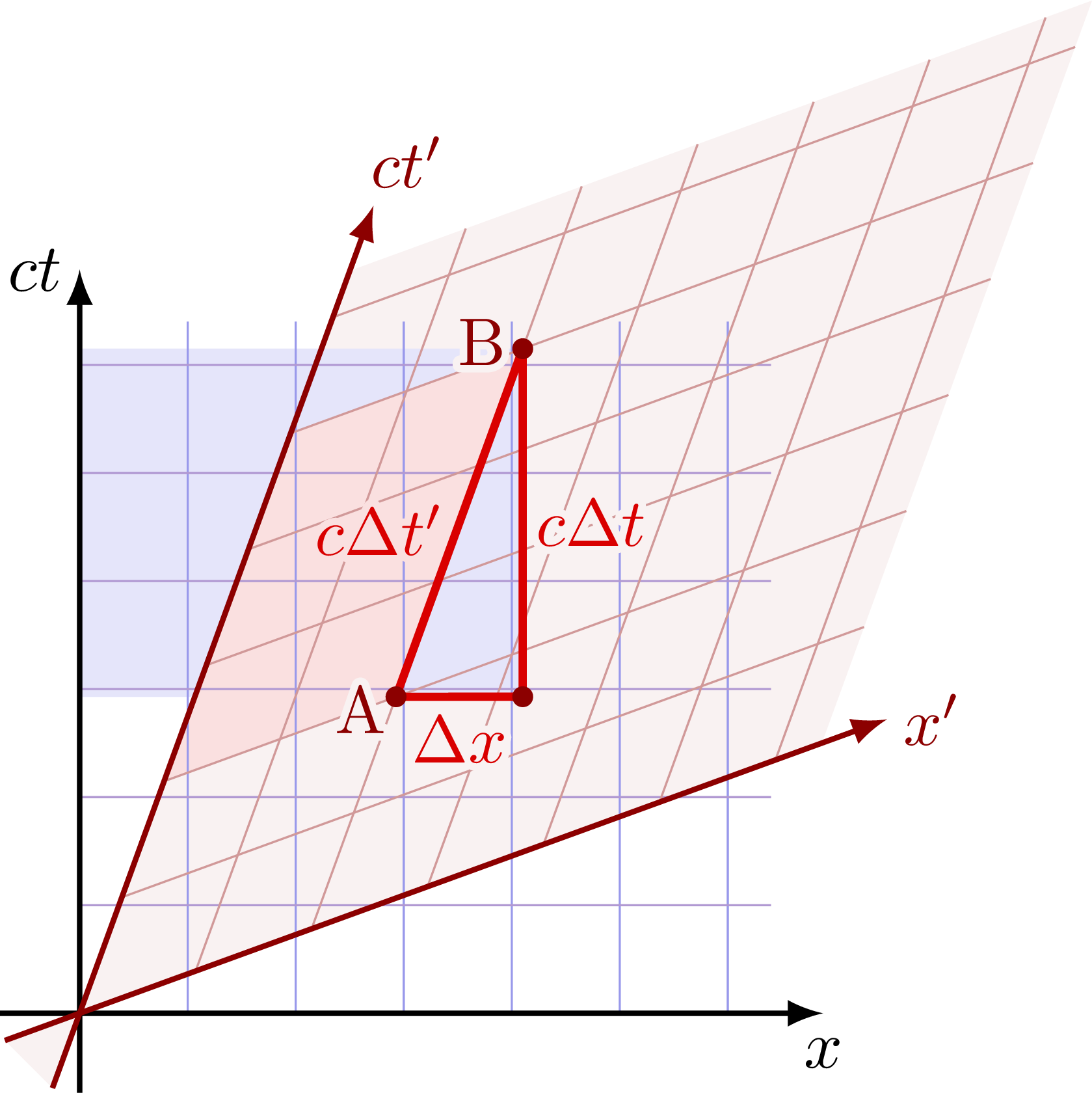
Length contraction of a rod at rest in frame S. The rod is shorter in the boosted frame S’, because it is moving relative to this frame. The derivation is given in these lecture notes.
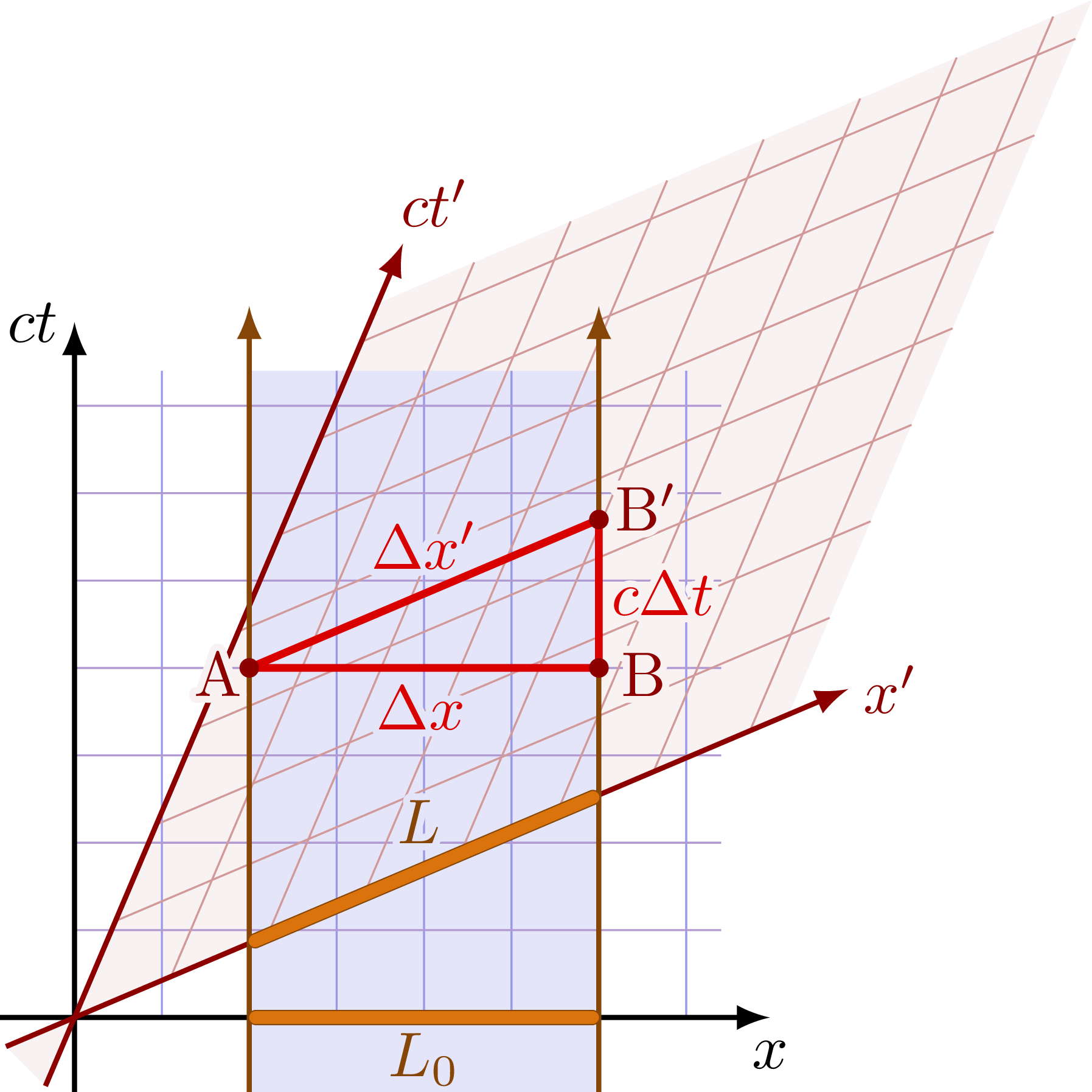
Length contraction of a rod moving in frame S. The rod is shorter in the frame S’, because it is moving relative to this frame.
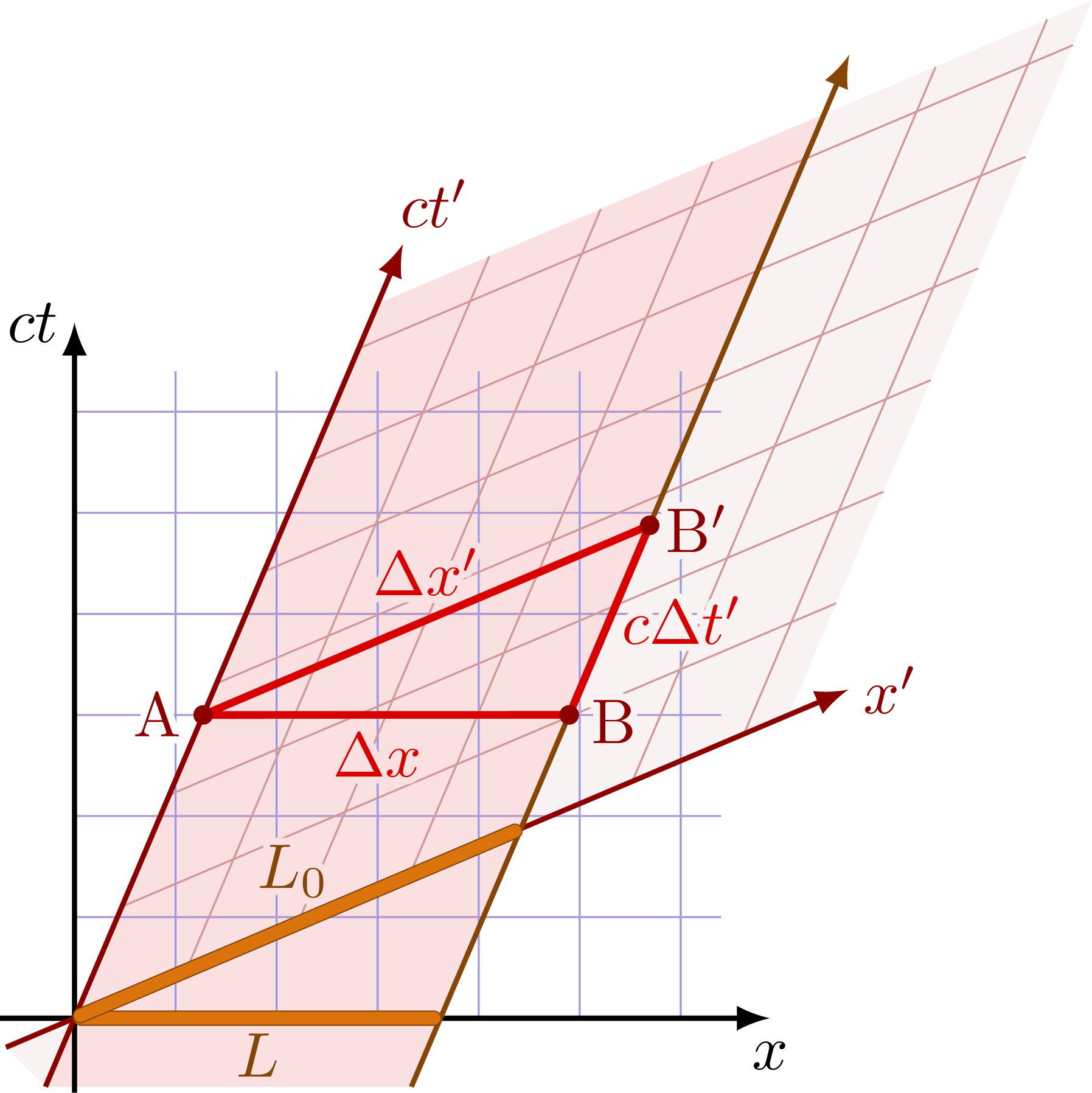
Paradoxes
Ladder paradox: Due to length-contraction a long ladder moving at relativistic speed is short enough to fit in a barn with both doors simultaneously closed. In the moving frame S’, however, the barn is contracted and cannot fit the ladder. The solution to the paradox is that the doors are never simultaneously closed in S’ due to the relativity of simultaneity.
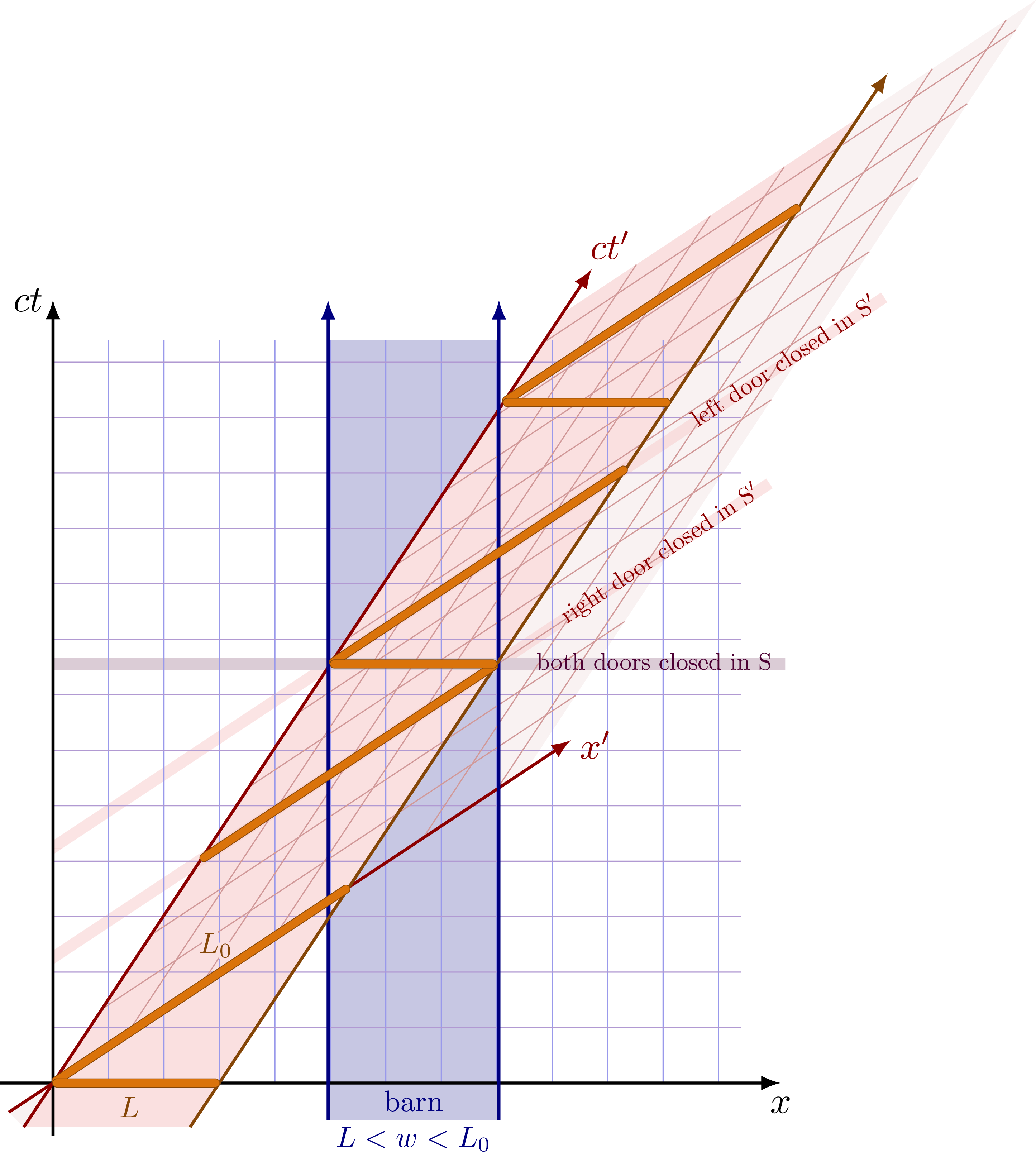
From the perspective of the observer in their rest frame S’, the barn is moving, and the doors are not closed simultaneously:
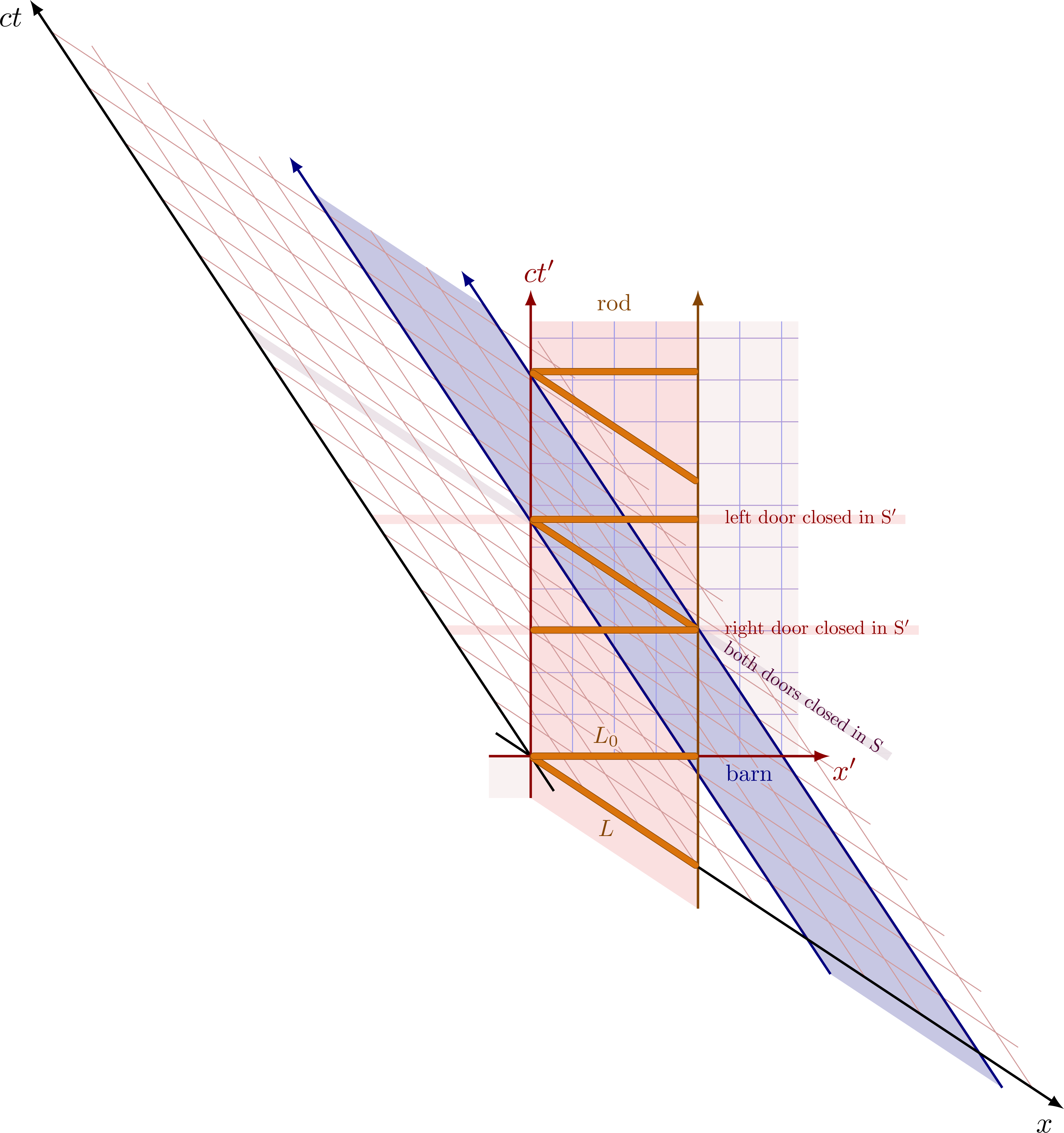
Twin paradox explained with planes of simultaneity.
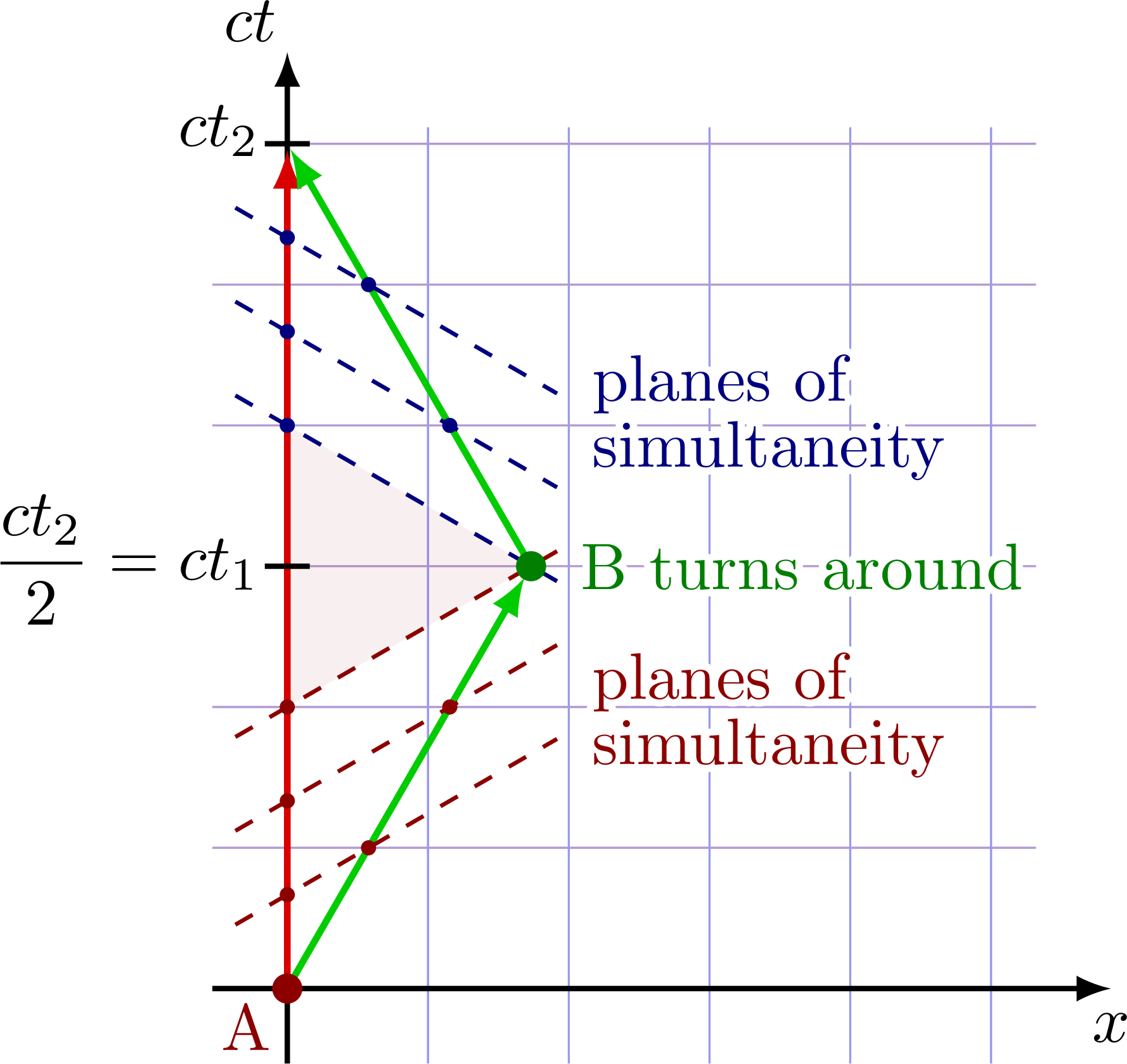
Hyperbolae
Hyperbolae in Minkowski spacetime to derive the Lorentz transformation in terms of hyperbolic functions sinh and cosh in analogy to rotation. The red point is boosted along the red hyperbola, such that its spacetime seperation from the origin remains constant.
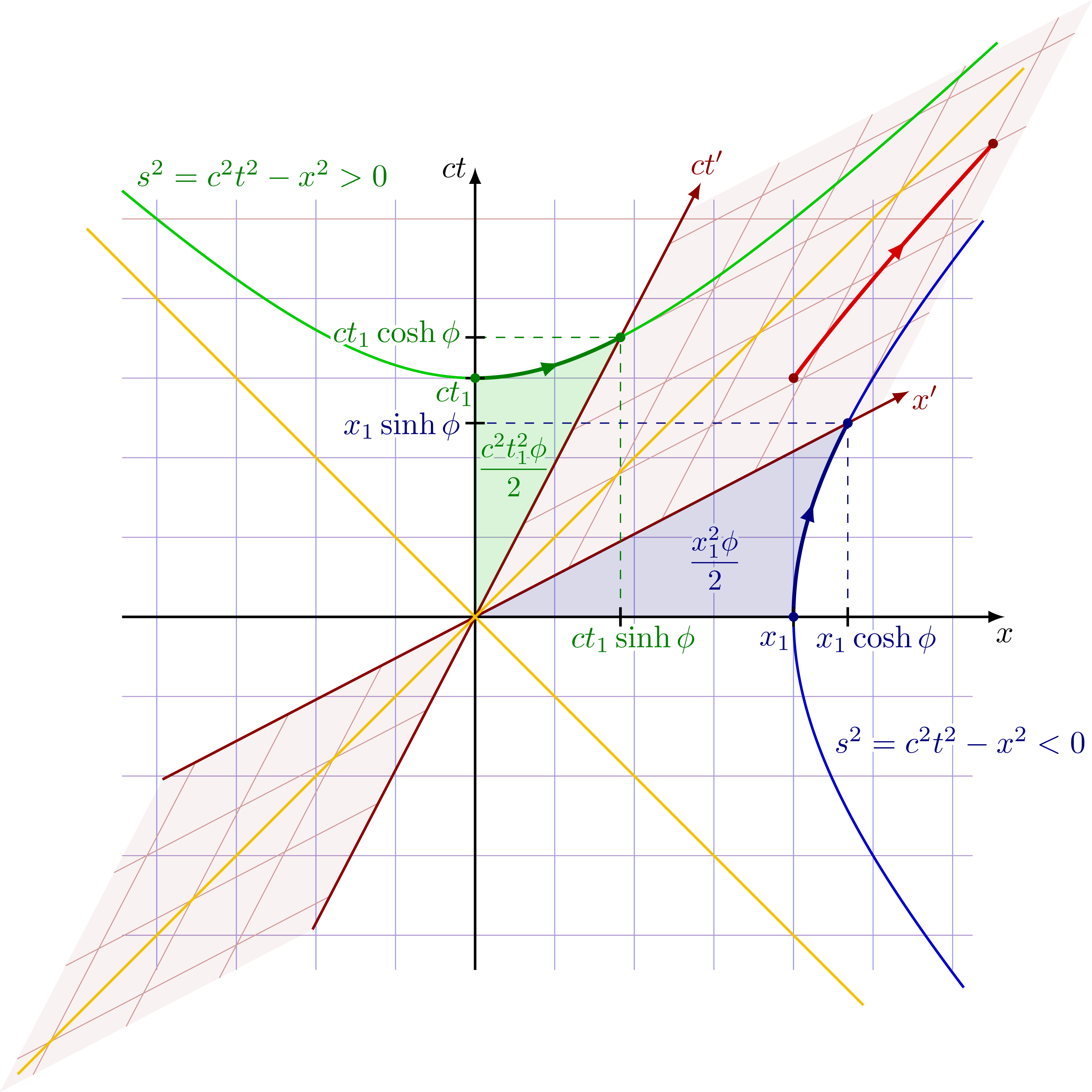
Equations for Lorentz transformation in terms of hyperbolic functions:
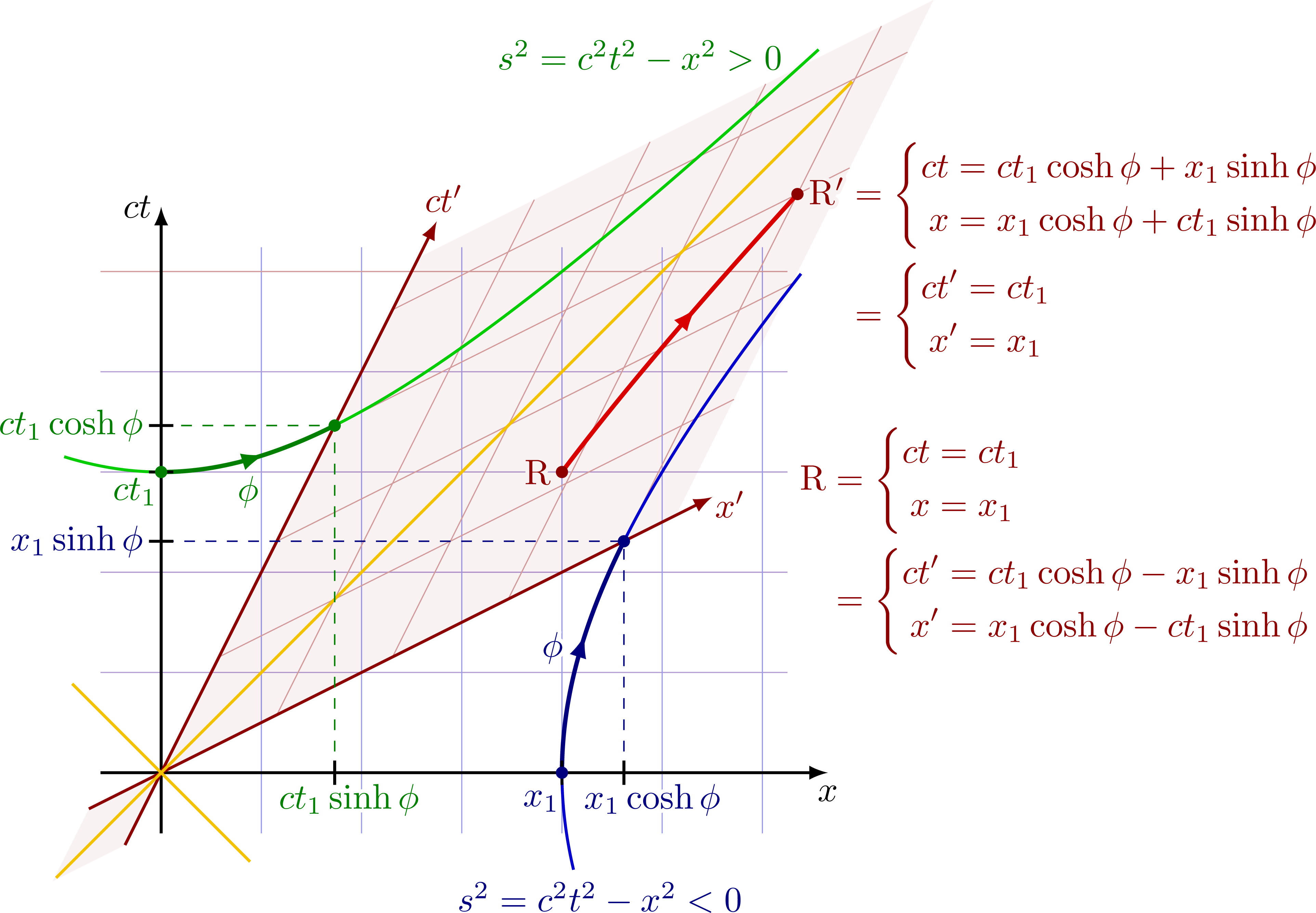
Equations for Lorentz transformation in terms of the γ factor and β = v/c:
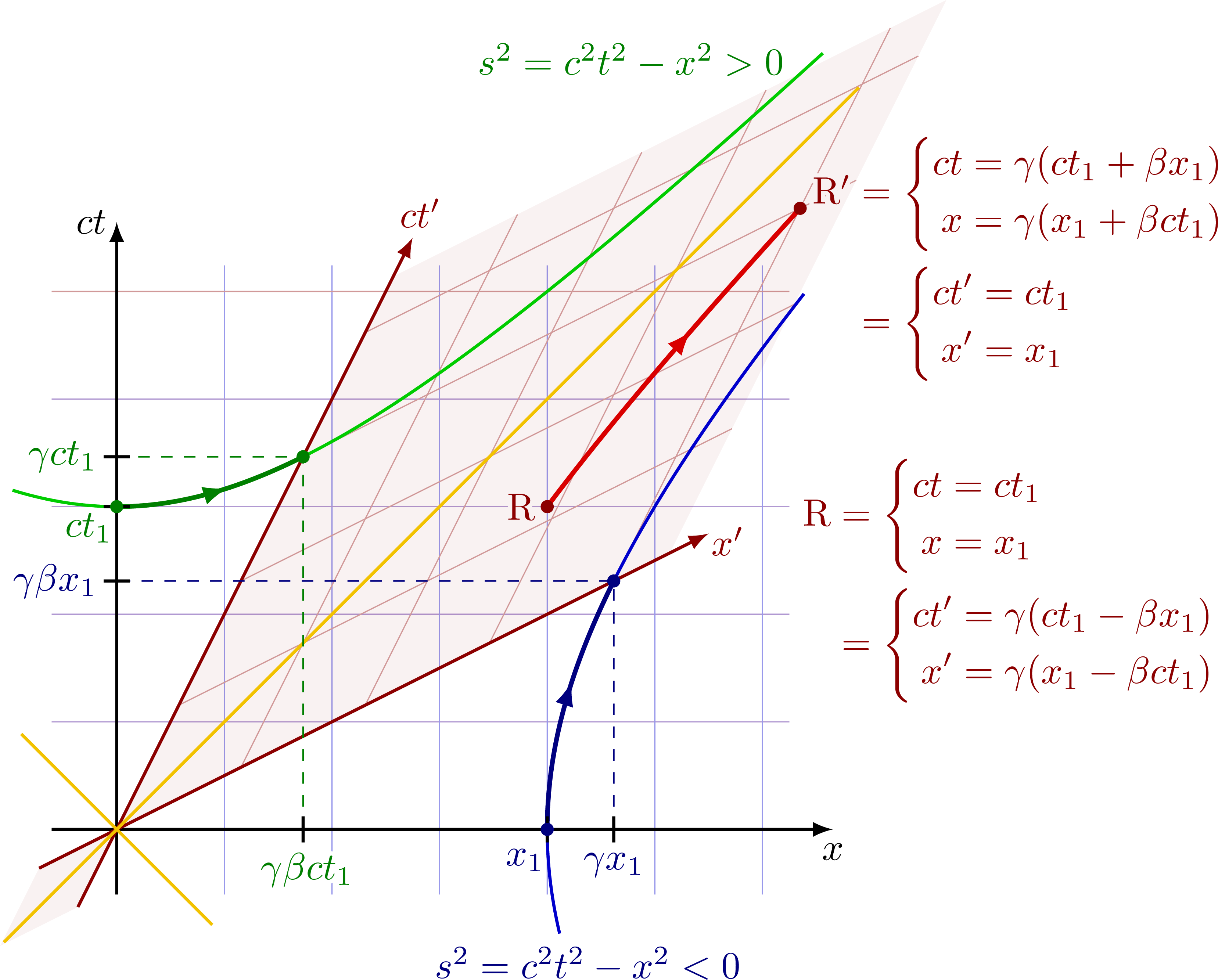
Lorentz transformation matrix with hyperbolic functions sinh and cosh in analogy to the rotation matrix. A boost is a hyperbolic rotation with rapidity 𝜑, where 𝛽 = tanh 𝜑.
Different hyperbolae in Minkowski spacetime. All points on the same hyperbola have an equal spacetime separation s from the origin (t,x) = (0,0). A boost (i.e. a hyperbolic rotation) moves a point along such a hyperbola, and therefore preserves the spacetime distance (i.e. spacetime distance between two points are invariant under Lorentz transformations).
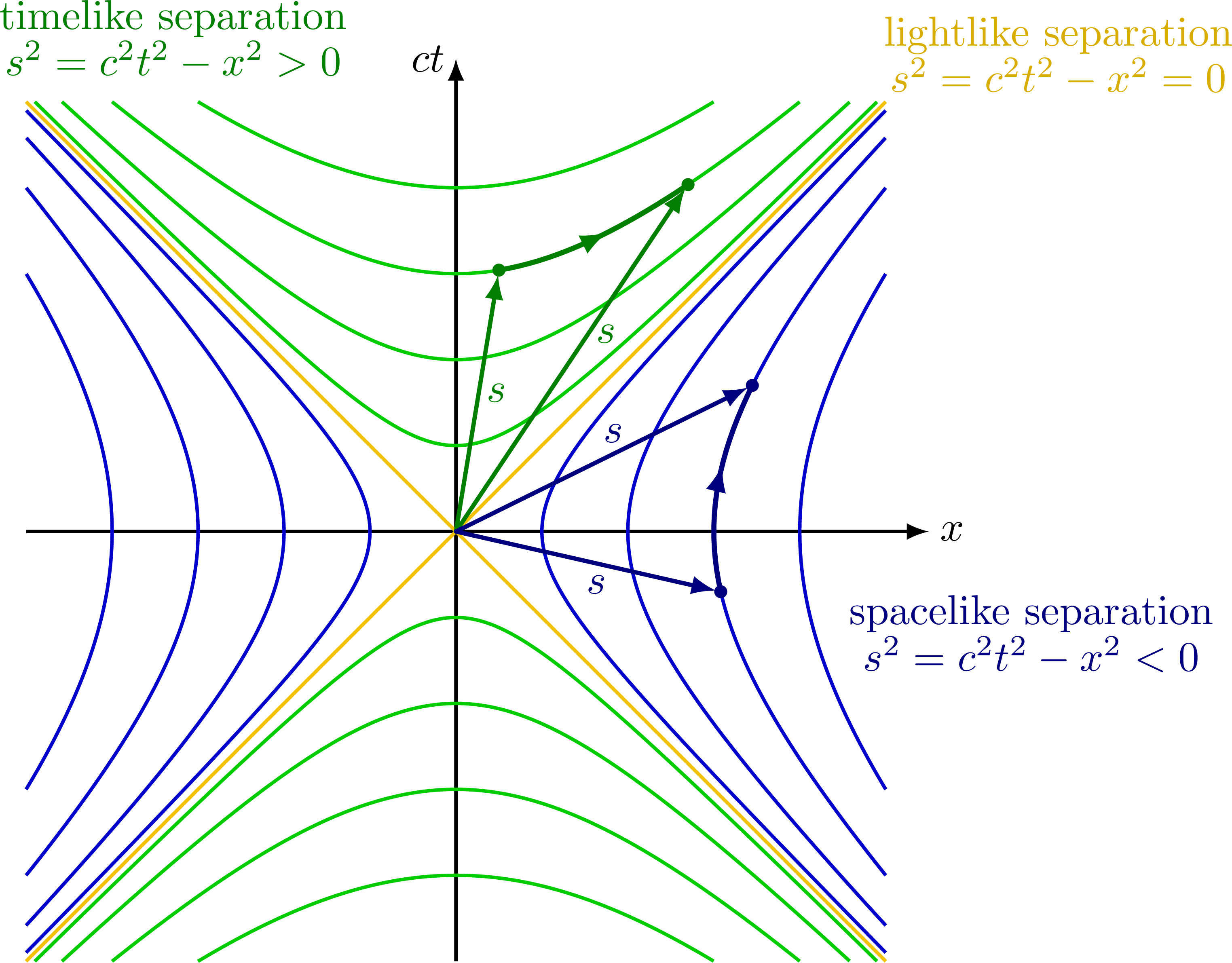
Notice that spacelike separation squared are negative, s2 < 0, so this distance will be imaginary, while timeline separations will be real.
Analogy to Euclidean rotation
Both boosts and rotations preserve the spacetime distance given by the metric ds2 = cdt2 – dx2 – dy2 – dz2. They are part of the so-called Lorentz group.
The transformation matrix for boosts in terms of hyperbolic functions looks very similar to the rotation matrix.
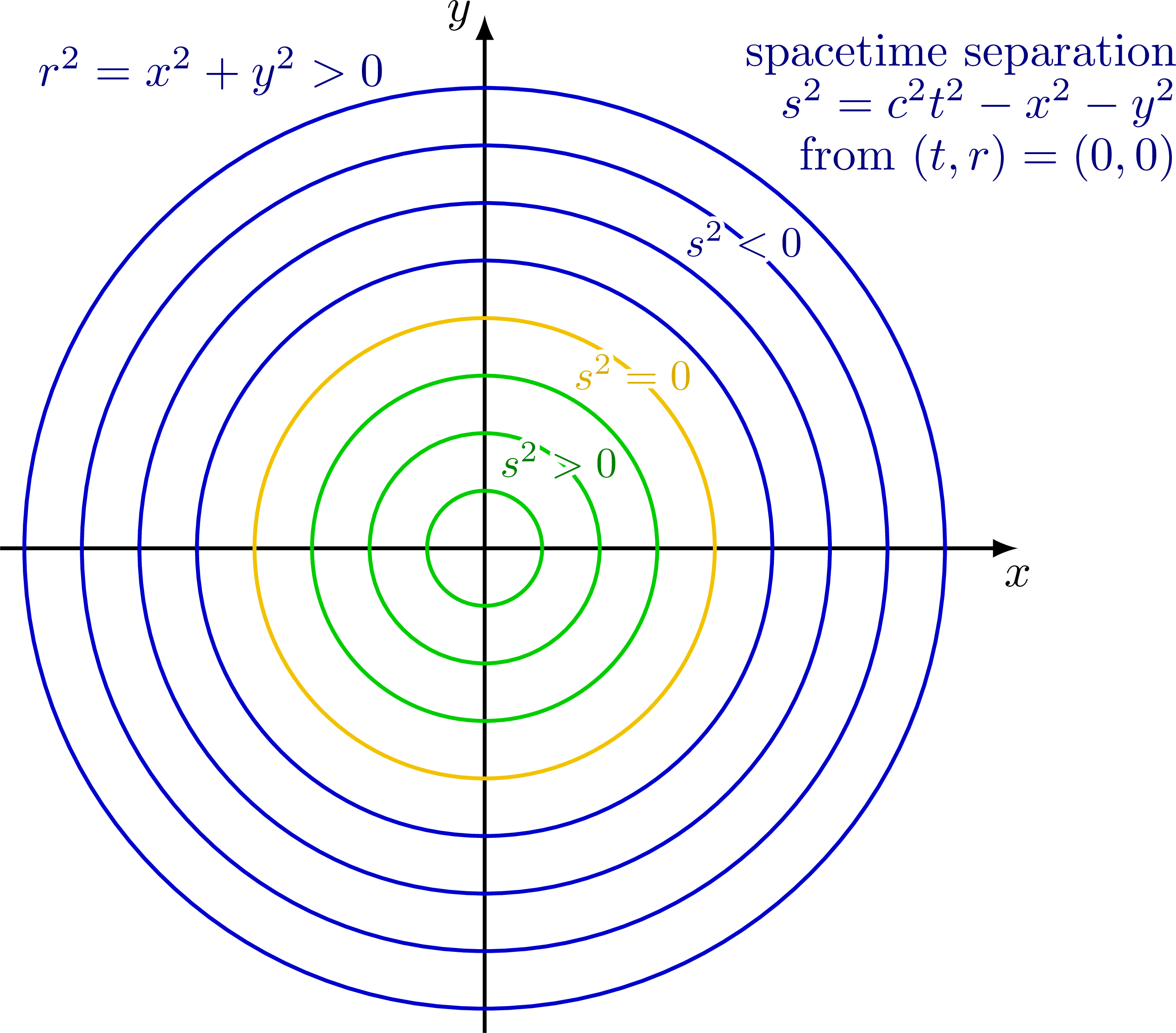
The 2D rotation matrix in the xy plane can be expressed as follows:
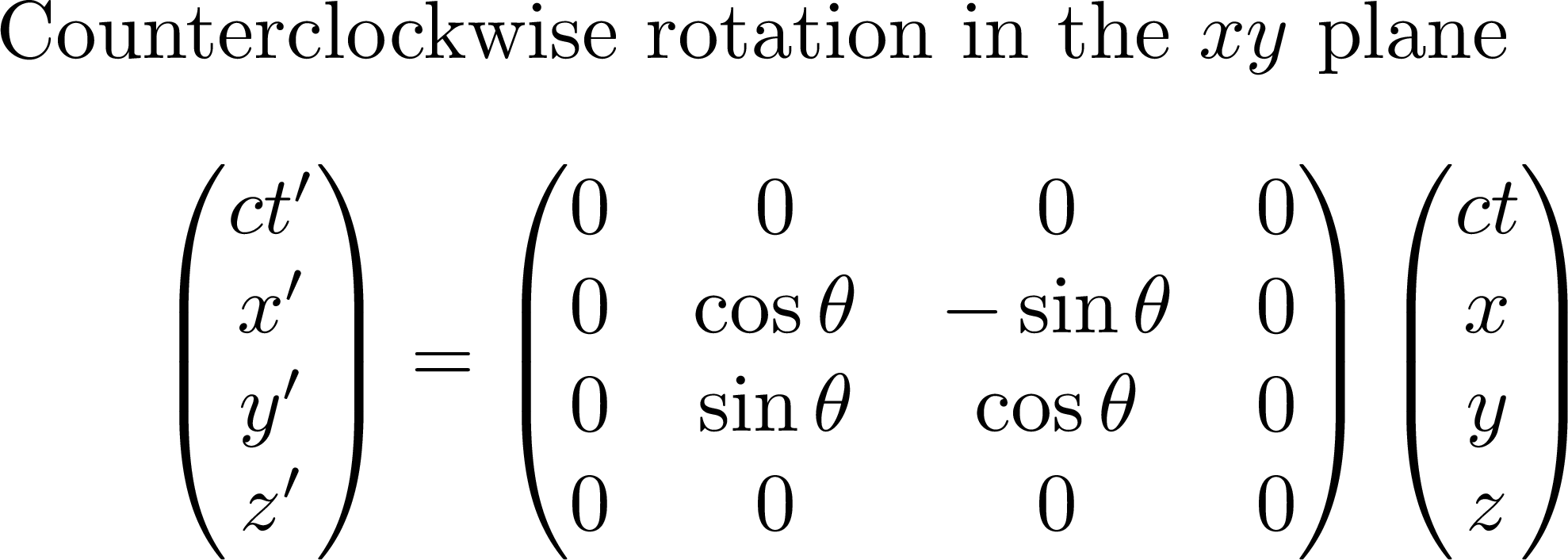
Spacelike slice at t = 0. All points on the same circle have the same (Euclidean) distance r to the origin. Euclidean rotations move points along the circle, and hence preserve this spacetime distance.
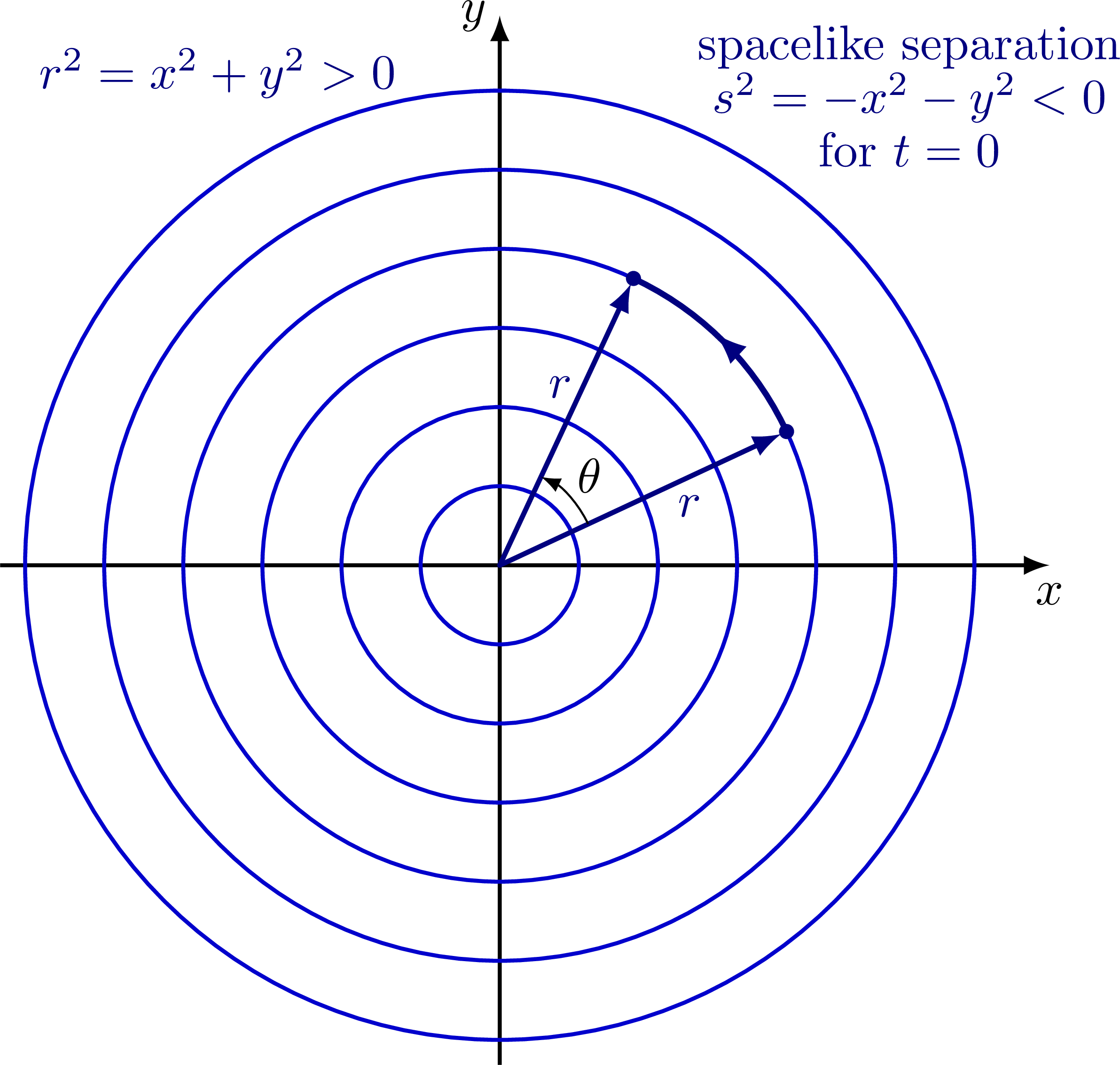
Spacelike slice to illustrate different types of separations.
Lorentz factor
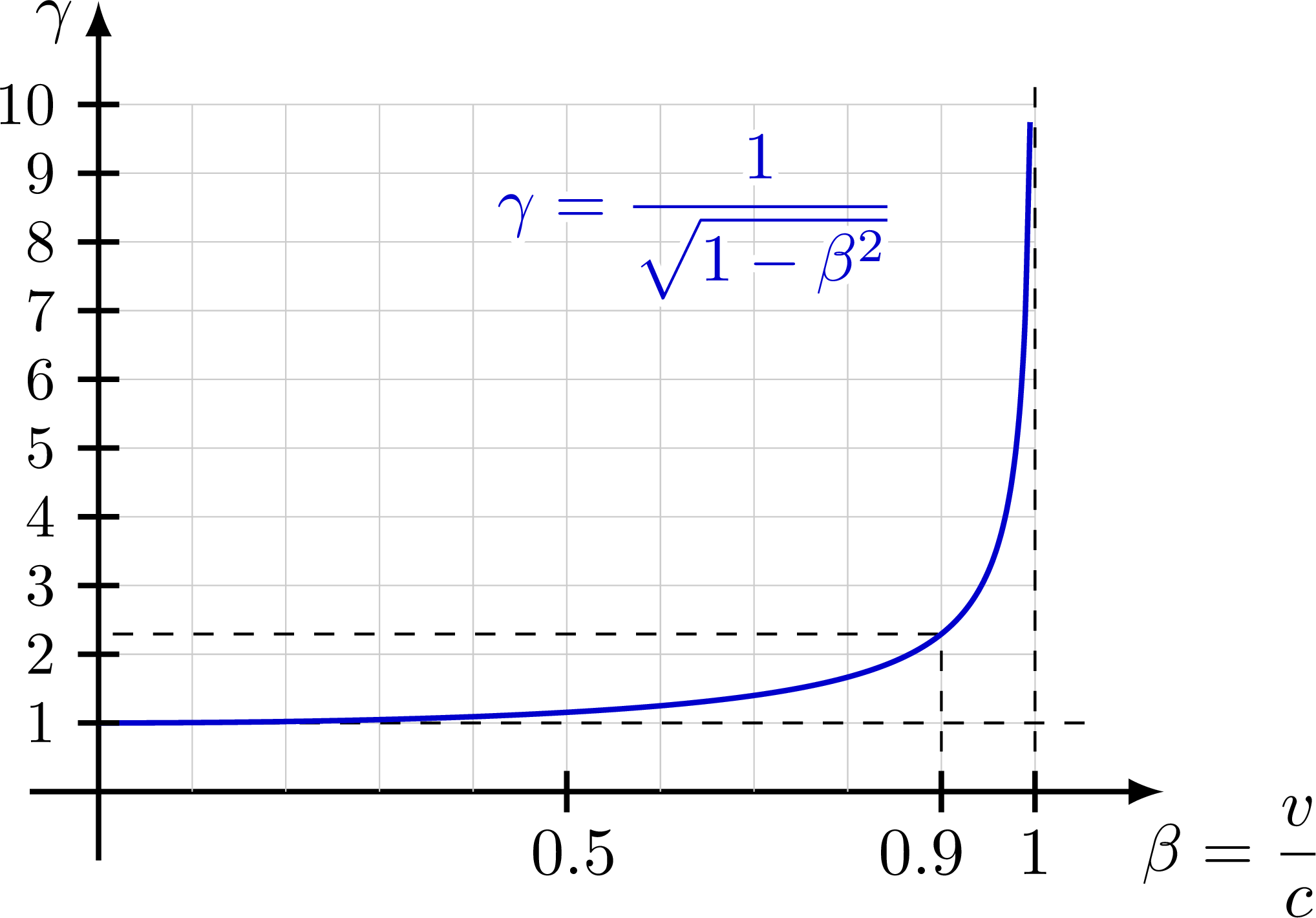
Plot of the Lorentz factor as a function of velocity v.
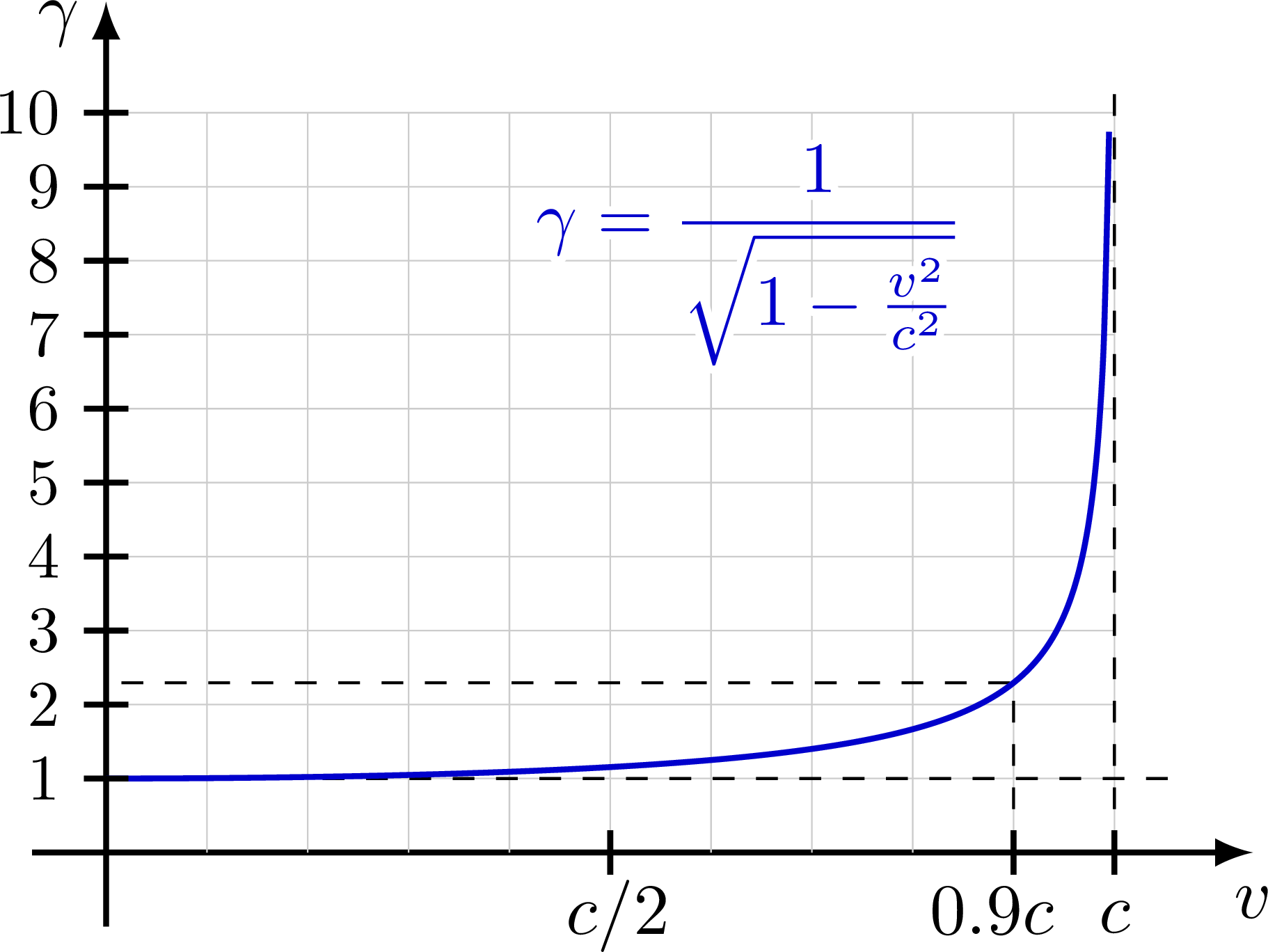
Plot of the Lorentz factor as a function of velocity β = v/c (i.e. in units of c).
Full code
Edit and compile if you like:
% Author: Izaak Neutelings (October 2021)
% Inspiration
% "Very special relativity - An illustrated guide", Sander Bais (2007)
% http://people.uncw.edu/hermanr/GR/Minkowski/Minkowski.pdf
\documentclass[border=3pt,tikz]{standalone}
\usepackage{amsmath} % for \text
\usepackage{etoolbox} % ifthen
\usepackage[outline]{contour} % glow around text
\usetikzlibrary{calc} % for adding up coordinates
\usetikzlibrary{decorations.markings,decorations.pathmorphing}
\usetikzlibrary{angles,quotes} % for pic (angle labels)
\usetikzlibrary{arrows.meta} % for arrow size
\usepackage{xfp} % higher precision (16 digits?)
\contourlength{1.1pt}
\tikzset{>=latex} % for LaTeX arrow head
\colorlet{myred}{red!85!black}
\colorlet{mydarkred}{red!55!black}
\colorlet{mylightred}{red!85!black!12}
\colorlet{myfieldred}{mydarkred!5} % for S' background
\colorlet{myredhighlight}{myred!20} % highlights simultaneity in ladder paradox
\colorlet{myblue}{blue!80!black}
\colorlet{mydarkblue}{blue!50!black}
\colorlet{mylightblue}{blue!50!black!30}
\colorlet{mylightblue2}{myblue!10}
\colorlet{mygreen}{green!80!black}
\colorlet{mypurple}{blue!40!red!80!black}
\colorlet{mydarkgreen}{green!50!black}
\colorlet{mydarkpurple}{blue!40!red!50!black}
\colorlet{myorange}{orange!40!yellow!95!black}
\colorlet{mydarkorange}{orange!40!yellow!85!black}
\colorlet{mybrown}{brown!20!orange!90!black}
\colorlet{mydarkbrown}{brown!20!orange!55!black}
\colorlet{mypurplehighlight}{mydarkpurple!20} % highlights simultaneity in ladder paradox
\tikzstyle{world line}=[myblue!40,line width=0.3]
\tikzstyle{world line t}=[mypurple!50!myblue!40,line width=0.3]
\tikzstyle{world line'}=[mydarkred!40,line width=0.3]
\tikzstyle{mysmallarr}=[-{Latex[length=3,width=2]},thin]
\tikzstyle{mydashed}=[dash pattern=on 3 off 3]
\tikzstyle{rod}=[mydarkbrown,draw=mydarkbrown,double=mybrown,double distance=2pt,
line width=0.2,line cap=round,shorten >=1pt,shorten <=1pt]
%\tikzstyle{rod'}=[rod,draw=mydarkbrown!80!red!85,double=mybrown!80!red!85]
\tikzstyle{vector}=[->,line width=1,line cap=round]
\tikzstyle{vector'}=[vector,shorten >=1.2]
\tikzstyle{particle}=[mygreen,line width=0.9]
\tikzstyle{photon}=[-{Latex[length=5,width=4]},myorange,line width=0.8,decorate,
decoration={snake,amplitude=1.0,segment length=5,post length=5}]
\def\tick#1#2{\draw[thick] (#1) ++ (#2:0.06) --++ (#2-180:0.12)}
\def\tickp#1#2{\draw[thick,mydarkred] (#1) ++ (#2:0.06) --++ (#2-180:0.12)}
\def\Nsamples{100} % number samples in plot
\begin{document}
% SPACETIME DIAGRAM
\begin{tikzpicture}[scale=1.8]
\message{Basic spacetime diagram^^J}
\def\xmax{2}
\def\Nlines{4} % number of world lines (at constant x/t)
% WORLD LINES GRID
\message{ Making world lines...^^J}
\foreach \i [evaluate={\x=\i*0.9*\xmax/\Nlines;}] in {1,...,\Nlines}{
\message{ Running i/N=\i/\Nlines, x=\x...^^J}
\draw[world line] (-\x,-\xmax) -- (-\x,\xmax);
\draw[world line] ( \x,-\xmax) -- ( \x,\xmax);
\draw[world line t] (-\xmax,-\x) -- (\xmax,-\x);
\draw[world line t] (-\xmax, \x) -- (\xmax, \x);
}
% AXES
\draw[->,thick] (0,-\xmax) -- (0,\xmax+0.2) node[left=-1] {$ct$};
\draw[->,thick] (-\xmax,0) -- (\xmax+0.2,0) node[below=0] {$x$};
\end{tikzpicture}
% SPACETIME DIAGRAM with WORLD LINES
\begin{tikzpicture}[scale=2.0]
\message{Worldlines^^J}
\def\ymin{0.2}
\def\xmin{1.6}
\def\xmax{2}
\def\Nlines{4} % number of world lines (at constant x/t)
\pgfmathsetmacro\d{0.9*\xmax/\Nlines} % grid size
\coordinate (O) at (0,0);
\coordinate (T) at (0,\xmax+0.2);
% WORLD LINES GRID
\message{ Making world lines...^^J}
\foreach \i [evaluate={\x=\i*\d;}] in {1,...,\Nlines}{
\message{ Running i/N=\i/\Nlines, x=\x...^^J}
\draw[world line] ( \x,-\ymin) -- ( \x,\xmax);
\draw[world line t] (-\xmin, \x) -- (\xmax, \x);
}
\draw[world line] (-\d,-\ymin) -- (-\d,\xmax);
\draw[world line] (-2*\d,-\ymin) -- (-2*\d,\xmax);
\draw[world line] (-3*\d,-\ymin) -- (-3*\d,\xmax);
% AXES
\draw[->,thick] (0,-\ymin) -- (T) node[left=-1] {$ct$};
\draw[->,thick] (-\xmin,0) -- (\xmax+0.2,0) node[below=0] {$x$};
% VECTORS
\draw[vector,myorange] (O) -- (135:0.78*\xmax)
node[mydarkorange,left=6,above=-3] {\contour{white}{$x(t)=-ct$}};
\draw[vector,myblue] (O) -- ({atan(1/2)}:1.12*\xmax) %(45/2:\xmax)
node[mydarkblue,anchor=-155,outer sep=-1] {$x(t)=2ct$};
\draw[vector,myorange] (O) -- (45:1.08*\xmax)
node[mydarkorange,left=1,above right=-2] {\contour{white}{$x(t)=ct$}};
\draw[vector,mypurple] (O) -- (55:1.2*\xmax)
node[mydarkpurple,right=10,above] {\contour{white}{$x(t)=vt$}};
\draw[vector,mygreen]
(-0.10*\xmax,-0.12*\xmax) to[out=35,in=-100] (O)
to[out=80,in=-80,looseness=1.5] (0.3*\xmax,1.05*\xmax)
node[mydarkgreen,above=-3] {\contour{white}{$x(t)=v(t)t$}};
\draw[vector,myred] (O) -- (0,0.88*\xmax)
node[mydarkred,below left=0] {\contour{white}{$x(t)=0$}};
%\node[right=8,above,mydarkpurple] at (T) {$x(t)=0$};
\end{tikzpicture}
% SPACETIME DIAGRAM with TWO OBSERVERS
\begin{tikzpicture}[scale=2.0]
\message{Two observers^^J}
\def\xmin{0.2}
\def\xmax{2}
\def\R{2.03} % vector length
\def\Nlines{4} % number of world lines (at constant x/t)
\pgfmathsetmacro\d{0.9*\xmax/\Nlines} % grid size
\pgfmathsetmacro\D{2*\d} % distance between observers
\coordinate (A) at (0,0); % observer A at t=0
\coordinate (B) at (\D,0); % observer B at t=0
\coordinate (C) at (2*\d,2*\d); % point of reflection
\coordinate (T1) at (0,2*\d); % time of reflection
\coordinate (T2) at (0,4*\d); % light returning at x=0
% WORLD LINES GRID
\message{ Making world lines...^^J}
\foreach \i [evaluate={\x=\i*\d;}] in {1,...,\Nlines}{
\message{ Running i/N=\i/\Nlines, x=\x...^^J}
\draw[world line] ( \x,-\xmin) -- ( \x,\xmax);
\draw[world line t] (-\xmin, \x) -- (\xmax, \x);
}
% AXES
\draw[->,thick] (0,-\xmin) -- (0,\xmax+0.2) node[above left=-2] {$ct$};
\draw[->,thick] (-\xmin,0) -- (\xmax+0.2,0) node[below=0] {$x$};
\draw[thick,mydarkred,dashed] (T1) -- (C);
\draw[thick,mydarkred,dashed] (T2) -- (2*\d,4*\d);
% VECTORS
\draw[vector,myred] (A) --++ (0,\R)
node[mydarkred,above=-2,left=-1] {\contour{white}{$x_\mathrm{A}=0$}};
\draw[vector,mygreen] (B) --++ (0,\R)
node[mydarkgreen,left=1,above=-4] {\contour{white}{$x_\mathrm{B}'=d$}};
\draw[photon,shorten >=1] (C) -- (T2);
\fill[mydarkorange] (C) circle(0.04);
\draw[photon,shorten >=2] (A) -- (C);
\fill[mydarkred] (A) circle(0.04) node[below left=-1] {A}; % observer A
\fill[mydarkgreen] (B) circle(0.04) node[fill=white,inner sep=0.5,below=2.5] {B}; % observer B
% TICKS
\node[fill=white,inner sep=1,left=3] at (T1) {$\dfrac{ct_2}{2}=ct_1$};
\node[fill=white,inner sep=1,left=3] at (T2) {$ct_2$};
\tick{T1}{0};
\tick{T2}{0};
\end{tikzpicture}
% SPACETIME DIAGRAM with TWO MOVING OBSERVERS to show simultaneity
\begin{tikzpicture}[scale=2.0]
\message{Two moving observers^^J}
\def\xmin{0.2}
\def\xmax{2}
\def\R{2.3} % vector length
\def\Nlines{4} % number of world lines (at constant x/t)
\pgfmathsetmacro\ang{73} % angle between ct and ct' axes
\pgfmathsetmacro\d{0.9*\xmax/\Nlines} % grid size
\pgfmathsetmacro\D{2*\d} % distance between observers
\coordinate (A) at (0,0); % observer A at t=0
\coordinate (B) at (\D,0); % observer B at t=0
\coordinate (C) at (45:{\D*sqrt(2)/(1-cot(\ang))}); % point of reflection
%\coordinate (T1) at (\ang:{2*\d/sin(\ang)/sqrt(1-cot(\ang)^2)}); % time of reflection
\coordinate (T1) at (\ang:{\D*sqrt(cot(\ang)^2+1)/(1-cot(\ang)^2)}); % time of reflection
\coordinate (T2) at (\ang:{2*\D*sqrt(cot(\ang)^2+1)/(1-cot(\ang)^2)}); % time of reflection
% WORLD LINES GRID
\message{ Making world lines...^^J}
\foreach \i [evaluate={\x=\i*\d;}] in {1,...,\Nlines}{
\message{ Running i/N=\i/\Nlines, x=\x...^^J}
\draw[world line] ( \x,-\xmin) -- ( \x,\xmax);
\draw[world line t] (-\xmin, \x) -- (\xmax, \x);
}
% AXES
\draw[->,thick] (0,-\xmin) -- (0,\xmax+0.2) node[above left=-2] {$ct$};
\draw[->,thick] (-\xmin,0) -- (\xmax+0.2,0) node[below=0] {$x$};
\draw[->,thick,mydarkred,dashed] (A) -- (90-\ang:\xmax) node[above=1,right=-1] {$x$}; %_\mathrm{A}'
\draw[->,thick,mydarkred,dashed] (T1) --++ (90-\ang:\xmax);
% VECTORS
\draw[vector,myred] (A) --++ (\ang:\R)
node[mydarkred,left=1,above=-2] {$x_\mathrm{A}=vt$};
\draw[vector,mygreen] (B) --++ (\ang:\R)
node[mydarkgreen,right=6,above=-2] {$x_\mathrm{B}=d+vt$};
\draw[photon,shorten >=1] (C) --++ (135:{\D*sqrt(2)/(1+cot(\ang))});
\fill[mydarkorange] (C) circle(0.04);
\draw[photon,shorten >=2] (A) -- (C);
\fill[mydarkred] (A) circle(0.04) node[below left=-1] {A}; % observer A
\fill[mydarkgreen] (B) circle(0.04) node[fill=white,inner sep=0.5,below=2.5] {B}; % observer B
% TICKS
%\node[fill=white,inner sep=1,left=3] at (T1) {$\dfrac{ct_2}{2}=ct_1$};
%\node[fill=white,inner sep=1,left=3] at (T2) {$ct_2$};
\tickp{T1}{90-\ang} node[left=-4] {\contour{white}{$\dfrac{ct_2'}{2}=ct_1'$}};
\tickp{T2}{90-\ang} node[left=-3] {\contour{white}{$ct_2'$}};
\end{tikzpicture}
% SPACETIME DIAGRAM - LIGHT CONE
\begin{tikzpicture}[scale=1.8]
\message{Light cone^^J}
\def\xmax{2}
\def\xmaxp{2.2} % maximum of rotated axis
\def\Nlines{5} % number of world lines (at constant x/t)
\pgfmathsetmacro\d{0.9*\xmax/\Nlines} % grid size
\pgfmathsetmacro\ang{atan(1/3)} % angle between x and x' axes
\coordinate (O) at (0,0);
\coordinate (X) at (\xmax+0.2,0);
\coordinate (T) at (0,\xmax+0.2);
% WORLD LINE GRID
\message{ Making world lines...^^J}
\foreach \i [evaluate={\x=\i*\d;}] in {1,...,\Nlines}{
\message{ Running i/N=\i/\Nlines, x=\x...^^J}
\draw[world line] (-\x,-\xmax) -- (-\x,\xmax);
\draw[world line] ( \x,-\xmax) -- ( \x,\xmax);
\draw[world line t] (-\xmax,-\x) -- (\xmax,-\x);
\draw[world line t] (-\xmax, \x) -- (\xmax, \x);
}
% AXES
\draw[->,thick] (0,-\xmax) -- (T) node[left=-1] {$ct$};
\draw[->,thick] (-\xmax,0) -- (X) node[below=0] {$x$};
% LABELS
\draw pic[->,"$45^\circ$",draw=black,angle radius=23,angle eccentricity=1.38] {angle = X--O--C};
\node[mydarkorange,above right] at (0.1*\xmax,\xmax) {future light cone};
\node[mydarkorange,below] at (0,-\xmax) {past light cone};
% FILLS
\fill[myblue,opacity=0.05] % SPACELIKE
(\xmax,\xmax) -- (-\xmax,-\xmax) -- (-\xmax,\xmax) -- (\xmax,-\xmax) -- cycle;
\fill[myorange,opacity=0.05] % TIMELIKE
(\xmax,\xmax) -- (-\xmax,\xmax) -- (\xmax,-\xmax) -- (-\xmax,-\xmax) -- cycle;
\node[mydarkblue,right,align=center] at (-\xmax,0.18*\xmax)
{\contour{myblue!5}{spacelike}\\[-2]\contour{myblue!5}{region}};
\node[mydarkblue,left,align=center] at (\xmax,0.18*\xmax)
{\contour{myblue!5}{spacelike}\\[-2]\contour{myblue!5}{region}};
\node[mydarkorange,align=center] at (-0.22*\xmax,0.67*\xmax)
{\contour{myorange!5}{timelike}\\[-2]\contour{myorange!5}{region}};
\node[mydarkorange,align=center] at (0.22*\xmax,-0.67*\xmax)
{\contour{myorange!5}{timelike}\\[-2]\contour{myorange!5}{region}};
% PHOTON
\draw[photon] ( \xmax,-\xmax) -- ( 0.02*\xmax,-0.02*\xmax);
\draw[photon] (-\xmax,-\xmax) -- (-0.02*\xmax,-0.02*\xmax);
\draw[photon] ( 0.02*\xmax,0.02*\xmax) -- ( \xmax,\xmax)
node[mydarkorange,above right] {$x=ct$};
\draw[photon] (-0.02*\xmax,0.02*\xmax) -- (-\xmax,\xmax);
% PARTICLE WORLDLINE
\draw[particle,decoration={markings,mark=at position 0.27 with {\arrow{latex}},
mark=at position 0.76 with {\arrow{latex}}},postaction={decorate}]
(-0.5*\xmax,-\xmax) to[out=80,in=-110] (O) to[out=70,in=-100] (0.45*\xmax,\xmax);
\fill[mydarkgreen] (O) circle(0.04); % event
\end{tikzpicture}
% SPACETIME DIAGRAM - VECTORS
\begin{tikzpicture}[scale=1.8]
\message{Vectors^^J}
\def\xmax{2}
\def\xmaxp{2.2} % maximum of rotated axis
\def\Nlines{5} % number of world lines (at constant x/t)
\pgfmathsetmacro\d{0.9*\xmax/\Nlines} % grid size
\pgfmathsetmacro\ang{atan(1/3)} % angle between x and x' axes
\coordinate (O) at (0,0);
\coordinate (X) at (\xmax+0.2,0);
\coordinate (T) at (0,\xmax+0.2);
% WORLD LINE GRID
\message{ Making world lines...^^J}
\foreach \i [evaluate={\x=\i*\d;}] in {1,...,\Nlines}{
\message{ Running i/N=\i/\Nlines, x=\x...^^J}
\draw[world line] (-\x,-\xmax) -- (-\x,\xmax);
\draw[world line] ( \x,-\xmax) -- ( \x,\xmax);
\draw[world line t] (-\xmax,-\x) -- (\xmax,-\x);
\draw[world line t] (-\xmax, \x) -- (\xmax, \x);
}
% FILLS
\fill[myblue,opacity=0.05] % SPACELIKE
(\xmax,\xmax) -- (-\xmax,-\xmax) -- (-\xmax,\xmax) -- (\xmax,-\xmax) -- cycle;
\fill[mygreen,opacity=0.05] % TIMELIKE
(\xmax,\xmax) -- (-\xmax,\xmax) -- (\xmax,-\xmax) -- (-\xmax,-\xmax) -- cycle;
% AXES
\draw[->,thick] (0,-\xmax) -- (T) node[left=-1] {$ct$};
\draw[->,thick] (-\xmax,0) -- (X) node[below=0] {$x$};
% VECTORS
\draw[vector,mygreen] (O) --++ (68:0.79*\xmax)
node[right=4,above=-1,align=center]
{\contour{mygreen!5}{timelike vector}\\[-1]
\contour{mygreen!5}{$s^2=c^2t^2-x^2>0$}};
\draw[vector,myblue] (O) --++ (28:0.63*\xmax)
node[below=7,right=-22,align=center]
{\contour{myblue!5}{spacelike}\\[-2]
\contour{myblue!5}{vector}\\[-1]
\contour{myblue!5}{$s^2=c^2t^2-x^2<0$}};
\draw[vector,mygreen,<->] (-2*\d,-\d) --++ (-2*\d,3.5*\d)
node[pos=0.8,below left=-2,align=right]
{\contour{myblue!5}{timelike}\\[-2]
\contour{myblue!5}{separation}\\[-1]
\contour{myblue!5}{$\Delta s^2>0$}};
\draw[vector,myblue,<->] (2*\d,-\d) --++ (3*\d,-2*\d)
node[pos=0.4,above right=-2,align=left]
{\contour{myblue!5}{spacelike}\\[-2]
\contour{myblue!5}{separation}\\[-1]
\contour{myblue!5}{$\Delta s^2<0$}};
\draw[vector,myorange,<->] (2*\d,-3*\d) --++ (2*\d,-2*\d)
node[pos=0.45,below left=-4,align=center]
{\contour{mygreen!5}{lightlike}\\[-2]
\contour{mygreen!5}{separation}\\[-1]
\contour{mygreen!5}{$\Delta s^2 = 0$}};
% PHOTON
\draw[photon] ( \xmax,-\xmax) -- ( 0.02*\xmax,-0.02*\xmax);
\draw[photon] (-\xmax,-\xmax) -- (-0.02*\xmax,-0.02*\xmax);
\draw[photon] ( 0.02*\xmax,0.02*\xmax) -- ( \xmax,\xmax)
node[mydarkorange,above=-1,align=center] {lightlike vector\\[-2]$s^2=c^2t^2+x^2=0$};
\draw[photon] (-0.02*\xmax,0.02*\xmax) -- (-\xmax,\xmax);
\end{tikzpicture}
% SPACETIME DIAGRAM - OVERLAPPING LIGHT CONES
\begin{tikzpicture}[scale=1.8]
\message{Overlapping light cones^^J}
\def\xmax{2}
\def\ext{4*\d} % extension x axis
\def\xmaxp{2.2} % maximum of rotated axis
\def\Nlines{5} % number of world lines (at constant x/t)
\pgfmathsetmacro\d{0.9*\xmax/\Nlines} % grid size
\pgfmathsetmacro\ang{atan(1/3)} % angle between x and x' axes
\coordinate (O) at (0,0);
\coordinate (X) at (\xmax+\ext+0.2,0);
\coordinate (T) at (0,\xmax+0.2);
\coordinate (B) at (4*\d,0); % event B
% WORLD LINE GRID
\message{ Making world lines...^^J}
\foreach \i [evaluate={\x=\i*\d;}] in {1,...,\Nlines}{
\message{ Running i/N=\i/\Nlines, x=\x...^^J}
\draw[world line] (-\x,-\xmax) -- (-\x,\xmax);
\draw[world line] ( \x,-\xmax) -- ( \x,\xmax);
\draw[world line t] (-\xmax,-\x) -- (\xmax+\ext,-\x);
\draw[world line t] (-\xmax, \x) -- (\xmax+\ext, \x);
}
\foreach \i [evaluate={\x=(\Nlines+\i)*\d;}] in {1,...,4}{
\message{ Running i/N=\i/\Nlines, x=\x...^^J}
\draw[world line] (\x,-\xmax) -- ( \x,\xmax);
}
% AXES
\draw[->,thick] (0,-\xmax) -- (T) node[left=-1] {${\color{mydarkred}ct'}=ct$};
\draw[->,thick] (-\xmax,0) -- (X) node[below=0] {$x$};
% LIGHT CONES
\begin{scope}[shift={(B)}]
\fill[myorange!70!red,opacity=0.09]
(0,0) -- (\xmax,\xmax) -- (-\xmax,\xmax) -- (\xmax,-\xmax) -- (-\xmax,-\xmax) -- cycle;
\end{scope}
\fill[myorange!70!green,opacity=0.09]
(O) -- (\xmax,\xmax) -- (-\xmax,\xmax) -- (\xmax,-\xmax) -- (-\xmax,-\xmax) -- cycle;
% PHOTONS
\draw[photon] (135:0.1) -- (135:0.4*\xmax);
\draw[photon] (45:0.1) -- (45:0.4*\xmax);
\draw[photon] (B)++(135:0.1) --++ (135:0.4*\xmax);
\draw[photon] (B)++(45:0.1) --++ (45:0.4*\xmax);
%\draw[photon] (0.05,0.05) -- ( \xmax,\xmax)
% node[mydarkorange,above right] {$x=ct$};
% PARTICLE WORLDLINES
\draw[particle,decoration={markings,mark=at position 0.27 with {\arrow{latex}},
mark=at position 0.76 with {\arrow{latex}}},postaction={decorate}]
(-0.5*\xmax,-\xmax) to[out=80,in=-110] (O) to[out=70,in=-100] (0.45*\xmax,\xmax);
\draw[particle,myred,decoration={markings,mark=at position 0.27 with {\arrow{latex}},
mark=at position 0.74 with {\arrow{latex}}},postaction={decorate}]
(0.84*\xmax,-\xmax) to[out=95,in=-80] (B) to[out=100,in=-76] (0.49*\xmax,\xmax);
% EVENTS
\fill[mydarkgreen] (O) circle(0.04); % event A
\fill[mydarkred] (B) circle(0.04); % event B
\end{tikzpicture}
% SPACETIME DIAGRAM - OVERLAPPING LIGHT CONES with boosted frame
\begin{tikzpicture}[scale=1.8]
\message{Lorentz boost^^J}
\def\xmax{2}
\def\xmaxp{2.2} % maximum of rotated axis
\def\ext{4*\d} % extension x axis
\def\Nlines{5} % number of world lines (at constant x/t)
\pgfmathsetmacro\ang{atan(1/4)} % angle between x and x' axes
\pgfmathsetmacro\d{0.9*\xmax/\Nlines} % grid size
\pgfmathsetmacro\D{\d/cos(\ang)/sqrt(1-tan(\ang)^2)} % grid size, boosted
\coordinate (O) at (0,0);
\coordinate (X) at (\xmax+\ext+0.2,0);
\coordinate (T) at (0,\xmax+0.2);
\coordinate (X') at (\ang:\xmaxp+0.2);
\coordinate (T') at (90-\ang:\xmaxp+0.2);
\coordinate (B) at ($(\ang:3*\D)+(90-\ang:1*\D)$); % event
% WORLD LINE GRID
\message{ Making world lines...^^J}
\foreach \i [evaluate={\x=\i*\d;}] in {1,...,\Nlines}{
\message{ Running i/N=\i/\Nlines, x=\x...^^J}
\draw[world line] (-\x,-\xmax) -- (-\x,\xmax);
\draw[world line] ( \x,-\xmax) -- ( \x,\xmax);
\draw[world line t] (-\xmax,-\x) -- (\xmax+\ext,-\x);
\draw[world line t] (-\xmax, \x) -- (\xmax+\ext, \x);
}
\foreach \i [evaluate={\x=(\Nlines+\i)*\d;}] in {1,...,4}{
\message{ Running i/N=\i/\Nlines, x=\x...^^J}
\draw[world line] (\x,-\xmax) -- ( \x,\xmax);
}
% BOOSTED WORLD LINE GRID
\message{ Making world lines for boosted frame...^^J}
\fill[mydarkred,opacity=0.05]
(O) --++ (\ang:\xmaxp) --++ (90-\ang:\xmaxp) --++ (\ang:-\xmaxp) -- cycle;
\fill[mydarkred,opacity=0.05]
(O) --++ (\ang:-\xmaxp) --++ (90-\ang:-\xmaxp) --++ (\ang:\xmaxp) -- cycle;
\foreach \i [evaluate={\x=\i*\D;}] in {1,...,\Nlines}{
\message{ Running i/N=\i/\Nlines, x=\x...^^J}
\draw[world line'] (\ang:-\x) --++ (90-\ang:-\xmaxp);
\draw[world line'] (90-\ang:-\x) --++ (\ang:-\xmaxp);
\draw[world line'] (\ang:\x) --++ (90-\ang:\xmaxp);
\draw[world line'] (90-\ang:\x) --++ (\ang:\xmaxp);
}
% LIGHT CONES
\begin{scope}
\clip (-\xmax,-\xmax) rectangle (\xmax+\ext,\xmax);
\fill[myorange!70!red,opacity=0.09,shift={(B)}]
(0,0) -- (\xmax,\xmax) -- (-\xmax,\xmax) -- (2*\xmax,-2*\xmax) -- (-2*\xmax,-2*\xmax) -- cycle;
\end{scope}
\fill[myorange!70!green,opacity=0.09]
(O) -- (\xmax,\xmax) -- (-\xmax,\xmax) -- (\xmax,-\xmax) -- (-\xmax,-\xmax) -- cycle;
% PHOTONS
\draw[photon] (135:0.12) -- (135:0.4*\xmax);
\draw[photon] (45:0.12) -- (45:0.4*\xmax);
\draw[photon] (B)++(135:0.12) --++ (135:0.4*\xmax);
\draw[photon] (B)++(45:0.12) --++ (45:0.4*\xmax);
% AXES
\draw[->,thick] (0,-\xmax) -- (T) node[left=-1] {$ct$};
\draw[->,thick] (-\xmax,0) -- (X) node[below=0] {$x$};
\draw[->,thick,mydarkred] (90-\ang:-\xmaxp) -- (T')
node[right=5,above=-1] {$ct' = \gamma\left(ct-\beta x\right)$};
\draw[->,thick,mydarkred] (\ang:-\xmaxp) -- (X') node[right=-1] {$x' = \gamma(x-vt)$};
% EVENTS
\fill[mydarkgreen] (O) circle(0.05); % event A
\fill[mydarkred] (B) circle(0.05); % event B
\end{tikzpicture}
% SPACETIME DIAGRAM - EUCLIDEAN ROTATION
\begin{tikzpicture}[scale=1.8]
\message{Rotation^^J}
\def\xmax{2}
\def\xmaxp{2.1} % maximum of rotated axis
\def\Nlines{5} % number of world lines (at constant x/t)
\pgfmathsetmacro\ang{20} % angle between x and x' axes
\pgfmathsetmacro\d{0.9*\xmax/\Nlines} % grid size
\coordinate (O) at (0,0);
\coordinate (X) at (\xmax+0.2,0);
\coordinate (T) at (0,{(1+0.5*sin(\ang))*\xmax+0.2});
\coordinate (X') at (\ang:\xmaxp+0.2);
\coordinate (T') at (90+\ang:\xmaxp+0.2);
% WORLD LINE GRID
\message{ Making world lines...^^J}
\foreach \i [evaluate={\x=\i*\d;}] in {1,...,\Nlines}{
\message{ Running i/N=\i/\Nlines, x=\x...^^J}
\draw[world line] (-\x,-\xmax) -- (-\x,\xmax);
\draw[world line] ( \x,-\xmax) -- ( \x,\xmax);
\draw[world line t] (-\xmax,-\x) -- (\xmax,-\x);
\draw[world line t] (-\xmax, \x) -- (\xmax, \x);
}
% BOOSTED WORLD LINE GRID
\message{ Making world lines for boosted frame...^^J}
\fill[mydarkred,opacity=0.05]
(O) --++ (\ang:\xmaxp) --++ (90+\ang:\xmaxp) --++ (\ang:-\xmaxp) -- cycle;
\fill[mydarkred,opacity=0.05]
(O) --++ (\ang:-\xmaxp) --++ (90+\ang:-\xmaxp) --++ (\ang:\xmaxp) -- cycle;
\foreach \i [evaluate={\x=\i*\d;}] in {1,...,\Nlines}{
\message{ Running i/N=\i/\Nlines, x=\x...^^J}
\draw[world line'] (\ang:-\x) --++ (90+\ang:-\xmaxp);
\draw[world line'] (90+\ang:-\x) --++ (\ang:-\xmaxp);
\draw[world line'] (\ang:\x) --++ (90+\ang:\xmaxp);
\draw[world line'] (90+\ang:\x) --++ (\ang:\xmaxp);
}
% AXES
\draw[->,thick] (0,-\xmax) -- (T) node[left=-1] {$y$};
\draw[->,thick] (-\xmax,0) -- (X) node[below=0] {$x$};
\draw[->,thick,mydarkred] (90+\ang:-\xmaxp) -- (T')
node[left=13,above=-1] {$y'=\cos\theta\,y-\sin\theta\,x$};
\draw[->,thick,mydarkred] (\ang:-\xmaxp) -- (X')
node[above=7,right=-11] {$x'=\cos\theta\,x+\sin\theta\,y$};
% ANGLES
\draw pic[->,"$\theta$",draw=black,angle radius=34,angle eccentricity=1.2] {angle = X--O--X'};
\draw pic[->,"$\theta$",draw=black,angle radius=35,angle eccentricity=1.2] {angle = T--O--T'};
\end{tikzpicture}
% SPACETIME DIAGRAM - GALILEAN TRANSFORMATION
\begin{tikzpicture}[scale=1.8]
\message{Galilean transformation^^J}
\def\xmax{2}
\def\xmaxp{2.1} % maximum of rotated axis
\def\Nlines{4} % number of world lines (at constant x/t)
\pgfmathsetmacro\d{0.9*\xmax/\Nlines} % grid size
\pgfmathsetmacro\ang{atan(1/3)} % angle
\coordinate (O) at (0,0);
\coordinate (X) at (\xmax+0.2,0);
\coordinate (T) at (0,\xmax+0.2);
\coordinate (X') at (\ang:\xmaxp+0.2);
\coordinate (T') at (90-\ang:\xmaxp+0.2);
% WORLD LINES GRID
\message{ Making world lines...^^J}
\foreach \i [evaluate={\x=\i*\d;}] in {1,...,\Nlines}{
\message{ Running i/N=\i/\Nlines, x=\x...^^J}
\draw[world line] (-\x,-\xmax) -- (-\x,\xmax);
\draw[world line] ( \x,-\xmax) -- ( \x,\xmax);
\draw[world line t] ({-\xmax-tan(\ang)*\x},-\x) -- (\xmax,-\x);
\draw[world line t] (-\xmax,\x) -- ({\xmax+tan(\ang)*\x},\x);
}
% AXES
\draw[->,thick] (0,-\xmax) -- (T) node[left=0] {$ct$};
\draw[->,thick] (-\xmax,0) -- (X) node[right=6,below=-1] {$x={\color{mydarkred}x'}$};
\draw[->,thick,mydarkred] (90-\ang:-\xmaxp) -- (T')
node[left=-1] {$ct'$}
node[right=2,below right=-2] {$x = vt$};
% WORLD LINES GRID - BOOSTED
\message{ Making world lines, boosted...^^J}
\fill[mydarkred,opacity=0.05]
(O) --++ (90-\ang:\xmax) --++ (\xmax,0) --++ (90-\ang:-\xmax) -- cycle;
\fill[mydarkred,opacity=0.05]
(O) --++ (90-\ang:-\xmax) --++ (-\xmax,0) --++ (90-\ang:\xmax) -- cycle;
\foreach \i [evaluate={\x=\i*\d;}] in {1,...,\Nlines}{
\message{ Running i/N=\i/\Nlines, x=\x...^^J}
\draw[world line'] (\x,0) --++ (90-\ang:\xmax);
\draw[world line'] (-\x,0) --++ (90-\ang:-\xmax);
}
\draw pic[<-,"$\theta$",draw=black,angle radius=34,angle eccentricity=1.2] {angle = T'--O--T};
\end{tikzpicture}
% SPACETIME DIAGRAM - LORENTZ BOOST
\begin{tikzpicture}[scale=1.8]
\message{Lorentz boost^^J}
\def\xmax{2}
\def\xmaxp{2.2} % maximum of rotated axis
\def\Nlines{5} % number of world lines (at constant x/t)
\pgfmathsetmacro\ang{atan(1/3)} % angle between x and x' axes
\pgfmathsetmacro\d{0.9*\xmax/\Nlines} % grid size
\pgfmathsetmacro\D{\d/cos(\ang)/sqrt(1-tan(\ang)^2)} % grid size, boosted
\coordinate (O) at (0,0);
\coordinate (X) at (\xmax+0.2,0);
\coordinate (T) at (0,\xmax+0.2);
\coordinate (X') at (\ang:\xmaxp+0.2);
\coordinate (T') at (90-\ang:\xmaxp+0.2);
% WORLD LINE GRID
\message{ Making world lines...^^J}
\foreach \i [evaluate={\x=\i*\d;}] in {1,...,\Nlines}{
\message{ Running i/N=\i/\Nlines, x=\x...^^J}
\draw[world line] (-\x,-\xmax) -- (-\x,\xmax);
\draw[world line] ( \x,-\xmax) -- ( \x,\xmax);
\draw[world line t] (-\xmax,-\x) -- (\xmax,-\x);
\draw[world line t] (-\xmax, \x) -- (\xmax, \x);
}
% BOOSTED WORLD LINE GRID
\message{ Making world lines for boosted frame...^^J}
\fill[mydarkred,opacity=0.05]
(O) --++ (\ang:\xmaxp) --++ (90-\ang:\xmaxp) --++ (\ang:-\xmaxp) -- cycle;
\fill[mydarkred,opacity=0.05]
(O) --++ (\ang:-\xmaxp) --++ (90-\ang:-\xmaxp) --++ (\ang:\xmaxp) -- cycle;
\foreach \i [evaluate={\x=\i*\D;}] in {1,...,\Nlines}{
\message{ Running i/N=\i/\Nlines, x=\x...^^J}
\draw[world line'] (\ang:-\x) --++ (90-\ang:-\xmaxp);
\draw[world line'] (90-\ang:-\x) --++ (\ang:-\xmaxp);
\draw[world line'] (\ang:\x) --++ (90-\ang:\xmaxp);
\draw[world line'] (90-\ang:\x) --++ (\ang:\xmaxp);
}
% AXES
\draw[->,thick] (0,-\xmax) -- (T) node[left=-1] {$ct$};
\draw[->,thick] (-\xmax,0) -- (X) node[below=0] {$x$};
\draw[->,thick,mydarkred] (90-\ang:-\xmaxp) -- (T')
node[right=5,above=-1] {$ct' = \gamma\left(ct-\beta x\right)$};
\draw[->,thick,mydarkred] (\ang:-\xmaxp) -- (X') node[right=-1] {$x' = \gamma(x-vt)$};
% ANGLES
\draw pic[->,"$\theta$",draw=black,angle radius=34,angle eccentricity=1.2] {angle = X--O--X'};
\draw pic[<-,"$\theta$",draw=black,angle radius=34,angle eccentricity=1.2] {angle = T'--O--T};
% PHOTON
\draw[photon] (0.32*\xmax,0.32*\xmax) --++ (45:0.4*\xmax);
\end{tikzpicture}
% SPACETIME DIAGRAM - INVERSE LORENTZ BOOST
\begin{tikzpicture}[scale=1.8]
\message{Inverse Lorentz boost^^J}
\def\xmax{2}
\def\xmaxp{2.2} % maximum of rotated axis
\def\Nlines{5} % number of world lines (at constant x/t)
\pgfmathsetmacro\ang{atan(-1/3)} % inverted angle
\pgfmathsetmacro\d{0.9*\xmax/\Nlines} % grid size
\pgfmathsetmacro\D{\d/cos(\ang)/sqrt(1-tan(\ang)^2)} % grid size, boosted
\coordinate (O) at (0,0);
\coordinate (X) at (\xmax+0.2,0);
\coordinate (T) at (0,\xmax+0.2);
\coordinate (X') at (\ang:\xmaxp+0.2);
\coordinate (T') at (90-\ang:\xmaxp+0.2);
% WORLD LINE GRID
\message{ Making world lines...^^J}
\foreach \i [evaluate={\x=\i*\d;}] in {1,...,\Nlines}{
\message{ Running i/N=\i/\Nlines, x=\x...^^J}
\draw[world line] (-\x,-\xmax) -- (-\x,\xmax);
\draw[world line] ( \x,-\xmax) -- ( \x,\xmax);
\draw[world line t] (-\xmax,-\x) -- (\xmax,-\x);
\draw[world line t] (-\xmax, \x) -- (\xmax, \x);
}
% BOOSTED WORLD LINE GRID
\message{ Making world lines for boosted frame...^^J}
\fill[mydarkred,opacity=0.05]
(O) --++ (\ang:\xmaxp) --++ (90-\ang:\xmaxp) --++ (\ang:-\xmaxp) -- cycle;
\fill[mydarkred,opacity=0.05]
(O) --++ (\ang:-\xmaxp) --++ (90-\ang:-\xmaxp) --++ (\ang:\xmaxp) -- cycle;
\foreach \i [evaluate={\x=\i*\D;}] in {1,...,\Nlines}{
\message{ Running i/N=\i/\Nlines, x=\x...^^J}
\draw[world line'] (\ang:-\x) --++ (90-\ang:-\xmaxp);
\draw[world line'] (90-\ang:-\x) --++ (\ang:-\xmaxp);
\draw[world line'] (\ang:\x) --++ (90-\ang:\xmaxp);
\draw[world line'] (90-\ang:\x) --++ (\ang:\xmaxp);
}
% AXES
\draw[->,thick] (0,-\xmax) -- (T) node[left=-1] {$ct$};
\draw[->,thick] (-\xmax,0) -- (X) node[below=0] {$x$};
\draw[->,thick,mydarkred] (90-\ang:-\xmaxp) -- (T')
node[right=5,above=-1] {$ct' = \gamma\left(ct+\beta x\right)$};
\draw[->,thick,mydarkred] (\ang:-\xmaxp) -- (X') node[right=-1] {$x' = \gamma(x+vt)$};
% ANGLES
\draw pic[<-,"\contour{myfieldred}{$\theta$}",draw=black,angle radius=33,angle eccentricity=1.2] {angle = X'--O--X};
\draw pic[->,"\contour{myfieldred}{$\theta$}",draw=black,angle radius=33,angle eccentricity=1.2] {angle = T--O--T'};
% PHOTON
\draw[photon] (0.32*\xmax,0.32*\xmax) --++ (45:0.4*\xmax);
\end{tikzpicture}
% COMMON AXES
\pgfdeclarelayer{back} % to draw on background
\pgfsetlayers{back,main} % set order
\def\xmin{0.23}
\def\xmax{2}
\def\Nlines{6} % number of world lines (at constant x/t)
\def\DNxp{0} % difference in number of world lines of x' axis
\def\DNyp{0} % difference in number of world lines of ct' axis
\def\DNy{0} % difference in number of world lines of ct axis
\def\ang{20} % angle between x and x' axes
\def\xplabelang{180} % anchor angle of x' axis label
%\pgfmathsetmacro\ang{atan(0.44)} % angle between x and x' axes
\def\axes{
\pgfmathsetmacro\d{\xmax/(\Nlines+0.4)} % grid size
\pgfmathsetmacro\D{\d/cos(\ang)/sqrt(1-tan(\ang)^2)} % grid size, boosted
\pgfmathsetmacro\ymax{\xmax+\DNy*\d} % maximum of y = ct axis
\pgfmathsetmacro\xmaxp{(\xmax/\d+\DNxp)*\D} % maximum of x' axis
\pgfmathsetmacro\ymaxp{(\xmax/\d+\DNyp)*\D} % maximum of y' = ct' axis
\pgfmathsetmacro\Nylines{\Nlines+\DNy} % number of world lines at constant ct'
\pgfmathsetmacro\Nxplines{\Nlines+\DNxp} % number of world lines at constant x'
\pgfmathsetmacro\Nyplines{\Nlines+\DNyp} % number of world lines at constant ct'
\coordinate (O) at (0,0);
\coordinate (X) at (\xmax+0.15,0);
\coordinate (T) at (0,\ymax+0.15);
\coordinate (X') at (\ang:\xmaxp+0.2);
\coordinate (T') at (90-\ang:\ymaxp+0.2);
% FILL
\begin{pgfonlayer}{back} % draw on back
\fill[myfieldred]
(\ang:-\xmin) -- (\ang:\xmaxp) --++ (90-\ang:\ymaxp) --++ (\ang:-\xmaxp)
-- (90-\ang:-\xmin) -- cycle;
\end{pgfonlayer}
% WORLD LINE GRID
\message{ Making world lines...^^J}
\foreach \i [evaluate={\x=\i*\d;}] in {1,...,\Nlines}{
%\message{ Running i/N=\i/\Nlines, x=\x...^^J}
\draw[world line] (\x,0) -- (\x,\ymax);
}
\foreach \i [evaluate={\t=\i*\d;}] in {1,...,\Nylines}{
%\message{ Running i/N=\i/\Nlines, t=\t...^^J}
\draw[world line t] (0,\t) -- (\xmax,\t);
}
% BOOSTED WORLD LINE GRID
\message{ Making world lines for boosted frame...^^J}
\foreach \i [evaluate={\x=\i*\D;}] in {1,...,\Nxplines}{
%\message{ Running i/N=\i/\Nlines, x=\x...^^J}
\draw[world line'] (\ang:\x) --++ (90-\ang:\ymaxp);
}
\foreach \i [evaluate={\t=\i*\D;}] in {1,...,\Nyplines}{
%\message{ Running i/N=\i/\Nlines, t=\t...^^J}
\draw[world line'] (90-\ang:\t) --++ (\ang:\xmaxp);
}
% AXES
\draw[->,thick] (0,-\xmin) -- (T) node[left=-1] {$ct$};
\draw[->,thick] (-\xmin,0) -- (X) node[below=0] {$x$};
\draw[->,thick,mydarkred] (90-\ang:-\xmin) -- (T')
node[right=5,above=-1] {$ct'$};
\draw[->,thick,mydarkred] (\ang:-\xmin) -- (X')
node[anchor=\xplabelang,inner sep=2] {$x'$};
}
% SPACETIME DIAGRAM - SIMULTANEITY (in S)
\begin{tikzpicture}[scale=1.8]
\message{Simultaneity^^J}
% AXES
\axes
% SETTINGS
\def\L{0.91*\xmaxp} % length of the dashed lines
\pgfmathsetmacro\xA{2*\d} % x coordinate of A in S
\pgfmathsetmacro\yA{4*\d} % x coordinate of A in S
\pgfmathsetmacro\dx{4*\d} % time difference in S
\pgfmathsetmacro\xAp{(\xA-tan(\ang)*\yA)/cos(\ang)^2/sqrt(1-tan(\ang)^2)} % x coordinate of A in S'
\pgfmathsetmacro\dtp{4*\d*sin(\ang)/cos(2*\ang)} % time difference between A and B in S'
\coordinate (A) at (\xA,\yA);
\coordinate (B) at (\xA+\dx,\yA);
\coordinate (A') at ($(A)-(\ang:0.11*\xmaxp)$); % left side of dashed line through A
\coordinate (B') at ($(A')-(90-\ang:\dtp)$); % left side of dashed line through B
% FILL
\begin{pgfonlayer}{back} % draw on back
\fill[mylightred]
%(A') -- (B') -- ($(B)+(\ang:0.07)$) --++ (90-\ang:\dtp) -- cycle;
(A)++(\ang:-\xAp) --++ (90-\ang:-\dtp) -- ($(B)+(\ang:0.07)$) --++ (90-\ang:\dtp) -- cycle;
\draw[mylightblue2,line width=1.8] (0,\yA) -- (B);
\end{pgfonlayer}
% EVENTS
%\draw[mygreen,thick] (A) -- (B);
\draw[mygreen,mydashed,thin]
(A') --++ (\ang:\L);
\draw[myblue,mydashed,thin]
(B') --++ (\ang:\L);
\fill[mydarkgreen] (A) circle(0.04) % event A
node[above=0] {\contour{myfieldred}{A}};
\fill[mydarkblue] (B) circle(0.04) % event B
node[above left=-1] {\contour{mylightred}{B}};
% ARROW
\draw[mysmallarr,mydarkred] (B)++(\ang:0.13) --++ (90-\ang:\dtp)
node[pos=0.55,right=-2] {\contour{myfieldred}{$c\Delta t'$}};
\end{tikzpicture}
% SPACETIME DIAGRAM - SIMULTANEITY (in S')
\begin{tikzpicture}[scale=1.8]
\message{Simultaneity^^J}
% AXES
\axes
% EVENTS
\def\L{1.1*\xmaxp}
\coordinate (A) at (90-\ang:3*\D);
\coordinate (B) at ($(\ang:5*\D)+(90-\ang:3*\D)$);
%\draw[mygreen,thick] (A) -- (B);
\draw[mygreen,mydashed,thin]
(A)++(-0.23*\xmaxp,0) --++ (\L,0);
\draw[myblue,mydashed,thin]
(B)++(-0.964*\xmaxp,0) --++ (\L,0);
\fill[mydarkgreen] (A) circle(0.04) % event A
node[anchor=-55,inner sep=3] {\contour{mylightblue2}{A}};
\fill[mydarkblue] (B) circle(0.04) % event B
node[above left=-1] {\contour{myfieldred}{B}};
% HIGHLIGHT
\begin{pgfonlayer}{back} % draw on back
\fill[mylightblue2]
($(O)!(A)!(T)$) rectangle ($(B)+(0.06,0)$);
\draw[mylightred,line width=1.8] (A) -- (B);
\end{pgfonlayer}
% ARROW
\pgfmathsetmacro\dt{5*\D*sin(\ang)} % time difference between A and B in S
\draw[mysmallarr] (A)++(0.81*\xmaxp,0) --++ (0,\dt)
node[pos=0.5,right=-2] {$c\Delta t$};
\end{tikzpicture}
% SPACETIME DIAGRAM - SIMULTANEITY (different order)
\begin{tikzpicture}[scale=1.8]
\message{Simultaneity^^J}
% AXES
\def\ang{19.27} % angle between x and x' axes
\axes
% SETTINGS
\pgfmathsetmacro\tA{3*\D*cos(\ang)} % time coordinate of A in S
\coordinate (A) at (90-\ang:3*\D);
\coordinate (B) at ($(\ang:5*\D)+(90-\ang:2*\D)$);
% FILL
\begin{pgfonlayer}{back} % draw on back
\fill[mylightblue2]
($(O)!(A)!(T)$) rectangle ($(B)+(0.07,0)$);
\fill[mylightred]
(A) --++ (\ang:5*\D) --++ (90-\ang:-\D) --++ (\ang:-5*\D) -- cycle;
\end{pgfonlayer}
% EVENTS
\draw[mygreen,mydashed,thin]
(A)++(-0.22*\xmaxp,0) --++ (1.08*\xmaxp,0) coordinate(A');
\draw[myblue,mydashed,thin]
(B)++(-0.906*\xmaxp,0) --++ (1.08*\xmaxp,0);
\fill[mydarkgreen] (A) circle(0.04) % event A
node[anchor=-55,inner sep=3] {\contour{mylightblue2}{A}};
\fill[mydarkblue] (B) circle(0.04) % event B
node[above left=-2] {B};
% ARROWS
\draw[mysmallarr,mydarkred] (B)++(\ang:0.09) --++ (90-\ang:\D)
node[pos=0.55,right=-2.5] {\contour{myfieldred}{$c\Delta t$}$'>0$};
\draw[mysmallarr] (B)++(0.1,0) --++ ($(0,\tA)-($(O)!(B)!(0,\xmax)$)$)
node[pos=0.45,right=-2] {\contour{myfieldred}{$c\Delta$}$t<0$};
\end{tikzpicture}
% SPACETIME DIAGRAM - TIME DILATION of space point fixed in S
% Inspiration: http://people.uncw.edu/hermanr/GR/Minkowski/Minkowski.pdf
\begin{tikzpicture}[scale=1.8]
\message{Time dialation (fixed space point in S)^^J}
% AXES
\axes
% SETTINGS
\pgfmathsetmacro\dt{5*\d} % time difference in S
\pgfmathsetmacro\dtp{\dt*cos(\ang)/cos(2*\ang)} % time difference in S'
\pgfmathsetmacro\dxp{\dt*sin(\ang)/cos(2*\ang)} % distance in S'
\pgfmathsetmacro\xBp{(-tan(\ang)*\dt)/cos(\ang)^2/sqrt(1-tan(\ang)^2)} % x coordinate of A in S'
\coordinate (A) at (0,0);
\coordinate (B) at (0,\dt);
\coordinate (C) at ($(B)+(\ang:\dxp)$);
% FILL
\begin{pgfonlayer}{back} % draw on back
\fill[mylightred] (A) -- (B) -- (C) -- cycle;
\end{pgfonlayer}
% TRIANGLE
\draw[very thick,myred,rounded corners=0.1]
(A) -- (C) node[midway,right=-2] {\contour{myfieldred}{$c\Delta t'$}}
-- (B) node[midway,above=0] {\contour{white}{$\Delta x'$}}
-- cycle node[pos=0.5,left=-2] {$c\Delta t$};
\fill[mydarkred] (A) circle(0.03) node[above left=0] {A};
\fill[mydarkred] (B) circle(0.03) node[below=1,left=0] {B};
\fill[mydarkred] (C) circle(0.03) node[below=0,right=0] {\contour{myfieldred}{B$'$}};
\end{tikzpicture}
% SPACETIME DIAGRAM - TIME DILATION of space point fixed in S (alternative derivation)
% Inspiration: http://people.uncw.edu/hermanr/GR/Minkowski/Minkowski.pdf
\begin{tikzpicture}[scale=1.8]
\message{Time dialation (fixed space point in S)^^J}
% AXES
\axes
% SETTINGS
\pgfmathsetmacro\xA{4*\d} % x coordinate of A in S
\pgfmathsetmacro\yA{3*\d} % x coordinate of A in S
\pgfmathsetmacro\dt{3*\d} % time difference in S
\pgfmathsetmacro\dtp{\dt*cos(\ang)/cos(2*\ang)} % time difference in S'
\pgfmathsetmacro\dxp{\dt*sin(\ang)/cos(2*\ang)} % distance in S'
\pgfmathsetmacro\xBp{(\xA-tan(\ang)*(\yA+\dt))/cos(\ang)^2/sqrt(1-tan(\ang)^2)} % x coordinate of A in S'
\coordinate (A) at (\xA,\yA);
\coordinate (B) at (\xA,\yA+\dt);
\coordinate (C) at ($(A)-(\ang:\dxp)$);
% FILL
\begin{pgfonlayer}{back} % draw on back
\fill[mylightblue2]
($(O)!(A)!(T)$) rectangle (B);
\fill[mylightred]
(B) -- (C) --++ (\ang:-\xBp) --++ (90-\ang:\dtp) -- cycle;
\end{pgfonlayer}
% TRIANGLE
\draw[very thick,myred,rounded corners=0.1]
(A) -- (C) node[midway,below=0] {\contour{myfieldred}{$\Delta x'$}}
-- (B) node[midway,left=-2] {\contour{mylightred}{$c\Delta t'$}}
-- cycle node[pos=0.52,right=-2] {\contour{myfieldred}{$c\Delta t$}};
\fill[mydarkred] (A) circle(0.03) node[below=0,right=0] {\contour{myfieldred}{A}};
\fill[mydarkred] (B) circle(0.03) node[below=1,right=0] {\contour{myfieldred}{B}};
\fill[mydarkred] (C) circle(0.03);
\end{tikzpicture}
% SPACETIME DIAGRAM - TIME DILATION of fixed space point fixed in S'
% Inspiration: http://people.uncw.edu/hermanr/GR/Minkowski/Minkowski.pdf
\begin{tikzpicture}[scale=1.8]
\message{Time dialation (fixed space point in S')^^J}
% AXES
\axes
% SETTINGS
\pgfmathsetmacro\xAp{2*\D} % x coordinate of A in S'
\pgfmathsetmacro\yAp{2*\D} % x coordinate of A in S'
\pgfmathsetmacro\dtp{3*\D} % time difference in S'
\pgfmathsetmacro\dx{\dtp*sin(\ang)} % distance in S'
\coordinate (A) at ($(\ang:\xAp)+(90-\ang:\yAp)$);
\coordinate (B) at ($(A)+(90-\ang:\dtp)$);
\coordinate (C) at ($(A)+(\dx,0)$);
% FILL
\begin{pgfonlayer}{back} % draw on back
\fill[mylightblue2]
($(O)!(A)!(T)$) rectangle (B);
\fill[mylightred]
(A) --++ (\ang:-\xAp) --++ (90-\ang:\dtp) -- (B) -- cycle;
\end{pgfonlayer}
% TRIANGLE
\draw[very thick,myred,rounded corners=0.1]
(A) -- (C) node[midway,below=-1] {\contour{myfieldred}{$\Delta x$}}
-- (B) node[midway,right=-2] {\contour{myfieldred}{$c\Delta t$}}
-- cycle node[pos=0.52,left=-2] {\contour{mylightred}{$c\Delta t'$}};
\fill[mydarkred] (A) circle(0.03) node[below=2,left=-2] {\contour{myfieldred}{A}};
\fill[mydarkred] (B) circle(0.03) node[above=1,left=-1] {\contour{myfieldred}{B}};
\fill[mydarkred] (C) circle(0.03);
\end{tikzpicture}
% SPACETIME DIAGRAM - LENGTH CONTRACTION of rod at rest in S
% Inspiration: http://people.uncw.edu/hermanr/GR/Minkowski/Minkowski.pdf
\def\ang{23} % angle between x and x' axes
\begin{tikzpicture}[scale=1.8]
\message{Length contraction (rod at rest in S)^^J}
% AXES
\def\Nlines{7} % number of world lines (at constant x/t)
\axes
% SETTINGS
\pgfmathsetmacro\xA{2*\d} % triangle left corner x coordinate in S
\pgfmathsetmacro\yA{4*\d} % triangle left corner y=ct coordinate in S
\pgfmathsetmacro\Lz{4*\d} % proper/rest length L0 in S
\pgfmathsetmacro\L{\Lz/cos(\ang)} % length L in S'
\coordinate (L) at (\Lz,0); % rod end in S
\coordinate (L') at (\ang:\L); % rod end in S'
\coordinate (A) at (\xA,\yA); % point A in triangle
\coordinate (B) at (\xA+\Lz,\yA); % point B in triangle
\coordinate (B') at (\xA+\Lz,{\yA+\Lz*tan(\ang)}); % point B' in triangle
% FILL
\begin{pgfonlayer}{back} % draw on back
\fill[mylightblue2] (\xA,-\xmin) rectangle (\xA+\Lz,\xmax);
\end{pgfonlayer}
\draw[->,thick,mydarkbrown] (\xA,-\xmin) --++ (0,\xmin+\xmax+0.2);
\draw[->,thick,mydarkbrown] (\xA+\Lz,-\xmin) --++ (0,\xmin+\xmax+0.2);
% ROD
\draw[rod] (\xA,0) --++ (L)
node[midway,below=-1] {$L_0$};
\draw[rod] (\ang:{\xA/cos(\ang)}) --++ (L')
node[pos=0.485,above=1] {\contour{mylightblue2}{$L$}};
% TRIANGLE
\draw[very thick,myred,rounded corners=0.1]
(A) -- (B') node[midway,above=0] {\contour{mylightblue2}{$\Delta x'$}}
-- (B) node[midway,right=-2] {\contour{myfieldred}{$c\Delta t$}}
-- cycle node[pos=0.51,below=-1] {\contour{mylightblue2}{$\Delta x$}};
%\fill[myfieldred] (A)++(185:0.089) circle(0.04);
%\fill[mydarkred] (A) circle(0.03) node[below=1,left=-2.7] {A};
\fill[myfieldred] (A)++(200:0.1) circle(0.04);
\fill[mydarkred] (A) circle(0.03) node[below=1,left=-2.3] {\contour{myfieldred}{A}};
\fill[mydarkred] (B) circle(0.03) node[below=1,right=0] {\contour{myfieldred}{B}};
\fill[mydarkred] (B') circle(0.03) node[above=2,right=-1] {\contour{myfieldred}{B$'$}};
\end{tikzpicture}
% SPACETIME DIAGRAM - LENGTH CONTRACTION of moving rod (at rest in S')
\begin{tikzpicture}[scale=1.8]
\message{Length contraction (rod at rest in S')^^J}
% AXES
\def\Nlines{6} % number of world lines (at constant x/t)
\axes
% SETTINGS
\pgfmathsetmacro\Lz{4*\D} % proper/rest length L0 in S'
\pgfmathsetmacro\L{cos(2*\ang)/cos(\ang)*\Lz} % contracted length L in S
\coordinate (L) at (\L,0); % rod end in S
\coordinate (L') at (\ang:\Lz); % rod end in S'
\coordinate (A) at (90-\ang:{3*\d/cos(\ang)}); % point A in triangle
\coordinate (B) at ($(A)+(L)$); % point B' in triangle
\coordinate (B') at ($(A)+(L')$); % point B in triangle
% FILL
\begin{pgfonlayer}{back} % draw on back
\fill[mylightred]
(90-\ang:-\xmin) -- (90-\ang:\xmaxp) --++ (\ang:\Lz) -- (L) --++ (90-\ang:-\xmin) -- cycle;
\end{pgfonlayer}
\draw[->,thick,mydarkbrown] (L)++(90-\ang:-\xmin) -- (L) -- (L') --++ (90-\ang:\xmaxp+0.2);
% ROD
\draw[rod] (O) -- (L)
node[midway,below=-1] {$L$};
\draw[rod] (O) -- (L')
node[pos=0.49,above=1] {\contour{mylightred}{$L_0$}};
% TRIANGLE
\draw[very thick,myred,rounded corners=0.1]
(A) -- (B') node[midway,above=0] {\contour{mylightred}{$\Delta x'$}}
-- (B) node[midway,right=-2] {\contour{myfieldred}{$c\Delta t'$}}
-- cycle node[pos=0.525,below=-1] {\contour{mylightred}{$\Delta x$}};
\fill[mydarkred] (A) circle(0.03) node[below=0,left=0] {\contour{white}{A}};
\fill[mydarkred] (B) circle(0.03) node[below=1,right=0] {\contour{myfieldred}{B}};
\fill[mydarkred] (B') circle(0.03) node[below=0.5,right=-1] {\contour{myfieldred}{B$'$}};
\end{tikzpicture}
% SPACETIME DIAGRAM - LADDER PARADOX
\begin{tikzpicture}[scale=2.5]
\message{Ladder paradox^^J}
%\def\R{2*\xmax} % radius of clip
%\clip (-\xmin,\R) |- (\R,-\xmin) arc(0:90:\xmin+\R);
% AXES
\def\xmin{0.2}
\def\xmax{2.6}
\def\ang{33.5} % angle between x and x' axes
\def\Nlines{12} % number of world lines (at constant x/t)
\def\DNy{1} % difference in number of world lines of y axis (lengthen)
\def\DNxp{-6} % difference in number of world lines of x' axis (shorten)
\def\DNyp{-2} % difference in number of world lines of y' axis (shorten)
\def\xplabelang{170} % anchor angle of x' axis label
\axes
% SETTINGS
\pgfmathsetmacro\Lz{4*\D} % proper/rest length L0 of ladder in S'
\pgfmathsetmacro\L{cos(2*\ang)/cos(\ang)*\Lz} % contracted length L in S
\pgfmathsetmacro\yminb{-0.7*\xmin} % ymin of barn in S
\pgfmathsetmacro\xb{4.96*\d} % x coordinate of barn in S
\pgfmathsetmacro\wb{3.08*\d} % width of barn in S
\pgfmathsetmacro\yA{(\xb+0.04*\d)/tan(\ang)} % y = ct coordinate when ladder is fully in barn in S
\coordinate (L) at (\L,0); % ladder end in S
\coordinate (L') at (\ang:\Lz); % ladder end in S'
\coordinate (A) at (90-\ang:{(\xb+0.04*\d)/sin(\ang)}); % left end of ladder when fully in barn
\coordinate (B) at ($(A)+(\L,0)$); % right end of ladder when fully in barn
\coordinate (C) at (90-\ang:{(\xb+\wb+0.08*\d)/sin(\ang)}); % left end of ladder when fully passed through barn
% FILL
\begin{pgfonlayer}{back} % draw on back (behind axes)
\fill[mydarkblue!22] % barn frame
(\xb,\yminb) rectangle (\xb+\wb,\ymax);
\fill[mylightred] % ladder frame
(90-\ang:-\xmin) -- (90-\ang:\ymaxp) --++ (\ang:\Lz) -- (L) --++ (90-\ang:-\xmin) -- cycle;
\begin{scope}
\clip (0,0) rectangle(1.3*\xmax,\ymax+0.2);
\draw[myredhighlight,line width=3.1] % highlight simultaneity in S'
(A)++(\ang:{-\xb/cos(\ang)-0.05}) --++ (\ang:\xmax+3.6*\D)
(B)++(\ang:{-\xb/cos(\ang)-0.05-\Lz}) --++ (\ang:\xmax+3.8*\D);
\draw[mypurplehighlight,line width=3.1] % highlight simultaneity in S
(0,\yA) --++ (\xmax+0.8*\d,0);
\end{scope}
\end{pgfonlayer}
\draw[->,thick,mydarkblue] % barn left door
(\xb,\yminb) -- (\xb,\ymax+0.15);
\draw[->,thick,mydarkblue] % barn right door
(\xb+\wb,\yminb) -- (\xb+\wb,\ymax+0.15);
\draw[->,thick,mydarkbrown] % rod left end
(L)++(90-\ang:-\xmin) -- (L) -- (L') --++ (90-\ang:\ymaxp+0.2);
% LADDER
\draw[rod] (O) -- (L')
node[pos=0.55,above=2,scale=0.8] {\contour{mylightred}{$L_0$}};
\draw[rod] (O) -- (L)
node[pos=0.46,below=1,scale=0.8] {$L$};
% LADDER IN BARN
\draw[rod] (A) --++ (L');
\draw[rod] (B) --++ (\ang:-\Lz);
\draw[rod] (A) --++ (L);
% LADDER RIGHT OF BARN
\draw[rod] (C) --++ (L');
\draw[rod] (C) --++ (L);
% LABELS
\node[mydarkblue,below=0,align=center,scale=0.8,yshift=1] at (\xb+\wb/2,0)
{barn\\$L<w<L_0$};
\node[mydarkpurple,right,align=left,scale=0.65,yshift=1.2] at (\xb+3.6*\d,\yA)
{both doors closed in S};
%{both doors\\[-3]close in S};
\node[mydarkred,right,scale=0.65,yshift=1.8,rotate=\ang] at ($(A)+(\ang:\Lz+0.8*\D)$)
{left door closed in S$'$};
\node[mydarkred,right,scale=0.65,yshift=0.7,rotate=\ang] at ($(B)+(\ang:0.8*\D)$)
{right door closed in S$'$};
\end{tikzpicture}
% SPACETIME DIAGRAM - LADDER PARADOX from perspective of S' (i.e. in the S' frame)
\begin{tikzpicture}[scale=2.5]
\message{Ladder paradox from the perspective of S'^^J}
% SETTINGS
\def\ang{-33.5} % angle between x and x' axes
\def\Nxlines{9} % number of world lines (at constant x)
\def\Nylines{13} % number of world lines (at constant t)
\def\Nxplines{6} % number of world lines (at constant x')
\def\Nyplines{10} % number of world lines (at constant t')
\def\xmin{0.2}
\pgfmathsetmacro\D{2.6/13} % grid size
\pgfmathsetmacro\d{\D/cos(\ang)/sqrt(1-tan(\ang)^2)} % grid size, boosted
\pgfmathsetmacro\xmax{(\Nxlines+0.4)*\d} % maximum of x axis in S
\pgfmathsetmacro\ymax{(\Nylines+0.4)*\d} % maximum of y = ct axis in S
\pgfmathsetmacro\xmaxp{(\Nxplines+0.4)*\D} % maximum of x' axis in S'
\pgfmathsetmacro\ymaxp{(\Nyplines+0.4)*\D} % maximum of y' = ct' axis in S'
\pgfmathsetmacro\Lz{4*\D} % proper/rest length L0 of ladder in S'
\pgfmathsetmacro\L{\Lz/cos(\ang)} % contracted length L in S
\pgfmathsetmacro\xb{4.96*\d} % x coordinate of barn in S
\pgfmathsetmacro\wb{3.08*\d} % width of barn in S
\pgfmathsetmacro\yAp{(\xb+0.04*\d)*sin(\ang)*(1-cot(\ang)^2)} % y' = ct' coordinate when ladder is fully in barn in S
\pgfmathsetmacro\yBp{\yAp+\L*sin(\ang)} % y' = ct' coordinate when ladder is fully in barn in S
\coordinate (O) at (0,0);
\coordinate (X) at (\ang:\xmax+0.05);
\coordinate (T) at (90-\ang:\ymax+0.05);
\coordinate (X') at (\xmaxp+0.15,0);
\coordinate (T') at (0,\ymaxp+0.15);
\coordinate (L) at (\ang:\L); % ladder end in S
\coordinate (L') at (\Lz,0); % ladder end in S'
\coordinate (A) at (0,\yAp); % left end of ladder when fully in barn in S
\coordinate (B) at ($(A)+(L)$); % right end of ladder when fully in barn in S
\coordinate (C) at (0,{(\xb+\wb+0.08*\d)*sin(\ang)*(1-cot(\ang)^2)}); % left end of ladder when fully passed through barn
% FILL
\fill[myfieldred]
(-\xmin,0) -| (\xmaxp,\ymaxp) -| (0,-\xmin) -| cycle;
\fill[mylightred] % ladder frame
(0,-\xmin) |- (\Lz,\ymaxp) -- ($(L)+(0,-\xmin)$) -- cycle;
\fill[mydarkblue!22] % barn frame
(\ang:\xb)++(90-\ang:-\xmin) --++ (90-\ang:\xmin+\ymax)
--++ (\ang:\wb) --++ (90-\ang:-\xmin-\ymax) -- cycle;
% HIGHLIGHT DOORS OPEN/CLOSED
\begin{scope}
\clip (0,0) --++ (90-\ang:\ymax) -- (\xmaxp+1.8*\d,\ymaxp) --++ (0,-1.1*\ymaxp) -- cycle;
\draw[myredhighlight,line width=3.1] % highlight simultaneity in S'
({\yAp*tan(\ang)-0.1},\yAp) -- (\xmaxp+1.6*\d,\yAp)
({\yBp*tan(\ang)-0.1},\yBp) -- (\xmaxp+1.8*\d,\yBp);
\draw[mypurplehighlight,line width=3.1] % highlight simultaneity in S
(A)++(\ang:-\xb-0.1) --++ (\ang:{\xb+\L+3.75*\d});
\end{scope}
% BOOSTED WORLD LINE GRID
\message{ Making world lines for boosted frame...^^J}
\foreach \i [evaluate={\x=\i*\D;}] in {1,...,\Nxplines}{
\draw[world line] (\x,0) -- (\x,\ymaxp);
}
\foreach \i [evaluate={\t=\i*\D;}] in {1,...,\Nyplines}{
\draw[world line t] (0,\t) -- (\xmaxp,\t);
}
% WORLD LINE GRID
\message{ Making world lines...^^J}
\foreach \i [evaluate={\x=\i*\d;}] in {1,...,\Nxlines}{
\draw[world line'] (\ang:\x) --++ (90-\ang:\ymax);
}
\foreach \i [evaluate={\t=\i*\d;}] in {1,...,\Nylines}{
\draw[world line'] (90-\ang:\t) --++ (\ang:\xmax);
}
% WORLD LINES BARN & ROD
\draw[->,thick,mydarkblue] % barn left door
(\ang:\xb+\wb)++(90-\ang:-\xmin) --++ (90-\ang:\xmin+\ymax+0.2);
\draw[->,thick,mydarkblue] % barn right door
(\ang:\xb)++(90-\ang:-\xmin) --++ (90-\ang:\xmin+\ymax+0.2);
\draw[->,thick,mydarkbrown] % rod right end
(L)++(0,-\xmin) -- (\Lz,\ymaxp+0.15);
% AXES
\draw[->,thick] (90-\ang:-\xmin) -- (T) node[below left=-1] {$ct$};
\draw[->,thick] (\ang:-\xmin) -- (X) node[below left=0] {$x$};
\draw[->,thick,mydarkred] (0,-\xmin) -- (T')
node[right=3,above=-1] {$ct'$};
\draw[->,thick,mydarkred] (-\xmin,0) -- (X')
node[anchor=140,inner sep=0.5] {$x'$};
% LADDER
\draw[rod] (O) -- (L)
node[pos=0.45,below=2,scale=0.8] {$L$};
\draw[rod] (O) -- (L')
node[pos=0.45,above=0.6,scale=0.8] {\contour{mylightred}{$L_0$}};
\draw[rod] (O) -- (L');
% LADDER IN BARN
\draw[rod] (A) --++ (L);
\draw[rod] (A) --++ (L');
\draw[rod] (B) --++ (-\Lz,0);
% LADDER RIGHT OF BARN
\draw[rod] (C) --++ (L');
\draw[rod] (C) --++ (L);r
% LABELS
\node[mydarkbrown,above=1,scale=0.8] at (\Lz/2,\ymaxp)
{rod};
\node[mydarkblue,below=0,scale=0.8]
at ({(\xb+\wb/2)*cos(\ang)*(1-tan(\ang)^2)+0.07},0)
{\contour{mydarkblue!22}{barn}};
%\node[mydarkblue,anchor=90-\ang,inner sep=2,scale=0.8,rotate=\ang] at (\ang:\xb+\L/2)
% {barn}; %{barn\\$L<w<L_0$};
\node[mydarkpurple,right,align=left,scale=0.65,yshift=1.6,rotate=\ang]
at ($(B)+(\ang:0.4*\d)$) {both doors closed in S};
\node[mydarkred,right,scale=0.65,yshift=1.8] at ($(A)+(\Lz+0.3*\d,0)$)
{left door closed in S$'$};
\node[mydarkred,right,scale=0.65,yshift=0.7] at ($(B)+(0.3*\d,0)$)
{right door closed in S$'$};
\end{tikzpicture}
% SPACETIME DIAGRAM of TWIN PARADOX
\begin{tikzpicture}[scale=2.0]
\message{Twin paradox^^J}
\def\xmin{0.2}
\def\xmax{2}
\def\ymax{2.3}
\def\Nlines{5} % number of world lines (at constant x/t)
\def\ang{60} % angle between ct and ct' axes
\pgfmathsetmacro\d{0.94*\xmax/\Nlines} % grid size
\pgfmathsetmacro\dt{3*\d} % time of half trip
\pgfmathsetmacro\D{\dt/tan(\ang)} % distance between observers
\pgfmathsetmacro\h{\dt-\D/tan(\ang)} % half time gap of return
\coordinate (A) at (0,0); % observer A at t=0
\coordinate (B) at (\D,0); % observer B at t=0
\coordinate (C) at (\D,\dt); % point of return
\coordinate (T1) at (0,\dt); % time of return
\coordinate (T2) at (0,2*\dt); % time of arrival
% WORLD LINES GRID
\message{ Making world lines...^^J}
\foreach \i [evaluate={\x=\i*\d;}] in {1,...,\Nlines}{
\message{ Running i/N=\i/\Nlines, x=\x...^^J}
\draw[world line] ( \x,-\xmin) -- ( \x,\ymax);
\draw[world line t] (-\xmin, \x) -- (\xmax, \x);
}
\draw[world line t] (-\xmin,{(\Nlines+1)*\d}) -- (\xmax,{(\Nlines+1)*\d});
% AXES
\draw[->,thick] (0,-\xmin) -- (0,\ymax+0.2) node[above left=-2] {$ct$};
\draw[->,thick] (-\xmin,0) -- (\xmax+0.2,0) node[below=0] {$x$};
% VECTORS
\draw[vector,myred,shorten >=1] (A) -- (T2);
\draw[vector,mygreen,shorten >=2] (A) -- (C);
\draw[vector,mygreen,shorten >=1] (C) -- (T2);
% PLANES OF SIMULTANEITY
\fill[mydarkred,opacity=0.06]
(0,\h) -- (C) -- (0,2*\dt-\h) -- cycle;
\pgfmathsetmacro\ystep{\h/3}
\foreach \i [evaluate={\dy=(\i-1)*\ystep; \ya=\i*\ystep; \yb=2*\dt-\i*\ystep;}] in {1,...,3}{
\draw[mydarkred,dashed,line width=0.6]
(0,\ya)++(90-\ang:-0.8*\xmin) --++ (90-\ang:{1.2*\xmin+\D/sin(\ang)});
\draw[mydarkblue,dashed,line width=0.6]
(0,\yb)++(\ang-90:-0.8*\xmin) --++ (\ang-90:{1.2*\xmin+\D/sin(\ang)});
\fill[mydarkred] (0,\ya) circle(0.02);
\fill[mydarkblue] (0,\yb) circle(0.02);
%\fill[mydarkblue] ({\D-\dy*cot(\ang)},\dt+\dy) circle(0.02);
%\fill[mydarkred] ({\D-\dy*cot(\ang)},\dt-\dy) circle(0.02);
\fill[mydarkblue] (C)++(-\ang:{\dy*sin(\ang)/cos(2*\ang)}) circle(0.02);
\fill[mydarkred] (C)++( \ang:{\dy*sin(\ang)/cos(2*\ang)}) circle(0.02);
}
\fill[mydarkred] (A) circle(0.04) node[below left=-1] {A}; % observer A
\fill[mydarkgreen] (C) circle(0.04)
node[right=4] {\contour{white}{B turns around}}; % observer B returns
\node[mydarkblue,above right=0,align=left] at (2*\d,1.15*\dt)
{\contour{white}{planes of}\\[-2]\contour{white}{simultaneity}};
\node[mydarkred,below right=0,align=left] at (2*\d,0.85*\dt)
{\contour{white}{planes of}\\[-2]\contour{white}{simultaneity}};
% TICKS
\node[fill=white,inner sep=1,above=1,left=3] at (T1) {$\dfrac{ct_2}{2}=ct_1$};
\node[fill=white,inner sep=1,above=2,left=3] at (T2) {$ct_2$};
\tick{T1}{0};
\tick{T2}{0};
\end{tikzpicture}
% SPACETIME DIAGRAM - INVARIANT HYPERBOLOIDS
\begin{tikzpicture}[scale=1.8]
\message{Invariant hyperboloids^^J}
% SETTINGS
\def\xmin{2.2}
\def\xmax{3.1}
\def\ymin{2.2}
\def\ymax{2.6}
\def\xmaxp{2.85} % maximum of rotated axis
\def\Nlines{4} % number of world lines (at constant x/t)
\pgfmathsetmacro\ang{atan(0.52)} % angle between x and x' axes
\pgfmathsetmacro\d{0.64*\xmax/\Nlines} % grid size
\pgfmathsetmacro\D{\d/cos(\ang)/sqrt(1-tan(\ang)^2)} % grid size, boosted
\pgfmathsetmacro\dextra{(\Nlines+1)*\d} % extra line
\pgfmathsetmacro\st{3*\d} % spacetime interval
\pgfmathsetmacro\sx{4*\d} % spacetime interval
\pgfmathsetmacro\sr{sqrt(\sx^2-\st^2)} % spacetime interval sr^2 = st^2 - sx^2 < 0
\pgfmathsetmacro\Ax{3*\D*sin(\ang)} % x coordinate of event A
\pgfmathsetmacro\Ay{3*\D*cos(\ang)} % y coordinate of event A
\pgfmathsetmacro\Bx{4*\D*cos(\ang)} % x coordinate of event B
\pgfmathsetmacro\By{4*\D*sin(\ang)} % y coordinate of event B
\pgfmathsetmacro\Cx{\Ay+\By} % x coordinate of event C' %(\Bx+tan(\ang)*\Ay)/sqrt(1-tan(\ang)^2)
\coordinate (O) at (0,0);
\coordinate (X) at (\xmax+0.2,0);
\coordinate (T) at (0,\ymax+0.2);
\coordinate (X') at (\ang:\xmaxp+0.2);
\coordinate (T') at (90-\ang:\xmaxp+0.2);
\coordinate (A) at (0,\st); % event A
\coordinate (A') at (90-\ang:3*\D); % event A', boosted A
\coordinate (B) at (\sx,0); % event A
\coordinate (B') at (\ang:4*\D); % event A', boosted A
\coordinate (C) at (4*\d,3*\d); % event C
% WORLD LINE GRID
\message{ Making world lines...^^J}
\foreach \i [evaluate={\x=\i*\d;}] in {1,...,\Nlines}{
\message{ Running i/N=\i/\Nlines, x=\x...^^J}
\draw[world line] (-\x,-\ymin) -- (-\x,\ymax);
\draw[world line] ( \x,-\ymin) -- ( \x,\ymax);
\draw[world line t] (-\xmin,-\x) -- (\xmax,-\x);
\draw[world line t] (-\xmin, \x) -- (\xmax, \x);
}
\draw[world line] (\dextra,-\ymin) -- (\dextra,\ymax);
\draw[world line] (\dextra+\d,-\ymin) -- (\dextra+\d,\ymax);
%\draw[world line'] (-\xmin,-\dextra) -- (\xmax,-\dextra);
\draw[world line'] (-\xmin,\dextra) -- (\xmax,\dextra);
% BOOSTED WORLD LINE GRID
\message{ Making world lines for boosted frame...^^J}
\fill[mydarkred,opacity=0.05]
(O) --++ (\ang:\xmaxp) --++ (90-\ang:\xmaxp) --++ (\ang:-\xmaxp) -- cycle;
\fill[mydarkred,opacity=0.05]
(O) --++ (\ang:\D-\xmaxp) --++ (90-\ang:\D-\xmaxp) --++ (\ang:\xmaxp-\D) -- cycle;
\foreach \i [evaluate={\x=\i*\D;}] in {1,...,\Nlines}{
\message{ Running i/N=\i/\Nlines, x=\x...^^J};
\ifnumcomp{\i}{<}{\Nlines}{
\draw[world line'] (\ang:-\x) --++ (90-\ang:\D-\xmaxp);
\draw[world line'] (90-\ang:-\x) --++ (\ang:\D-\xmaxp);
}{}
\draw[world line'] (\ang:\x) --++ (90-\ang:\xmaxp);
\draw[world line'] (90-\ang:\x) --++ (\ang:\xmaxp);
}
% AXES
\draw[->,thick] (0,-\ymin) -- (T) node[left=-1] {$ct$};
\draw[->,thick] (-\xmin,0) -- (X) node[below=0] {$x$};
\draw[->,thick,mydarkred] (90-\ang:\D-\xmaxp) -- (T')
node[right=2,above=-1] {$ct'$};
\draw[->,thick,mydarkred] (\ang:\D-\xmaxp) -- (X') node[below=2,right=-3] {$x'$};
% LIGHTCONE
\draw[myorange,thick]
(-1.1*\xmin,1.1*\xmin) -- (1.1*\ymin,-1.1*\ymin)
(-\xmaxp,-\xmaxp) -- (1.2*\xmaxp,1.2*\xmaxp);
% AREA HYPERBOLIC SECTORS
\fill[mygreen!90!black,opacity=0.15,thick,samples=\Nsamples,smooth,variable=\x,domain=0:\Ax]
plot(\x,{sqrt((\st)^2+(\x)^2)}) -- (O) -- (A);
\fill[mydarkblue!90!black,opacity=0.15,thick,samples=\Nsamples,smooth,variable=\y,domain=0:\By]
plot({sqrt((\sx)^2+(\y)^2)},\y) -- (O) -- (B);
\node[mydarkgreen,scale=0.92] at (89.5-\ang/2:1.97*\d)
{\contour{mygreen!90!black!15}{$\dfrac{c^2t_1^2\phi}{2}$}};
\node[mydarkblue,scale=0.92] at (\ang/2:3.1*\d)
{\contour{mydarkblue!90!black!15}{$\dfrac{x_1^2\phi}{2}$}};
% SPACELIKE HYPERBOLOIDS
\draw[mygreen,thick,samples=\Nsamples,smooth,variable=\x,domain=-\xmin:1.05*\xmax]
plot(\x,{sqrt((\st)^2+(\x)^2)});
\draw[mydarkgreen,very thick,samples=\Nsamples,variable=\x,domain=0:\Ax,
decoration={markings,mark=at position 0.58 with {\arrow{latex}}},postaction={decorate}]
plot(\x,{sqrt((\st)^2+(\x)^2)});
\node[mydarkgreen,right=1,above right=0] at (-\xmin,\ymax)
{$s^2 = c^2t^2-x^2>0$};
% TIMELIKE HYPERBOLOIDS
\draw[myred,very thick,samples=\Nsamples,variable=\y,domain=\st:\Cx,
decoration={markings,mark=at position 0.58 with {\arrow{latex}}},postaction={decorate}]
plot({sqrt(\sr^2+(\y)^2)},\y);
\draw[myblue,thick,samples=\Nsamples,smooth,variable=\y,domain=-1.05*\ymin:0.95*\ymax]
plot({sqrt(\sx^2+(\y)^2)},\y);
\draw[mydarkblue,very thick,samples=\Nsamples,variable=\y,domain=0:\By,
decoration={markings,mark=at position 0.58 with {\arrow{latex}}},postaction={decorate}]
plot({sqrt(\sx^2+(\y)^2)},\y);
\node[mydarkblue,right=0] at (0.7*\xmax,-0.25*\xmax)
{\contour{white}{$s^2 = c^2t^2-x^2<0$}};
% TICKS
\draw[mydarkgreen,dashed] ({\Ax},0) -- (A') -- (0,{\Ay});
\draw[mydarkblue,dashed] ({\Bx},0) -- (B') -- (0,{\By});
\tick{0,\st}{0} node[mydarkgreen,right=4,below left=-2.5] {$ct_1$};
\tick{\sx,0}{90} node[mydarkblue,below=1,below left=-3] {$x_1$};
\tick{0,\Ay}{0} node[mydarkgreen,above=1,left=-2]
{\contour{white}{$ct_1\cosh\phi$}};
\tick{\Ax,0}{90} node[mydarkgreen,right=4,below=-4]
{\contour{white}{$ct_1\sinh\phi$}};
\tick{\Bx,0}{90} node[mydarkblue,right=9,below=-4]
{\contour{white}{$x_1\cosh\phi$}};
\tick{0,\By}{0} node[mydarkblue,below=1,left=-2]
{\contour{white}{$x_1\sinh\phi$}};
% EVENTS
\fill[mydarkgreen] (A) circle(0.03); % event A
\fill[mydarkgreen] (A') circle(0.03); % event A'
\fill[mydarkblue] (B) circle(0.03); % event B
\fill[mydarkblue] (B') circle(0.03); % event B'
\fill[mydarkred] (C) circle(0.03); % event C
\fill[mydarkred] (\ang:4*\D)++(90-\ang:3*\D) coordinate (C') circle(0.03); % event C'
%\node[mydarkred,above=2,right=6] at (C') {$\left\{\begin{aligned}
% ct' &= ct\cosh\phi - x\sinh\phi \\
% x' &= x\cosh\phi - ct\sinh\phi
%\end{aligned}\right.$};
\end{tikzpicture}
% SPACETIME DIAGRAM - INVARIANT HYPERBOLOIDS with equations
\def\axes{ % common axes
% SETTINGS
\def\xmin{0.3}
\def\xmax{3.1}
\def\ymin{0.3}
\def\ymax{2.6}
\def\xminp{0.4} % minimum of rotated axis
\def\xmaxp{2.85} % maximum of rotated axis
\def\Nlines{4} % number of world lines (at constant x/t)
\pgfmathsetmacro\ang{atan(0.5)} % angle between x and x' axes
\pgfmathsetmacro\d{0.64*\xmax/\Nlines} % grid size
\pgfmathsetmacro\D{\d/cos(\ang)/sqrt(1-tan(\ang)^2)} % grid size, boosted
\pgfmathsetmacro\dextra{(\Nlines+1)*\d} % extra line
\pgfmathsetmacro\st{3*\d} % spacetime interval
\pgfmathsetmacro\sx{4*\d} % spacetime interval
\pgfmathsetmacro\sr{sqrt(\sx^2-\st^2)} % spacetime interval sr^2 = st^2 - sx^2 < 0
\pgfmathsetmacro\Ax{3*\D*sin(\ang)} % x coordinate of event A
\pgfmathsetmacro\Ay{3*\D*cos(\ang)} % y coordinate of event A
\pgfmathsetmacro\Bx{4*\D*cos(\ang)} % x coordinate of event B
\pgfmathsetmacro\By{4*\D*sin(\ang)} % y coordinate of event B
\pgfmathsetmacro\Cx{\Ay+\By} % x coordinate of event C' %(\Bx+tan(\ang)*\Ay)/sqrt(1-tan(\ang)^2)
\coordinate (O) at (0,0);
\coordinate (X) at (\xmax+0.2,0);
\coordinate (T) at (0,\ymax+0.2);
\coordinate (X') at (\ang:\xmaxp+0.2);
\coordinate (T') at (90-\ang:\xmaxp+0.2);
\coordinate (A) at (0,\st); % event A
\coordinate (A') at (90-\ang:3*\D); % event A', boosted A
\coordinate (B) at (\sx,0); % event A
\coordinate (B') at (\ang:4*\D); % event A', boosted A
\coordinate (C) at (4*\d,3*\d); % event C
% WORLD LINE GRID
\message{ Making world lines...^^J}
\foreach \i [evaluate={\x=\i*\d;}] in {1,...,\Nlines}{
\message{ Running i/N=\i/\Nlines, x=\x...^^J}
\draw[world line] ( \x,-\ymin) -- ( \x,\ymax);
\draw[world line t] (-\xmin, \x) -- (\xmax, \x);
}
\draw[world line] (\dextra,-\ymin) -- (\dextra,\ymax);
\draw[world line] (\dextra+\d,-\ymin) -- (\dextra+\d,\ymax);
\draw[world line'] (-\xmin,\dextra) -- (\xmax,\dextra);
% BOOSTED WORLD LINE GRID
\message{ Making world lines for boosted frame...^^J}
\fill[mydarkred,opacity=0.05]
(O) --++ (\ang:\xmaxp) --++ (90-\ang:\xmaxp) --++ (\ang:-\xmaxp) -- cycle;
\fill[mydarkred,opacity=0.05]
(O) --++ (\ang-180:\xminp) --++ (-90-\ang:\xminp) --++ (\ang:\xminp) -- cycle;
\foreach \i [evaluate={\x=\i*\D;}] in {1,...,\Nlines}{
\message{ Running i/N=\i/\Nlines, x=\x...^^J};
\draw[world line'] (\ang:\x) --++ (90-\ang:\xmaxp);
\draw[world line'] (90-\ang:\x) --++ (\ang:\xmaxp);
}
% AXES
\draw[->,thick] (0,-\ymin) -- (T) node[left=-1] {$ct$};
\draw[->,thick] (-\xmin,0) -- (X) node[below=0] {$x$};
\draw[->,thick,mydarkred] (-90-\ang:\xminp) -- (T')
node[right=2,above=-1] {$ct'$};
\draw[->,thick,mydarkred] (\ang-180:\xminp) -- (X') node[below=2,right=-3] {$x'$};
% LIGHTCONE
\draw[myorange,thick]
(-1.1*\xminp,1.1*\xminp) -- (1.1*\xminp,-1.1*\xminp)
(-1.3*\xminp,-1.3*\xminp) -- (1.2*\xmaxp,1.2*\xmaxp);
% SPACELIKE HYPERBOLOIDS
\draw[mygreen,thick,samples=\Nsamples,smooth,variable=\x,domain=-1.6*\xmin:1.05*\xmax]
plot(\x,{sqrt((\st)^2+(\x)^2)});
\draw[mydarkgreen,very thick,samples=\Nsamples,variable=\x,domain=0:\Ax,
decoration={markings,mark=at position 0.58 with {\arrow{latex}}},postaction={decorate}]
plot(\x,{sqrt((\st)^2+(\x)^2)});
\node[mydarkgreen,above left=-2] at (\xmax,{sqrt((\st)^2+(\xmax)^2)})
{$s^2 = c^2t^2-x^2>0$};
% TIMELIKE HYPERBOLOIDS
\draw[myred,very thick,samples=\Nsamples,variable=\y,domain=\st:\Cx,
decoration={markings,mark=at position 0.58 with {\arrow{latex}}},postaction={decorate}]
plot({sqrt(\sr^2+(\y)^2)},\y);
\draw[myblue,thick,samples=\Nsamples,smooth,variable=\y,domain=-1.6*\ymin:0.95*\ymax]
plot({sqrt(\sx^2+(\y)^2)},\y);
\draw[mydarkblue,very thick,samples=\Nsamples,variable=\y,domain=0:\By,
decoration={markings,mark=at position 0.58 with {\arrow{latex}}},postaction={decorate}]
plot({sqrt(\sx^2+(\y)^2)},\y);
\node[mydarkblue,below=0] at (0.7*\xmax,-1.6*\xmin)
{$s^2 = c^2t^2-x^2<0$};
% TICKS
\draw[mydarkgreen,dashed] ({\Ax},0) -- (A') -- (0,{\Ay});
\draw[mydarkblue,dashed] ({\Bx},0) -- (B') -- (0,{\By});
\tick{0,\st}{0} node[mydarkgreen,right=4,below left=-2] {$ct_1$};
\tick{\sx,0}{90} node[mydarkblue,below=1,below left=-3] {$x_1$};
% EVENTS
\fill[mydarkgreen] (A) circle(0.03); % event A
\fill[mydarkgreen] (A') circle(0.03); % event A'
\fill[mydarkblue] (B) circle(0.03); % event B
\fill[mydarkblue] (B') circle(0.03); % event B'
\fill[mydarkred] (C) circle(0.03); % event C
\fill[mydarkred] (\ang:4*\D)++(90-\ang:3*\D) coordinate (C') circle(0.03); % event C'
}
\begin{tikzpicture}[scale=2]
\message{Invariant hyperboloids with equations^^J}
% AXES
\axes
\node[mydarkgreen,below=1] at (\Ax/2,{sqrt((\st)^2+(\Ax/2)^2)}) {$\phi$};
\node[mydarkblue,left=1.5] at ({sqrt(\sx^2+(0.54*\By)^2)},0.54*\By) {\contour{white}{$\phi$}};
% TICKS
\tick{0,\Ay}{0} node[mydarkgreen,above=0,left=-2]
{$ct_1\cosh\phi$};
\tick{\Ax,0}{90} node[mydarkgreen,right=4,below=-4]
{\contour{white}{$ct_1\sinh\phi$}};
\tick{\Bx,0}{90} node[mydarkblue,right=8,below=-4]
{\contour{white}{$x_1\cosh\phi$}};
\tick{0,\By}{0} node[mydarkblue,below=0,left=-2]
{$x_1\sinh\phi$};
% EVENT LABELS
\node[mydarkred,anchor=0,inner sep=3] at (C) {\contour{myfieldred}{R}};
\node[mydarkred,below right] at (1.0*\xmax,3.57*\d) {$
\begin{aligned}
%\mathrm{R} &= (x_1,ct_1) \\
% &= (x_1\cosh\phi-ct_1\sinh\phi,\\[-0.3em]
% &\hspace{1.7em} ct_1\cosh\phi-x_1\sinh\phi)\\
\mathrm{R}
&=
\left\{\begin{aligned}
ct &= ct_1 \\
x &= x_1
\end{aligned}\right.\\
&=
\left\{\begin{aligned}
ct' &= ct_1\cosh\phi - x_1\sinh\phi \\
x' &= x_1\cosh\phi - ct_1\sinh\phi
\end{aligned}\right.
\end{aligned}
$};
%\node[mydarkred,anchor=-173,inner sep=3] at (C') {\contour{myfieldred}{R$'$}};
\node[mydarkred,anchor=167,inner sep=3] at (C') {$
\begin{aligned}
\mathrm{\contour{myfieldred}{R$'$}}
&=
\left\{\begin{aligned}
ct &= ct_1\cosh\phi + x_1\sinh\phi \\
x &= x_1\cosh\phi + ct_1\sinh\phi
\end{aligned}\right.\\
&=
\left\{\begin{aligned}
ct' &= ct_1 \\
x' &= x_1
\end{aligned}\right.
\end{aligned}
$};
\end{tikzpicture}
% SPACETIME DIAGRAM - INVARIANT HYPERBOLOIDS with equations 2
\begin{tikzpicture}[scale=2]
\message{Invariant hyperboloids with equations 2^^J}
% AXES
\axes
% TICKS
\tick{0,\Ay}{0} node[mydarkgreen,above=0,left=-2]
{$\gamma ct_1$};
\tick{\Ax,0}{90} node[mydarkgreen,right=1,below=-1]
{\contour{white}{$\gamma\beta ct_1$}};
\tick{\Bx,0}{90} node[mydarkblue,right=0,below=-1]
{\contour{white}{$\gamma x_1$}};
\tick{0,\By}{0} node[mydarkblue,below=0,left=-2]
{$\gamma\beta x_1$};
% EVENT LABELS
\node[mydarkred,anchor=0,inner sep=3] at (C) {\contour{myfieldred}{R}};
\node[mydarkred,below right] at (1.0*\xmax,3.57*\d) {$
\begin{aligned}
\mathrm{R}
&=
\left\{\begin{aligned}
ct &= ct_1 \\
x &= x_1
\end{aligned}\right.\\
&=
\left\{\begin{aligned}
ct' &= \gamma(ct_1 - \beta x_1) \\
x' &= \gamma( x_1 - \beta ct_1)
\end{aligned}\right.
\end{aligned}
$};
%\node[mydarkred,anchor=-173,inner sep=3] at (C') {\contour{myfieldred}{R$'$}};
\node[mydarkred,anchor=167,inner sep=3] at (C') {$
\begin{aligned}
\mathrm{\contour{myfieldred}{R$'$}}
&=
\left\{\begin{aligned}
ct &= \gamma(ct_1 + \beta x_1) \\
x &= \gamma( x_1 + \beta ct_1)
\end{aligned}\right.\\
&=
\left\{\begin{aligned}
ct' &= ct_1 \\
x' &= x_1
\end{aligned}\right.
\end{aligned}
$};
\end{tikzpicture}
% LORENTZ TRANSFORMATION MATRIX
\begin{tikzpicture}[scale=1]
\node[align=left] at (0,0) {
\begin{minipage}{7.5cm}
Lorentz transformation in the $x$ direction
\begin{align*}
\begin{pmatrix}
ct' \\
x' \\
y' \\
z'
\end{pmatrix}
&=
\begin{pmatrix}
\gamma & -\beta\gamma & 0 & 0 \\
-\beta\gamma & \gamma & 0 & 0 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0
\end{pmatrix}
\begin{pmatrix}
ct \\
x \\
y \\
zw
\end{pmatrix}\\
&=
\begin{pmatrix}
\cosh\phi & -\sinh\phi & 0 & 0 \\
-\sinh\phi & \cosh\phi & 0 & 0 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0
\end{pmatrix}
\begin{pmatrix}
ct \\
x \\
y \\
z
\end{pmatrix}
\end{align*}
\end{minipage}
};
\end{tikzpicture}
% SPACETIME DIAGRAM - MULTIPLE INVARIANT HYPERBOLOIDS
% Inspiration: https://commons.wikimedia.org/wiki/File:Spacelike_and_Timelike_Invariant_Hyperbolas.png
\begin{tikzpicture}[scale=1.8]
\message{Multiple invariant hyperboloids^^J}
\def\xmax{2}
\def\Nlines{4} % number of world lines (at constant x/t)
\pgfmathsetmacro\w{\xmax/(\Nlines+1)}
% AXES
\draw[->,thick] (0,-\xmax) -- (0,\xmax+0.2) node[left=-1] {$ct$};
\draw[->,thick] (-\xmax,0) -- (\xmax+0.2,0) node[right=-1] {$x$};
% LIGHTCONE
\draw[myorange,thick] (-\xmax,-\xmax) -- (\xmax, \xmax);
\draw[myorange,thick] (-\xmax, \xmax) -- (\xmax,-\xmax);
\foreach \i [evaluate={\s=\xmax*\i/(\Nlines+1); \xm=sqrt(\xmax^2-\s^2);}] in {1,...,\Nlines}{
% SPACELIKE HYPERBOLOIDS
\draw[mygreen,thick,samples=\Nsamples,smooth,variable=\x,domain=-\xm:\xm]
plot(\x,-{sqrt(\s^2+(\x)^2)})
plot(\x,{sqrt(\s^2+(\x)^2)});
% TIMELIKE HYPERBOLOIDS
\draw[myblue,thick,samples=\Nsamples,smooth,variable=\y,domain=-\xm:\xm]
plot(-{sqrt(\s^2+(\y)^2)},\y)
plot({sqrt(\s^2+(\y)^2)},\y);
}
% LABELS
\node[mydarkgreen,above left=2,align=center] at (-0.2*\xmax,\xmax)
{timelike separation\\[-1]$s^2 = c^2t^2 - x^2 > 0$};
\node[mydarkorange,left=2,above right=-2,align=center] at (\xmax,\xmax)
{lightlike separation\\[-1]$s^2 = c^2t^2 - x^2 = 0$};
\node[mydarkblue,right=0,align=center] at (0.88*\xmax,-0.24*\xmax)
{spacelike separation\\[-1]$s^2 = c^2t^2 - x^2 < 0$};
% VECTORS
\def\xa{0.5}
\def\xb{2.7}
\def\ta{-0.7}
\def\tb{1.7}
\draw[mydarkgreen,very thick,decoration={markings,mark=at position 0.55 with {\arrow{latex}}},
postaction={decorate},samples=20,variable=\x,domain=\xa:\xb]
plot({\w*\x},{\w*sqrt((\x)^2+3^2)});
\draw[mydarkblue,very thick,decoration={markings,mark=at position 0.6 with {\arrow{latex}}},
postaction={decorate},samples=20,variable=\x,domain=\ta:\tb]
plot({\w*sqrt((\x)^2+3^2)},{\w*\x});
\fill[mydarkgreen] ({\w*\xa},{\w*sqrt(\xa^2+3^2)}) coordinate (A) circle(0.03);
\fill[mydarkgreen] ({\w*\xb},{\w*sqrt(\xb^2+3^2)}) coordinate (A') circle(0.03);
\fill[mydarkblue] ({(\w*sqrt((\ta)^2+3^2)},{\w*\ta}) coordinate (B) circle(0.03);
\fill[mydarkblue] ({(\w*sqrt((\tb)^2+3^2)},{\w*\tb}) coordinate (B') circle(0.03);
\draw[vector',mydarkgreen] (0,0) -- (A)
node[pos=0.53,right=-2] {$s$};
\draw[vector',mydarkgreen] (0,0) -- (A')
node[pos=0.57,right=-2] {$s$};
\draw[vector',mydarkblue] (0,0) -- (B)
node[pos=0.53,below=-1] {$s$};
\draw[vector',mydarkblue] (0,0) -- (B')
node[pos=0.53,above=-1] {$s$};
\end{tikzpicture}
% ROTATION MATRIX
\begin{tikzpicture}[scale=1]
\node[align=left] at (0,0) {
\begin{minipage}{7.5cm}
Counterclockwise rotation in the $xy$ plane
\begin{align*}
\begin{pmatrix}
ct' \\
x' \\
y' \\
z'
\end{pmatrix}
&=
\begin{pmatrix}
0 & 0 & 0 & 0 \\
0 & \cos\theta & -\sin\theta & 0 \\
0 & \sin\theta & \cos\theta & 0 \\
0 & 0 & 0 & 0
\end{pmatrix}
\begin{pmatrix}
ct \\
x \\
y \\
z
\end{pmatrix}
\end{align*}
\end{minipage}
};
\end{tikzpicture}
% SPACE DIAGRAM - MULTIPLE INVARIANT SPHERES (SPACETIME SLICES)
\begin{tikzpicture}[scale=1.8]
\message{Multiple invariant spheres^^J}
\def\xmax{2}
\def\Rmax{0.95*\xmax} % outermost radius
\def\R{\Rmax*4/\Nlines} % radius
\def\anga{25} % start angle
\def\angb{65} % end angle
\def\Nlines{6} % number of world lines (at constant x/t)
\coordinate (O) at (0,0);
\coordinate (A) at (\anga:\R);
\coordinate (B) at (\angb:\R);
% AXES
\draw[->,thick] (0,-\xmax) -- (0,\xmax+0.2) node[left=-1] {$y$};
\draw[->,thick] (-\xmax,0) -- (\xmax+0.2,0) node[below=0] {$x$};
% SPACELIKE SPHERES
\foreach \i [evaluate={\r=\Rmax*\i/\Nlines;}] in {1,...,\Nlines}{
\draw[myblue,thick] (0,0) circle(\r);
}
% LABELS
\fill[mydarkblue] (A) circle(0.03);
\fill[mydarkblue] (B) circle(0.03);
\node[mydarkblue,left=0] at (100:\xmax) {$r^2 = x^2 + y^2 > 0$};
\node[mydarkblue,right=2,align=center] at (70:\xmax)
{spacelike separation\\[-1]$s^2 = - x^2 - y^2 < 0$\\[-1]for $t=0$};
\draw[vector',mydarkblue] (0,0) -- (A) node[pos=0.59,below right=-2] {$r$};
\draw[vector',mydarkblue] (0,0) -- (B) node[pos=0.57,above left=-3] {$r$};
\draw pic[->,"$\theta$",draw=black,angle radius=20,angle eccentricity=1.3] {angle = A--O--B};
\draw[mydarkblue,very thick,decoration={markings,mark=at position 0.55 with {\arrow{latex}}},
postaction={decorate}]
(A) arc(\anga:\angb:\R);
\end{tikzpicture}
% SPACE DIAGRAM - MULTIPLE INVARIANT SPHERES (SPACETIME SLICES)
\begin{tikzpicture}[scale=1.8]
\message{Multiple invariant spheres^^J}
\def\xmax{2}
\def\Rmax{0.95*\xmax}
\def\Nlines{8} % number of world lines (at constant x/t)
% AXES
\draw[->,thick] (0,-\xmax) -- (0,\xmax+0.2) node[left=-1] {$y$};
\draw[->,thick] (-\xmax,0) -- (\xmax+0.2,0) node[below=0] {$x$};
% SPHERES
\foreach \i [evaluate={\R=\Rmax*\i/\Nlines;}] in {1,...,3}{
\draw[mygreen,thick] (0,0) circle(\R); % timelike separation
}
\draw[myorange,thick] (0,0) circle(\Rmax*4/\Nlines); % light cone
\foreach \i [evaluate={\R=\Rmax*\i/\Nlines;}] in {5,...,\Nlines}{
\draw[myblue,thick] (0,0) circle(\R); % spacelike separation
}
% LABELS
\node[mydarkgreen,scale=0.9] at (50:\Rmax*2/\Nlines) {\contour{white}{$s^2>0$}};
\node[mydarkorange,scale=0.9] at (50:\Rmax*4/\Nlines) {\contour{white}{$s^2=0$}};
\node[mydarkblue,scale=0.9] at (50:\Rmax*7/\Nlines) {\contour{white}{$s^2<0$}};
\node[mydarkblue,left=0] at (100:\xmax) {$r^2 = x^2 + y^2 > 0$};
\node[mydarkblue,right=2,align=right] at (62:1.03*\xmax)
{spacetime separation\\[-1]$s^2 = c^2t^2 - x^2 - y^2$\\[-1]from $(t,r)=(0,0)$};
\end{tikzpicture}
% LORENTZ FACTOR
\begin{tikzpicture}[scale=1.8]
\message{Lorentz factor^^J}
\def\xmax{2.9}
\def\ymax{2.1}
\def\A{0.2} % amplitude / y scale
\pgfmathsetmacro\c{0.94*\xmax} % speed of light
\coordinate (O) at (0,0);
% AXES
\draw[->,thick] (-0.2,0) -- (\xmax+0.2,0) node[below=1] {$v$};
\draw[->,thick] (0,-0.2) -- (0,\ymax+0.2) node[below=3,left=0] {$\gamma$};
% GRID
\foreach \i in {1,...,10}{
\draw[black!20,very thin] (0,\i*\A) --++ (\c,0);
\draw[black!20,very thin] (\i*\c/10,0) --++ (0,10*\A);
}
% PLOT
\draw[dashed] (0,\A) --++ (\xmax,0);
\draw[dashed] (\c,0) --++ (0,\ymax);
\draw[dashed] (0.9*\c,0) |- (0,{\A/sqrt(1-0.9^2)});
\draw[myblue,thick,samples=2*\Nsamples,smooth,variable=\v,domain=0:{\c*sqrt(1-(\A/\ymax)^2)}]
plot(\v,\fpeval{\A/sqrt(1-(\v/\c)^2)});
\node[myblue,below=1] at (0.6*\xmax,10*\A)
{\contour{white}{$\gamma=\dfrac{1}{\sqrt{1-\frac{v^2}{c^2}}}$}};
% TICKS
\tick{\c/2,0}{90} node[right=1,below=-3] {$c/2$};
\tick{0.9*\c,0}{90} node[left=3,below=-2] {$0.9c$};
\tick{\c,0}{90} node[below=0] {$c$};
\foreach \i in {1,...,10}{
\tick{0,\i*\A}{0} node[left,scale=0.9] {$\i$};
}
\end{tikzpicture}
% LORENTZ FACTOR
\begin{tikzpicture}[scale=1.8]
\message{Lorentz factor^^J}
\def\xmax{2.9}
\def\ymax{2.1}
\def\A{0.2} % amplitude / y scale
\pgfmathsetmacro\c{0.94*\xmax} % speed of light
\coordinate (O) at (0,0);
% AXES
\draw[->,thick] (-0.2,0) -- (\xmax+0.2,0) node[left=4,below right=-3] {$\beta=\dfrac{v}{c}$};
\draw[->,thick] (0,-0.2) -- (0,\ymax+0.2) node[below=3,left=0] {$\gamma$};
% GRID
\foreach \i in {1,...,10}{
\draw[black!20,very thin] (0,\i*\A) --++ (\c,0);
\draw[black!20,very thin] (\i*\c/10,0) --++ (0,10*\A);
}
% PLOT
\draw[dashed] (0,\A) --++ (\xmax,0);
\draw[dashed] (\c,0) --++ (0,\ymax);
\draw[dashed] (0.9*\c,0) |- (0,{\A/sqrt(1-0.9^2)});
\draw[myblue,thick,samples=2*\Nsamples,smooth,variable=\v,domain=0:{\c*sqrt(1-(\A/\ymax)^2)}]
plot(\v,\fpeval{\A/sqrt(1-(\v/\c)^2)});
\node[myblue,below=1] at (0.6*\xmax,10*\A)
{\contour{white}{$\gamma=\dfrac{1}{\sqrt{1-\beta^2}}$}};
% TICKS
\tick{\c/2,0}{90} node[right=1,below=-1] {$0.5$};
\tick{0.9*\c,0}{90} node[left=3,below=-1] {$0.9$};
\tick{\c,0}{90} node[below=-1] {$1$};
\foreach \i in {1,...,10}{
\tick{0,\i*\A}{0} node[left,scale=0.9] {$\i$};
}
\end{tikzpicture}
\end{document}Click to download: relativity_minkowski_diagram.tex • relativity_minkowski_diagram.pdf
Open in Overleaf: relativity_minkowski_diagram.tex
Very helpful figures! Thank you!! Found one typo: In Fig. 6, one of the orange arrows is lablelled timelike but it should be lightlike.
Hi Cyrus,
Thank you so much for pointing that out, I really appreciate that! I was probably copy-pasting without carefully reviewing the output. It is now corrected.
Hope it did not confuse anyone, because this post has been out for a while… 😅
Please let me know if you find any other issues.
Cheers,
Izaak
These diagrams are perfect and thank you very very much! I am teaching this to a Romanian Year 12 at the moment and was looking for good diagrams. You have put a lot into his and I am extremely grateful.
Thank you very much for your message, and good luck!
Hello! Firstly, I would like to congratulate you on your excellent work, which will be very useful in my classes. Secondly, I have a question: in line 1004 of the LaTeX code, shouldn’t it be $\Delta x$ instead of $\Delta x’$?
Hi Herbert! Thank you kindly for your correction! I think you are right, it should be without a prime in that line. It is now corrected in this post. Good luck with teaching! Izaak
There is a type of Space-Time diagram in which the scale for both systems is the same. They are called “Loedel Palumbo Diagrams” and with them any analysis of special relativity is significantly simpler. They were developed in the mid-20th century by the Uruguayan physicist Enrique Loedel Palumbo from the simple, but brilliant idea, of considering in a diagram of Minkowski not one, but two “mobile” systems with the same speed, but in opposite directions and then remove the “fixed” system from the middle and… voila! you have two systems with the same scale! .The relative speed between these two systems is now given by the sine of the angle between the axes, not by the tangetic and trigonometry is that of all life. It is a shame that they are not very widespread.
This is a link to the demo
https://www.youtube.com/watch?v=o4kKeG8PyyM