Cylinder Paraboloid

Edit and compile if you like:

\documentclass{article}
%
% File name: cylinder-paraboloid.tex
% Description:
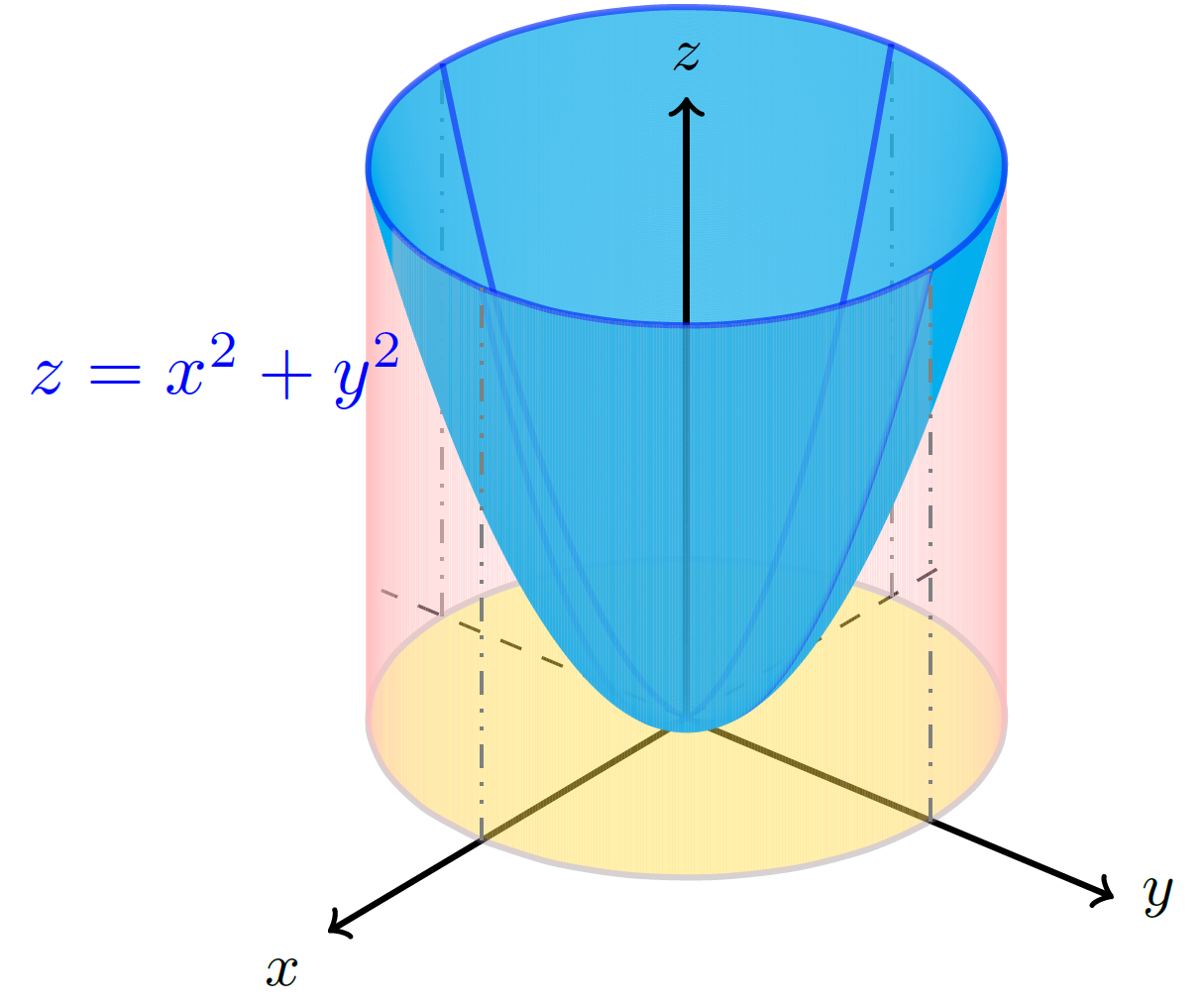
% A solid bounded by the following surfaces
% z = 0
% z = x^{2} + y^{2}
% x^{2} + y^{2} = 1
% is generated. I.e., a paraboloid and a cylinder for x^2 + y^2 \leq 1, and z \geq 0.
% 
% Date of creation: April, 23rd, 2022.
% Date of last modification: April, 23rd, 2022.
% Author: Efraín Soto Apolinar.
% https://www.aprendematematicas.org.mx/author/efrain-soto-apolinar/instructing-courses/
% Terms of use:
% According to TikZ.net
% https://creativecommons.org/licenses/by-nc-sa/4.0/
% 
\usepackage{tikz}
\usetikzlibrary{patterns}
\usepackage{tikz-3dplot}
\usetikzlibrary{math}
\usepackage[active,tightpage]{preview}
\PreviewEnvironment{tikzpicture}
\setlength\PreviewBorder{1pt}
%
\begin{document}
	%
	\tdplotsetmaincoords{60}{130}
	\begin{tikzpicture}[tdplot_main_coords,scale=0.75]
		\tikzmath{function f(\x) {return \x;};}
		\pgfmathsetmacro{\zini}{0.5*sqrt(2.0)}
		\pgfmathsetmacro{\step}{0.01}
		\pgfmathsetmacro{\zsig}{\zini+\step}
		\pgfmathsetmacro{\nextz}{\zini+0.5*\step}
		\pgfmathsetmacro{\sig}{2.0*\step}
		\pgfmathsetmacro{\tini}{0.5*pi}
		\pgfmathsetmacro{\tnext}{\tini+\step}
		\pgfmathsetmacro{\tfin}{1.85*pi}
		\pgfmathsetmacro{\tend}{2.5*pi}
		\pgfmathsetmacro{\tNext}{\tfin+\step}
		\pgfmathsetmacro{\final}{2.0*pi}
		%%% Coordinate axis
		\draw[thick,->] (0,0,0) -- (3.5,0,0) node [below left] {\footnotesize$x$};
		\draw[dashed] (0,0,0) -- (-2.5,0,0);
		\draw[thick,->] (0,0,0) -- (0,3.5,0) node [right] {\footnotesize$y$};
		\draw[dashed] (0,0,0) -- (0,-2.5,0);
		% The region of integration
		\draw[gray,thick,fill=yellow,opacity=0.35] plot[domain=0:6.2832,smooth,variable=\t] ({2.0*cos(\t r)},{2.0*sin(\t r)},{0.0}); 
		%	
		\draw[gray,dash dot dot] (-2,0,0) -- (-2,0,4);
		\draw[gray,dash dot dot] (0,-2,0) -- (0,-2,4);
		% The cylinder around the paraboloid (back)
		\foreach \angulo in {\tini,\tnext,...,\tfin}{
			\pgfmathparse{2.0*cos(\angulo r)}
			\pgfmathsetmacro{\px}{\pgfmathresult}
			\pgfmathparse{2.0*sin(\angulo r)}
			\pgfmathsetmacro{\py}{\pgfmathresult}
			\draw[pink,opacity=0.15] (\px,\py,0) -- (\px,\py,4.0);
		}		
		% The paraboloid (for z = constant)
		\foreach \altura in {\step,\sig,...,4.0}{
			\pgfmathparse{sqrt(\altura)}
			\pgfmathsetmacro{\radio}{\pgfmathresult}
			\draw[cyan,thick,opacity=0.25] plot[domain=\tini:\tfin,smooth,variable=\t] ({\radio*cos(\t r)},{\radio*sin(\t r)},{\altura}); 
		}
		\draw[thick] (0,0,0) -- (0,0,4.0); % Parte inferior al plano z = 4 (eje z)
		% LThe curves bounding the solid.
		\draw[blue,thick,opacity=0.5] plot[domain=-2:2,smooth,variable=\t] ({\t},0,{\t*\t}); 
		\draw[blue,thick,opacity=0.5] plot[domain=-2:2,smooth,variable=\t] (0,{\t},{\t*\t}); 
		% The paraboloid (for z = constant)
		\foreach \altura in {\step,\sig,...,4.0}{
			\pgfmathparse{sqrt(\altura)}
			\pgfmathsetmacro{\radio}{\pgfmathresult}
			\draw[cyan,thick,opacity=0.25] plot[domain=\tfin:\tend,smooth,variable=\t] ({\radio*cos(\t r)},{\radio*sin(\t r)},{\altura}); 
		}
		%
		\draw[blue,thick,opacity=0.5] plot[domain=0:6.2832,smooth,variable=\t] ({2.0*cos(\t r)},{2.0*sin(\t r)},{4.0});
		% The cylinder out of the paraboloid (front)
		\foreach \angulo in {\tfin,\tNext,...,\tend}{
			\pgfmathparse{2.0*cos(\angulo r)}
			\pgfmathsetmacro{\px}{\pgfmathresult}
			\pgfmathparse{2.0*sin(\angulo r)}
			\pgfmathsetmacro{\py}{\pgfmathresult}
			\draw[pink,opacity=0.15] (\px,\py,0) -- (\px,\py,4.0);
		}
		%
		\draw[gray,dash dot dot] (2,0,0) -- (2,0,4);
		\draw[gray,dash dot dot] (0,2,0) -- (0,2,4);
		%
		\node[blue,left] at (1,-1.25,2.5) {$z = x^2 + y^2$};
		\draw[thick,->] (0,0,4.0) -- (0,0,4.5) node [above] {\footnotesize$z$};	
	\end{tikzpicture}
\end{document}