Cylinder to Plane

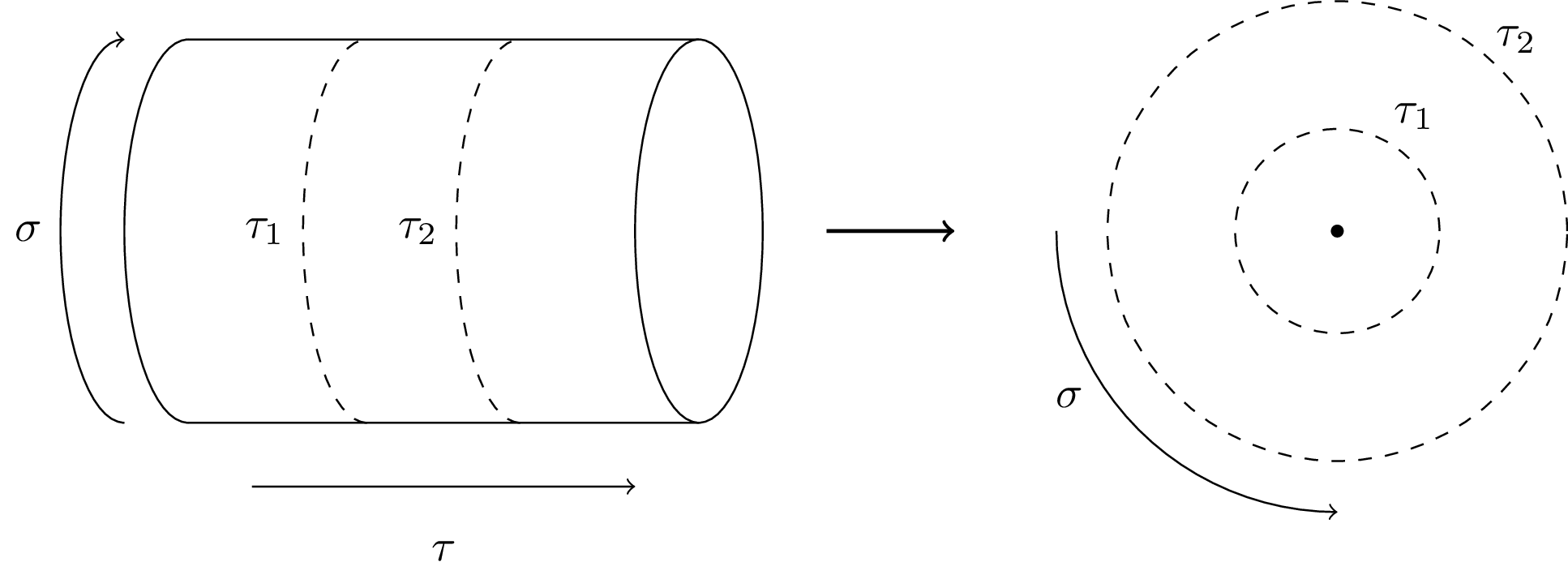
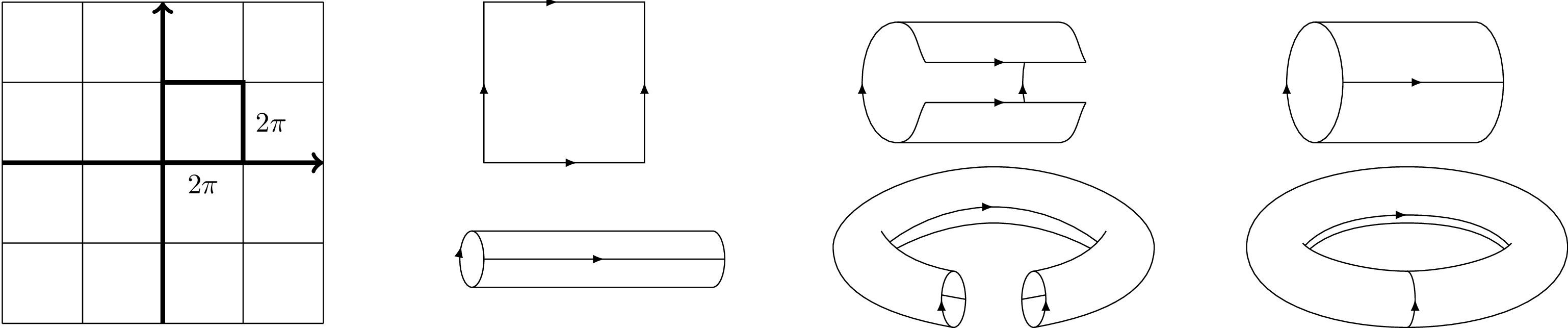
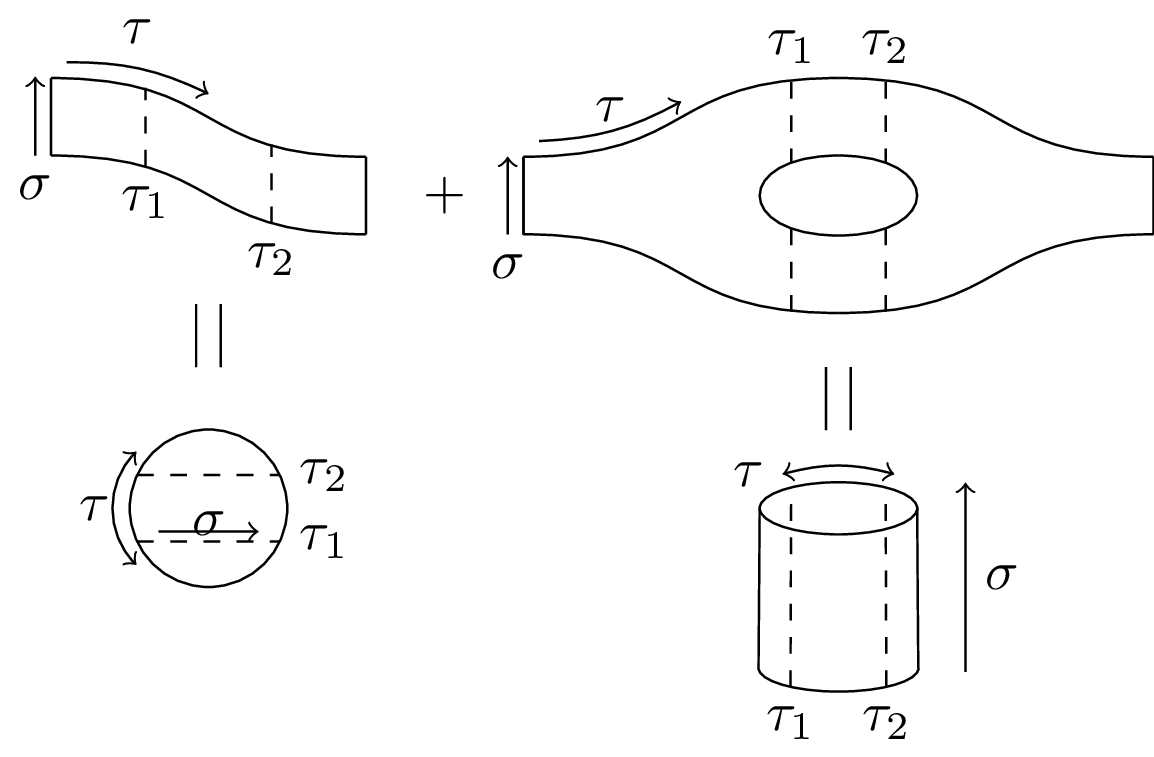
String theory: Primary fields and radial quantization A time-ordered product of fields on the cylinder maps to a radially ordered product in the complex plane. This graphic visualizes how different times on the cylinder correspond to different times on the plane.

Edit and compile if you like:

% String theory: Primary fields and radial quantization
% A time-ordered product of fields on the cylinder maps to a radially ordered product in the complex plane.
% This graphic visualizes how different times on the cylinder correspond to different times on the plane.

\documentclass[tikz]{standalone}

\begin{document}
\begin{tikzpicture}

  \draw[dashed] (2.6,0) arc (-90:90:-0.5 and 1.5);% line 1
  \draw[dashed] (1.4,0) arc (-90:90:-0.5 and 1.5);% line 2
  \draw[->] (-0.5,0) arc (-90:90:-0.5 and 1.5);
  \draw (0,0) -- (4,0);% bottom line
  \draw (0,3) -- (4,3);% top line
  \draw (0,0) arc (270:90:0.5 and 1.5);% left half of the left ellipse
  \draw (4,1.5) ellipse (0.5 and 1.5);% right ellipse
  \draw (0.6,1.5) node {$\tau_1$};
  \draw (1.8,1.5) node {$\tau_2$};
  \draw (-1.25,1.5) node {$\sigma$};
  \draw[->] (0.5,-0.5) -- (3.5,-0.5);
  \draw (2,-1) node {$\tau$};

  \draw[->,thick] (5.0,1.5) -- (6,1.5);

  \draw[dashed] (9,1.5) circle (0.8);
  \draw[dashed] (9,1.5) circle (1.8);
  \draw [->,domain=0:90] plot ({9 - 2.2*cos(\x)},{1.5-2.2*sin(\x)});
  \draw (6.9,0.2) node {$\sigma$};
  \draw (9.6,2.4) node {$\tau_1$};
  \draw (10.4,3) node {$\tau_2$};
  \node at (9,1.5) [circle,inner sep=1pt,fill=black] {};

\end{tikzpicture}
\end{document}