Cylinder Truncated by Plane

Edit and compile if you like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
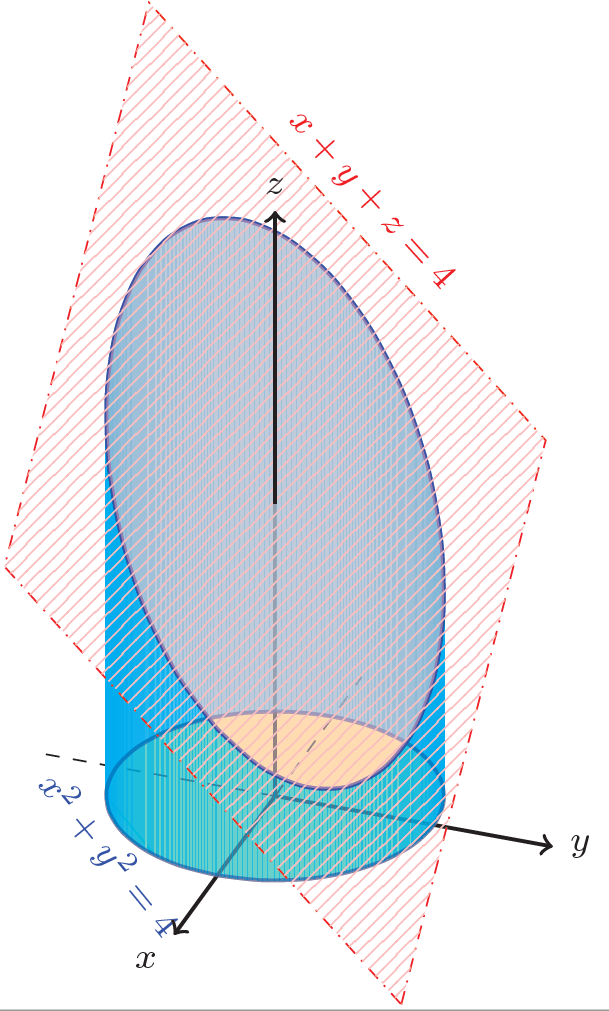
\documentclass{article}
%
% File name: cylinder-truncated-by-plane.tex
% Description: 
% A solid bounded by the following surfaces
% z = 0
% x^{2} + y^{2} = 4
% x + y + z = 4
% is generated. I.e., the intersection of a cylinder with a plane 
% for z >= 0.
% 
% Date of creation: April, 23rd, 2022.
% Date of last modification: April, 23rd, 2022.
% Author: Efraín Soto Apolinar.
% https://www.aprendematematicas.org.mx/author/efrain-soto-apolinar/instructing-courses/
% Terms of use:
% According to TikZ.net
% https://creativecommons.org/licenses/by-nc-sa/4.0/
% 
\usepackage{tikz}
\usetikzlibrary{patterns}
\usepackage{tikz-3dplot}
\usetikzlibrary{math}
\usepackage[active,tightpage]{preview}
\PreviewEnvironment{tikzpicture}
\setlength\PreviewBorder{1pt}
%
\begin{document}
    %
    \tdplotsetmaincoords{60}{110}
    \begin{tikzpicture}[tdplot_main_coords,scale=0.65]
        \tikzmath{function a(\x,\y) {return (4.0-\x-\y);};}
        \pgfmathsetmacro{\final}{2.0*pi}
        \pgfmathsetmacro{\ejez}{a(0,0)}
        % The equation of the cyrcumference
        \draw[white] (0,-2.5,0) -- (2.75,0,0) node[blue,midway,below,sloped] {\footnotesize$x^2 + y^2 = 4$};
        % The region of integration: the circle of radius 2
        \draw[thick,fill=yellow,opacity=0.5] plot[domain=0:6.2832,smooth,variable=\t] ({2.0*cos(\t r)},{2.0*sin(\t r)},{0.0});
        %%% Coordinate axis
        \draw[thick,->] (0,0,0) -- (3.5,0,0) node [below left] {\footnotesize$x$};
        \draw[dashed] (0,0,0) -- (-3,0,0);
 
 
הההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההה
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX