Parametric Sphere

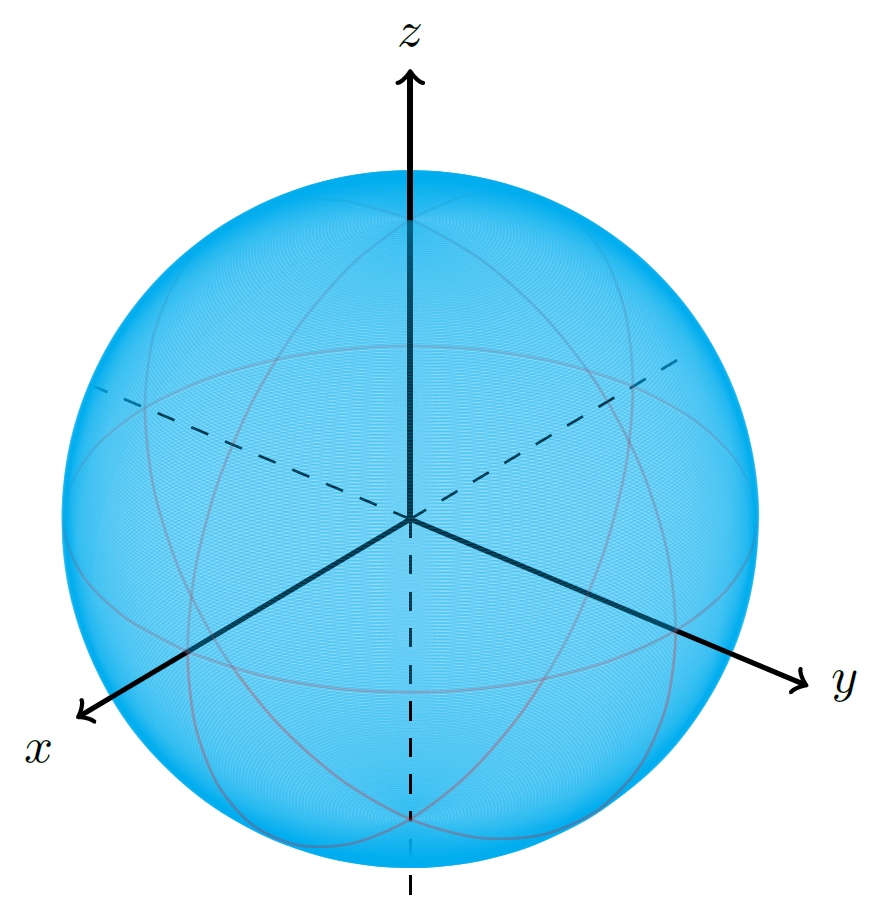
Edit and compile if you like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
\documentclass{article}
%
% File name: sphere.tex
% Description: 
% A sphere of radius a is drawn 
% by means of its parametric equations 
% (in spherical coordinates.)
% 
% Date of creation: April, 23rd, 2022.
% Date of last modification: April, 23rd, 2022.
% Author: Efraín Soto Apolinar.
% https://www.aprendematematicas.org.mx/author/efrain-soto-apolinar/instructing-courses/
% Terms of use:
% According to TikZ.net
% https://creativecommons.org/licenses/by-nc-sa/4.0/
% 
\usepackage{tikz}
\usepackage{tikz-3dplot}
\usetikzlibrary{math}
\usepackage[active,tightpage]{preview}
\PreviewEnvironment{tikzpicture}
\setlength\PreviewBorder{1pt}
%
\begin{document}
    %
    \tdplotsetmaincoords{60}{130}
    \begin{tikzpicture}[tdplot_main_coords]
        % Parametric equations of the sphere
        \tikzmath{function equis(\r,\p,\t) {return \r * sin(\p r) * cos(\t r);};}
        \tikzmath{function ye(\r,\p,\t) {return \r * sin(\p r) * sin(\t r);};}
        \tikzmath{function zeta(\r,\p,\t) {return \r * cos(\p r);};}
        \pgfmathsetmacro{\tcero}{0.0}
        \pgfmathsetmacro{\phiInit}{0.0}
        \pgfmathsetmacro{\phiMid}{0.5*pi}
        \pgfmathsetmacro{\phiEnd}{pi}
        \pgfmathsetmacro{\thetaInit}{0.5*pi}
        \pgfmathsetmacro{\thetaMid}{1.85*pi}
        \pgfmathsetmacro{\thetaEnd}{2.5*pi}
        %
        \pgfmathsetmacro{\step}{0.02}
        \pgfmathsetmacro{\next}{\tcero+0.5*\step}
 
 
הההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההה
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX