DFT Choices

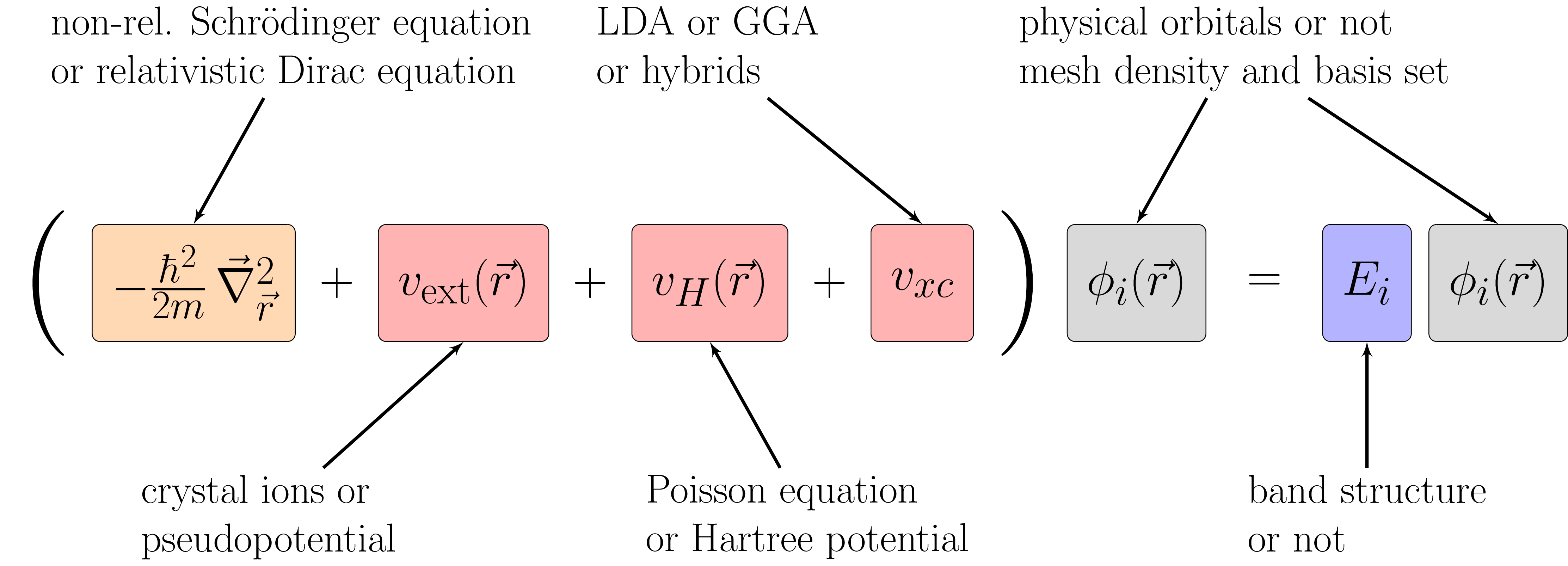
Visualization of the many choices involved in a Kohn-Sham calculation. It can be non-relativistic based on the classical Schrödinger equation or fully relativistic based on the Dirac equation which includes spin-orbit coupling. The near-core electrons can be modeled explicitly in an all-electron calculation or, much more commonly, incorporated along with the nucleus into an effective pseudo-potential. The Hartree energy can be obtained by integrating the charge density or by solving the Poisson equation. The exchange-correlation potential can be treated with a huge library of density functionals, most commonly LDA and GGA. The wave functions can be computed on a numerical mesh and expanded in one of many possible basis sets, e.g. plane waves, APW, or PAW. Inspired by https://arxiv.org/abs/cond-mat/0211443.

Edit and compile if you like:

% Visualization of the many choices involved in a Kohn-Sham calculation. It can be non-relativistic based on the classical Schrödinger equation or fully relativistic based on the Dirac equation which includes spin-orbit coupling. The near-core electrons can be modeled explicitly in an all-electron calculation or, much more commonly, incorporated along with the nucleus into an effective pseudopotential. The Hartree energy can be obtained by integrating the charge density or by solving the Poisson equation. The exchange-correlation potential can be treated with a huge library of density functionals, most commonly LDA and GGA. The wave functions can be computed on a numerical mesh and expanded in one of many possible basis sets, e.g. plane waves, APW, or PAW. Inspired by https://arxiv.org/abs/cond-mat/0211443.

\documentclass[tikz]{standalone}

\usepackage{mathtools}

\usetikzlibrary{positioning,arrows}

\begin{document}
\begin{tikzpicture}[
    g/.style={rectangle,draw,rounded corners,minimum height=6em,inner sep=1em,font=\Huge},
    w/.style={font=\Huge},
    c/.style={node distance=15ex,align=left,font=\huge},
    a/.style={draw,-latex',ultra thick}
  ]

  \node [w,scale=3] (bra) {(};
  \node [node distance=0ex,fill=orange!30,g,right=of bra] (kinetic) {$-\frac{\hbar^2}{2m}\,\vec{\nabla}_{\vec{r}}^2$};
  \node [node distance=2ex,w,right=of kinetic] (plus1) {$+$};
  \node [node distance=2ex,fill=red!30,g,right=of plus1] (external) {$v_\text{ext}(\vec{r})$};
  \node [node distance=2ex,w,right=of external] (plus2) {$+$};
  \node [node distance=2ex,fill=red!30,g,right=of plus2] (hartree) {$v_H(\vec{r})$};
  \node [node distance=2ex,w,right=of hartree] (plus3) {$+$};
  \node [node distance=2ex,fill=red!30,g,right=of plus3] (xc) {$v_{xc}$};
  \node [node distance=0ex,w,right=of xc,scale=3] (ket) {)};
  \node [node distance=0ex,fill=gray!30,g,right=of ket] (phi1) {$\phi_i(\vec{r})$};
  \node [node distance=4ex,w,right=of phi1] (equal) {$=$};
  \node [node distance=4ex,fill=blue!30,g,right=of equal] (energy) {$E_i$};
  \node [node distance=2ex,fill=gray!30,g,right=of energy] (phi2) {$\phi_i(\vec{r})$};

  \node [c,above=of kinetic,xshift=5em] (kinetic comment) {non-rel. Schrödinger equation\\or relativistic Dirac equation};
  \node [c,below=of external,xshift=-10em] (external comment) {crystal ions or\\pseudopotential};
  \node [c,below=of hartree,xshift=5em] (hartree comment) {Poisson equation\\or Hartree potential};
  \node [c,above=of xc,xshift=-11em] (xc comment) {LDA or GGA\\or hybrids};
  \node [c,above=of phi1,xshift=5em] (phi comment) {physical orbitals or not\\mesh density and basis set};
  \node [c,below=of energy] (energy comment) {band structure\\ or not};

  \path [a] (kinetic comment) -- (kinetic.north);
  \path [a] (external comment) -- (external.south);
  \path [a] (hartree comment) -- (hartree.south);
  \path [a] (xc comment) -- (xc.north);
  \path [a] (phi comment) -- (phi1.north);
  \path [a] (phi comment) -- (phi2.north);
  \path [a] (energy comment) -- (energy.south);

\end{tikzpicture}
\end{document}