Divergence of vector fields

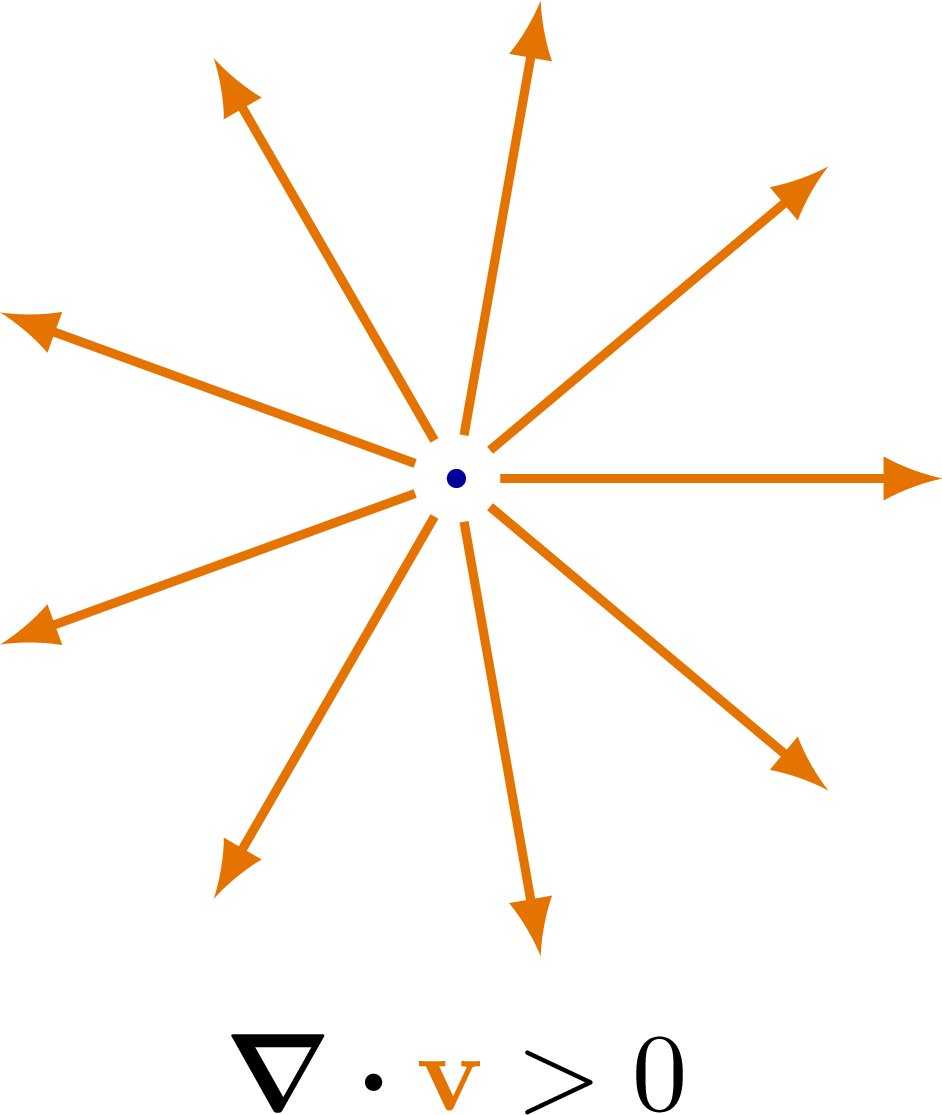
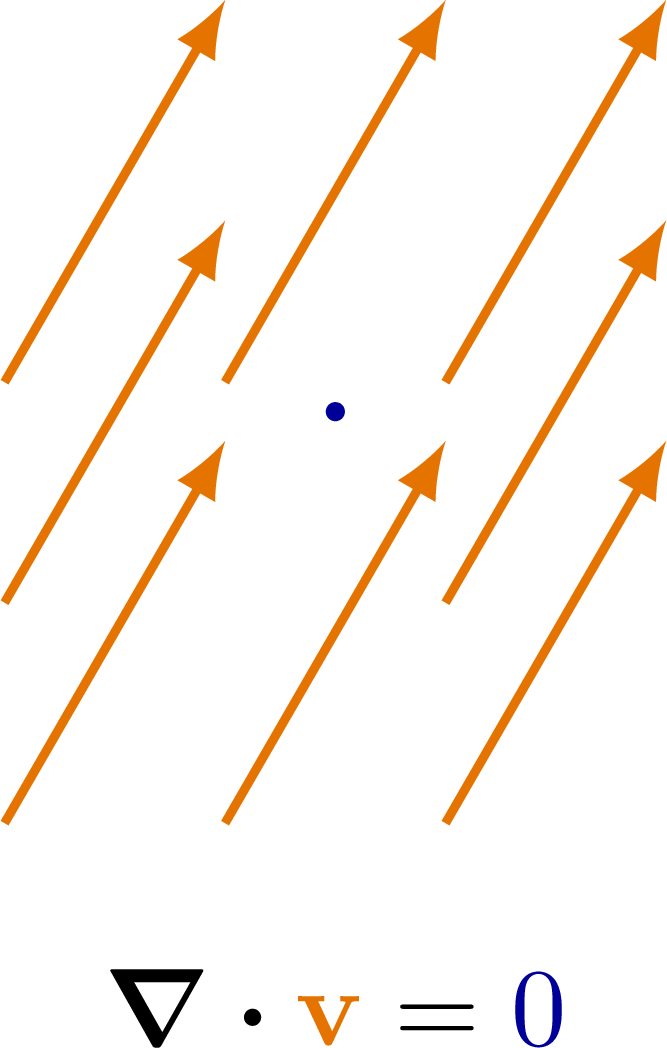
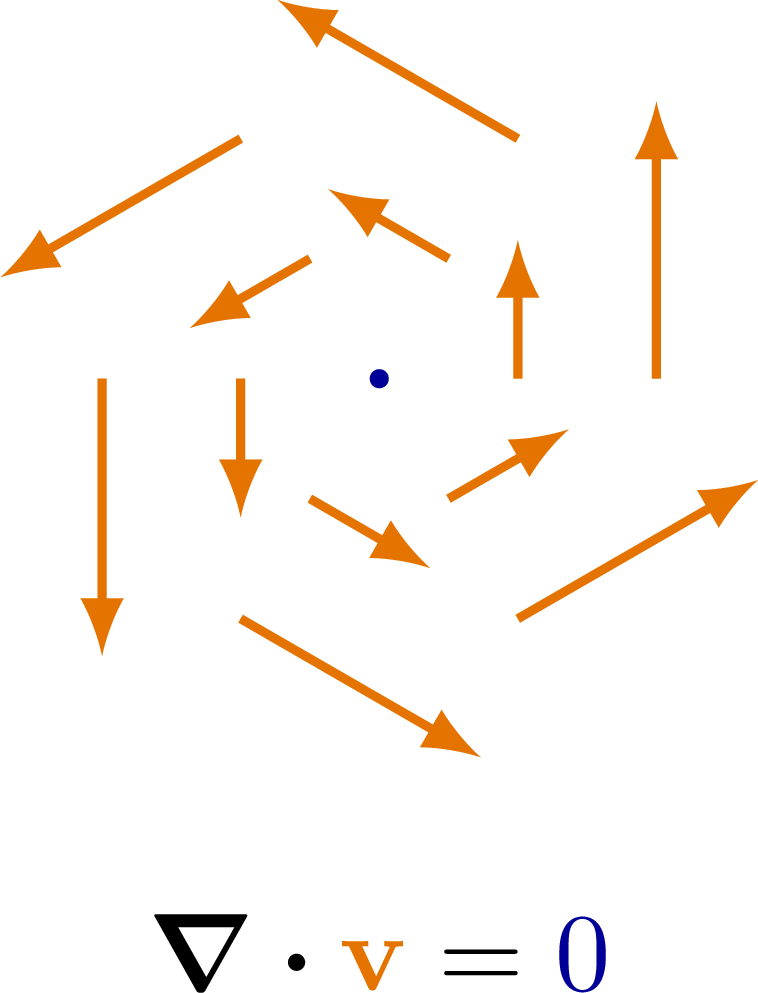
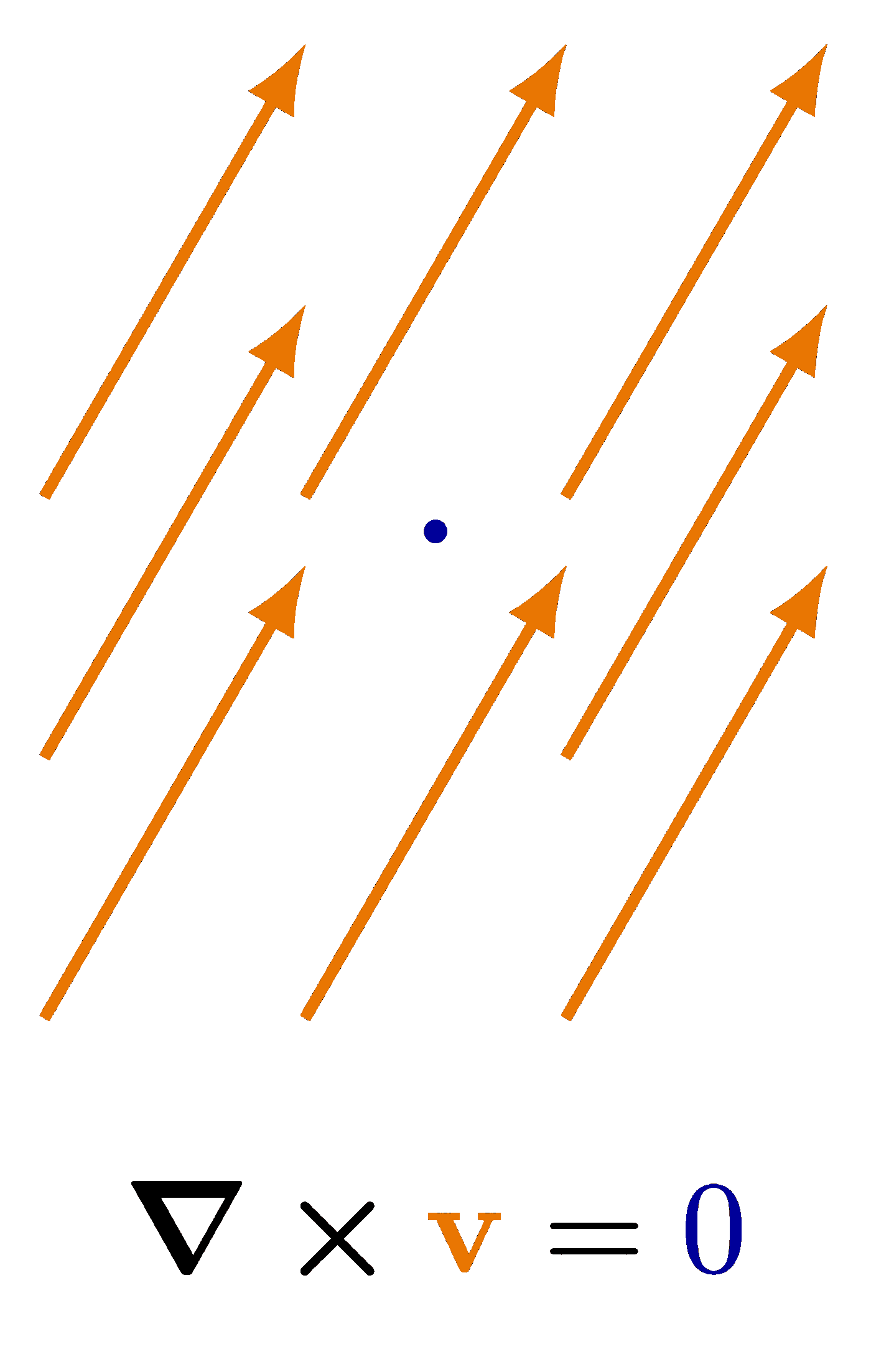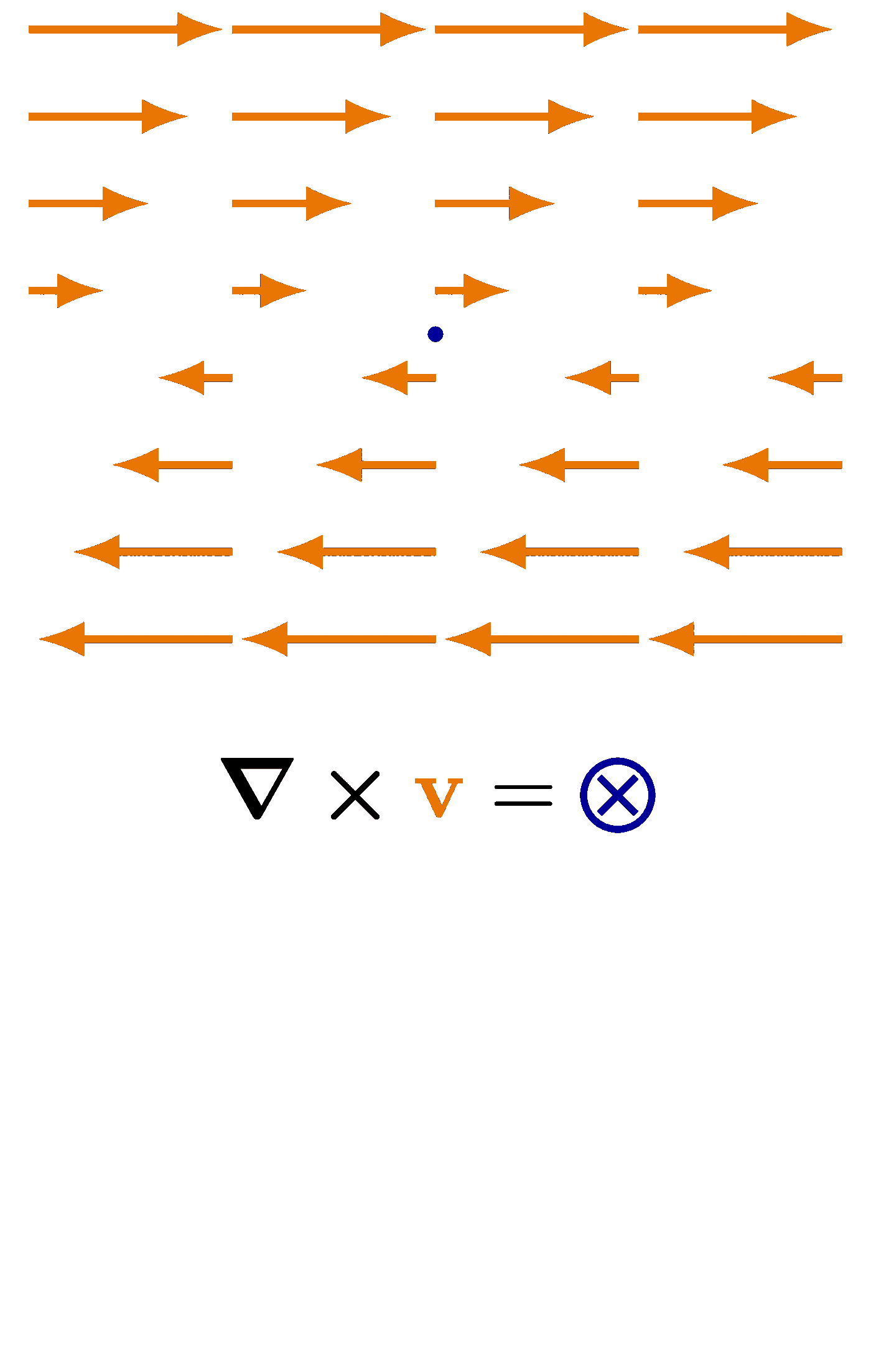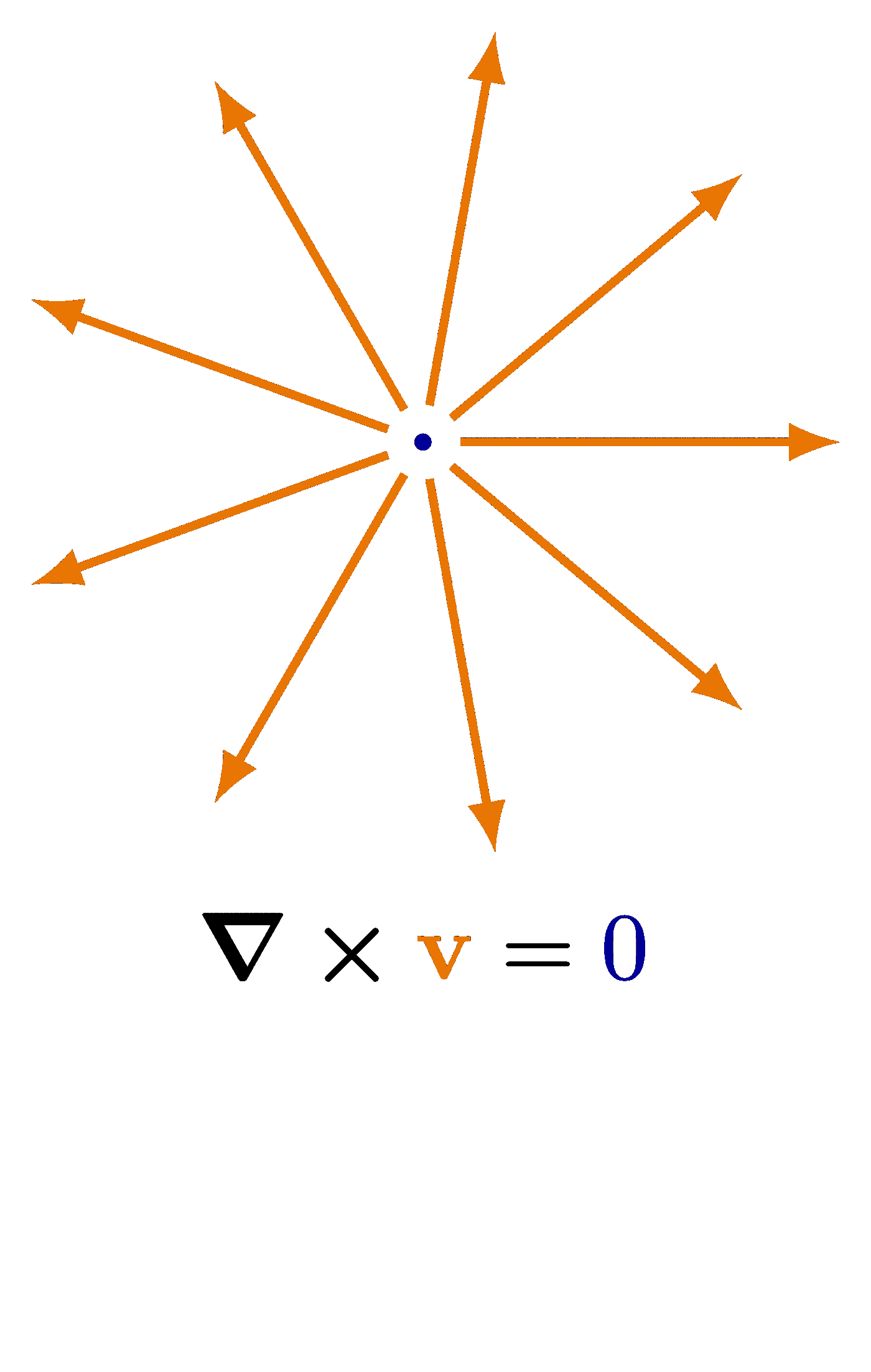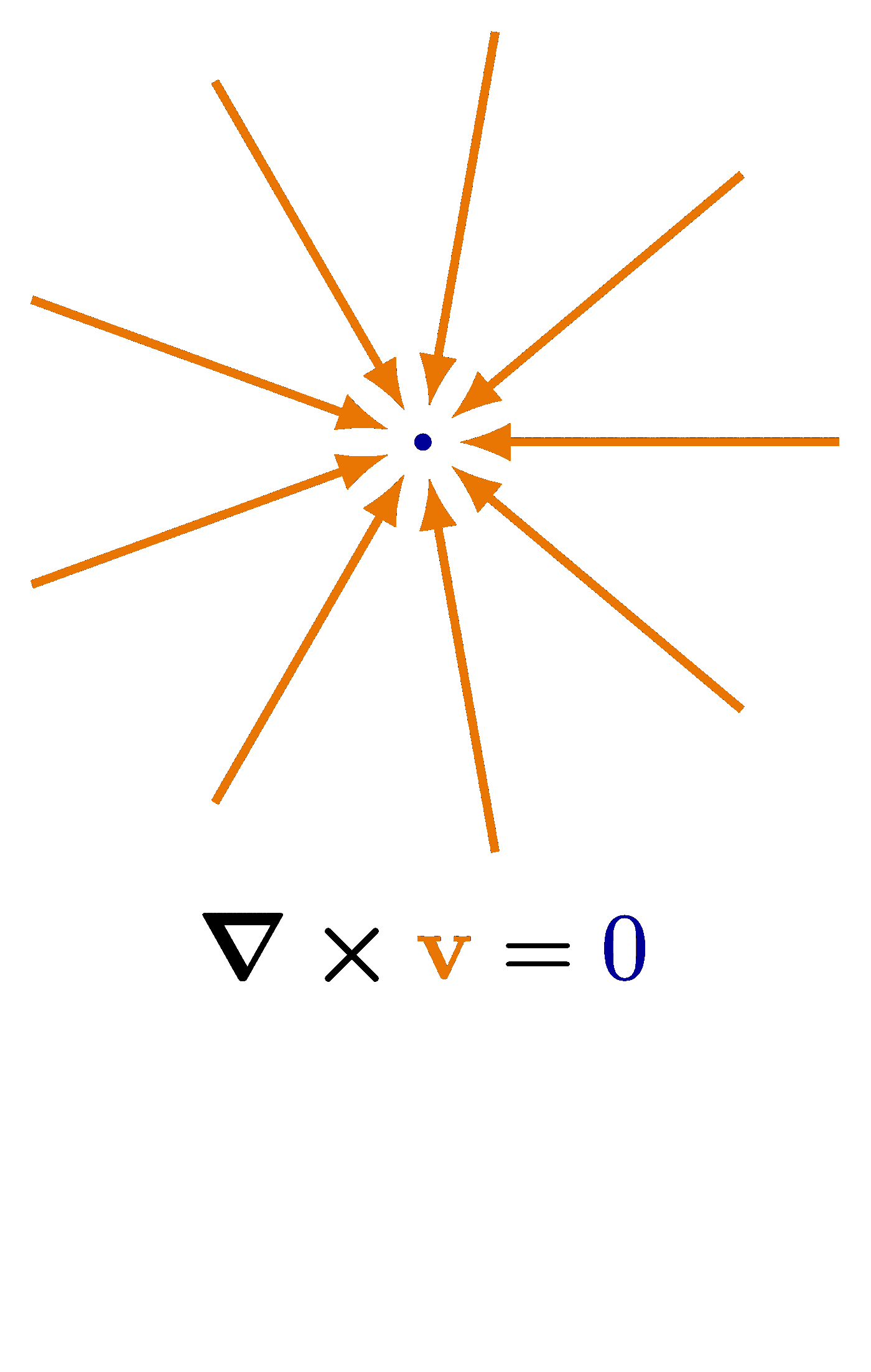
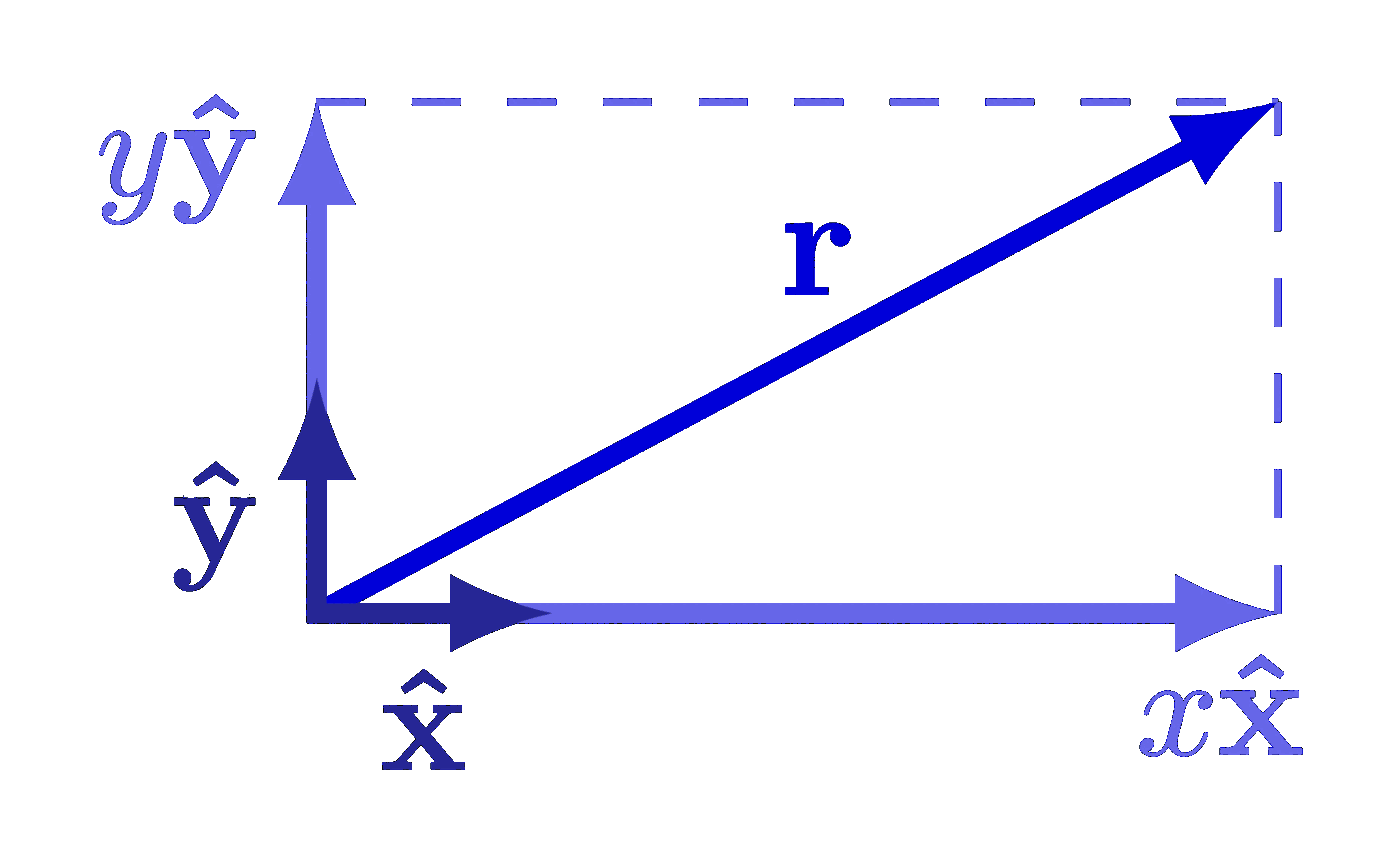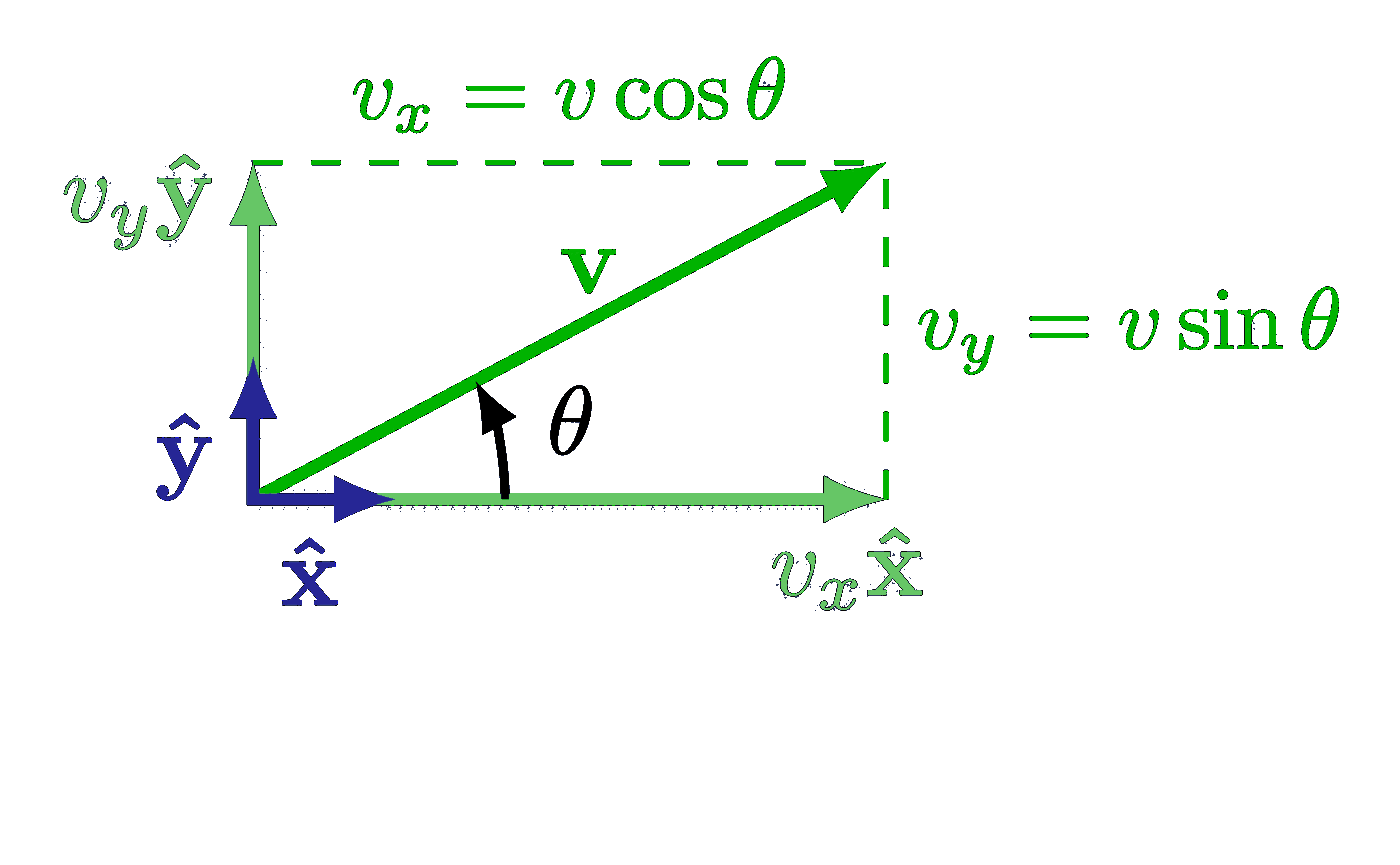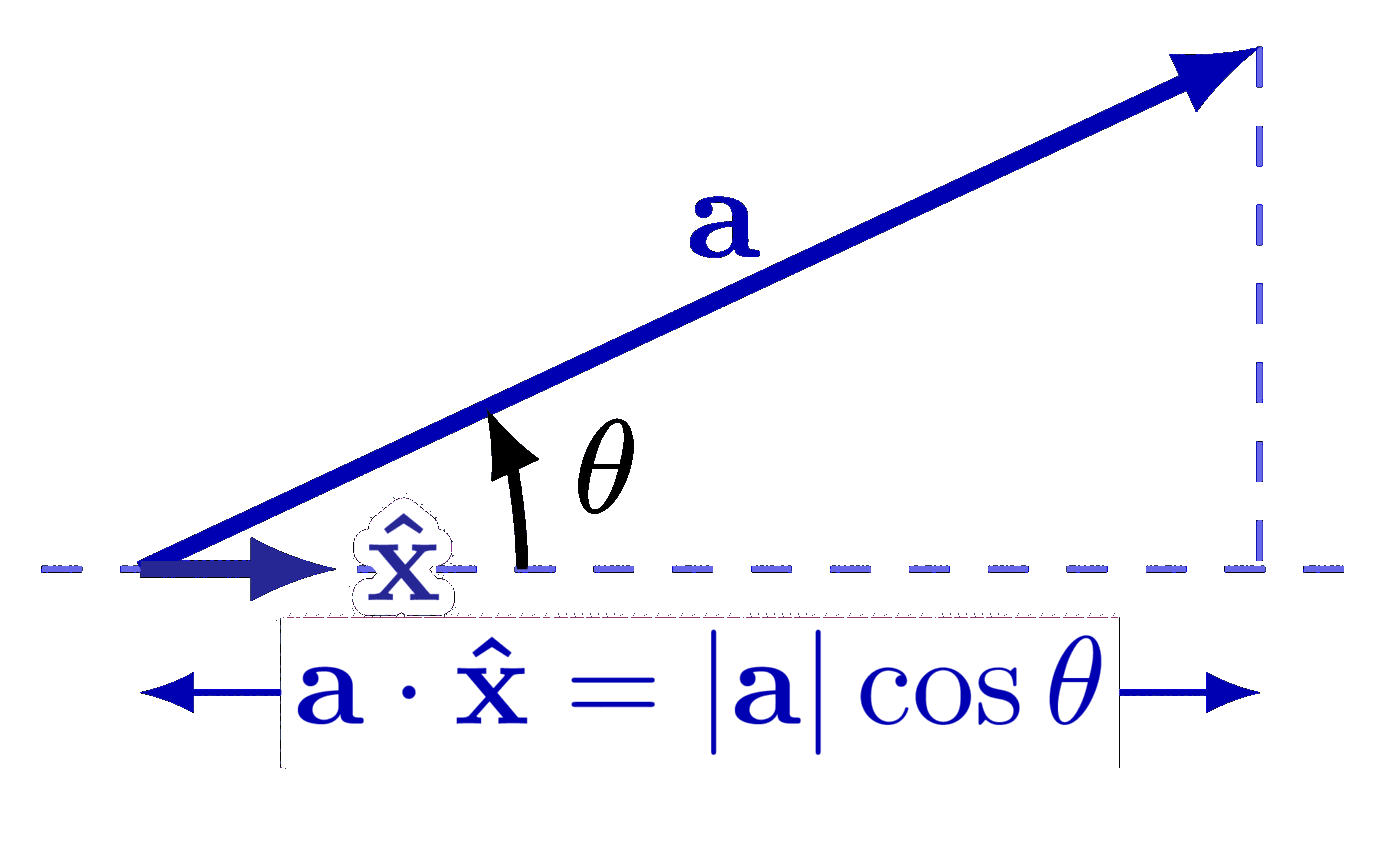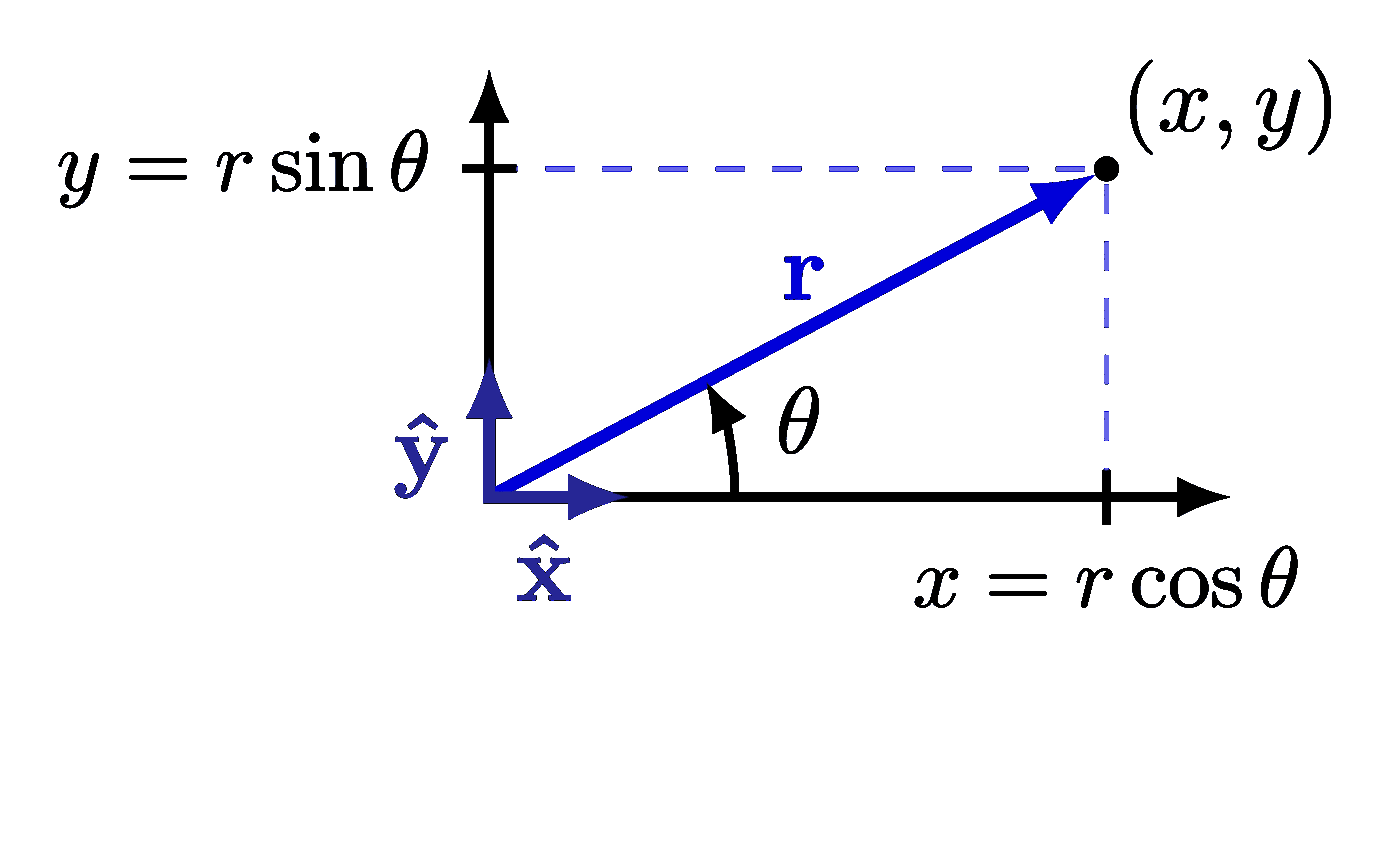
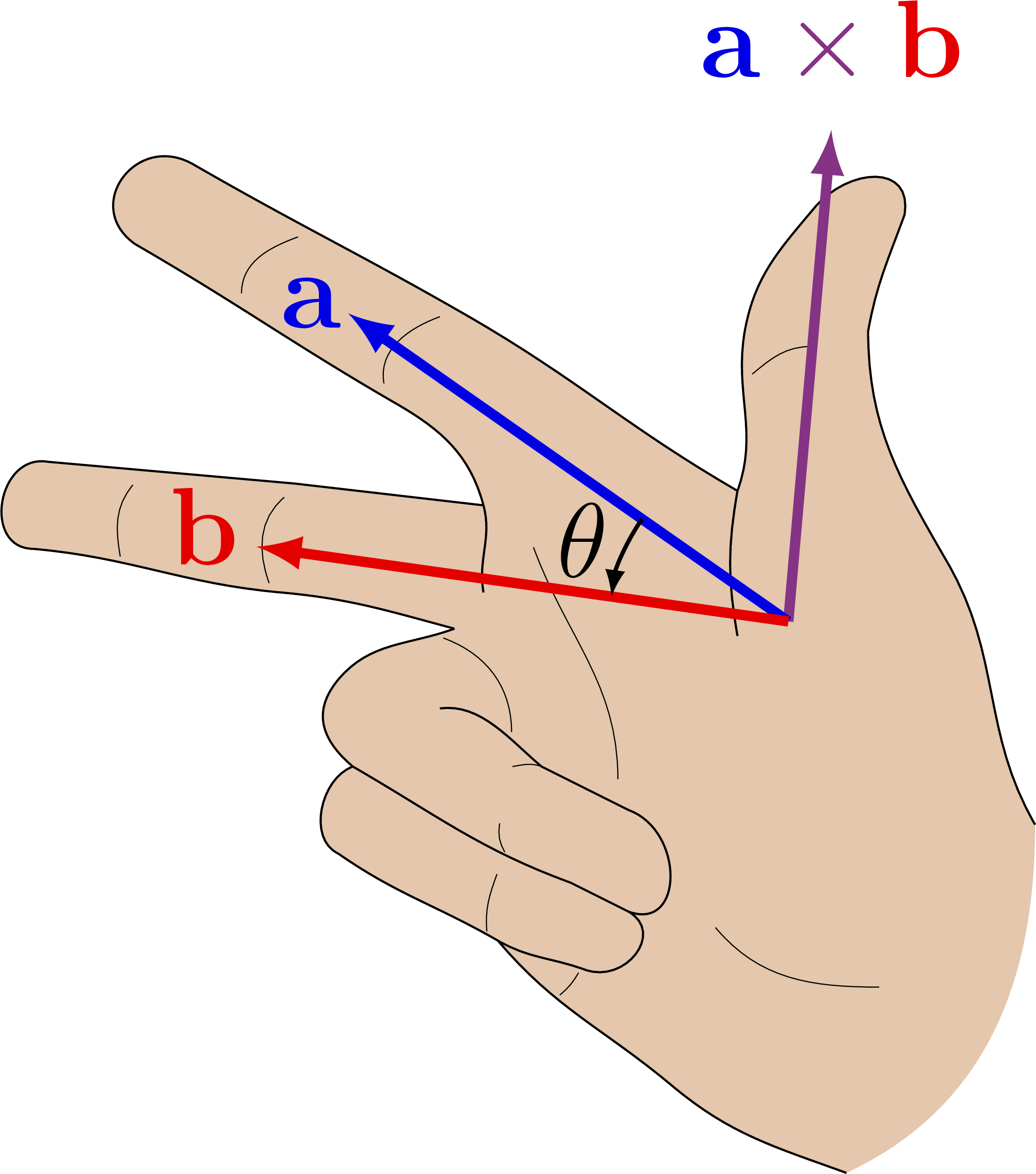
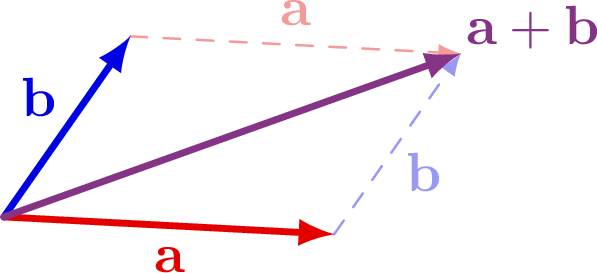
Also see the curl examples, or other figures under the “vectors” tag: the vector sum rule, scalar product, right-hand rule.

Edit and compile if you like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
% Author: Izaak Neutelings (Februari, 2020)
\documentclass[border=3pt,tikz]{standalone}
\usepackage{physics}
\usepackage{tikz}
\tikzset{>=latex} % for LaTeX arrow head
\usepackage{xcolor}
\colorlet{veccol}{orange!90!black}
\colorlet{myblue}{blue!60!black}
\tikzstyle{vector}=[->,thick,veccol]
\def\R{1.4}
\def\r{0.03}
\def\N{9}
\def\null{\color{myblue}{0}}
\begin{document}
% RADIAL OUTWARD
\begin{tikzpicture}
  \fill[myblue] (0,0) circle (\r);
  \foreach \i [evaluate={\ang=\i*360/\N;}] in {0,...,\N}{
    \draw[vector] (\ang:0.1*\R) --++ (\ang:\R);
  }
  \node at (0,-1.35*\R) {$\div{{\color{veccol}\vb{v}}} > 0$};
\end{tikzpicture}
% RADIAL INWARD
\begin{tikzpicture}
  \fill[myblue] (0,0) circle (\r);
  \foreach \i [evaluate={\ang=\i*360/\N;}] in {0,...,\N}{
    \draw[vector] (\ang:1.1*\R) -- (\ang:0.1*\R);
  }
  \node at (0,-1.35*\R) {$\div{{\color{veccol}\vb{v}}} < 0$};
\end{tikzpicture}
% ZERO
\begin{tikzpicture}
  \def\ang{60}
  \fill[myblue] (0,0) circle (\r);
 
 
הההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההה
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX