Acceleration & velocity vectors

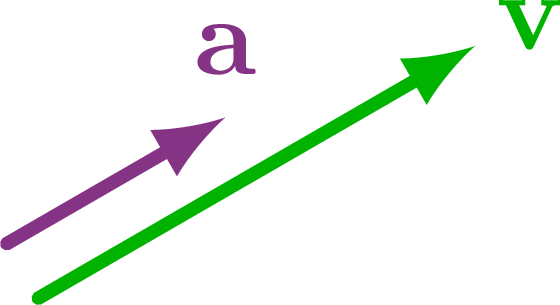
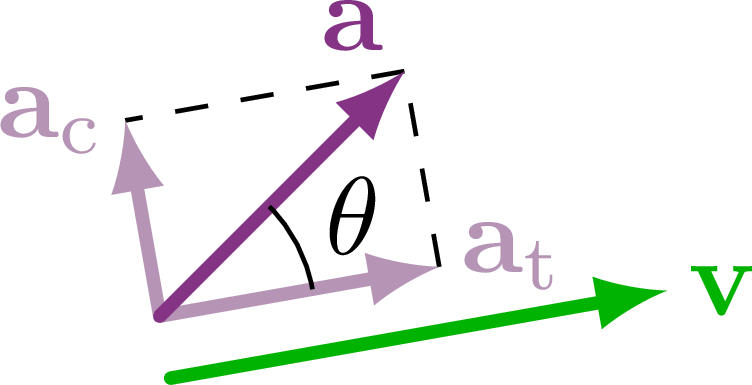
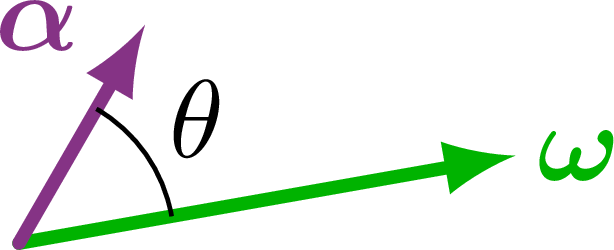Different cases of the angle between the velocity and acceleration vectors.

Also see other figures under the “vectors” tag: vector sum rule, right-hand rule, scalar production, or the divergence and curl of vector fields.

Edit and compile if you like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
% Author: Izaak Neutelings (October 2020)
\documentclass[border=3pt,tikz]{standalone}
\usepackage{physics}
\usepackage{tikz}
\usetikzlibrary{angles,quotes} % for pic
\tikzset{>=latex} % for LaTeX arrow head
\colorlet{myred}{red!65!black}
\colorlet{xcol}{blue!70!black}
\colorlet{vcol}{green!70!black}
\colorlet{acol}{red!50!blue!80!black!80}
\tikzstyle{mass}=[line width=0.6,red!30!black,fill=red!40!black!10,rounded corners=1,
                  top color=red!40!black!20,bottom color=red!40!black!10,shading angle=20]
\tikzstyle{vvec}=[->,vcol,very thick,line cap=round]
\tikzstyle{avec}=[->,acol,very thick,line cap=round]
\begin{document}
% POSITIVE ACCELERATION
\def\v{1.6}  % velocity magnitude
\def\a{0.8}  % acceleration magnitude
\def\ang{30} % angle
\begin{tikzpicture}
  \coordinate (O) at (0,0);
  \coordinate (V) at (\ang:\v);
  \coordinate (A) at (\ang:\a);
  \draw[vvec] (O)++(\ang-90:0.1) --++ (V) node[above=2,right=-2] {$\vb{v}$};
  \draw[avec] (O)++(\ang+90:0.1) --++ (A) node[above=0] {$\vb{a}$};
\end{tikzpicture}
% NEGATIVE ACCELERATION
\begin{tikzpicture}
  \coordinate (O) at (0,0);
  \coordinate (V) at (\ang:\v);
  \coordinate (A) at (\ang:\a);
  \draw[vvec] (O)++(\ang-90:0.1) --++ (V) node[above=2,right=-2] {$\vb{v}$};
  \draw[avec] (A)++(\ang+90:0.1) --++ (\ang-180:\a) node[left=-1] {$\vb{a}$};
\end{tikzpicture}
 
 
הההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההה
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX