Parallel axis theorem

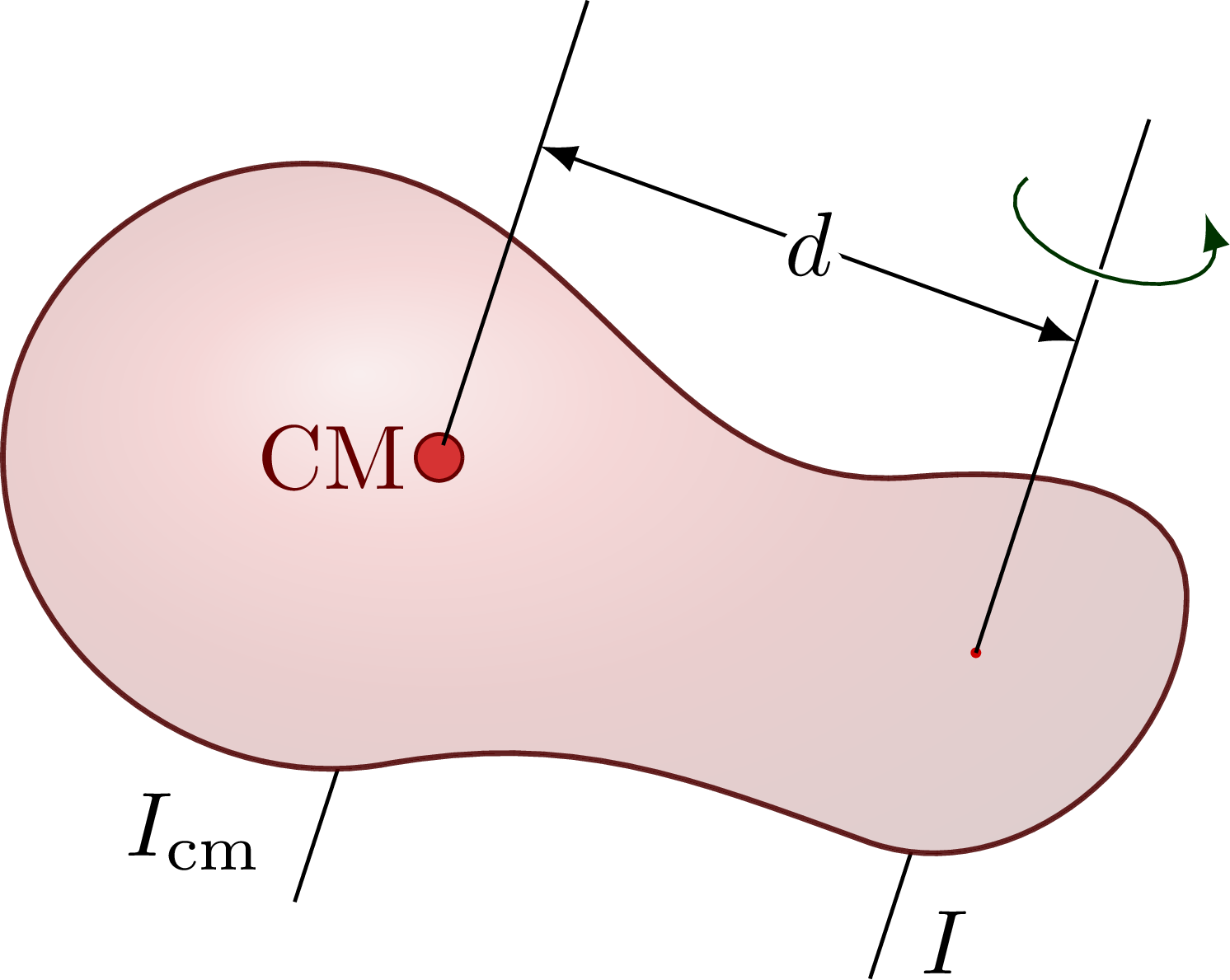
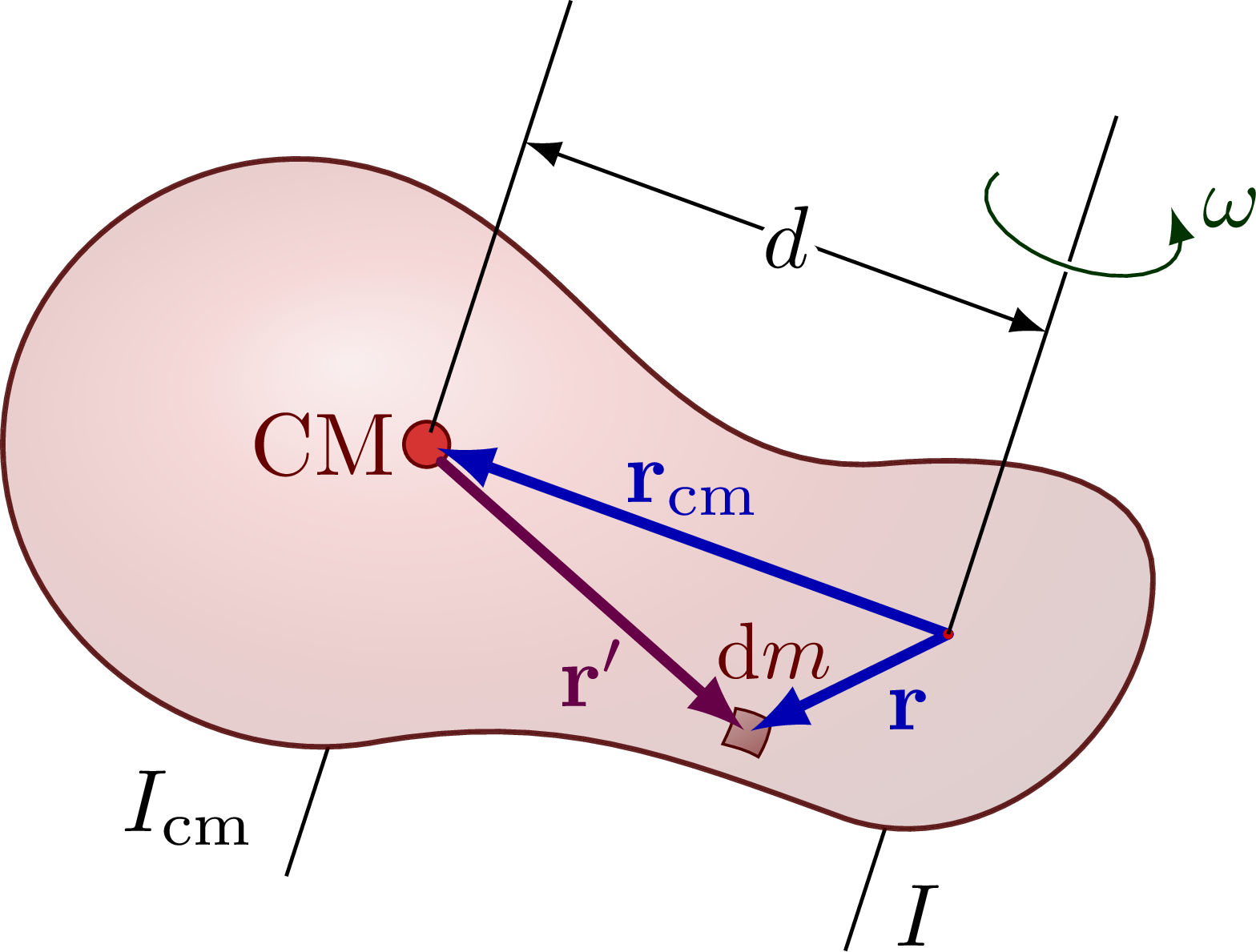
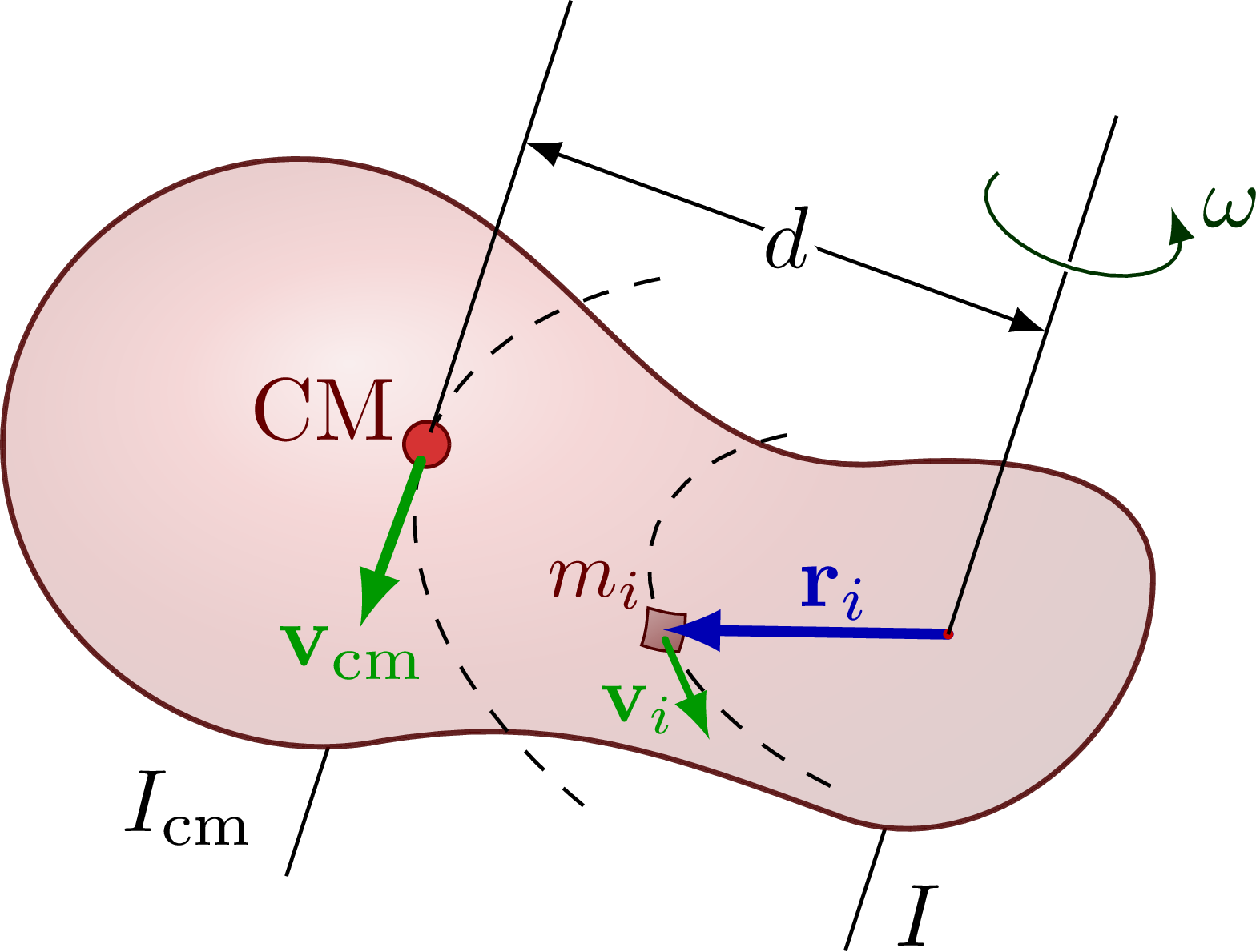
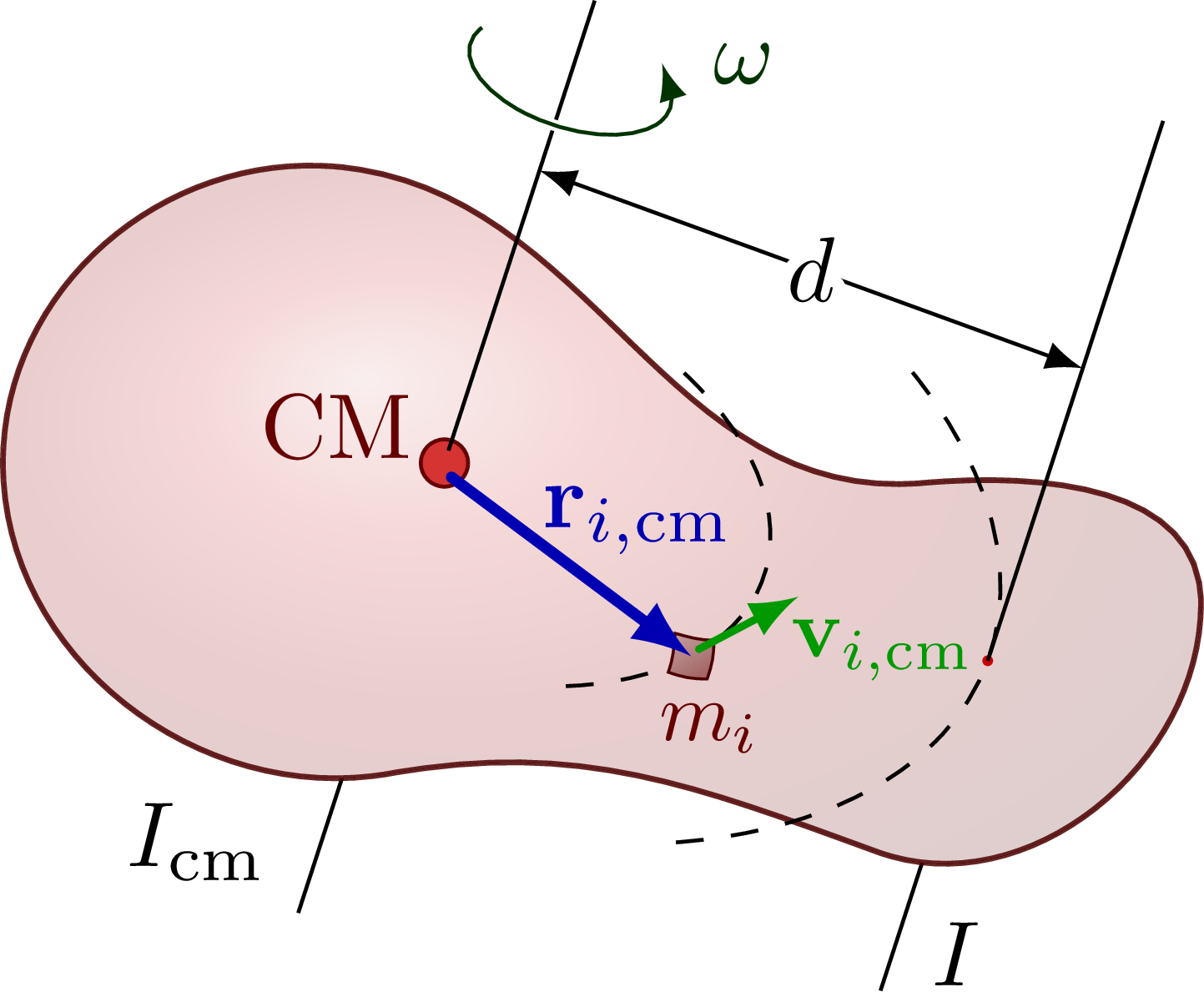
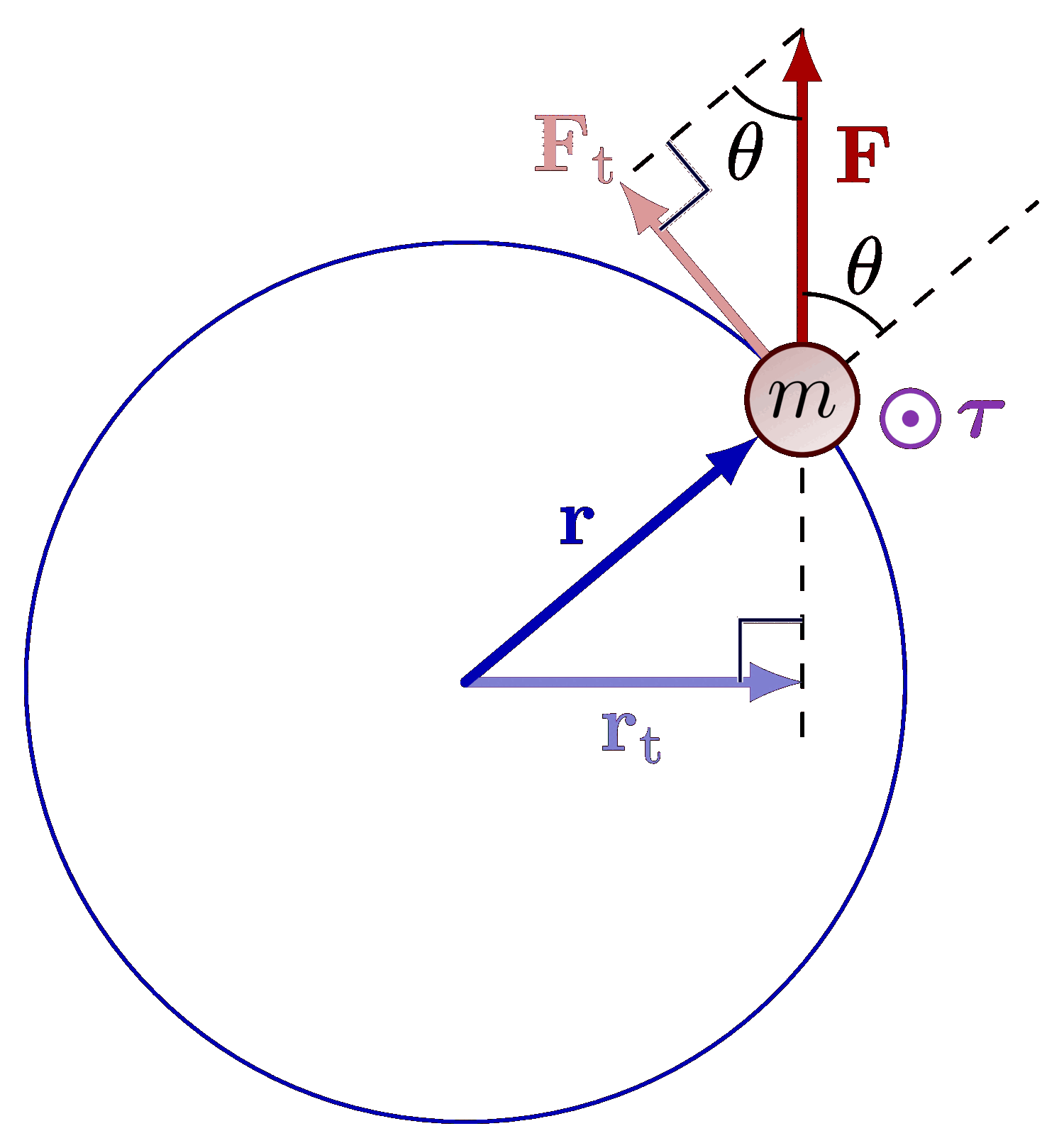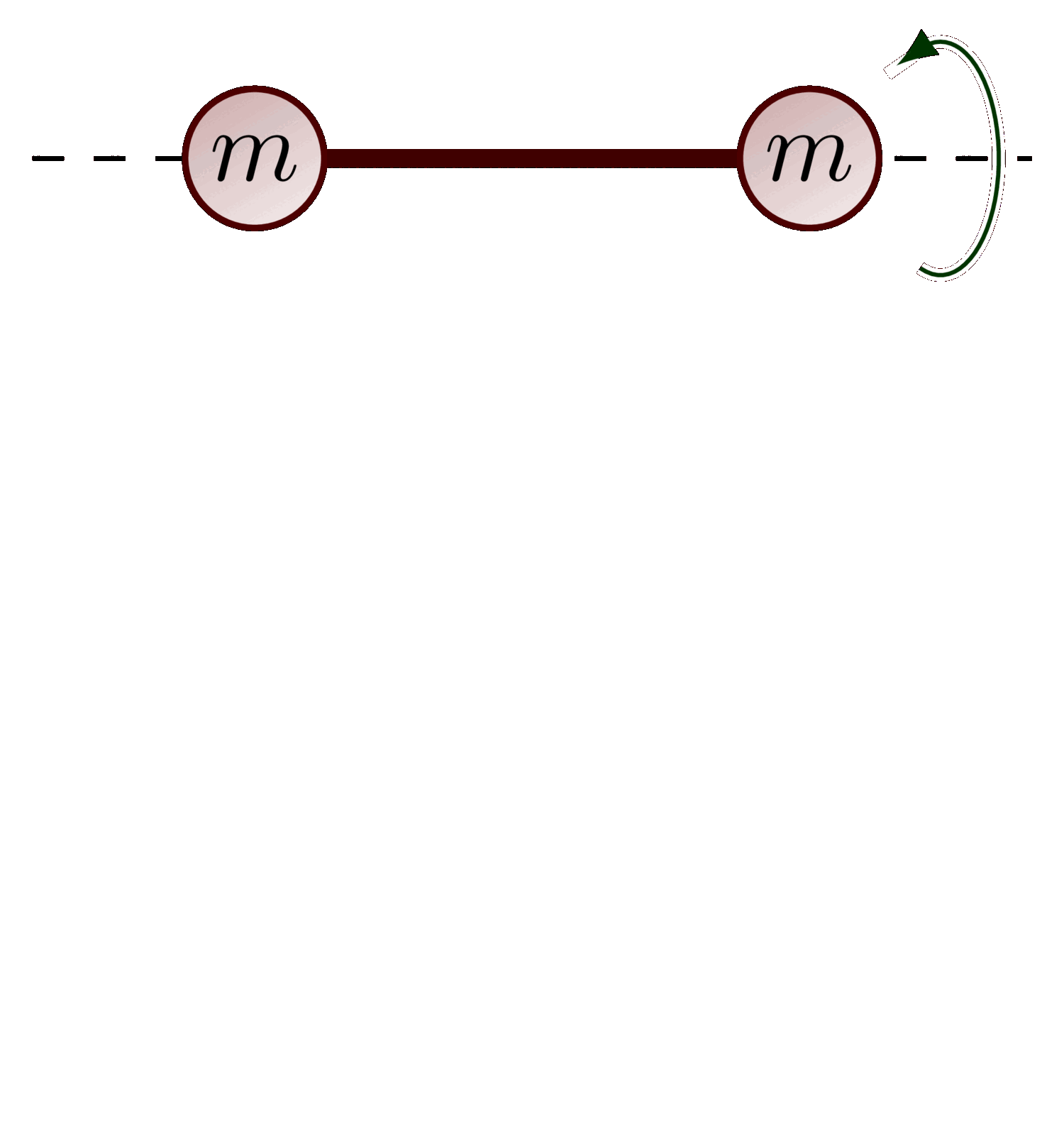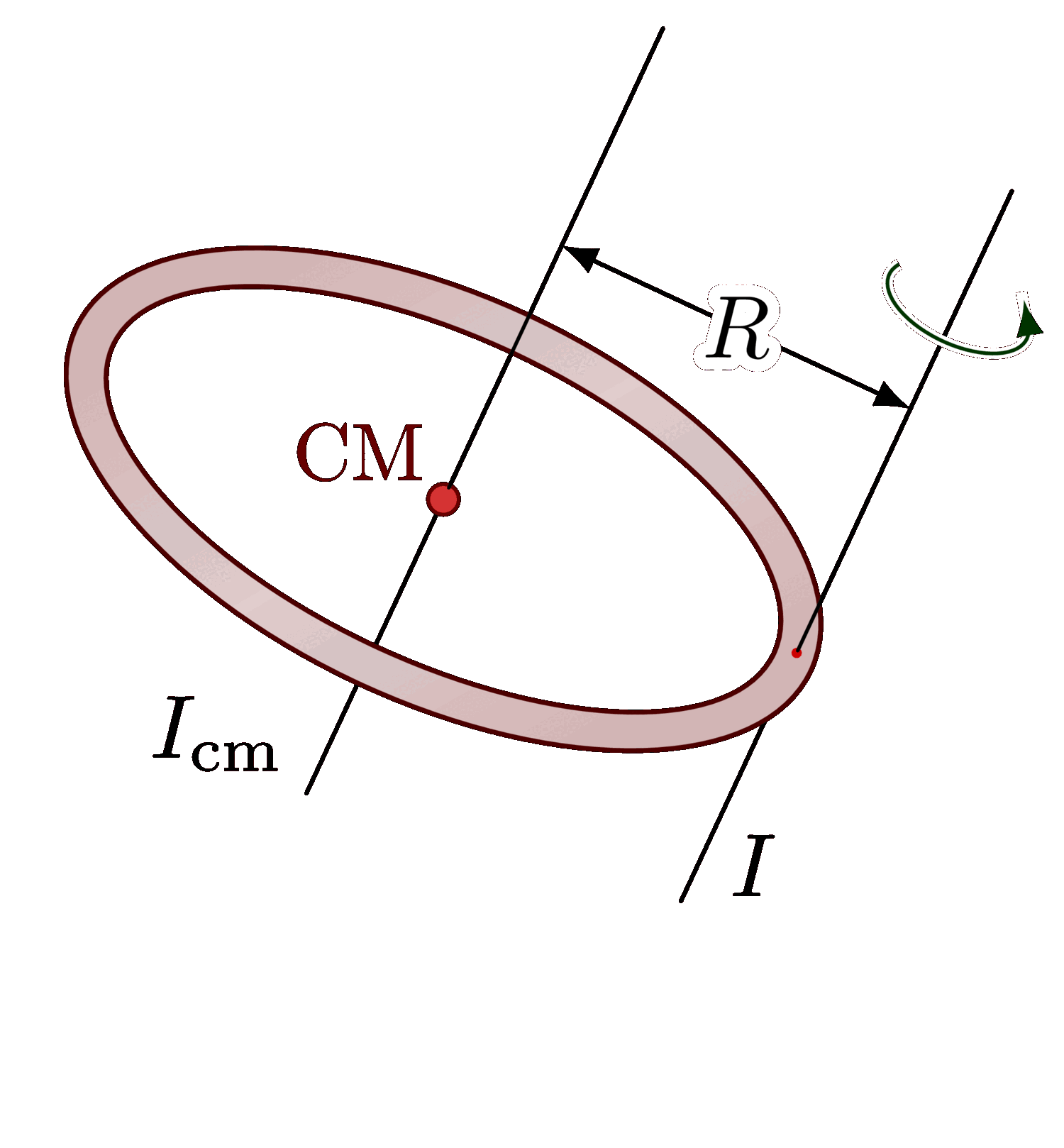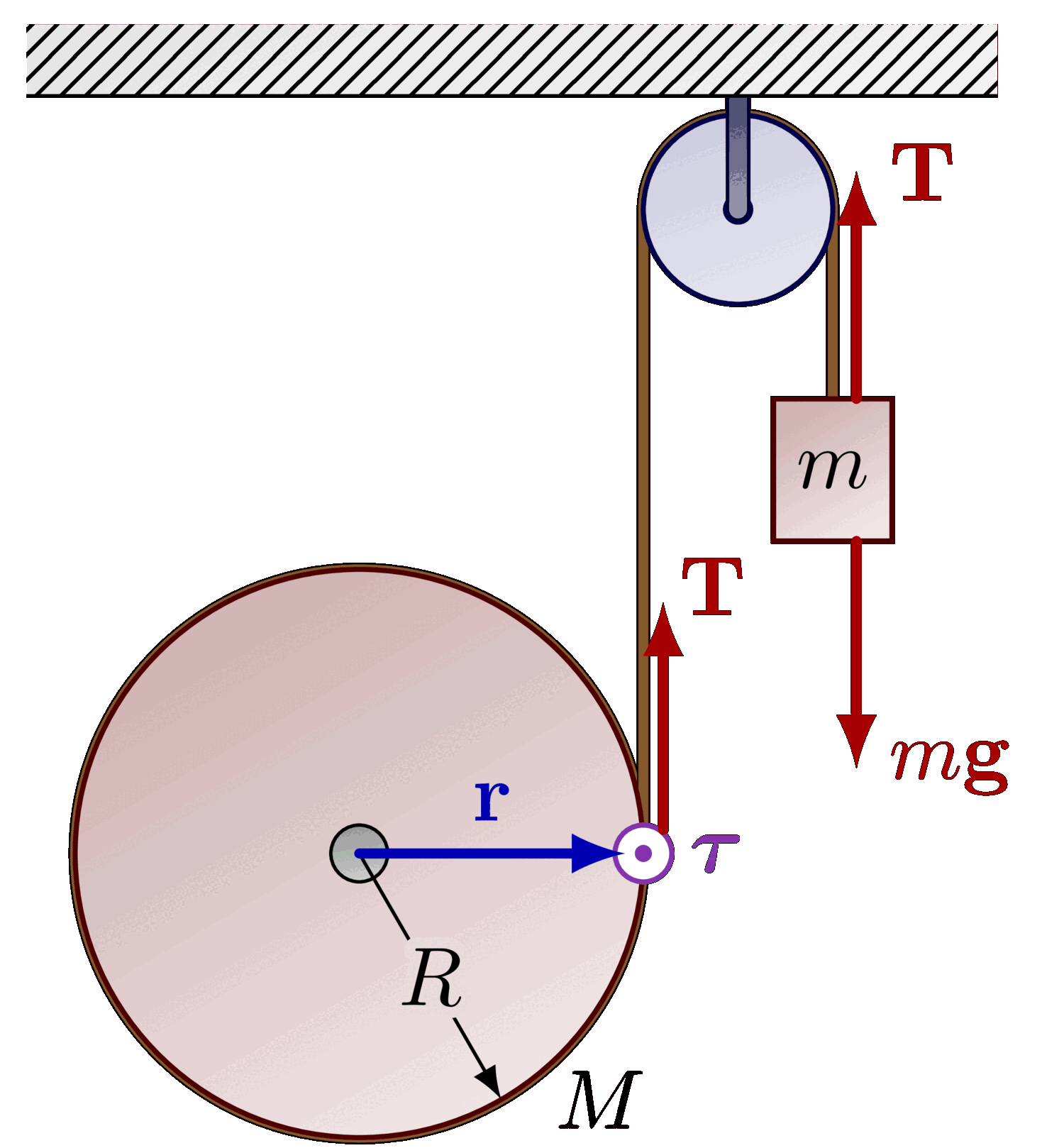
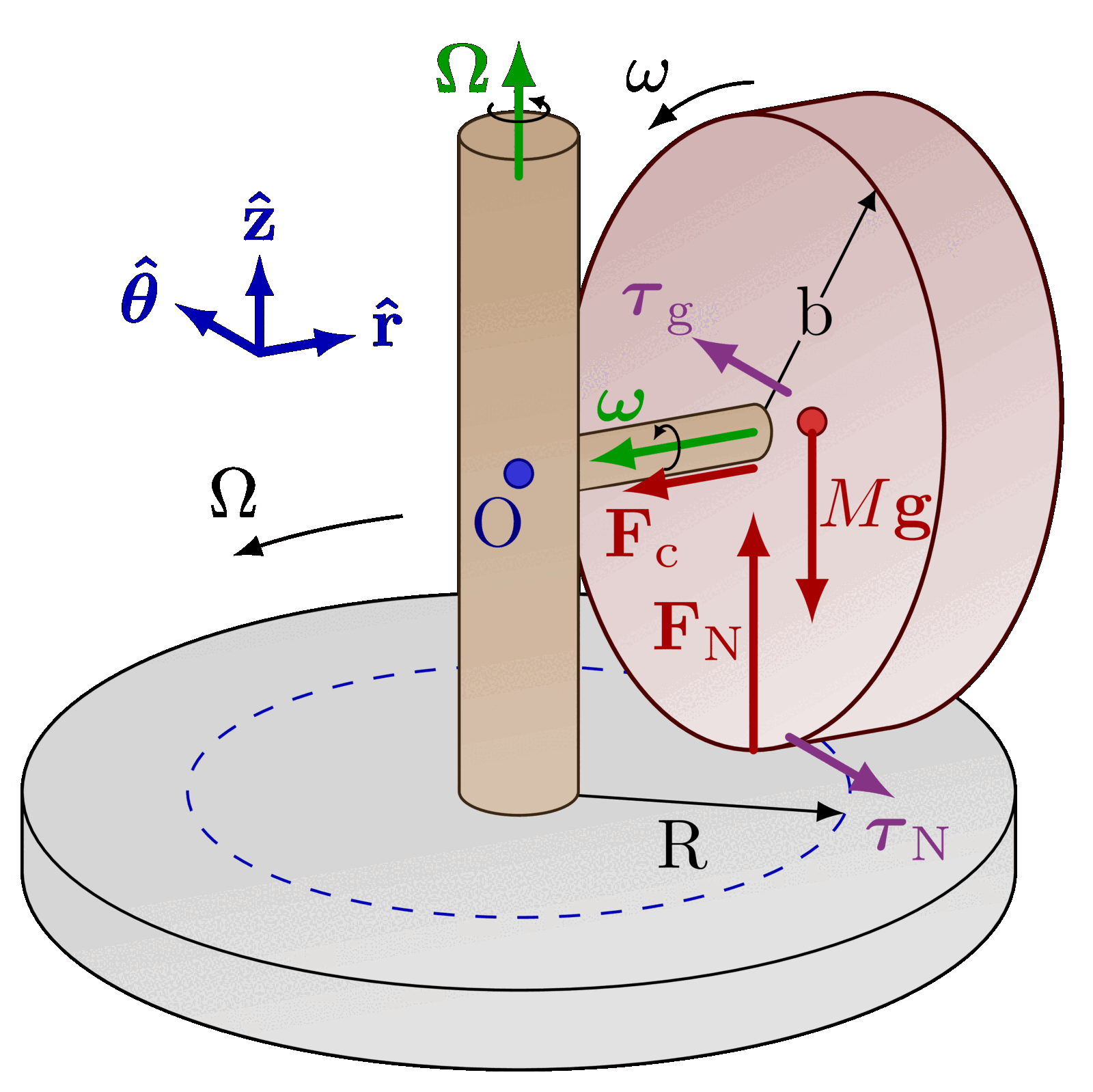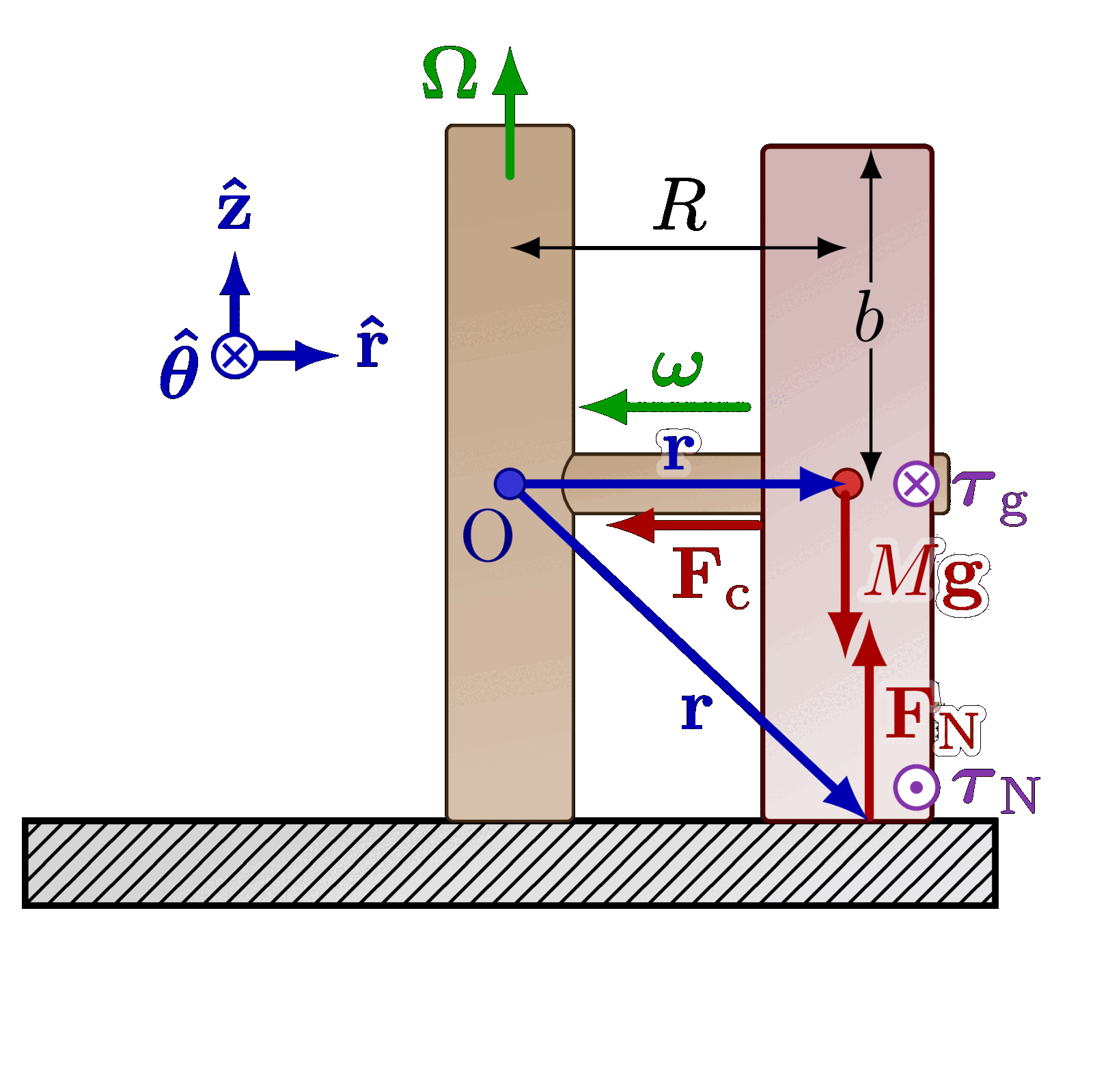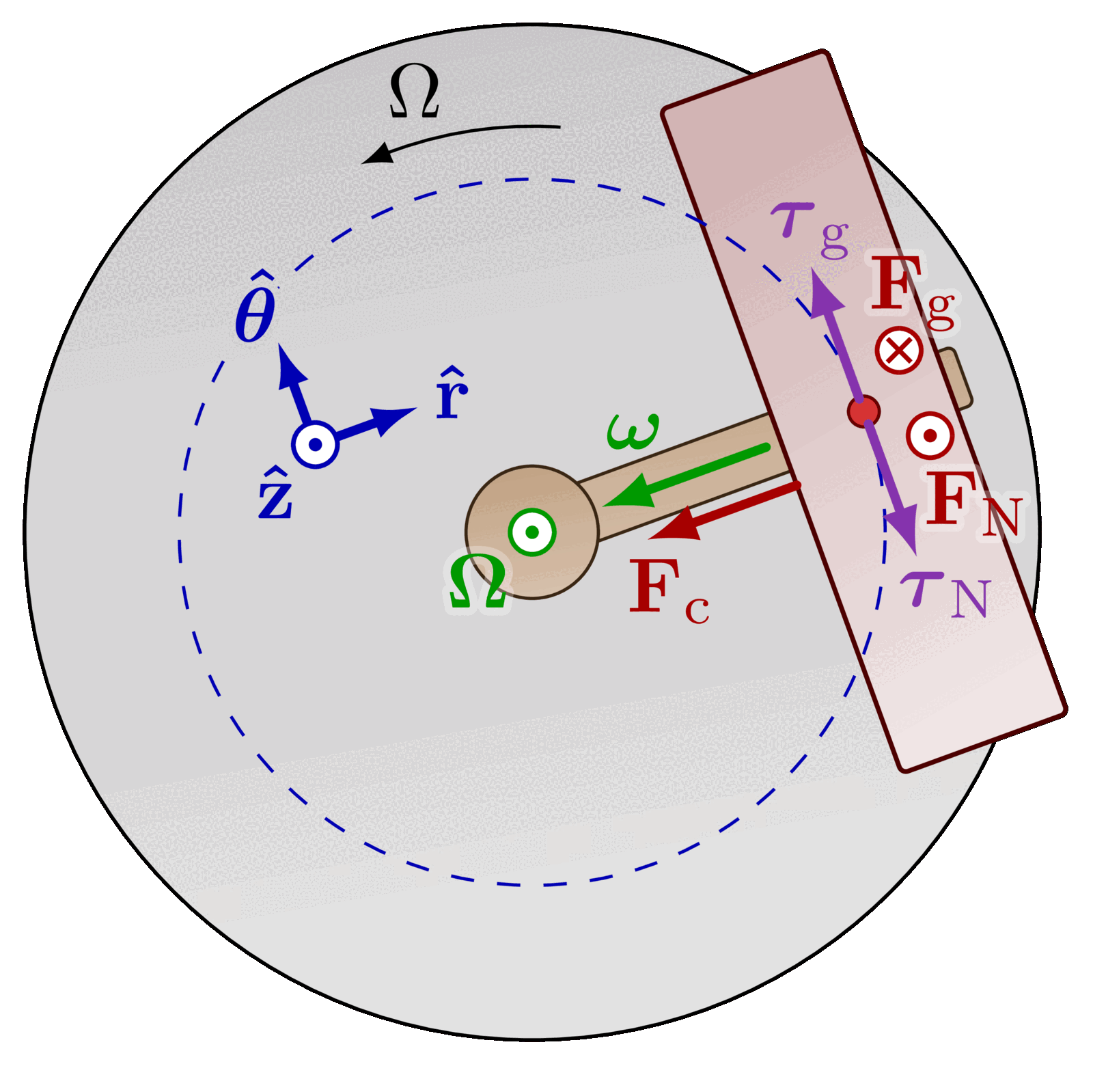
The parallel axis theorem (or Steiner’s theorem).

Edit and compile if you like:

% Author: Izaak Neutelings (August 2021)
\documentclass[border=3pt,tikz]{standalone}
\usepackage{physics}
\usepackage{tikz}
\usepackage[outline]{contour} % glow around text
\usetikzlibrary{calc}
%\usetikzlibrary{angles,quotes} % for pic
%\usetikzlibrary{arrows.meta}
%\usetikzlibrary{patterns}
\tikzset{>=latex} % for LaTeX arrow head
\contourlength{1.35pt}

\colorlet{xcol}{blue!70!black}
\colorlet{xcol'}{xcol!50!red!80!black}
\colorlet{vcol}{green!60!black}
\colorlet{myred}{red!65!black}
\colorlet{mydarkred}{red!40!black}
\colorlet{mypurple}{blue!60!red!80}
\colorlet{mydarkgreen}{green!20!black}
\tikzstyle{rvec}=[->,xcol,very thick,line cap=round]
\tikzstyle{vvec}=[->,vcol,very thick,line cap=round]
\tikzstyle{CM}=[mydarkred,fill=red!80!black!80]
\tikzstyle{mass}=[line width=0.6,draw=red!30!black, %rounded corners=1,
                  top color=mydarkred!30,bottom color=mydarkred!10,shading angle=30]
\tikzstyle{dark mass}=[line width=0.3,red!30!black, %rounded corners=1,
                       top color=mydarkred!40,bottom color=mydarkred!60,shading angle=30]

\def\r{0.05} % pulley small radius
\tikzset{
  pics/rotarr/.style={
    code={
      \draw[white,very thick] ({#1*cos(200)},0) arc(-200:30:{#1} and {#1/2}) --++ (125:0.1);
      \draw[->,mydarkgreen] ({#1*cos(200)},0) coordinate (W1) arc(-200:20:{#1} and {#1/2}) node[midway] (W2) {} --++ (125:0.1) coordinate (W3);
  }},
  pics/rotarr/.default=0.4,
}


\begin{document}


% PARALLEL AXIS (STEINER'S) THEOREM
\def\L{1.2}    % size scale
\def\A{1.8}    % height axis above body
\def\d{2.2}    % distance parallel axis to CM
\def\ang{-20}  % angle connection between axes
\def\anga{72}  % angle axes
\def\bodyshape{
  (-100:1.0*\L) to[out=190,in=-90]
  (180:1.4*\L) to[out=90,in=175]
  (110:1.0*\L) to[out=-5,in=185]
  ($(R)+(110:0.6*\L)$) to[out=5,in=90]
  ($(R)+(15:0.7*\L)$) to[out=-90,in=-20]
  ($(R)+(-120:0.7*\L)$) to[out=160,in=10] cycle
}
\def\body{ % shape
  \fill[ball color=red!80!black] \bodyshape;
  \draw[line width=0.6,draw=red!30!black,fill=red!60!black!5,fill opacity=0.85]
    \bodyshape;
  %\fill[mass] \bodyshape;
}
\begin{tikzpicture}
  \coordinate (M) at (0,0); % center of mass
  \coordinate (R) at (\ang:\d); % intersection with new axis
  \draw (M) --++ (\anga-180:1.5*\L) node[above left] {$I_\text{cm}$}; % axis below
  \draw (R) --++ (\anga-180:1.1*\L) node[above=4,right=2] {$I$}; % axis below
  \body
  \draw[CM] (M) circle(0.09) node[left] {CM}; % center of mass point
  \fill[red!80!black] (R) circle(0.02);
  \draw (M)++(\anga:0.05) --++ (\anga:\A); % axis above
  \draw (R) --++ (\anga:1.2*\A); % axis above
  \pic[rotate=\anga-90] at ($(R)+(\anga:\A)$) {rotarr}; % rotation arrow
  %\node[mydarkgreen,right=0] at (W3) {$\omega$};
  \draw[<->] (\anga:0.7*\A) --++ (\ang:\d) % distance/radius R
    node[pos=0.5] {\contour{white}{$d$}};
\end{tikzpicture}


% PARALLEL AXIS (STEINER'S) THEOREM - derivation with position vector
\def\ys{0.6}     % vertical minor axis ellipse
\def\ri{0.56*\d} % small mass m_i distance from axis
\def\angi{210}   % small mass m_i polar angle
\def\dx{0.15}    % size small mass m_i
\def\massi{
  \draw[dark mass,rotate=\ang+\angi+30] % mass m_i
    (Ri)++(-45:{\dx/sqrt(2)}) to[out=95,in=-100]++
    (90:\dx) to[out=170,in=10]++
    (180:\dx) to[out=-100,in=100]++
    (-90:\dx) to[out=10,in=175]++ (0:\dx) -- cycle;
}
\begin{tikzpicture}
  \def\angi{240}                 % small mass m_i polar angle
  \coordinate (M) at (0,0);      % center of mass
  \coordinate (R) at (\ang:\d);  % intersection with new axis
  \path[rotate around={\ang:(R)}]
    (R) --++ (\angi:{\ri} and {\ys*\ri}) coordinate(Ri); % small mass m_i
  
  % BODY
  \draw (M) --++ (\anga-180:1.5*\L) node[above left] {$I_\text{cm}$}; % axis below
  \draw (R) --++ (\anga-180:1.1*\L) node[above=4,right=2] {$I$}; % axis below
  \body
  
  % CENTER OF MASS & MASS i
  \draw[CM] (M) circle(0.09) node[above=0,left] {CM}; % center of mass point
  \massi
  \node[mydarkred,right=3,above=3,scale=0.9] at (Ri) {$\dd{m}$};
  
  % VECTORS
  \draw[rvec] (R) -- ($(R)!0.98!(Ri)$) node[pos=0.4,below right=-2] {$\vb{r}$};
  \draw[rvec] (R) -- ($(R)!0.98!(M)$) node[pos=0.5,above=-1] {$\vb{r}_{\text{cm}}$};
  \draw[rvec,xcol'] (M)++(-50:0.09) -- ($(M)!0.99!(Ri)$) node[pos=0.5,below=1] {$\vb{r}'$};
  
  % AXES
  \fill[red!80!black] (R) circle(0.02);
  \draw (M)++(\anga:0.05) --++ (\anga:\A); % axis above
  \draw (R) --++ (\anga:1.2*\A); % axis above
  \pic[rotate=\anga-90] at ($(R)+(\anga:\A)$) {rotarr}; % rotation arrow
  \node[mydarkgreen,right=0] at (W3) {$\omega$};
  \draw[<->] (\anga:0.7*\A) --++ (\ang:\d) % distance/radius R
    node[pos=0.5] {\contour{white}{$d$}};
  
\end{tikzpicture}


% PARALLEL AXIS (STEINER'S) THEOREM - derivation with velocity
\def\massi{
  \draw[dark mass,rotate=\ang+\angi-20] % mass m_i
    (Ri)++(-45:{\dx/sqrt(2)}) to[out=95,in=-100]++
    (90:\dx) to[out=170,in=10]++
    (180:\dx) to[out=-100,in=100]++
    (-90:\dx) to[out=10,in=175]++ (0:\dx) -- cycle;
}
\begin{tikzpicture}
  \coordinate (M) at (0,0);      % center of mass
  \coordinate (R) at (\ang:\d);  % intersection with new axis
  \path[rotate around={\ang:(R)}]
    (R) --++ (\angi:{\ri} and {\ys*\ri}) coordinate(Ri); % small mass m_i
  
  % BODY
  \draw (M) --++ (\anga-180:1.5*\L) node[above left] {$I_\text{cm}$}; % axis below
  \draw (R) --++ (\anga-180:1.1*\L) node[above=4,right=2] {$I$}; % axis below
  \body
  
  % CENTER OF MASS
  \draw[dashed,rotate around={\ang:(R)}] % rotation ellipse through CM
    (R)++(135:{\d} and {\ys*\d}) arc(135:240:{\d} and {\ys*\d});
  \draw[CM] (M) circle(0.09) node[above=4,left] {CM}; % center of mass point
  \draw[vvec] (M)++(\ang-90:0.07) --++ (\ang-90:0.7) % velocity center of mass
    node[left=1,below=-4] {$\vb{v}_\text{cm}$};
  
  % SMALL MASS m_i
  \draw[dashed,rotate around={\ang:(R)}] % rotation ellipse through CM
    (R)++(135:{\ri} and {\ys*\ri}) arc(135:260:{\ri} and {\ys*\ri});
  \massi
  \node[mydarkred,above=5,left=-1,scale=0.9] at (Ri) {$m_i$};
  \draw[vvec,line width=0.8,rotate around={\ang:(R)}]
    (Ri)++(\angi+90:0.04) --++ (\angi+90:{0.6} and {\ys*0.6}) % velocity mass m_i
    node[pos=0.7,left=-1,scale=0.9] {$\vb{v}_i$};
  \draw[rvec] (R) -- (Ri) node[pos=0.4,above=-2.5] {$\vb{r}_i$};
  
  % AXES
  \fill[red!80!black] (R) circle(0.02);
  \draw (M)++(\anga:0.05) --++ (\anga:\A); % axis above
  \draw (R) --++ (\anga:1.2*\A); % axis above
  \pic[rotate=\anga-90] at ($(R)+(\anga:\A)$) {rotarr}; % rotation arrow
  \node[mydarkgreen,right=0] at (W3) {$\omega$};
  \draw[<->] (\anga:0.7*\A) --++ (\ang:\d) % distance/radius R
    node[pos=0.5] {\contour{white}{$d$}};
  
\end{tikzpicture}


% PARALLEL AXIS (STEINER'S) THEOREM - derivation with velocity (CM frame)
\begin{tikzpicture}
  \def\ricm{sqrt(\d*\d-2*\d*\ri*cos(\angi-180)+\ri*\ri)} % distance to mass i from CM
  \def\angicm{atan2(\ri*sin(\angi-180),\ri*cos(\angi-180)-\d)} % distance to mass i from CM
  \coordinate (M) at (0,0);      % center of mass
  \coordinate (R) at (\ang:\d);  % intersection with new axis
  \path[rotate around={\ang:(R)}]
    (R) --++ (\angi:{\ri} and {\ys*\ri}) coordinate(Ri); % small mass m_i
  
  % BODY
  \draw (M) --++ (\anga-180:1.5*\L) node[above left] {$I_\text{cm}$}; % axis below
  \draw (R) --++ (\anga-180:1.1*\L) node[above=4,right=2] {$I$}; % axis below
  \body
  
  % CENTER OF MASS
  \draw[dashed,rotate=\ang] % rotation ellipse through CM
    (45:{\d} and {\ys*\d}) arc(45:-55:{\d} and {\ys*\d});
  \draw[CM] (M) circle(0.09) node[above=4,left] {CM}; % center of mass point
  
  % SMALL MASS m_i
  \draw[dashed,rotate=\ang] % rotation ellipse through R
    (55:{\ricm} and {\ys*\ricm}) arc(55:-60:{\ricm} and {\ys*\ricm});
  \massi
  \node[mydarkred,right=2,below=2,scale=0.9] at (Ri) {$m_i$};
  \draw[vvec,line width=0.8,rotate=\ang]
    (Ri)++({\angicm-90}:0.04) --++ ({\angicm-90}:{0.6} and {\ys*0.6}) % velocity mass m_i
    node[pos=0.8,below right=-2,scale=0.9] {$\vb{v}_{i,\text{cm}}$};
  \draw[rvec] (M)++({145+\angicm}:0.06) -- (Ri) node[pos=0.4,above right=-4.5] {$\vb{r}_{i,\text{cm}}$};
  
  % AXES
  \fill[red!80!black] (R) circle(0.02);
  \draw (M)++(\anga:0.05) --++ (\anga:\A); % axis above
  \draw (R) --++ (\anga:1.2*\A); % axis above
  \pic[rotate=\anga-90] at (\anga:0.9*\A) {rotarr}; % rotation arrow
  \node[mydarkgreen,right=2] at (W3) {$\omega$};
  \draw[<->] (\anga:0.65*\A) --++ (\ang:\d) % distance/radius R
    node[pos=0.5] {\contour{white}{$d$}};
  
\end{tikzpicture}


\end{document}