Rutherford scattering

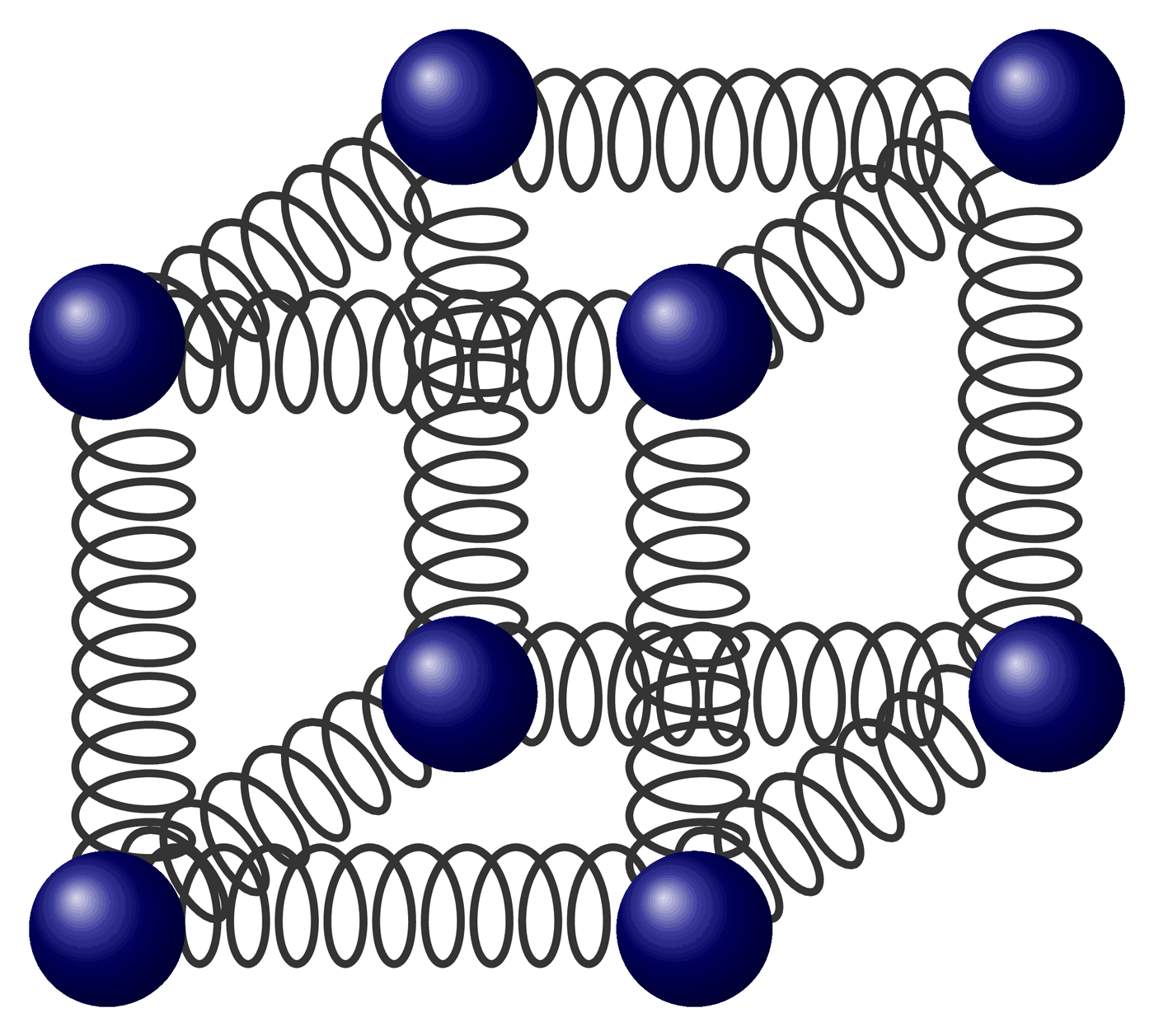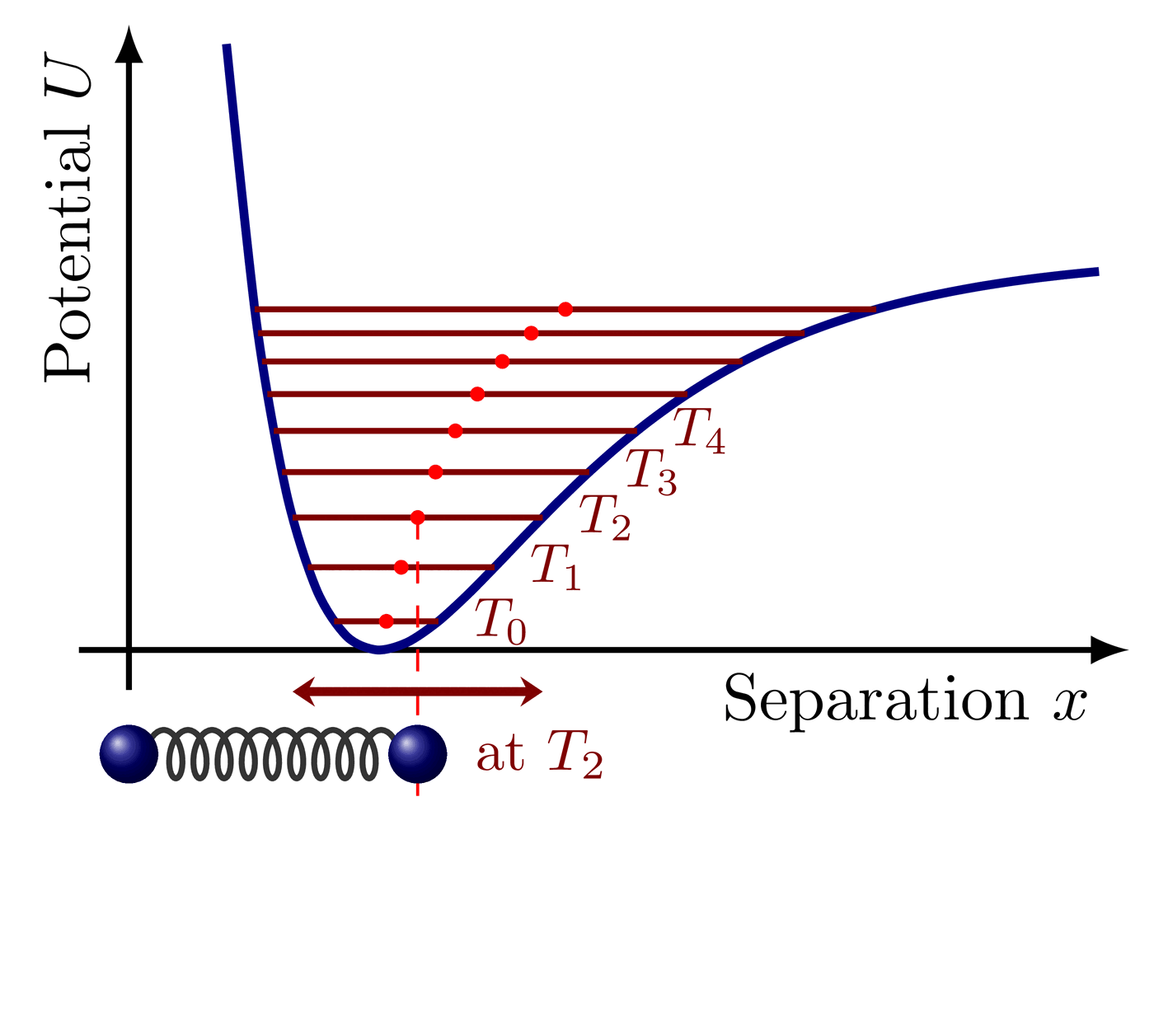
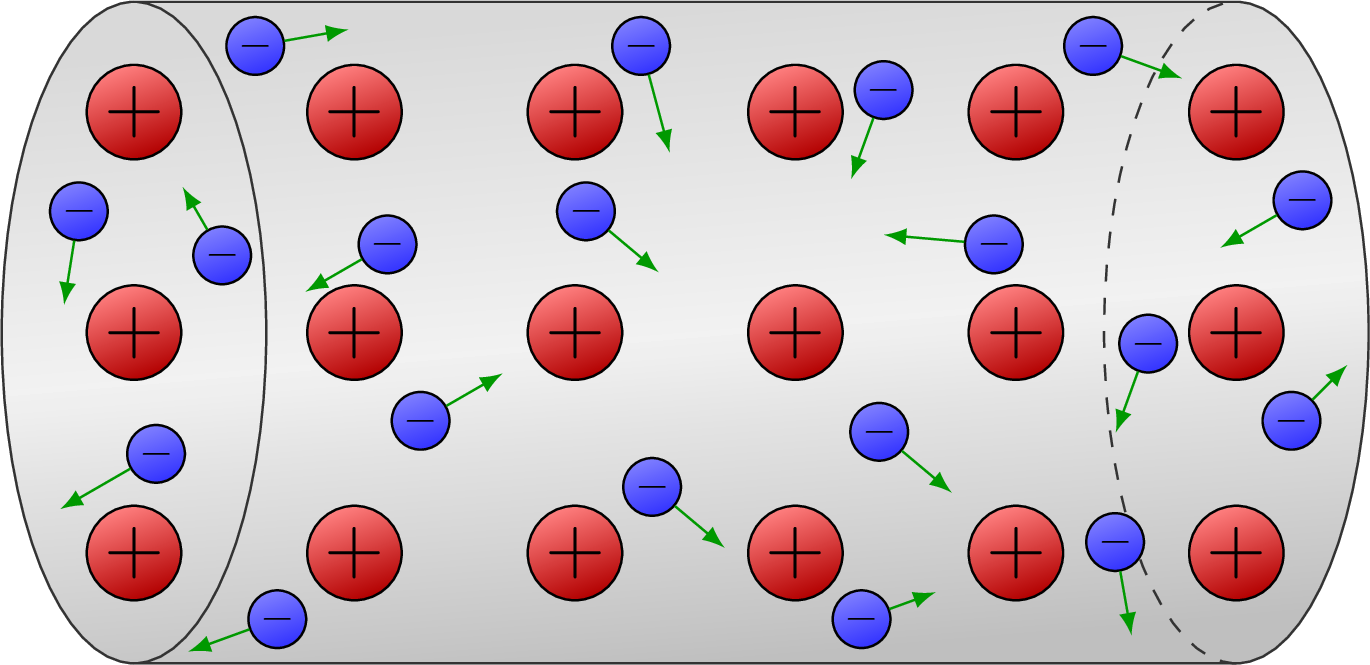
The geometry of Rutherford scattering of α particles off gold nuclei is a hyperbolic trajectory as a function of the impact parameter. See Wikipedia or Hyperphysics. These figures were used in a presentation on Rutherford’s discovery of the nucleus.

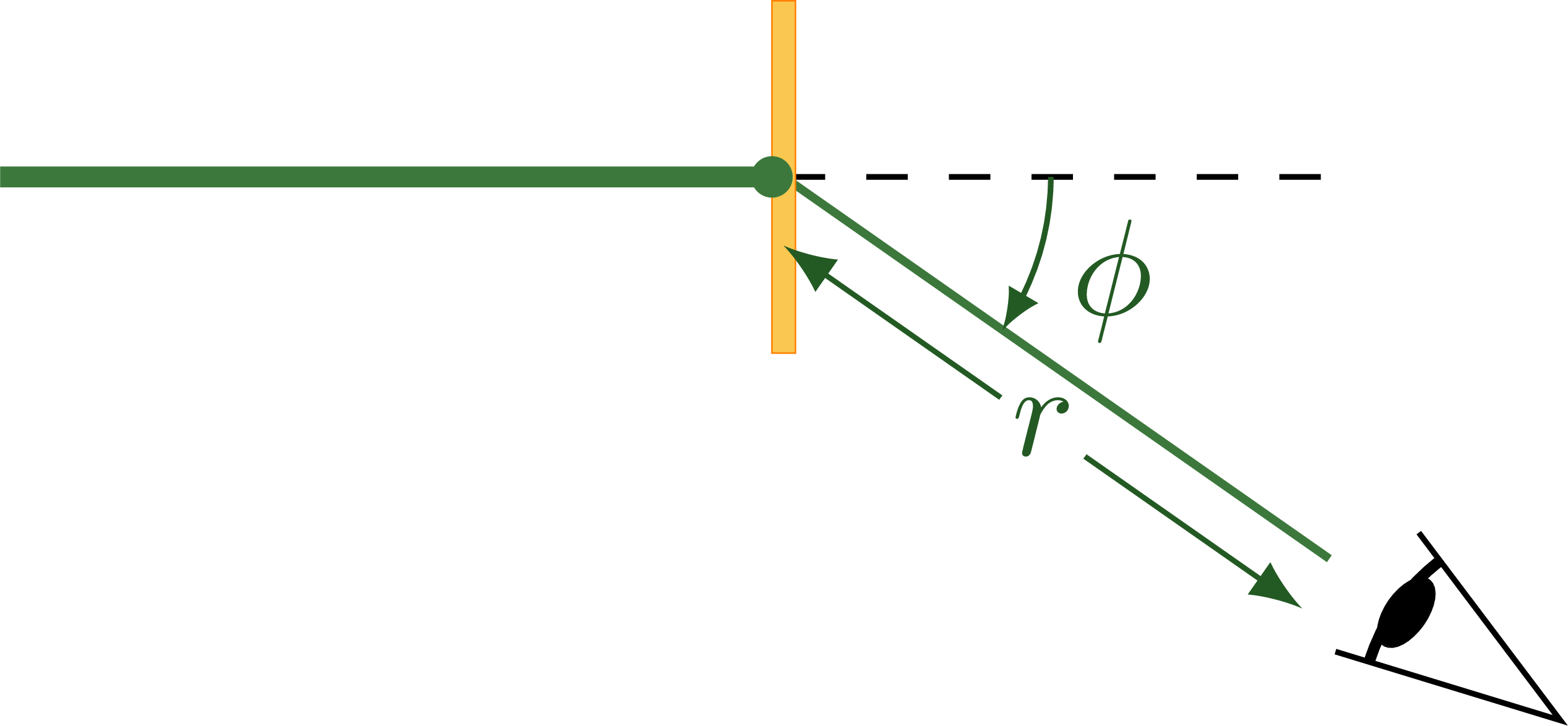
Setup of the gold foil experiment:

Hyperbolic trajectory of an α particle in Rutherford scattering, following Rutherford’s historic 1911 paper:

Extreme backscattering:

Triangle NOA to compute the angle of deviation φ = π – 2θ

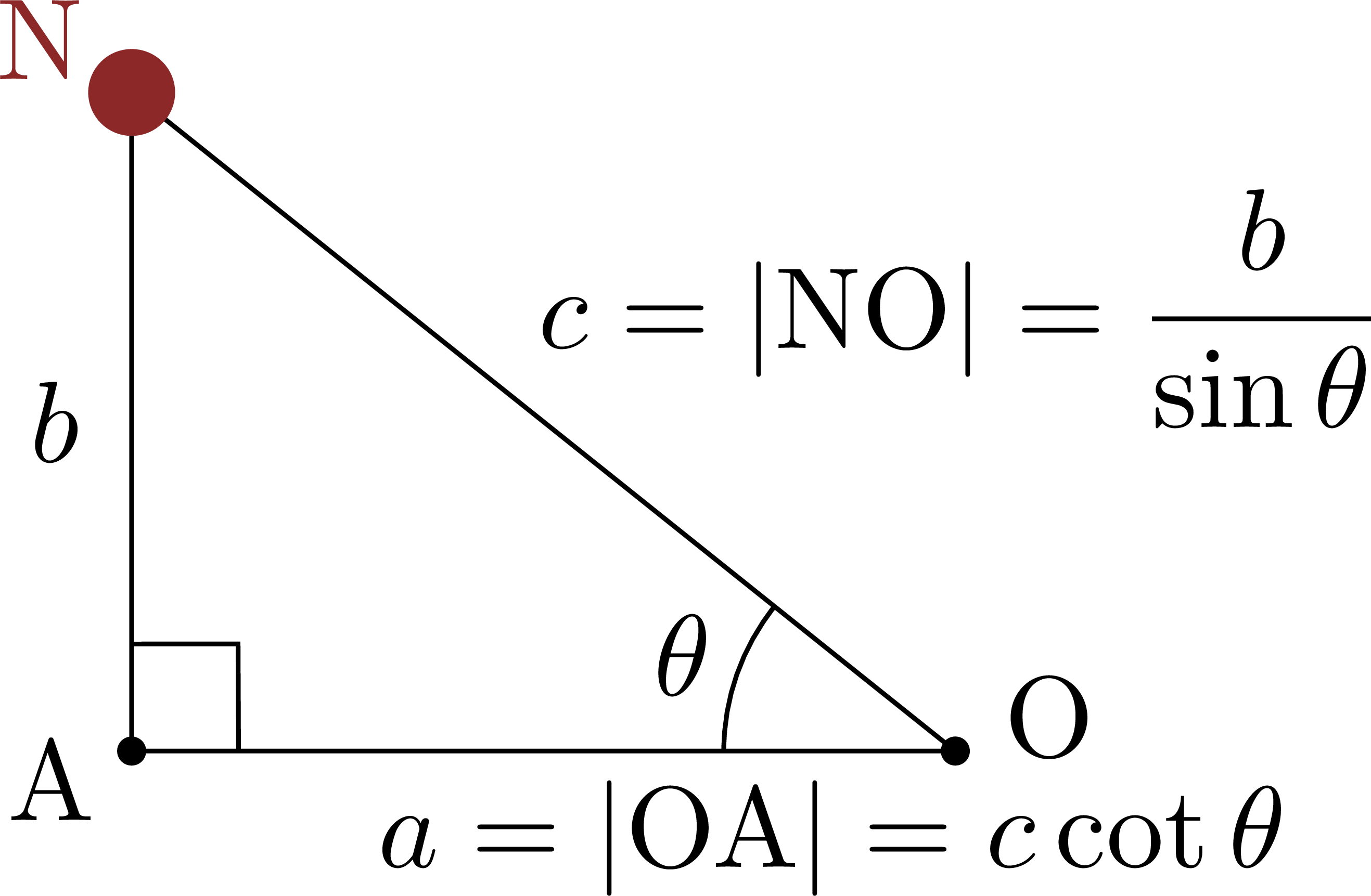
Several hyperbolic trajectories in Rutherford scattering:

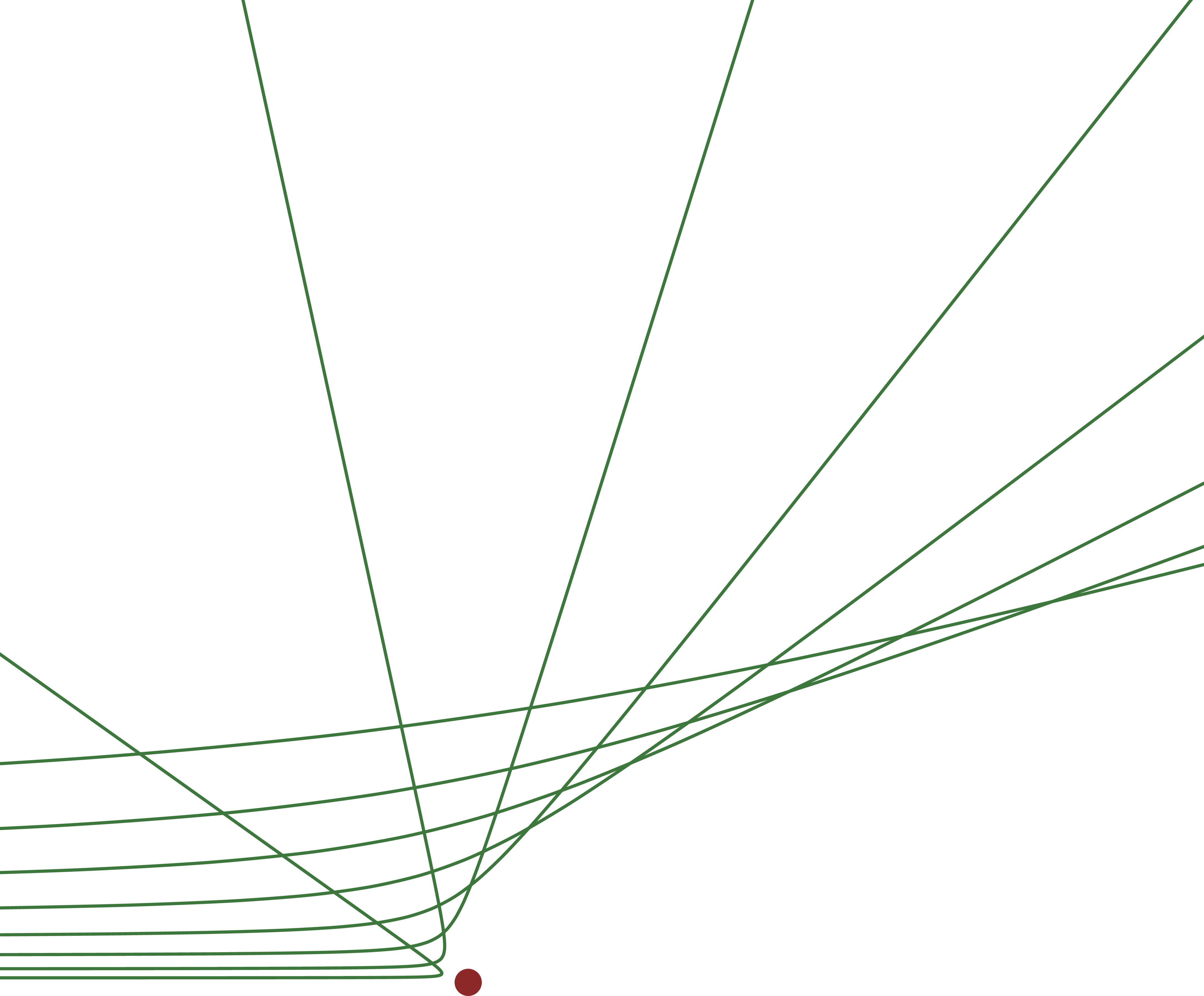
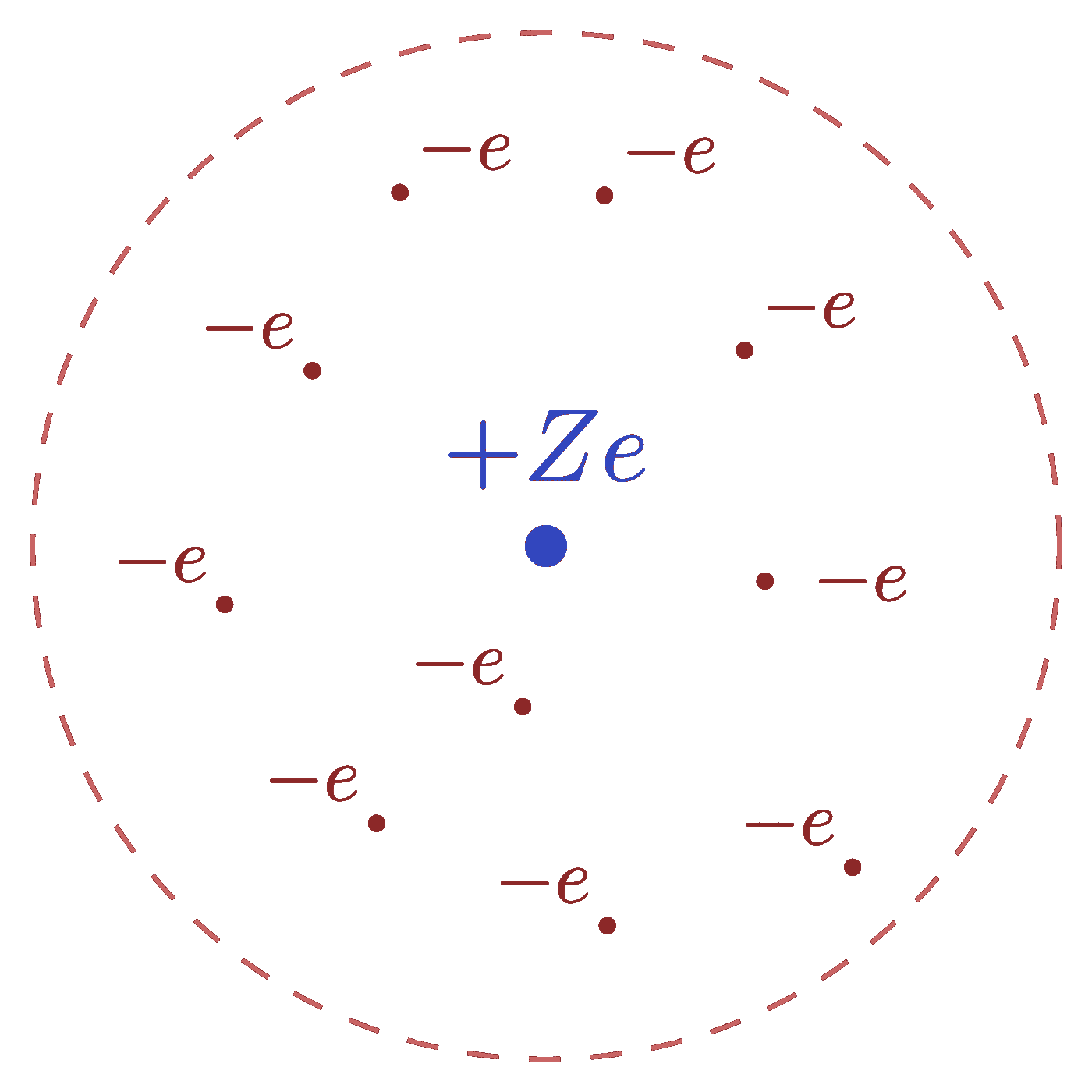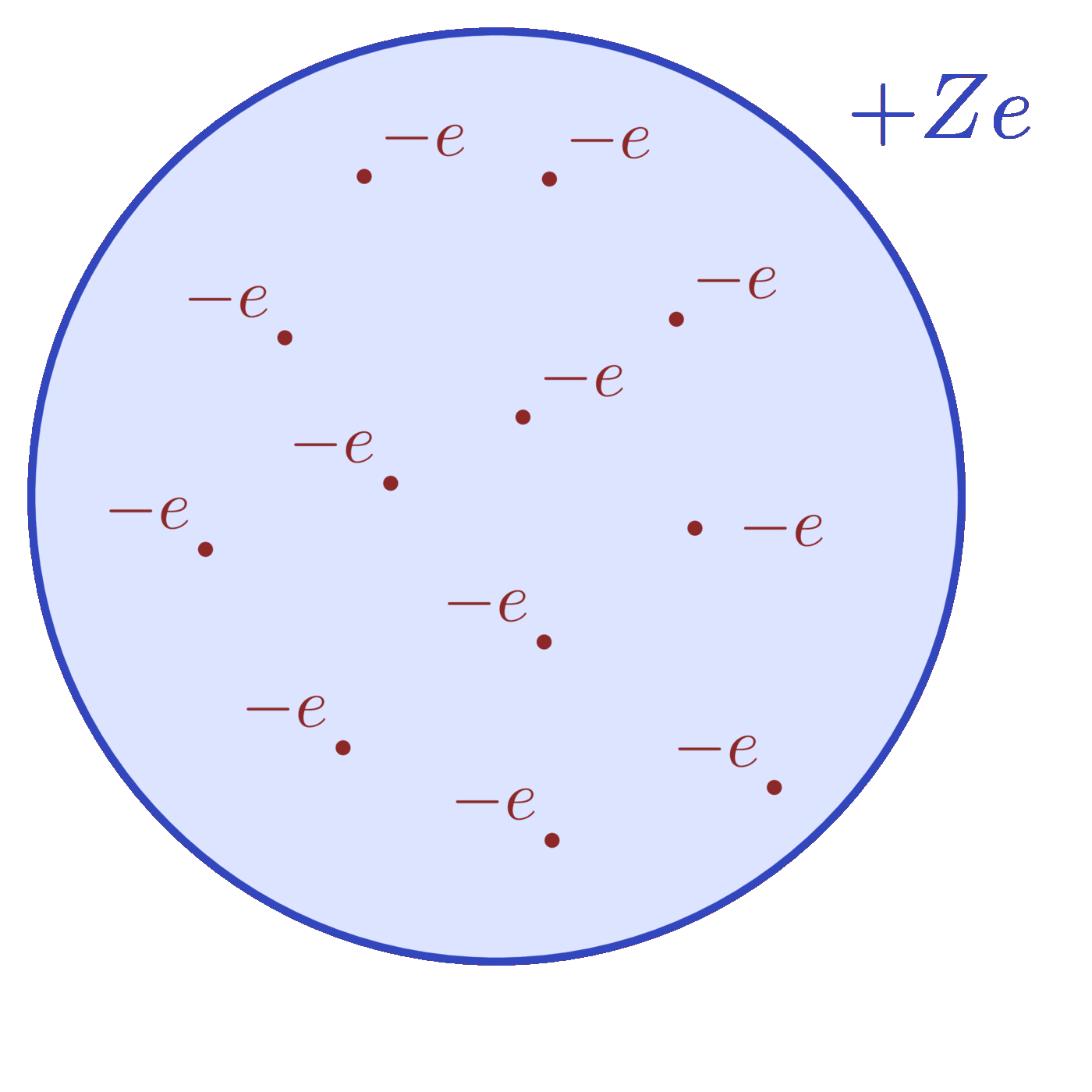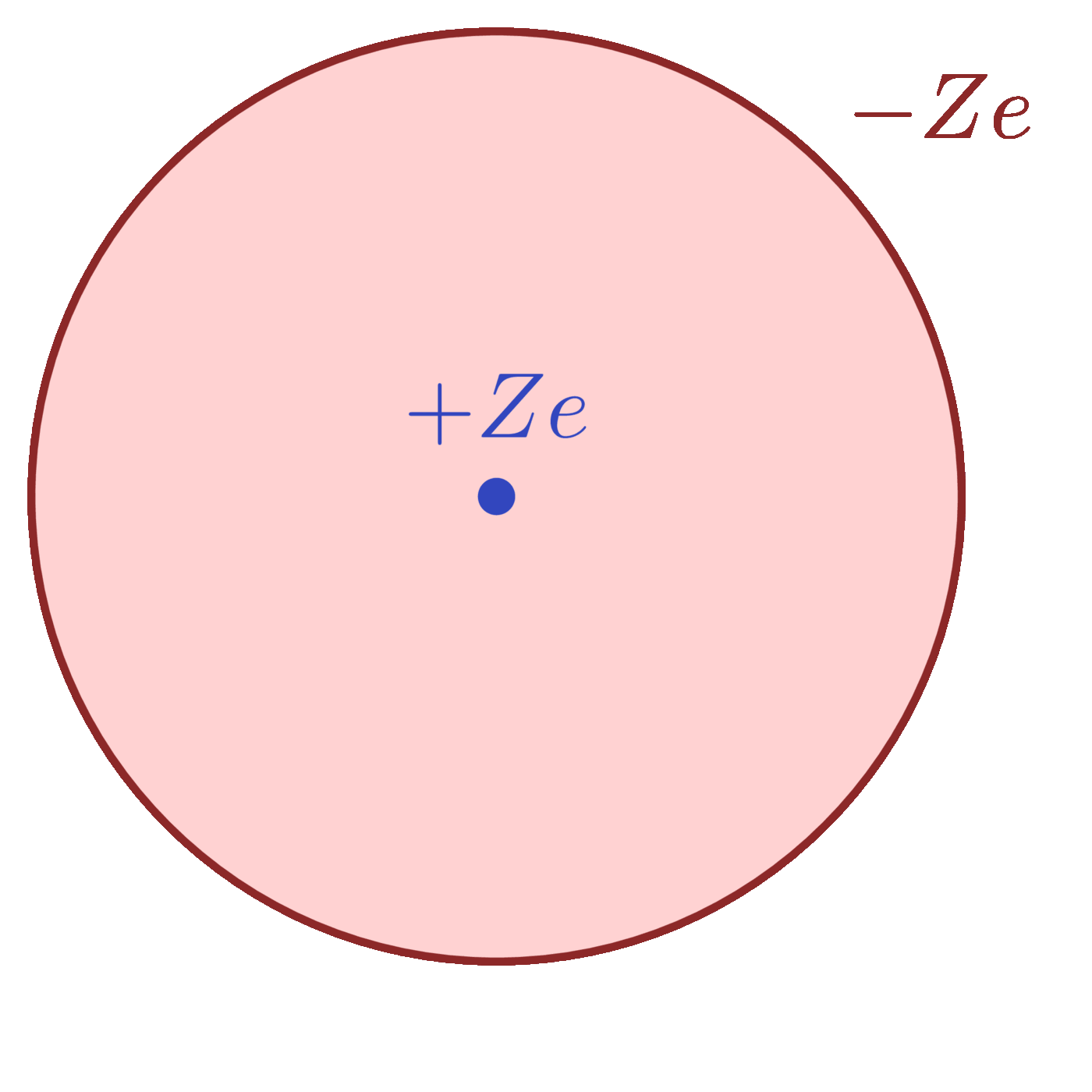
Compound vs. single scattering:

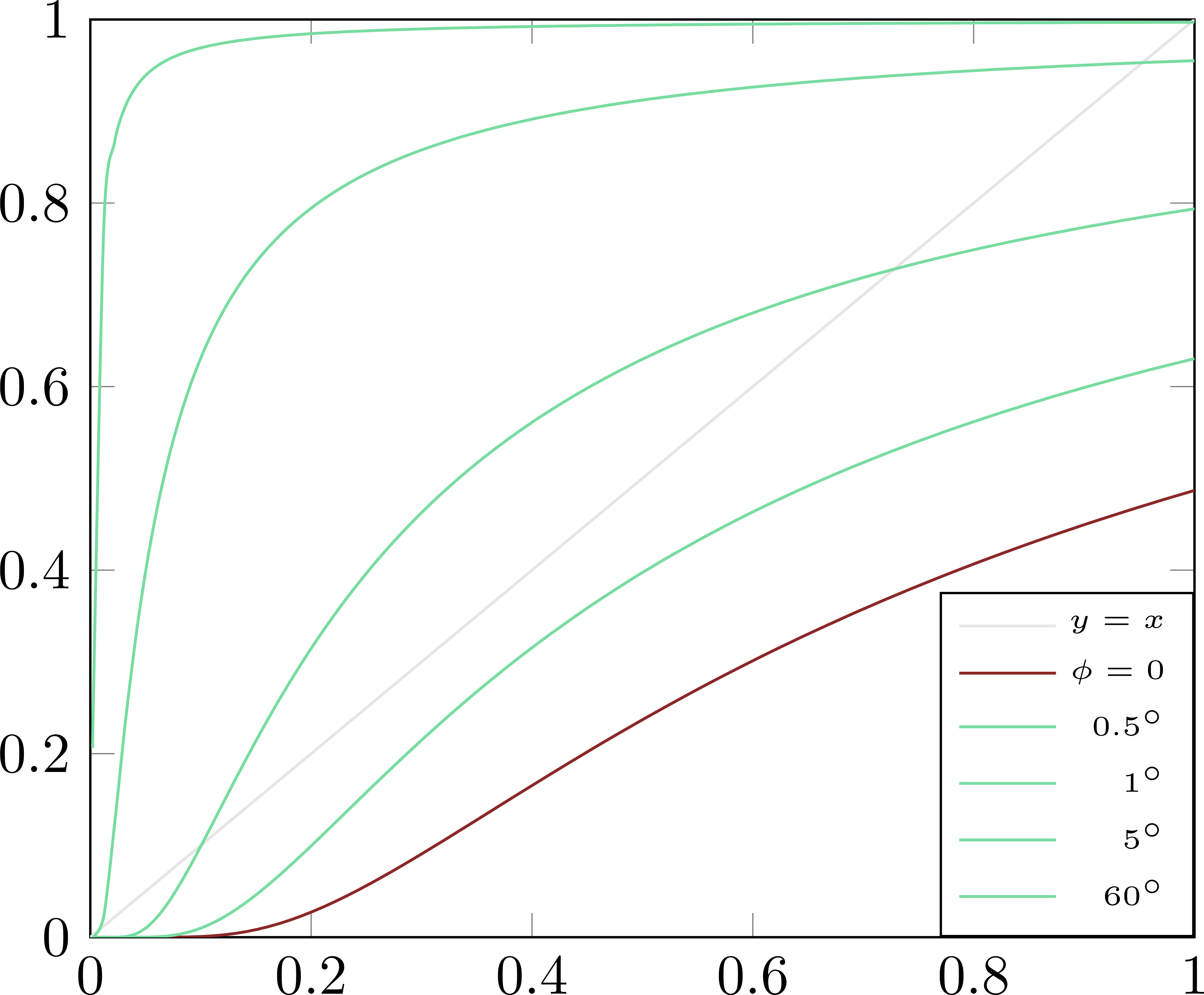
Edit and compile if you like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
% Author: Izaak Neutelings (July 2017)
% Sources:
%   https://www.tandfonline.com/doi/abs/10.1080/14786440508637080
%   https://indico.cern.ch/event/1126814/contributions/4729554/attachments/2386887/4079372/Izaak_paper_reading_Rutherford_nucleus_20170713_v5.pdf
\documentclass[border=3pt,tikz]{standalone}
\usepackage{amsmath} % for \dfrac
\usepackage{tikz}
\tikzset{>=latex} % for LaTeX arrow head
\usepackage{pgfplots} % for the axis environment
\usetikzlibrary{calc} % to do arithmetic with coordinates
\usetikzlibrary{angles,quotes} % for pic
\usetikzlibrary{arrows.meta} % for arrow size
\usetikzlibrary{bending} % for arrow head angle
\tikzstyle{bend>}=[-{Latex[flex'=1,length=3,width=2.5]}]
\tikzstyle{bend<}=[{Latex[flex'=1,length=3,width=2.5]}-]
% colors
%\definecolor{mylightblue}{RGB}{170,170,230}
\definecolor{mylightgrey}{RGB}{230,230,230}
\definecolor{mygrey}{RGB}{190,190,190}
\definecolor{mydarkgrey}{RGB}{110,110,110}
\definecolor{mygreen}{RGB}{120,220,160}
\definecolor{mydarkgreen}{RGB}{60,120,60}
\definecolor{myverydarkgreen}{RGB}{35,90,35}
\definecolor{mydarkred}{RGB}{140,40,40}
\definecolor{mylightblue}{RGB}{220,228,255}
\definecolor{myblue}{RGB}{183,191,229}
\definecolor{mydarkblue}{RGB}{50,70,190}
\definecolor{mygold}{RGB}{250,200,80}
% mark right angle
\newcommand{\MarkRightAngle}[4][1.3mm]{
  \coordinate (tempa) at ($(#3)!#1!(#2)$);
  \coordinate (tempb) at ($(#3)!#1!(#4)$);
  \coordinate (tempc) at ($(tempa)!0.5!(tempb)$);%midpoint
  \draw (tempa) -- ($(#3)!2!(tempc)$) -- (tempb);
}
\begin{document}
 
 
הההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההה
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX

Click to download: hyperbola.tex • hyperbola.pdf
Open in Overleaf: hyperbola.tex