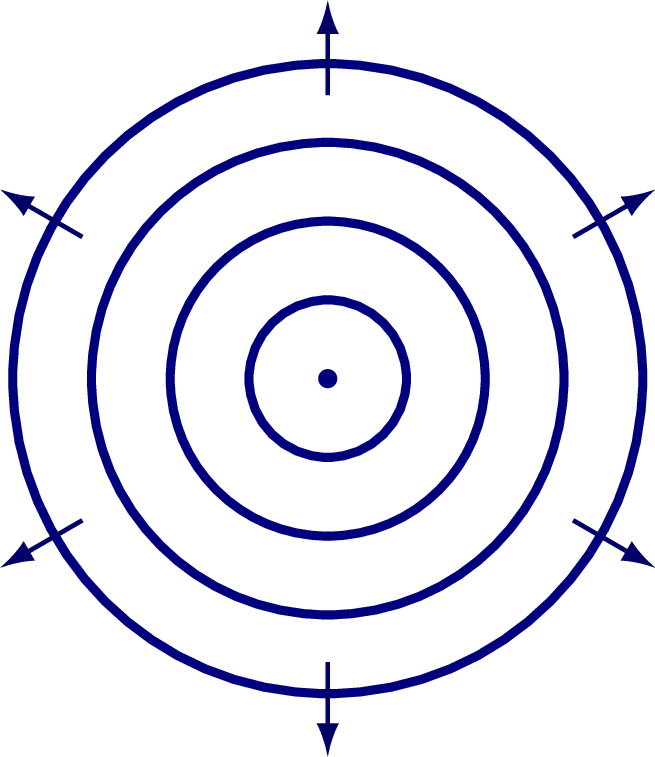
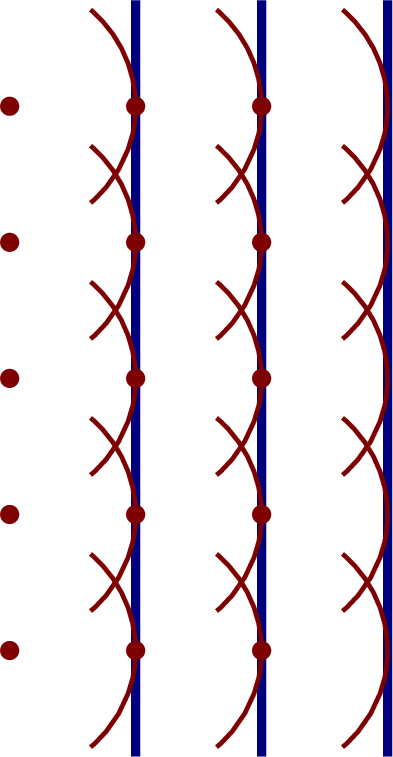
The Huygens–Fresnel principle considers each point in a wavefront as a new point sources emitting wavelets that add up to new wave fronts. This can be use to explain spherical or plane waves, and even diffraction and refraction.
For more related figures, please see the Optics category.
Edit and compile if you like:
% Author: Izaak Neutelings (May 2020)
% Inspiration: https://tex.stackexchange.com/questions/285578/how-to-draw-parallelepiped-and-cube-with-latex/288101#288101
\documentclass[border=3pt,tikz]{standalone}
\usetikzlibrary{arrows,arrows.meta}
\tikzset{>=latex} % for LaTeX arrow head
\tikzstyle{myarr}=[-{Latex[length=3,width=2]}]
\colorlet{myblue}{blue!50!black}
\colorlet{myred}{black!50!red}
% WAVEFRONT
\def\p{0.03}
\def\r{0.25}
\tikzset{
wavefront/.pic={
\tikzset{/wavefront/.cd,#1}
\fill (0,0) circle (\p);
\draw (\wang:\r) arc(\wang:-\wang:\r);
}
/wavefront/.search also={/tikz},
/wavefront/.cd,
ang/.store in=\wang, ang={60},
}
\begin{document}
% Point source
\begin{tikzpicture}
\fill[myblue] (0,0) circle (\p);
\foreach \i in {1,...,4}{
\draw[myblue,thick] (0,0) circle (\r*\i);
}
\foreach \a in {30,90,...,330}{
\draw[myarr,myblue!80!black] (\a:\r*3.6) --++ (\a:1.2*\r);
}
\end{tikzpicture}
% Hughens principle
\begin{tikzpicture}
\def\r{0.4}
\fill[myblue] (0,0) circle (\p);
\foreach \i in {1,...,3}{
\draw[myblue,thick] (70:\r*\i) arc(70:-70:\r*\i);
}
\foreach \a in {-45,0,45}{
\pic[myred,rotate=\a] at (\a:\r) {wavefront};
}
\foreach \a in {-45,0,45}{
\pic[myred,rotate=\a] at (\a:2*\r) {wavefront};
}
\end{tikzpicture}
% Hughens principle plane wave
\begin{tikzpicture}
\def\N{5}
\def\r{0.4}
\def\h{1.2}
\foreach \i in {1,...,3}{
\draw[myblue,thick] (\r*\i,-\h) -- (\r*\i,\h);
\foreach \j [evaluate={\y=(\j-(\N+1)/2)*(1.8*\h)/\N;}] in {1,...,\N}{
\pic[myred] at ({\r*(\i-1)},\y) {wavefront={ang={50}}};
}
}
\end{tikzpicture}
\end{document}Click to download: optics_huygens.tex • optics_huygens.pdf
Open in Overleaf: optics_huygens.tex