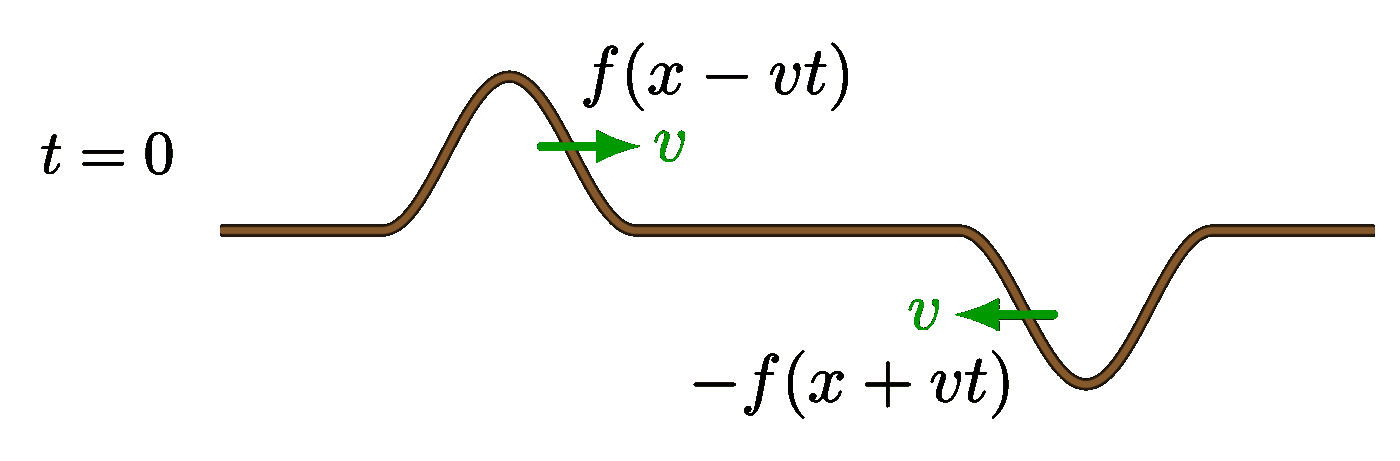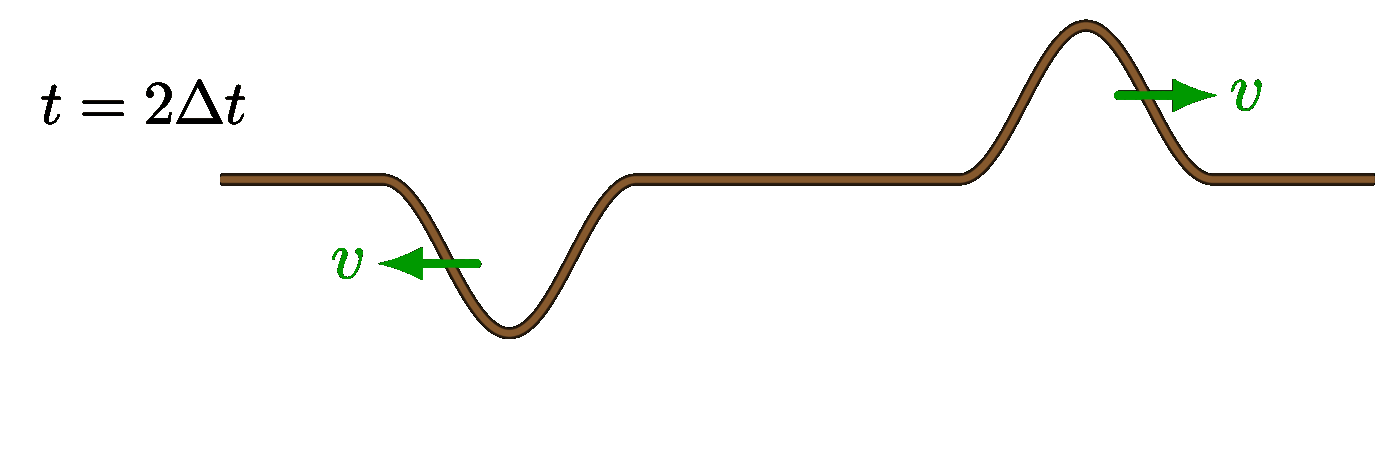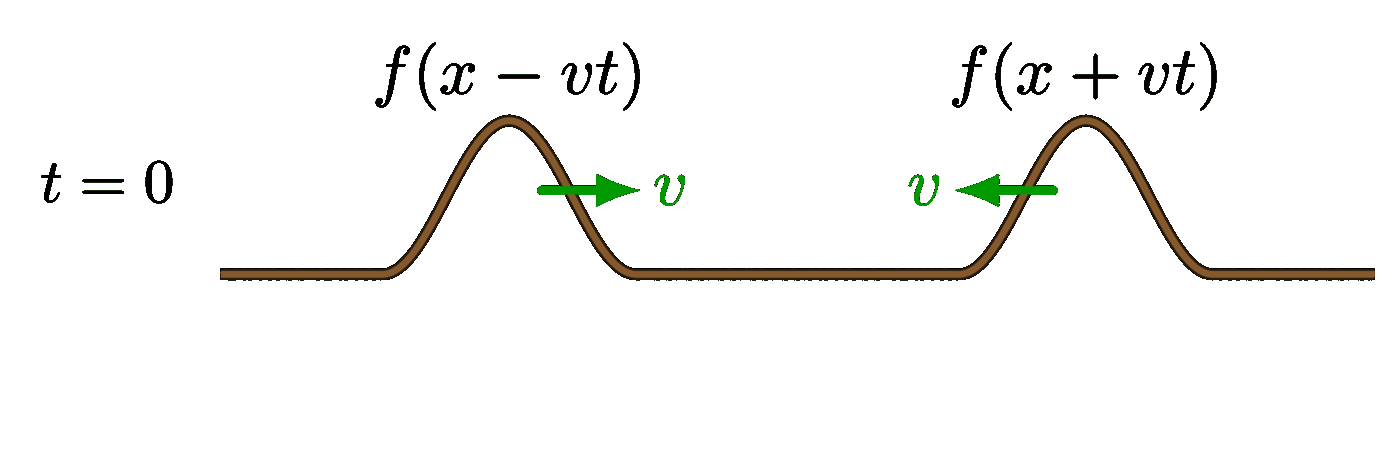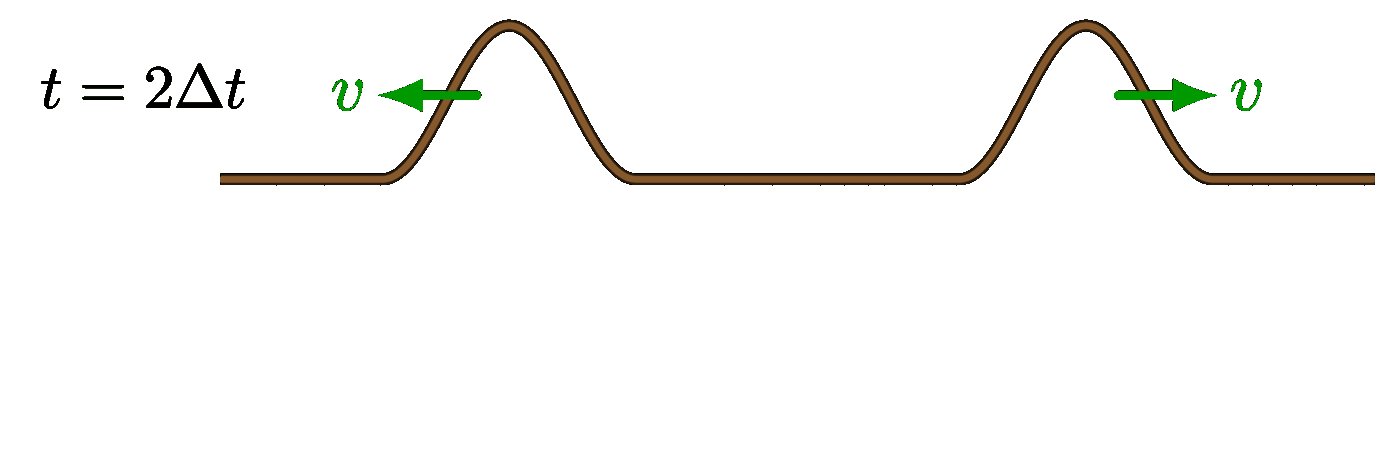
Complete destructive interference: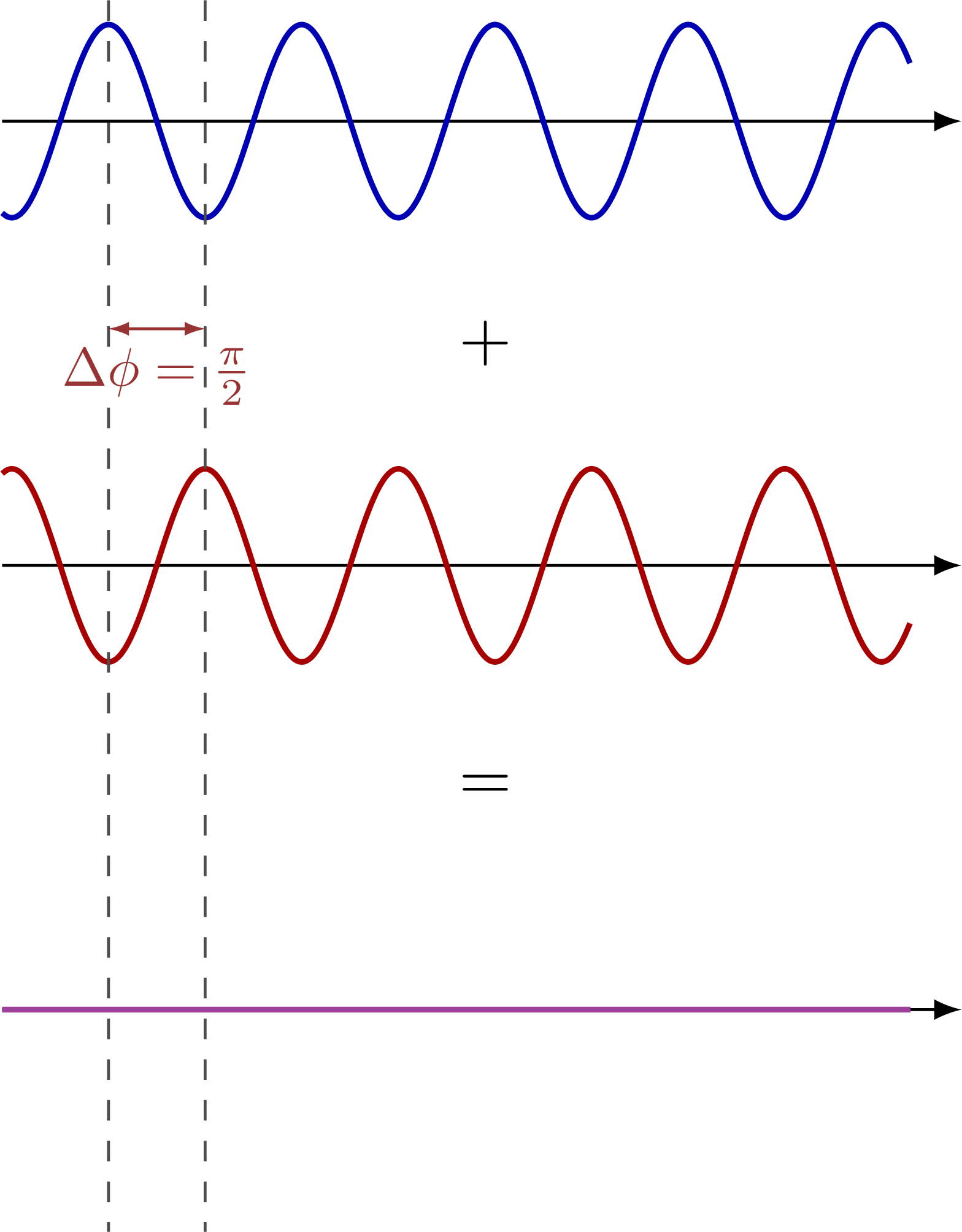 Partial destructive interference:
Partial destructive interference: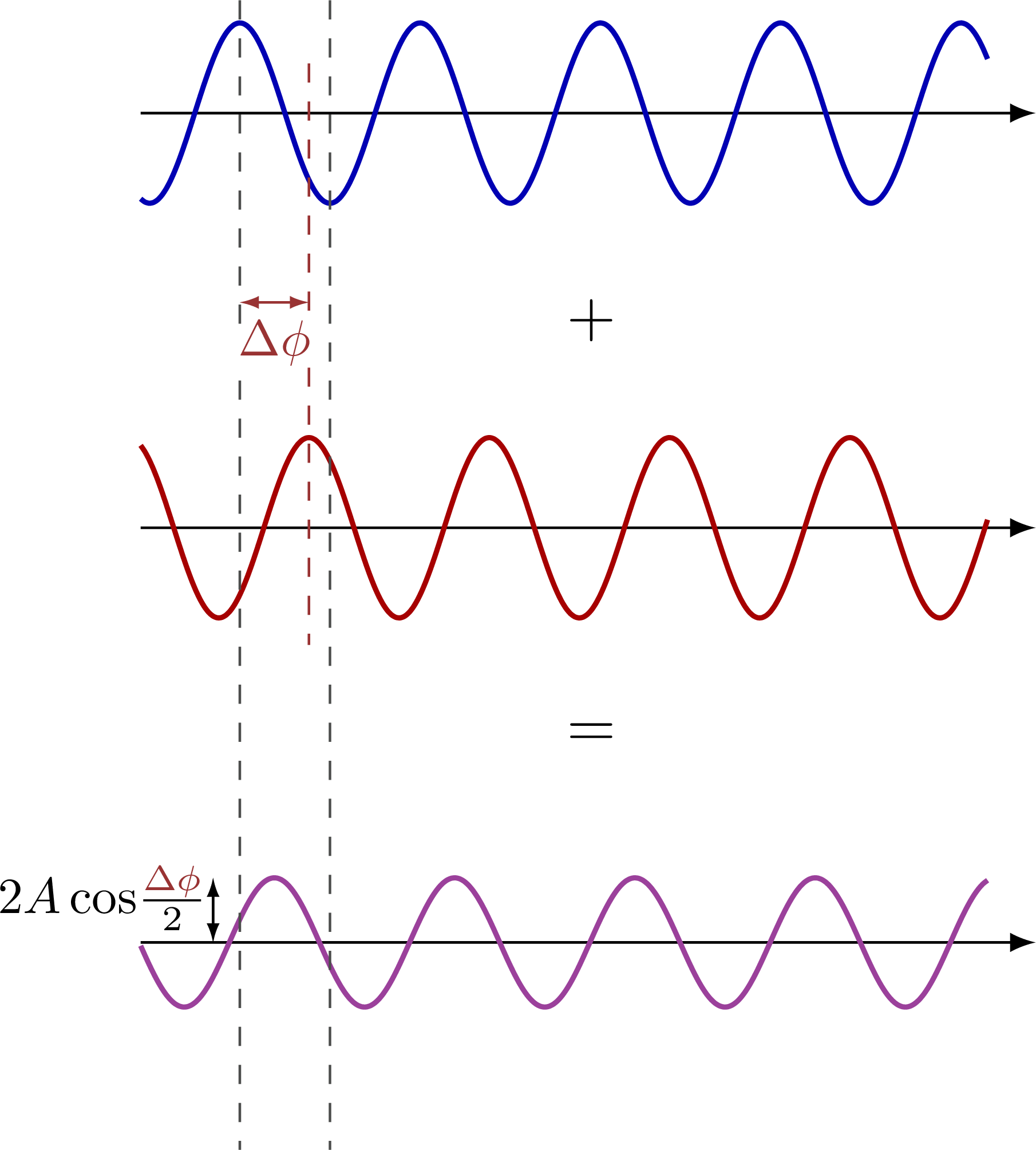 Complete constructive interference:
Complete constructive interference: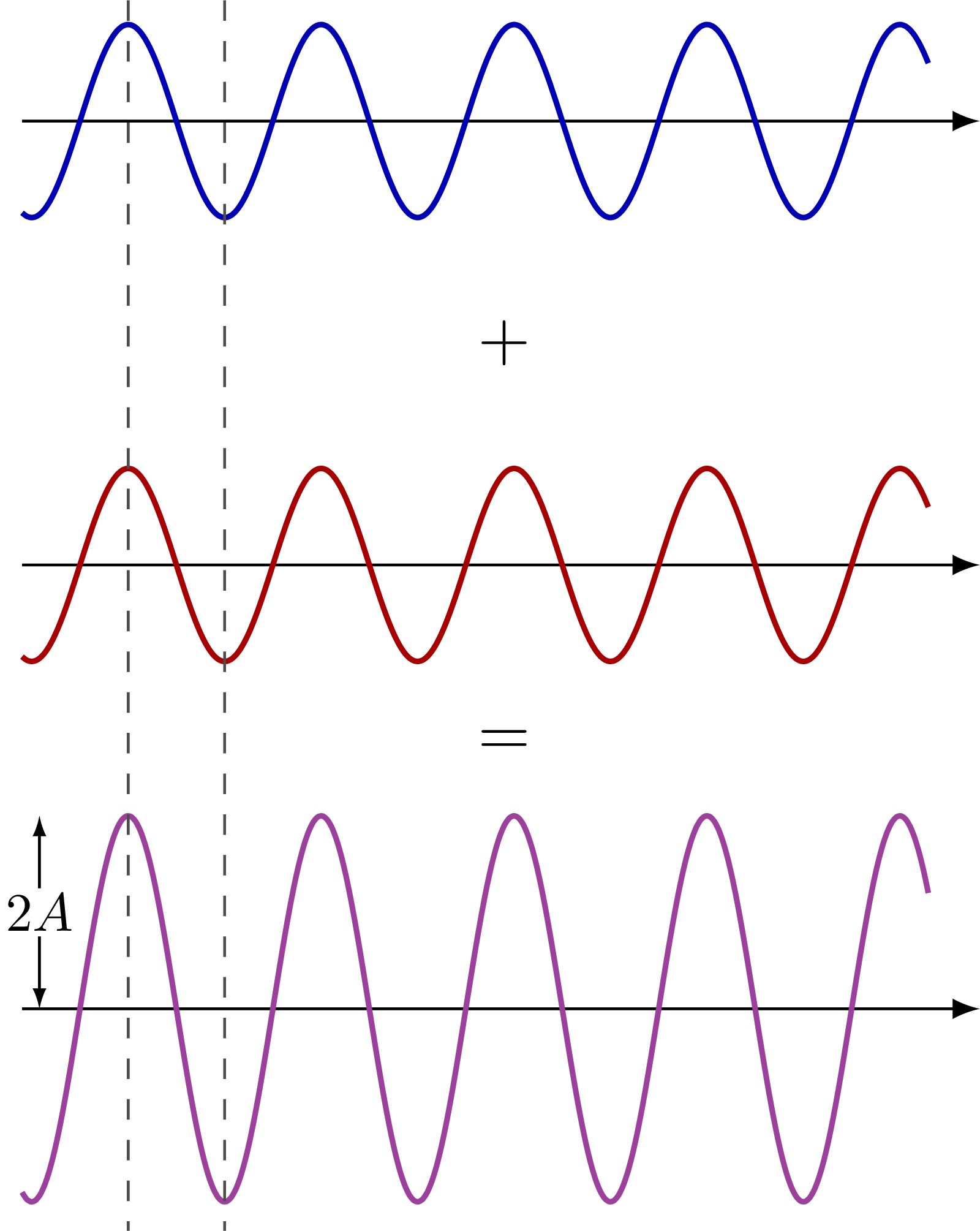 Interference pattern of two point sources in space:
Interference pattern of two point sources in space: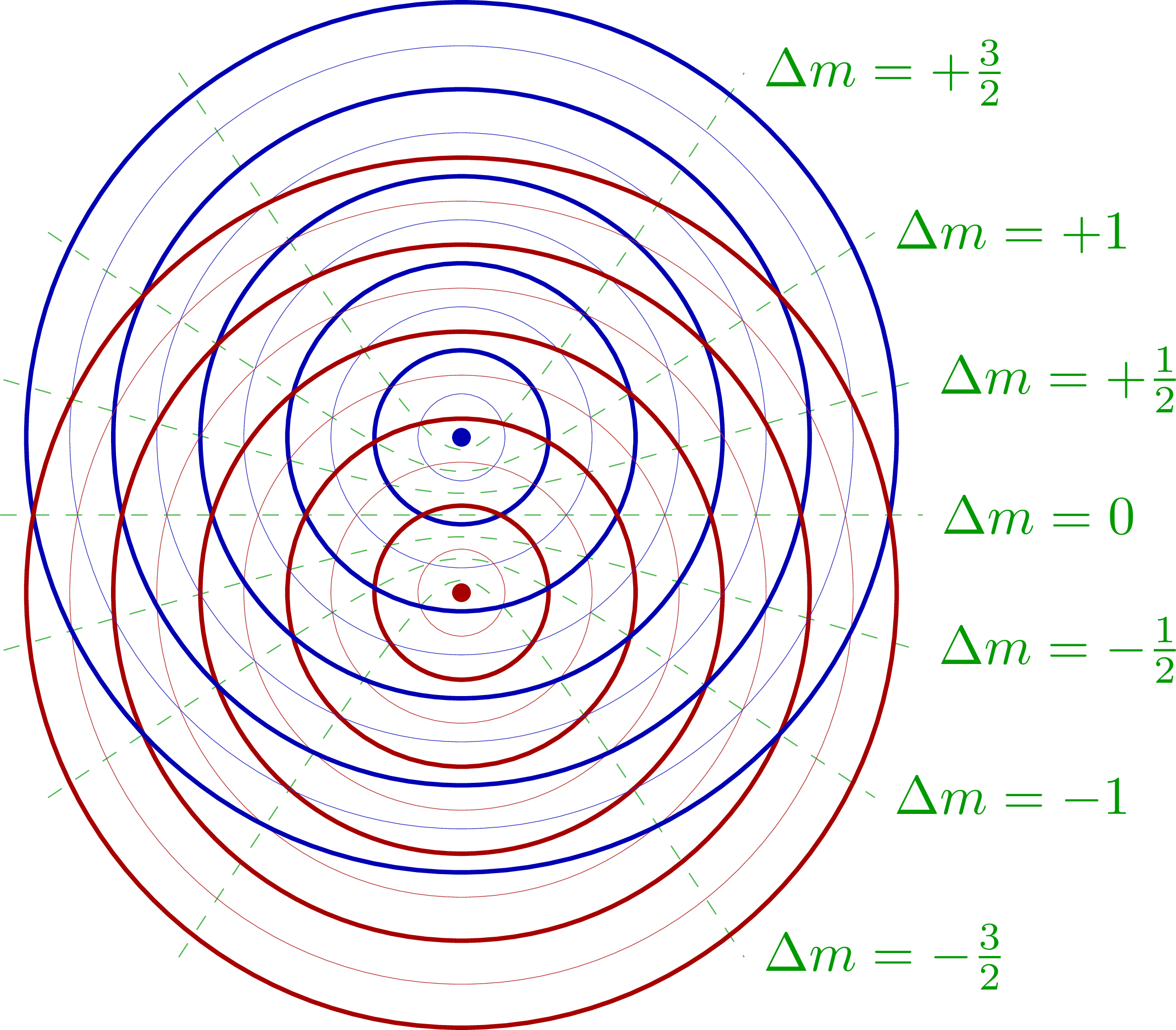 Path difference of the waves from two point sources:
Path difference of the waves from two point sources: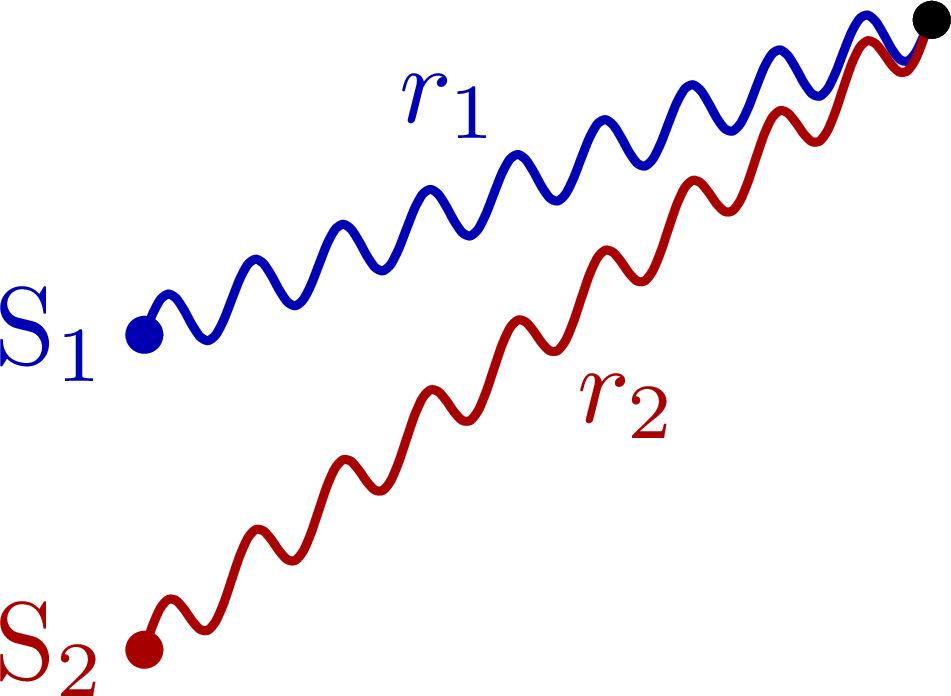
Open in Overleaf: optics_interference.tex
 Partial destructive interference:
Partial destructive interference: Complete constructive interference:
Complete constructive interference: Interference pattern of two point sources in space:
Interference pattern of two point sources in space: Path difference of the waves from two point sources:
Path difference of the waves from two point sources:
Click to download: optics_interference.tex • optics_interference.pdf% Author: Izaak Neutelings (June 2020)% Inspiration: https://tex.stackexchange.com/questions/285578/how-to-draw-parallelepiped-and-cube-with-latex/288101#288101\documentclass[border=3pt,tikz]{standalone}\usepackage[outline]{contour} % glow around text\usepackage{xcolor}\usepackage{etoolbox} %ifthen\usetikzlibrary{arrows,arrows.meta}\usetikzlibrary{calc}\usetikzlibrary{decorations.markings}\usetikzlibrary{angles,quotes} % for pic (angle labels)\tikzset{>=latex} % for LaTeX arrow head\contourlength{1.6pt}\colorlet{myblue}{blue!70!black}\colorlet{myred}{red!65!black}\colorlet{mypurple}{red!50!blue!95!black!75}\colorlet{mylightgreen}{green!60!black!70}\colorlet{mygreen}{green!60!black}\colorlet{myredgrey}{red!50!black!80}\tikzstyle{wave}=[myblue,thick]\tikzstyle{mydashed}=[black!70,dashed,thin]\tikzstyle{mymeas}=[{Latex[length=3,width=2]}-{Latex[length=3,width=2]},thin]\begin{document}% DESTRUCTIVE INTERFERENCE\def\A{0.5}\def\k{360}\def\xmin{-0.3}\def\xmax{4.4}\def\h{2.3}\def\lang{90}\def\rang{270} % 720+270 = 990\def\nsamples{200}\begin{tikzpicture}%\def\angg{asin(\na/\ng*sin(\anga))}%\coordinate (O) at (0,0);
Open in Overleaf: optics_interference.tex


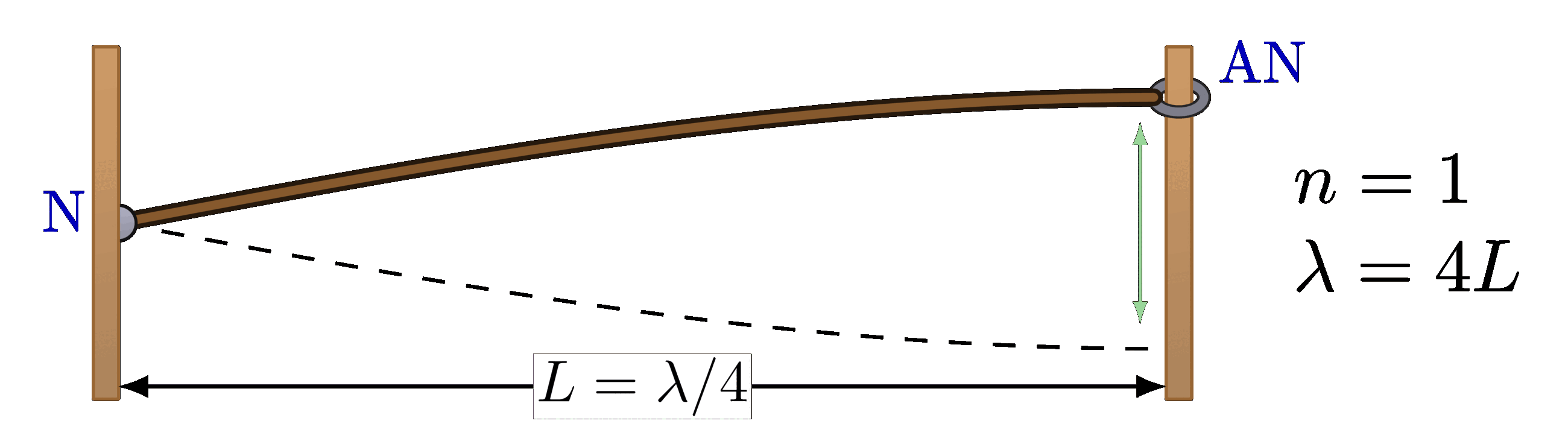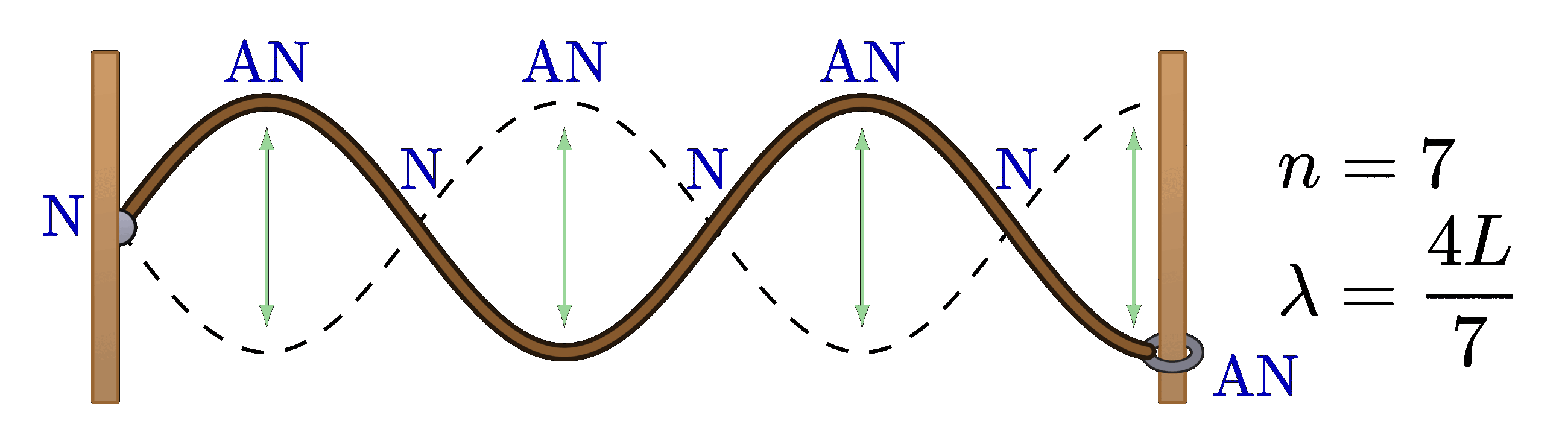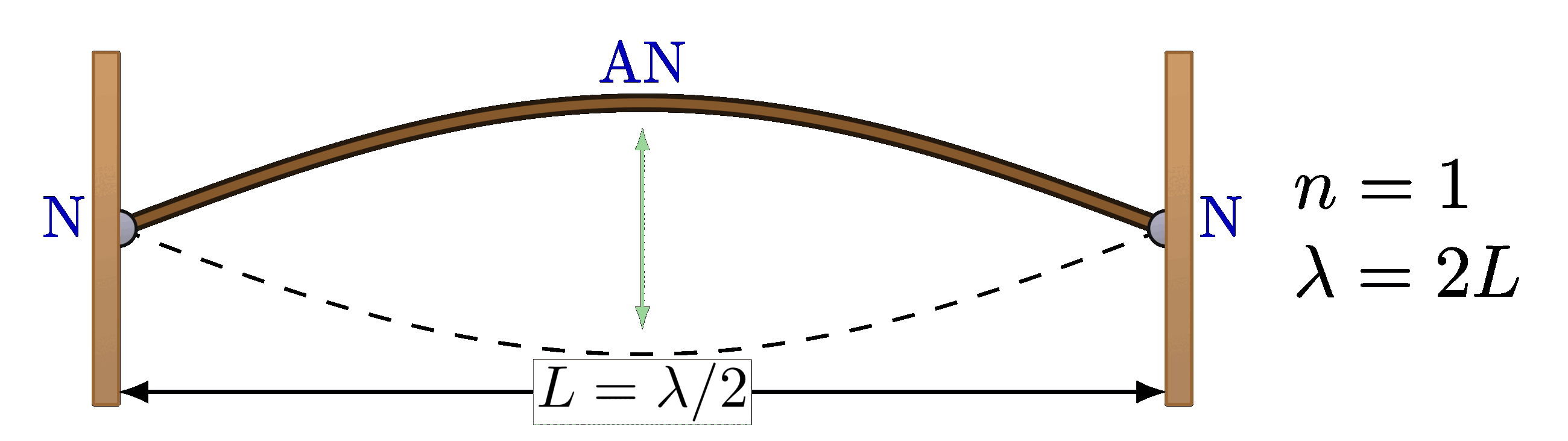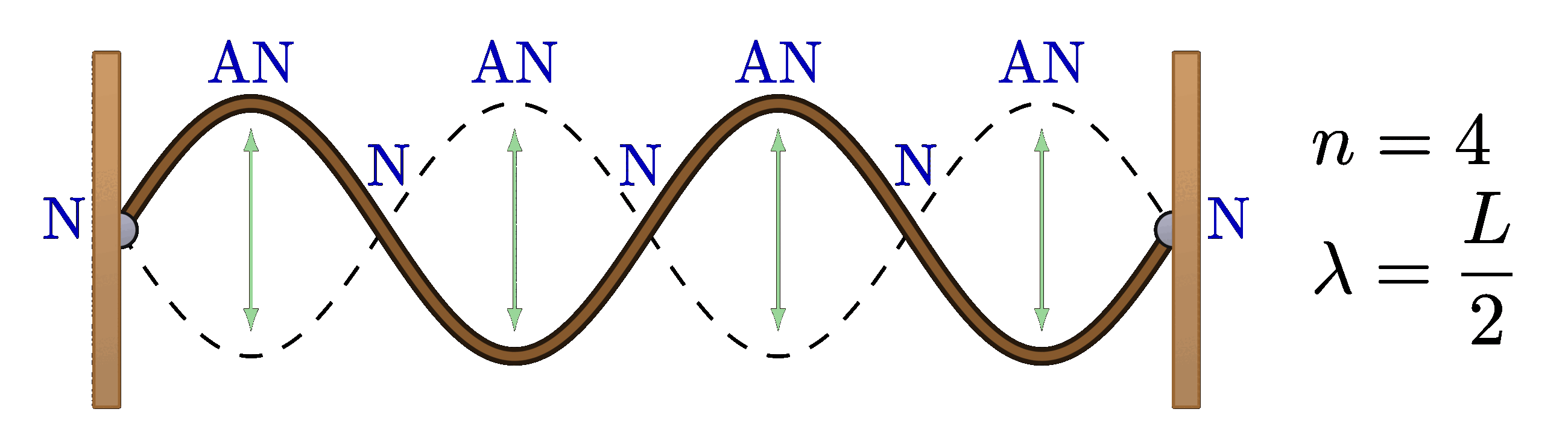


The code above seems to be incomplete. Thanks a lot for the great illustrations.
Hey Martin, Thanks for the heads up! It appears a ‘<' in the LaTeX code screwed up the HTML. It should be fixed now, but you can find the full file here: https://tikz.net/files/optics_interference.tex or open it in Overleaf via https://www.overleaf.com/docs?snip_uri=https://tikz.net/files/optics_interference.tex.
Cheers, Izaak
Thanks!