Beating waves

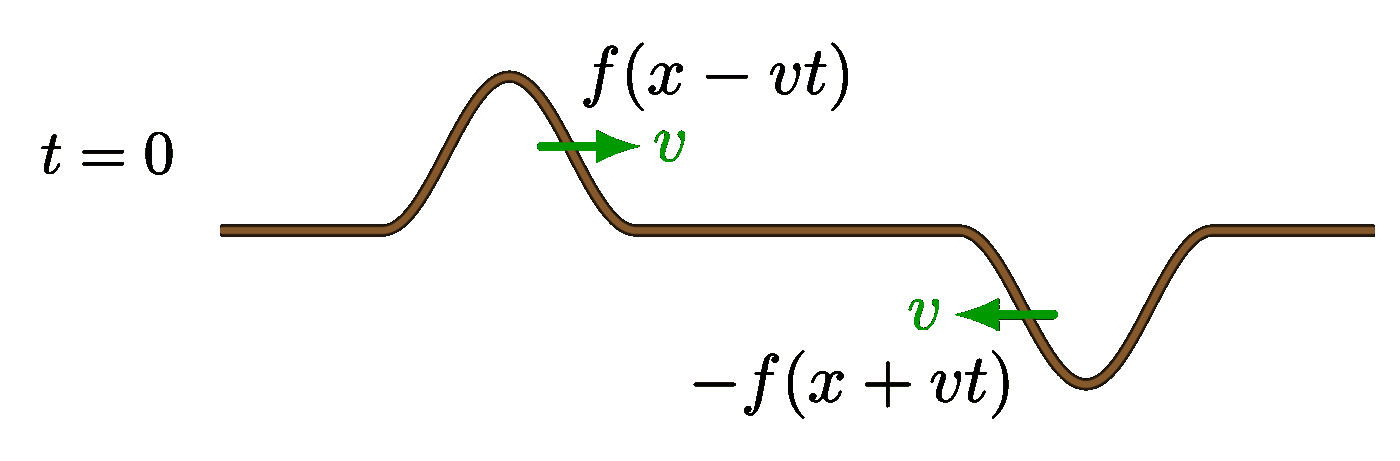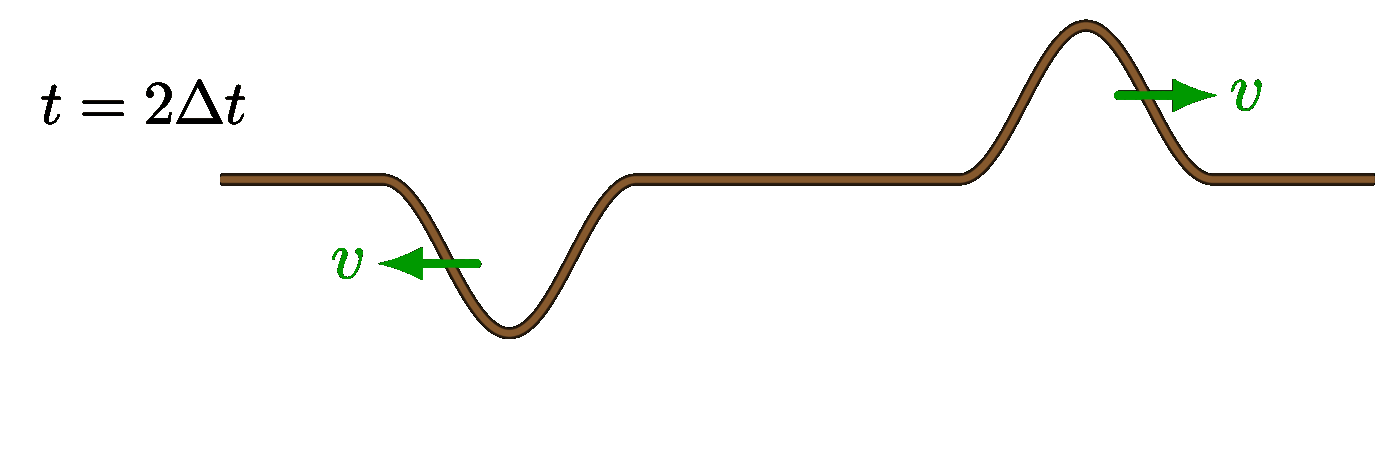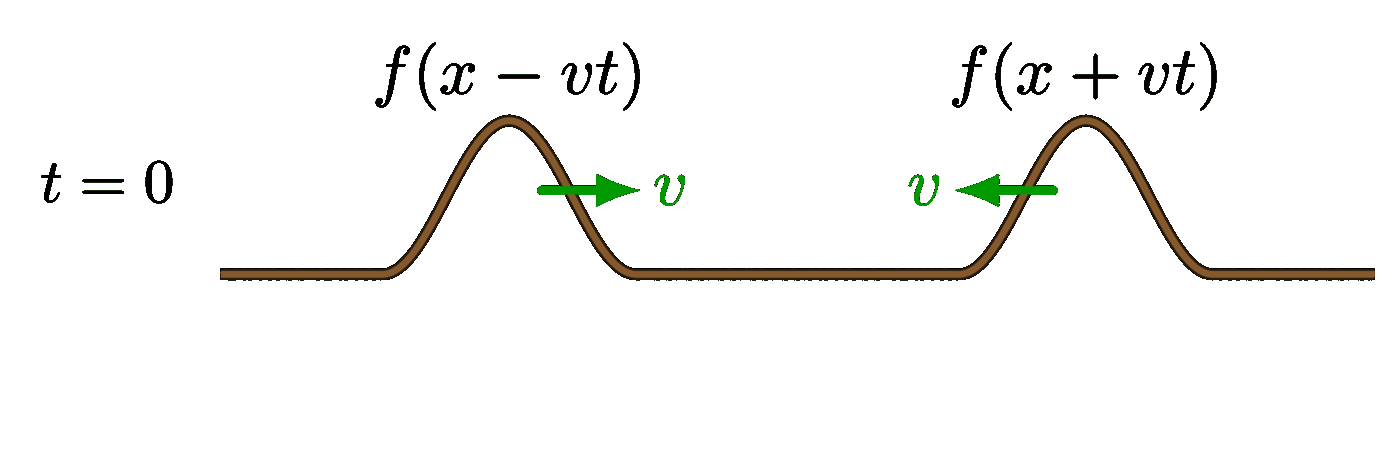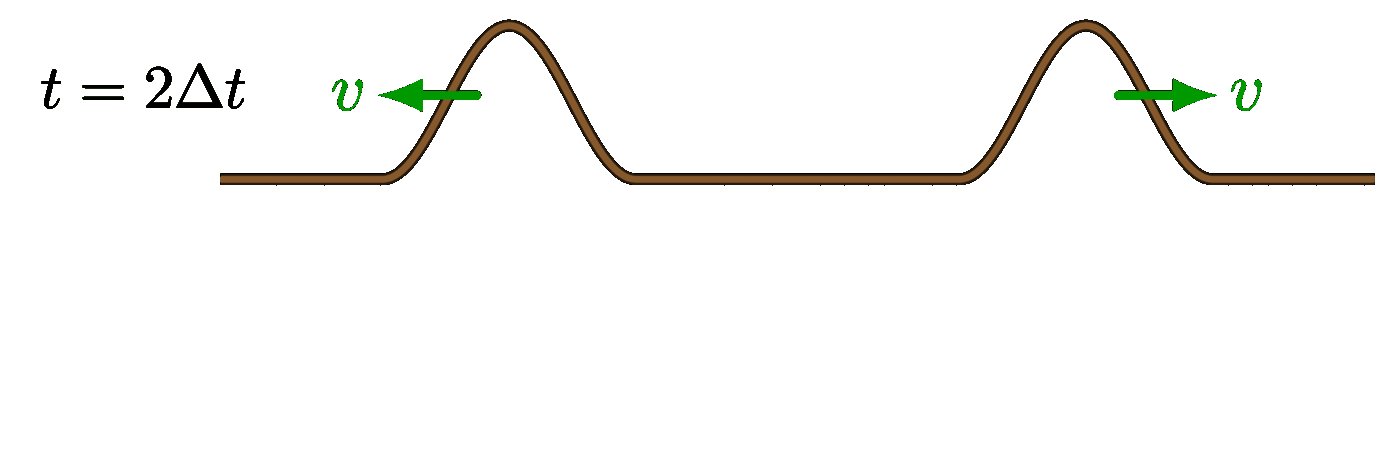
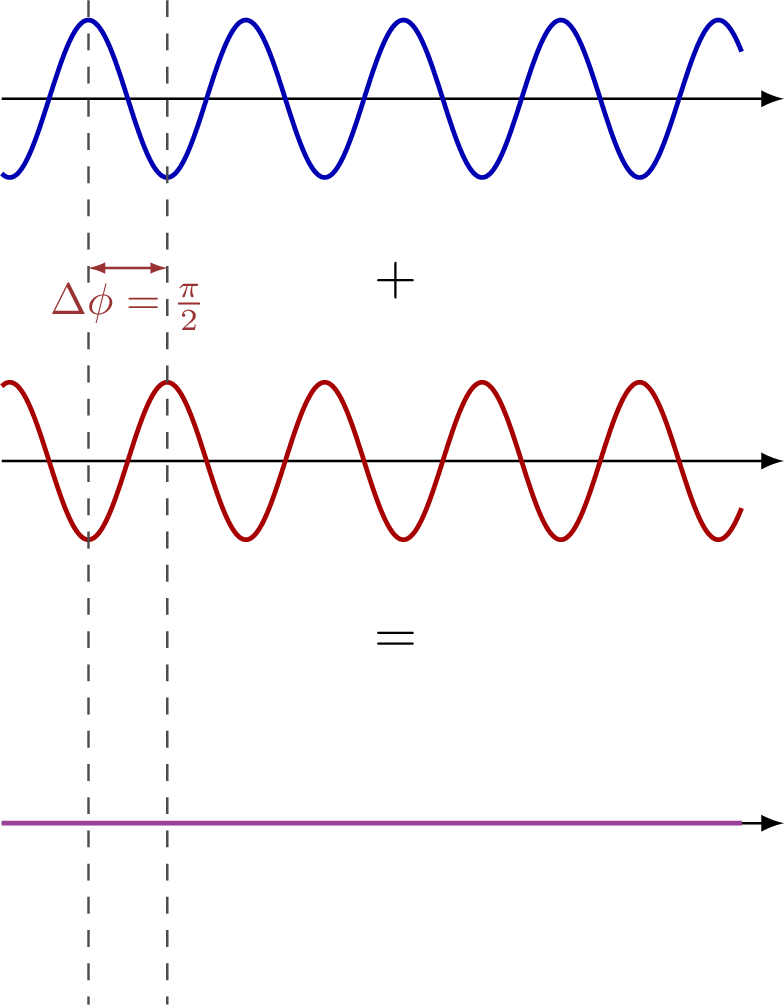
Large difference in wavelength: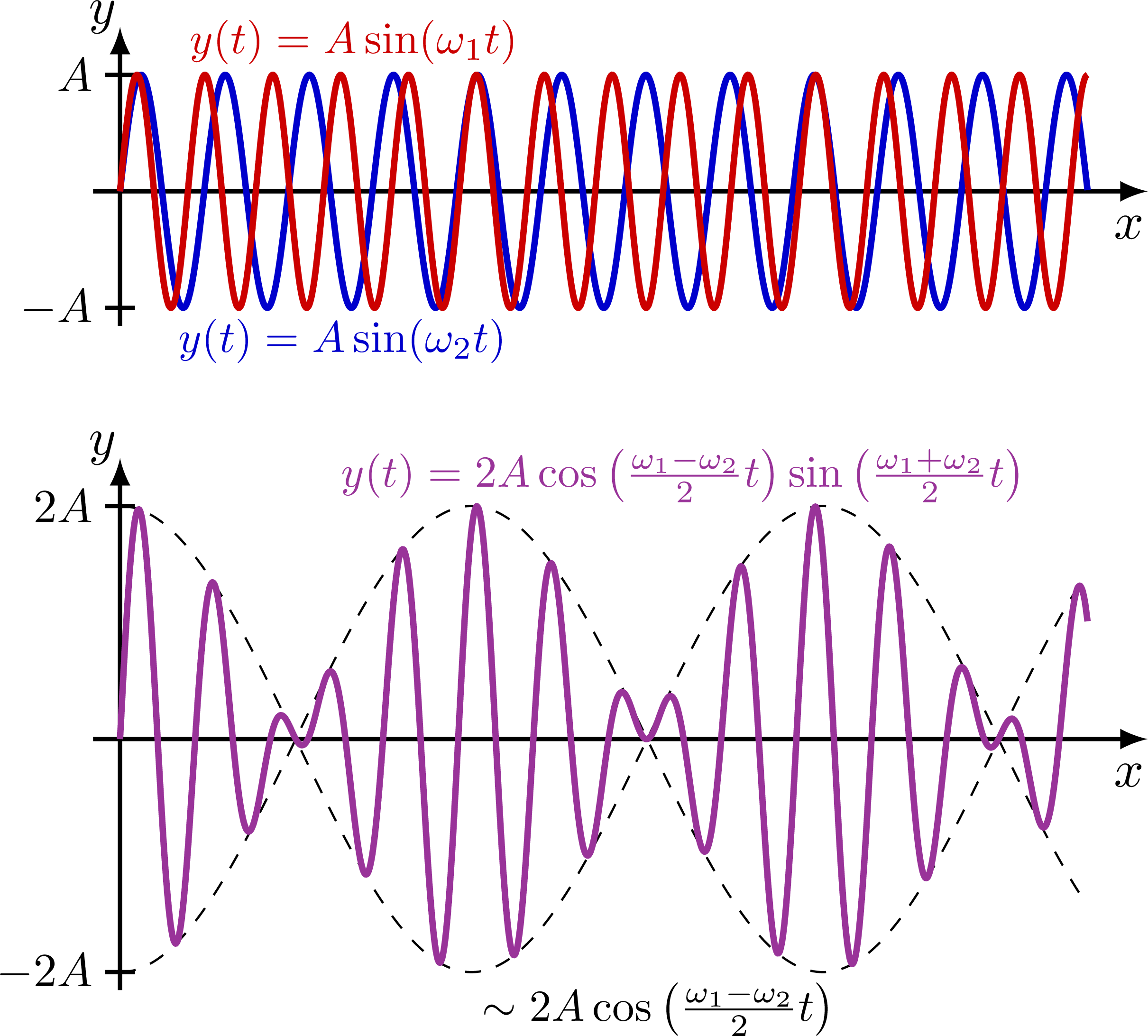Small difference in wavelength: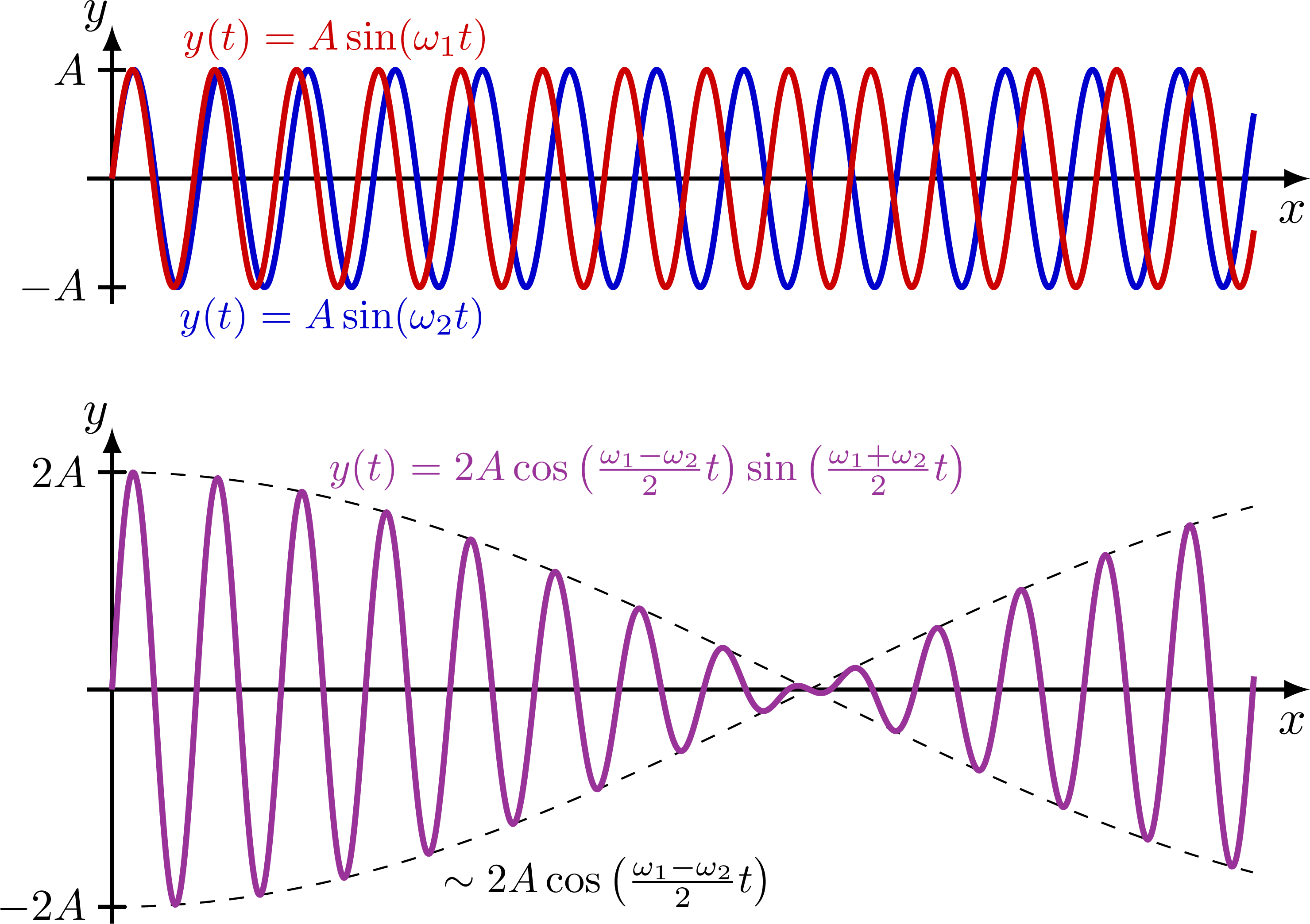

Edit and compile if you like:

% Author: Izaak Neutelings (December 2020)
\documentclass[border=3pt,tikz]{standalone}
\usepackage{amsmath}
\usepackage{etoolbox} % ifthen
\usepackage{tikz}
\usetikzlibrary{arrows.meta} % for arrow size
\tikzset{>=latex} % for LaTeX arrow head

\colorlet{xcol}{blue!70!black}
\colorlet{vcol}{green!60!black}
\colorlet{myred}{red!80!black}
\colorlet{myblue}{blue!80!black}
\colorlet{mypurple}{blue!50!red!80}
\colorlet{metalcol}{blue!25!black!30!white}
\tikzstyle{vvec}=[->,vcol,very thick,line cap=round]
\tikzstyle{node}=[xcol,scale=0.8]
\tikzstyle{metal}=[draw=metalcol!10!black,rounded corners=0.1,
  top color=metalcol,bottom color=metalcol!80!black,shading angle=10]
\tikzstyle{ring}=[metalcol!20!black,double=metalcol!70!black,double distance=1.2,line width=0.3]
\tikzstyle{rope}=[brown!20!black,double=brown!70!black,
  double distance=1.2,line width=0.6] %very thick,line cap=round
\tikzstyle{wood}=[draw=brown!80!black,rounded corners=0.1,
  top color=brown!80,bottom color=brown!80!black!80,shading angle=10]
\def\tick#1#2{\draw[thick] (#1) ++ (#2:0.1) --++ (#2-180:0.2)}

\begin{document}

\def\xmax{6.48}
\def\ymax{0.9}
\def\A{0.78}   % amplitude
\def\s{4.7*\A} % shift
\def\N{400}    % number of points for plot
\def\fa{1.775} % wavelength 1
\def\fb{2.20}  % wavelength 2
\def\waves{

  % TWO WAVES
  \draw[->,thick] (-0.2*\ymax,0) -- (0.4+\xmax,0) node[right=4,below left=1] {$x$};
  \draw[->,thick] (0,-\ymax) -- (0,0.2+\ymax) node[below=2,above left=-3] {$y$};
  \tick{0,\A}{0} node[scale=0.9,left=-1] {$A$};
  \tick{0,-\A}{0} node[scale=0.9,left=-1] {$-A$};
  \draw[myblue,very thick,samples=\N,smooth,variable=\x,domain=0:\xmax]
    plot(\x,{\A*sin(360*\fa*\x)});
  \draw[myred,very thick,samples=\N,smooth,variable=\x,domain=0:\xmax]
    plot(\x,{\A*sin(360*\fb*\x)});
  %\draw[vvec] (1.3/\fa,0.55*\A) --++ (0.38/\fa,0) node[above=1,right=-2] {$v$};
  
  % BEAT
  \begin{scope}[shift={(0,-\s)}]
    \draw[->,thick] (-0.2*\ymax,0) -- (0.4+\xmax,0) node[right=4,below left=1] {$x$};
    \draw[->,thick] (0,-\ymax-\A) -- (0,0.2+\ymax+\A) node[below=2,above left=-3] {$y$};
    \tick{0,2*\A}{0} node[scale=0.9,left=-1] {$2A$};
    \tick{0,-2*\A}{0} node[scale=0.9,left=-1] {$-2A$};
    \draw[dashed,samples=2*\N,smooth,variable=\x,domain=0:\xmax]
      plot(\x,{ 2*\A*cos(180*(\fa-\fb)*\x)})
      plot(\x,{-2*\A*cos(180*(\fa-\fb)*\x)});
    \draw[mypurple,very thick,samples=\N,smooth,variable=\x,domain=0:\xmax]
      plot(\x,{ 2*\A*sin(180*(\fa+\fb)*\x)*cos(180*(\fa-\fb)*\x)});
    %\node[above right=-1,mypurple,scale=0.85] at ({5.6/(\fa+\fb)},1.94*\A)
    %  {$y(t)=2A\sin\left(\frac{\omega_1+\omega_2}{2}t\right)\cos\left(\frac{\omega_1-\omega_2}{2}t\right)$};
    %\node[below right=-1,scale=0.85] at ({1/(\fb-\fa)},-2*\A)
    %  {$\sim2A\cos\left(\frac{\omega_1-\omega_2}{2}t\right)$};
  \end{scope}
}

% BEAT small
\begin{tikzpicture}
  \waves
  \node[above right=-1,myred,scale=0.85] at (0.7/\fa,\A) {$y(t)=A\sin(\omega_1 t)$};
  \node[below right=-1,myblue,scale=0.85] at (0.7/\fb,-\A) {$y(t)=A\sin(\omega_2 t)$};
  \begin{scope}[shift={(0,-\s)}]
    \node[above right=-1,mypurple,scale=0.85] at ({5.6/(\fa+\fb)},1.94*\A)
      {$y(t)=2A\cos\left(\frac{\omega_1-\omega_2}{2}t\right)\sin\left(\frac{\omega_1+\omega_2}{2}t\right)$};
    \node[below right=-1,scale=0.85] at ({1/(\fb-\fa)},-2*\A)
      {$\sim2A\cos\left(\frac{\omega_1-\omega_2}{2}t\right)$};
  \end{scope}
\end{tikzpicture}

% BEAT large
\begin{tikzpicture}
  \def\xmax{8.19}
  \def\fa{1.6} % wavelength 1
  \def\fb{1.7} % wavelength 2
  \waves
  \node[above right=-1,myred,scale=0.85] at (0.7/\fa,\A) {$y(t)=A\sin(\omega_1 t)$};
  \node[below right=-1,myblue,scale=0.85] at (0.7/\fb,-\A) {$y(t)=A\sin(\omega_2 t)$};
  \begin{scope}[shift={(0,-\s)}]
    \node[above right=-1,mypurple,scale=0.85] at ({4.9/(\fa+\fb)},1.7*\A)
      {$y(t)=2A\cos\left(\frac{\omega_1-\omega_2}{2}t\right)\sin\left(\frac{\omega_1+\omega_2}{2}t\right)$};
    \node[below right=-1,scale=0.85] at ({0.23/(\fb-\fa)},-1.45*\A)
      {$\sim2A\cos\left(\frac{\omega_1-\omega_2}{2}t\right)$};
  \end{scope}
\end{tikzpicture}


\end{document}