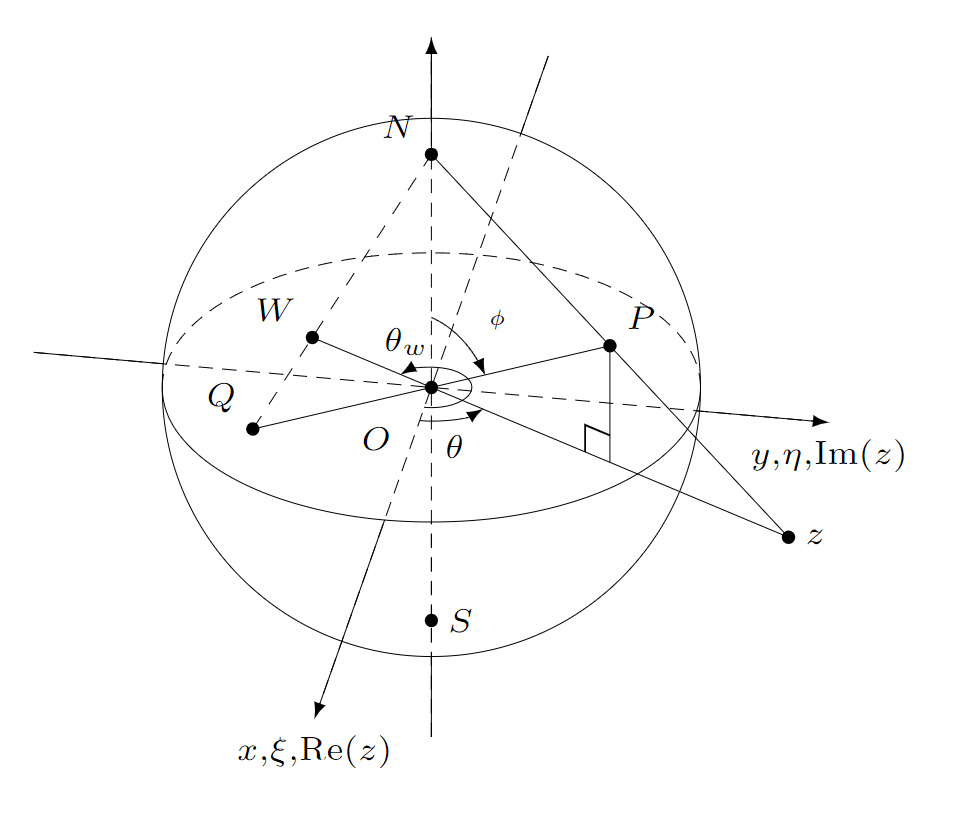
The stereographic projection of two antipodal points:
\documentclass[
tikz
,border = 3.14mm
]{standalone}
\usepackage{tikz-3dplot}
\usetikzlibrary{
arrows.meta
,angles
}
\pgfmathdeclarefunction{sphereX}{2}{%
% #1 - longitude
% #1 - latitude
\pgfmathparse{cos(#2) * cos(#1)}%
}
\pgfmathdeclarefunction{sphereY}{2}{%
\pgfmathparse{cos(#2) * sin(#1)}%
}
\pgfmathdeclarefunction{sphereZ}{2}{%
\pgfmathparse{sin(#2)}%
}
\pgfmathdeclarefunction{stereographicprojection}{2}{%
\pgfmathparse{#1 / (1 - #2)}%
}
\pgfmathsetmacro{\azimuth}{100}
\pgfmathsetmacro{\elevation}{30}
\pgfmathsetmacro{\longitude}{60}
\pgfmathsetmacro{\latitude}{30}
\begin{document}
\pgfmathsetmacro{\scale}{2}
\tdplotsetmaincoords{90-\elevation}{\azimuth}
\begin{tikzpicture}[tdplot_main_coords,very thin]
% x, y and z axes (pre-clip)
\draw[-latex]
(-2.5*\scale,0,0) -- (2.5*\scale,0,0)
node[pos=1,below]
{$\scriptstyle x,\xi,\mbox{\scriptsize Re}(z)$};
\draw[-latex]
(0,-1.5*\scale,0) -- (0,1.5*\scale,0);
\draw[-latex]
(0,0,-1.5*\scale) -- (0,0,1.5*\scale);
\begin{scope}
% clip and blank out sphere
\clip[
tdplot_screen_coords
,postaction = {
%tdplot_screen_coords
,fill
,white
}
] (0,0) circle [radius = {1*\scale}];
% x, y and z axes (post-clip)
\draw[densely dashed]
(-2.5*\scale,0,0) -- (1*\scale,0,0);
\draw[densely dashed]
(0,-1.5*\scale,0) -- (0,1*\scale,0);
\draw[densely dashed]
(0,0,-1.5*\scale) -- (0,0,1*\scale);
% outer circle
\draw[tdplot_screen_coords]
(0,0) circle [radius = {1*\scale}];
\draw[densely dashed]
(\azimuth:1*\scale) arc [
start angle = {\azimuth}
,end angle = {\azimuth+180}
,radius = {1*\scale}
];
\draw (\azimuth:1*\scale) arc [
start angle = {\azimuth}
,end angle = {\azimuth-180}
,radius = {1*\scale}
];
% origin
\coordinate (O) at (0,0);
% point on sphere
\coordinate (P) at
(
{sphereX(\longitude,\latitude)*\scale}
,{sphereY(\longitude,\latitude)*\scale}
,{sphereZ(\longitude,\latitude)*\scale}
);
% stereographic projection
% of point on sphere
\coordinate (P') at
(
{
stereographicprojection(
sphereX(\longitude,\latitude)
,sphereZ(\longitude,\latitude)
)*\scale
}
,{
stereographicprojection(
sphereY(\longitude,\latitude)
,sphereZ(\longitude,\latitude)
)*\scale
}
,{0}
);
% north pole
\coordinate (N) at (0,0,1*\scale);
% south pole
\coordinate (S) at (0,0,-1*\scale);
% point opposite from P
\coordinate (Q) at
(
{-sphereX(\longitude,\latitude)*\scale}
,{-sphereY(\longitude,\latitude)*\scale}
,{-sphereZ(\longitude,\latitude)*\scale}
);
% stereographic projection of
% point opposite from P
\coordinate (Q') at
(
{
stereographicprojection(
-sphereX(\longitude,\latitude)
,-sphereZ(\longitude,\latitude)
)*\scale
}
,{
stereographicprojection(
-sphereY(\longitude,\latitude)
,-sphereZ(\longitude,\latitude)
)*\scale
}
,{0}
);
% orthogonal projection of
% P onto the xy plane
\coordinate (projP) at
(
{sphereX(\longitude,\latitude)*\scale}
,{sphereY(\longitude,\latitude)*\scale}
,{0}
);
% constructions which don't exceed the clip
\draw
(P) -- (Q)
(N) -- (0,0,1.5*\scale)
(1*\scale,0,0) -- (2.5*\scale,0,0)
(0,1*\scale,0) -- (0,1.5*\scale,0)
(P) -- (projP)
;
\draw[densely dashed]
(N) -- (Q);
\end{scope}
% constructions which exceed the clip
\draw
(N) -- (P')
(Q') -- (P')
;
% points
\pgfmathsetmacro{\pointradius}{0.025*\scale}
\begin{scope}[tdplot_screen_coords]
\fill
(O) circle[radius = \pointradius]
node[below left=5pt]{$\scriptstyle O$};
\fill
(P) circle[radius = \pointradius]
node[above right]{$\scriptstyle P$};
\fill
(P') circle[radius = \pointradius]
node[right]{$\scriptstyle z$};
\fill
(N) circle[radius = \pointradius]
node[above left]{$\scriptstyle N$};
\fill
(S) circle[radius = \pointradius]
node[right]{$\scriptstyle S$};
\fill
(Q) circle[radius = \pointradius]
node[above left]{$\scriptstyle Q$};
\fill
(Q') circle[radius = \pointradius]
node[above left]{$\scriptstyle W$};
\end{scope}
% angles
\draw[-latex]
(0.25*\scale,0) arc [
start angle = {0}
,end angle = {\longitude}
,radius = {0.25*\scale}
]
node [
pos = {0.5}
,below
] {$\scriptstyle\theta$};
\draw[-latex]
(0.15*\scale,0) arc [
start angle = {0}
,end angle = {\longitude + 180}
,radius = {0.15*\scale}
] node [
pos = 0.95
,above
]{$\scriptstyle\theta_{w}$};
\draw[
smooth
,domain = {90:\latitude}
,variable = {\latitude}
,-latex
] plot (
{0.3*sphereX(\longitude,\latitude)*\scale}
,{0.3*sphereY(\longitude,\latitude)*\scale}
,{0.3*sphereZ(\longitude,\latitude)*\scale}
) node [
pos = {0}
,above right = {5pt}
]{$\scriptstyle\phi$};
\draw pic [
draw
,-
,angle eccentricity = {1.4}
,angle radius = {0.2cm}
]{right angle=O--projP--P};
\end{tikzpicture}
\end{document}


