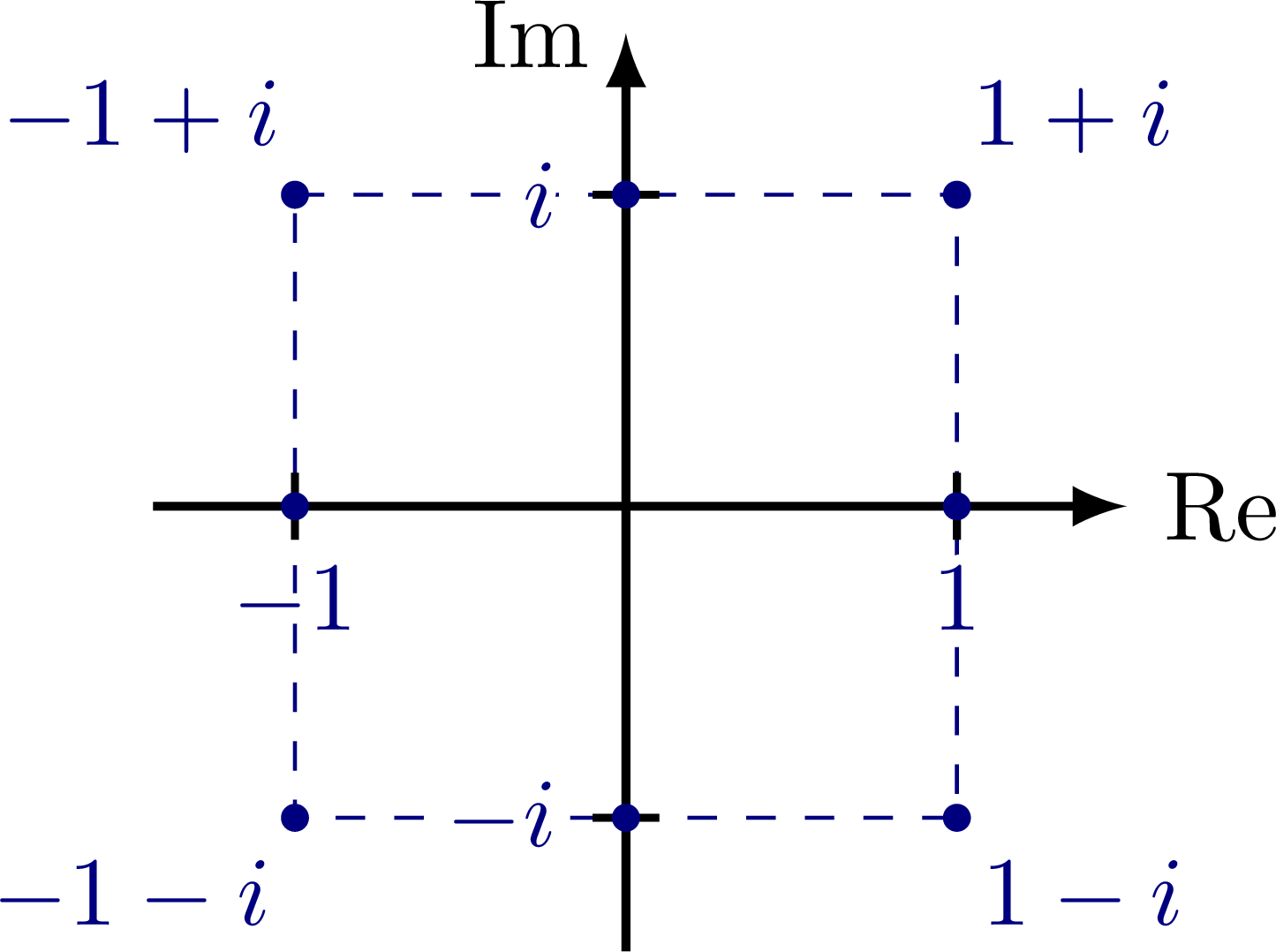
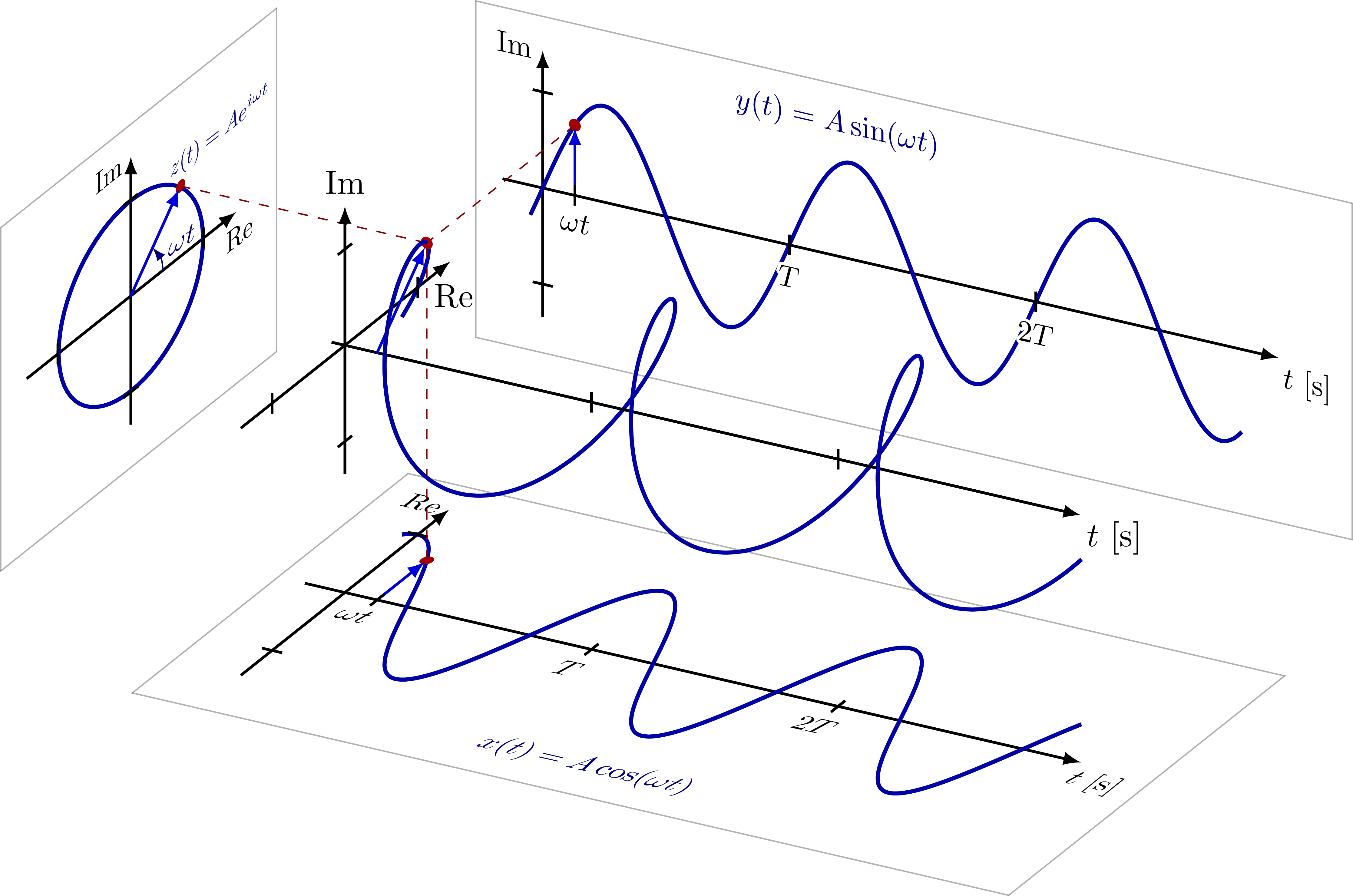
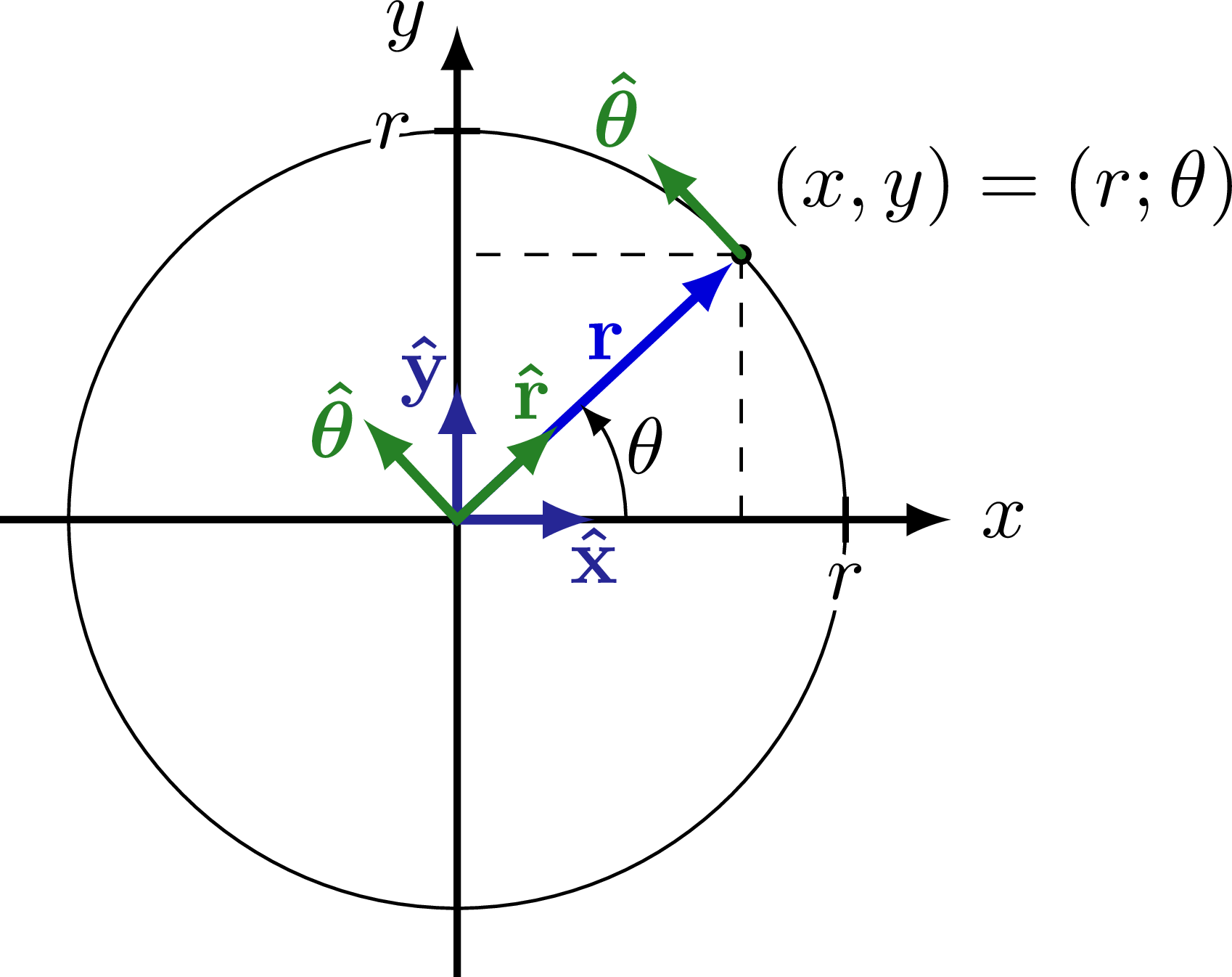
Complex plane with the imaginary and real axis, complex conjugation, polar coordinates, Euler’s formula, phasor, analytic representation of harmonic oscillators (helix), and rotation of a complex number in the complex or 2D real plane (comparing SO(2) and U(1)). Also have a look at the rotation matrix.
Edit and compile if you like:
% Author: Izaak Neutelings (January 2021)
\documentclass[border=3pt,tikz]{standalone}
\usepackage{amsmath}
\usepackage{tikz}
\usepackage{physics}
\usepackage[outline]{contour} % glow around text
%\usetikzlibrary{intersections}
%\usetikzlibrary{decorations.markings}
\usetikzlibrary{angles,quotes} % for pic
\usetikzlibrary{bending} % for arrow head angle
\contourlength{1.0pt}
\usetikzlibrary{3d}
\tikzset{>=latex} % for LaTeX arrow head
\usepackage{xcolor}
\colorlet{myblue}{blue!65!black}
\colorlet{mydarkblue}{blue!50!black}
\colorlet{myred}{red!65!black}
\colorlet{mydarkred}{red!40!black}
\colorlet{veccol}{green!70!black}
\colorlet{vcol}{green!70!black}
\colorlet{xcol}{blue!85!black}
%\colorlet{projcol}{xcol!60}
%\colorlet{unitcol}{xcol!60!black!85}
%\colorlet{myred}{red!90!black}
%\colorlet{mypurple}{blue!50!red!80!black!80}
\tikzstyle{vector}=[->,very thick,xcol,line cap=round]
\tikzstyle{xline}=[myblue,very thick]
\tikzstyle{yzp}=[canvas is zy plane at x=0]
\tikzstyle{xzp}=[canvas is xz plane at y=0]
\tikzstyle{xyp}=[canvas is xy plane at z=0]
\def\tick#1#2{\draw[thick] (#1) ++ (#2:0.12) --++ (#2-180:0.24)}
\def\N{100}
\begin{document}
% COMPLEX
\begin{tikzpicture}
\def\xmax{2.0}
\def\ymax{1.6}
\def\R{1.9}
\def\ang{35}
\coordinate (O) at (0,0);
\coordinate (R) at (\ang:\R);
\coordinate (-R) at (-\ang:\R);
\coordinate (X) at ({\R*cos(\ang)},0);
\coordinate (Y) at (0,{\R*sin(\ang)});
\coordinate (-Y) at (0,{-\R*sin(\ang)});
\node[fill=mydarkblue,circle,inner sep=0.8] (R') at (R) {};
\node[fill=mydarkred,circle,inner sep=0.8] (-R') at (-R) {};
\node[mydarkblue,above right=-2] at (R') {$z=x+iy=re^{i\theta}$};
\node[mydarkred,below right=-1] at (-R') {$\overline{z}=x-iy=re^{-i\theta}$};
\draw[dashed,mydarkblue]
(Y) -- (R') --++ (0,{0.1-\R*sin(\ang)});
\draw[dashed,mydarkred]
(-Y) -- (-R') --++ (0,{\R*sin(\ang)-0.45});
\draw[->,line width=0.9] (-0.65*\xmax,0) -- (\xmax+0.05,0) node[right] {Re};
\draw[->,line width=0.9] (0,-\ymax) -- (0,\ymax+0.05) node[left] {Im};
\draw[vector] (O) -- (R') node[pos=0.55,above left=-2] {$r$};
\draw[vector,myred] (O) -- (-R') node[pos=0.55,below left=-2] {$r$};
\draw pic[->,"$\theta$",mydarkblue,draw=mydarkblue,angle radius=23,angle eccentricity=1.24]
{angle = X--O--R};
\draw pic[<-,"$-\theta$"{right=-1},mydarkred,draw=mydarkred,angle radius=20,angle eccentricity=1]
{angle = -R--O--X};
%\tick{X}{90} node[scale=0.9,left=6,below right=-2] {$x = r\cos\theta$};
\tick{X}{90} node[scale=1,below=-1] {$x$};
\tick{Y}{ 0} node[mydarkblue,scale=1,left] {$y$}; %r\sin\theta =
\tick{-Y}{ 0} node[mydarkred,scale=1,left] {$-y$};
\end{tikzpicture}
% COMPLEX numbers
\begin{tikzpicture}
\def\xmax{1.7}
\def\ymax{1.6}
\def\re{0.7*\xmax}
\def\im{0.7*\ymax}
\coordinate (O) at (0,0);
\draw[dashed,mydarkblue]
(-\re,\im) -| (\re,-\im) -| cycle;
\draw[->,line width=0.9] (-\xmax,0) -- (\xmax+0.1,0) node[right] {Re};
\draw[->,line width=0.9] (0,-\ymax) -- (0,\ymax+0.1) node[left] {Im};
\tick{\re,0}{90} node[mydarkblue,scale=1,below=-1] {\contour{white}{$1$}};
\tick{-\re,0}{90} node[mydarkblue,scale=1,below=-1] {\contour{white}{$-1$}};
\tick{0,\im}{ 0} node[mydarkblue,scale=1,left] {\contour{white}{$i$}}; %r\sin\theta =
\tick{0,-\im}{ 0} node[mydarkblue,scale=1,left] {\contour{white}{$-i$}};
\fill[mydarkblue]
( 0, \im) circle(0.05)
( 0,-\im) circle(0.05)
( \re, 0) circle(0.05)
(-\re, 0) circle(0.05)
( \re, \im) circle(0.05)
node[mydarkblue,scale=1,above right=-2] {\strut$1+i$}
( \re,-\im) circle(0.05)
node[mydarkblue,scale=1,below right=-1] {\strut$1-i$}
(-\re, \im) circle(0.05)
node[mydarkblue,scale=1,above left=-2] {\strut$-1+i$}
(-\re,-\im) circle(0.05)
node[mydarkblue,scale=1,below left=-1] {\strut$-1-i$};
\end{tikzpicture}
% COMPLEX OSCILLATOR
\begin{tikzpicture}
\def\xmax{2.2}
\def\ymax{2.2}
\def\R{1.8}
\def\ang{35}
\coordinate (O) at (0,0);
\coordinate (R) at (\ang:\R);
\coordinate (X) at ({\R*cos(\ang)},0);
\coordinate (Y) at (0,{\R*sin(\ang)});
\draw[xline] (O) circle (\R); %0.995*\R
\node[fill=myred,circle,inner sep=1] (R') at (R) {};
\node[mydarkblue,above right=0] at (R') {$z(t)=Ae^{i\omega t}$};
\draw[dashed,mydarkblue]
(Y) -- (R') --++ (0,{0.1-\R*sin(\ang)});
\draw[->,line width=0.9] (-\xmax,0) -- (\xmax+0.05,0) node[right] {Re};
\draw[->,line width=0.9] (0,-\ymax) -- (0,\ymax+0.05) node[left] {Im};
\draw[vector] (O) -- (R') node[pos=0.55,above left=-2] {$A$};
\draw pic[->,"$\omega t$",mydarkblue,draw=mydarkblue,angle radius=22,angle eccentricity=1.4]
{angle = X--O--R};
\tick{0,\R+0.015}{0}; %node[scale=0.9,left=2] {\contour{white}{$R$}};
\tick{\R+0.015,0}{90}; %node[scale=0.9,right=1,below=0] {\contour{white}{$R$}};
\tick{0,-\R-0.015}{0};
\tick{-\R-0.015,0}{90};
\tick{X}{90} node[scale=0.9,left=14,below=-1] {$A\cos(\omega t)$}; %{\contour{white}{$A\cos(\omega t)$}};
\tick{Y}{ 0} node[scale=0.9,below=1,left=-2] {$A\sin(\omega t)$}; % {\contour{white}{$A\sin(\omega t)$}};
\end{tikzpicture}
% COMPLEX OSCILLATOR 3D
\def\xang{-13}
\def\zang{45}
\begin{tikzpicture}[x=(\xang:0.9), y=(90:0.9), z=(\zang:1.1)]
\message{^^JSynthesis 3D}
\def\xmax{8.8} % max x axis
\def\ymin{-1.5} % min y axis
\def\ymax{1.6} % max y axis
\def\zmax{1.6} % max z axis
\def\xf{1.17*\xmax} % x position frequency axis
\def\A{(0.70*\ymax)} % amplitude
\def\T{(0.335*\xmax)} % period
\def\w{\zmax/11.2} % spacing components
\def\ang{47} % angle
\def\s{\ang/360*\T} % time component
\def\x{\A*cos(\ang)} % real component
\def\y{\A*sin(\ang)} % imaginary component
% COMPLEX PLANE
\begin{scope}[shift={(-1.6*\zmax,0,0)}]
\draw[black,fill=white,opacity=0.3,yzp]
(-1.25*\zmax,-1.25*\ymax) rectangle (1.4*\zmax,1.25*\ymax);
\draw[->,thick] (0,\ymin,0) -- (0,\ymax+0.02,0)
node[pos=1,left=0,yzp] {Im};
\draw[->,thick] (0,0,-\zmax) -- (0,0,\zmax+0.02)
node[right=1,below=0,yzp] {Re} coordinate (X);
%\node[scale=1,yzp] at (0,-\ymax,0) {Complex plane};
\draw[xline,yzp] (0,0) circle(0.991*\A) coordinate (O);
\fill[myred,yzp] (\ang:{\A}) circle(0.07) coordinate(P);
\node[mydarkblue,above=3,right=-5,yzp,scale=0.8] at (P) {$z(t)=Ae^{i\omega t}$};
\draw[vector,thick,yzp] (0,0) -- (\ang:{\A-0.03}) coordinate (R);
\draw pic[-{>[flex'=1]},draw=mydarkblue,angle radius=14,angle eccentricity=1,
"$\omega t$"{above=0,right=-0.5,yslant=0.69,scale=0.8},mydarkblue,yzp]
{angle = X--O--R};
\tick{0,0,{\A}}{90};
\tick{0,0,{-\A}}{90};
\tick{0,{\A},0}{\zang};
\tick{0,{-\A},0}{\zang};
\end{scope}
% IMAGINARY
\begin{scope}[shift={(0,0,1.9*\zmax)}]
\draw[black,fill=white,opacity=0.3,xyp]
(-0.5*\ymax,-1.2*\ymax) rectangle (1.10*\xmax,1.25*\ymax);
\draw[->,thick] (-0.3*\ymax,0,0) -- (\xmax,0,0)
node[below right=-2,xyp] {$t$ [s]};
\draw[->,thick] (0,\ymin,0) -- (0,\ymax,0)
node[left,xyp] {Im};
\draw[xline,samples=\N,smooth,variable=\t,domain=-0.05*\T:0.95*\xmax]
plot(\t,{\A*sin(360/\T*\t)},0);
%\node[below=0,xyp] at (0.4*\xmax,-\ymax,0) {Imaginary component};
\fill[myred,xyp] ({\s},{\y}) circle(0.07) coordinate(I);
\draw[vector,thick,xyp] ({\s},0) --++ (0,{\y-0.03});
\tick{0,{\A},0}{180};
\tick{0,{-\A},0}{180};
\tick{{\s},0,0}{90} node[right=0,below=-1,xyp] {$\omega t$};
\tick{{\T},0,0}{90} node[right=0,below,xyp] {\contour{white}{$T$}};
\tick{{2*\T},0,0}{90} node[right=0,below,xyp] {\contour{white}{$2T$}};
\node[mydarkblue,below=0,xyp] at (0.4*\xmax,1.15*\ymax,0) {$y(t)=A\sin(\omega t)$};
\end{scope}
% REAL
\begin{scope}[shift={(0,-1.8*\zmax,0)}]
\draw[black,fill=white,opacity=0.3,xzp]
(-0.5*\ymax,-1.4*\ymax) rectangle (1.10*\xmax,1.25*\ymax);
\draw[->,thick] (-0.3*\ymax,0,0) -- (\xmax,0,0)
node[below right=-1,xzp] {$t$ [s]};
\draw[->,thick] (0,0,-\zmax) -- (0,0,\zmax)
node[left=-1,xzp] {Re};
\draw[xline,samples=\N,smooth,variable=\t,domain=-0.05*\T:0.95*\xmax]
plot(\t,0,{\A*cos(360/\T*\t)});
%\node[below=0,xzp] at (0.4*\xmax,-\ymax,0) {Real component};
\fill[myred,xzp] ({\s},{\x}) circle(0.07) coordinate(R);
\draw[vector,thick,xzp] ({\s},0) --++ (0,{\x-0.03});
\tick{0,0,{\A}}{180};
\tick{0,0,{-\A}}{180};
\tick{{\s},0,0}{\zang} node[below=-1,xzp] {$\omega t$};
\tick{{\T},0,0}{\zang} node[below,xzp] {$T$};
\tick{{2*\T},0,0}{\zang} node[below,xzp] {$2T$};
\node[mydarkblue,above=0,xzp] at (0.3*\xmax,-\ymax,0) {$x(t)=A\cos(\omega t)$};
\end{scope}
% COMPONENTS
\draw[myred!80!black,dashed]
(P) -- ({\s},{\y},{\x})
(I) -- ({\s},{\y},{\x+0.05})
({\s},{\y-0.06},{\x}) -- (R);
\draw[->,black,thick] (-0.1*\ymax,0,0) -- (\xmax,0,0) node[below right=-2] {$t$ [s]};
\draw[->,black,thick] (0,\ymin,0) -- (0,\ymax+0.02,0) node[above] {Im};
\draw[->,black,thick] (0,0,-\zmax) -- (0,0,\zmax+0.02) node[right=1,below=3] {Re};
\foreach \i [evaluate={\tmin=max(-0.05*\T,(\i-0.05)*\T); \tmax=min(0.95*\xmax,(\i+1)*\T);}] in {0,...,2}{
%\draw[white,line width=1.2] (\tmin,0,0) -- (\tmax,0,0);
\draw[thick] (\tmin,0,0) -- (\tmax,0,0);
\draw[xline,samples=0.4*\N,smooth,variable=\t]
plot[domain=\tmin:\tmax](\t,{\A*sin(360/\T*\t)},{\A*cos(360/\T*\t)});
}
\draw[thick] (0,0,{0.9*\A}) -- (0,0,{\A});
\fill[myred] ({\s},{\y},{\x}) circle(0.07) coordinate(Z);
\draw[vector,thick] ({\s},0,0) --++ (0,{\y-0.03},{\x-0.03});
\draw[xline,samples=0.3*\N,smooth,variable=\t,domain=\s+0.03:\s+0.4*\T,line cap=round]
plot(\t,{\A*sin(360/\T*\t)},{\A*cos(360/\T*\t)});
\tick{{\T},0,0}{90};
\tick{{2*\T},0,0}{90};
\tick{0,0,{\A}}{90};
\tick{0,0,{-\A}}{90};
\tick{0,{\A},0}{\zang};
\tick{0,{-\A},0}{\zang};
\draw[myred!80!black,dashed]
({\s},{\y-0.06},{\x}) --++ (0,-0.2*\ymax,0);
\end{tikzpicture}
% VECTOR ROTATION
\def\xmax{2.7}
\def\ymax{2.7}
\def\R{2.3}
\def\ang{28}
\def\dang{35}
\begin{tikzpicture}
\coordinate (O) at (0,0);
\coordinate (R) at (\ang:\R);
\coordinate (Q) at (\ang+\dang:\R);
\coordinate (X) at ({\R*cos(\ang)},0);
\coordinate (Y) at (0,{\R*sin(\ang)});
\coordinate (X') at ({\R*cos(\ang+\dang)},0);
\coordinate (Y') at (0,{\R*sin(\ang+\dang)});
%\draw[myblue] (O) circle (0.995*\R);
\draw[myblue] (-10:\R) arc (-10:100:\R);
\node[fill=myred,circle,inner sep=0.8] at (R) {};
\node[fill=myred,circle,inner sep=0.8] at (Q) {};
\node[mydarkblue,above right=-2] at (R) {$\vb{r}=(x,y)$};
\node[mydarkblue,above right=-2] at (Q) {$\vb{r}'=(x',y')$};
\draw[dashed,mydarkblue]
(Y) -- (R) --++ (0,{0.1-\R*sin(\ang)});
\draw[dashed,mydarkblue]
(Y') -- (Q) --++ (0,{0.1-\R*sin(\ang+\dang)});
\draw[->,line width=0.9] (-0.1*\xmax,0) -- (\xmax+0.05,0) node[right] {$x$};
\draw[->,line width=0.9] (0,-0.1*\ymax) -- (0,\ymax+0.05) node[left] {$y$};
\draw[vector] (O) -- (R);
\draw[vector] (O) -- (Q);
\draw pic[->,"$\phi$",mydarkblue,draw=mydarkblue,angle radius=20,angle eccentricity=1.35]
{angle = R--O--Q};
\tick{0,\R+0.015}{0};
\tick{\R+0.015,0}{90};
\tick{X}{90} node[scale=0.9,left=0,below=-1] {$x$};
\tick{Y}{ 0} node[scale=0.9,below=1,left=-2] {$y$};
\tick{X'}{90} node[scale=0.9,left=0,below=-4] {$x'$};
\tick{Y'}{ 0} node[scale=0.9,below=1,left=-2] {$y'$};
\end{tikzpicture}
% COMPLEX ROTATION
\begin{tikzpicture}
\coordinate (O) at (0,0);
\coordinate (R) at (\ang:\R);
\coordinate (Q) at (\ang+\dang:\R);
\coordinate (X) at ({\R*cos(\ang)},0);
\coordinate (Y) at (0,{\R*sin(\ang)});
%\draw[myblue] (O) circle (0.995*\R);
\draw[myblue] (-10:\R) arc (-10:100:\R);
\node[fill=myred,circle,inner sep=0.8] at (R) {};
\node[fill=myred,circle,inner sep=0.8] at (Q) {};
\node[mydarkblue,above right=0] at (R) {$z=re^{i\theta}$};
\node[mydarkblue,left=2,above right=0] at (Q) {$ze^{i\phi}=re^{i(\theta+\phi)}$};
\draw[dashed,mydarkblue]
(Y) -- (R) --++ (0,{0.1-\R*sin(\ang)});
\draw[->,line width=0.9] (-0.1*\xmax,0) -- (\xmax+0.05,0) node[right] {Re};
\draw[->,line width=0.9] (0,-0.1*\ymax) -- (0,\ymax+0.05) node[left] {Im};
\draw[vector] (O) -- (R) node[pos=0.65,above left=-3] {$r$};
\draw[vector] (O) -- (Q) node[pos=0.65,above left=-3] {$r$};
\draw pic[->,"$\theta$",mydarkblue,draw=mydarkblue,angle radius=24,angle eccentricity=1.25]
{angle = X--O--R};
\draw pic[->,"$\phi$",mydarkblue,draw=mydarkblue,angle radius=20,angle eccentricity=1.35]
{angle = R--O--Q};
\tick{0,\R+0.015}{0};
\tick{\R+0.015,0}{90};
\tick{X}{90} node[scale=0.9,left=14,below=-1] {$r\cos\theta$};
\tick{Y}{ 0} node[scale=0.9,below=1,left=-2] {$r\sin\theta$};
\end{tikzpicture}
\end{document}Click to download: complex.tex • complex.pdf
Open in Overleaf: complex.tex



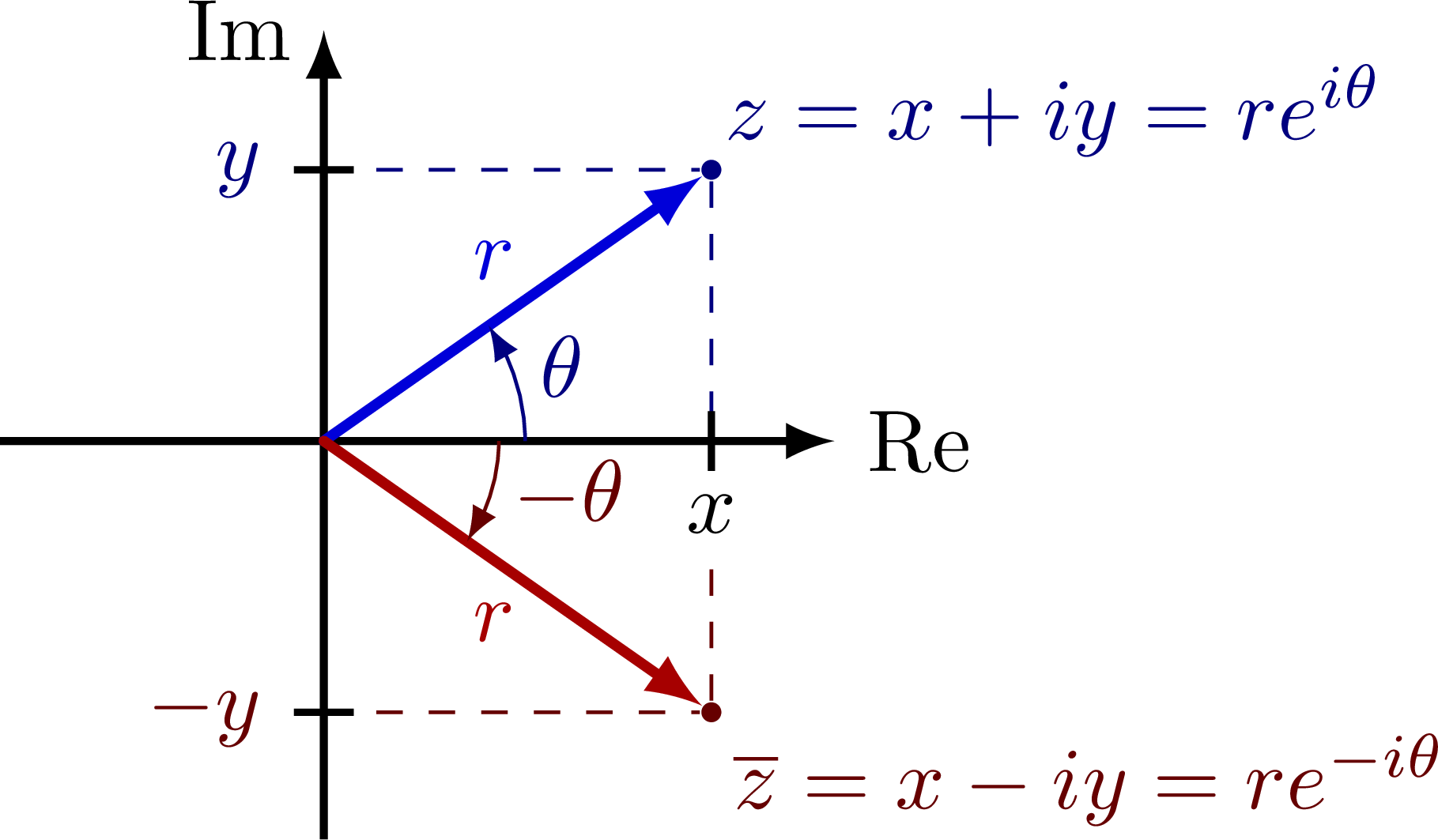
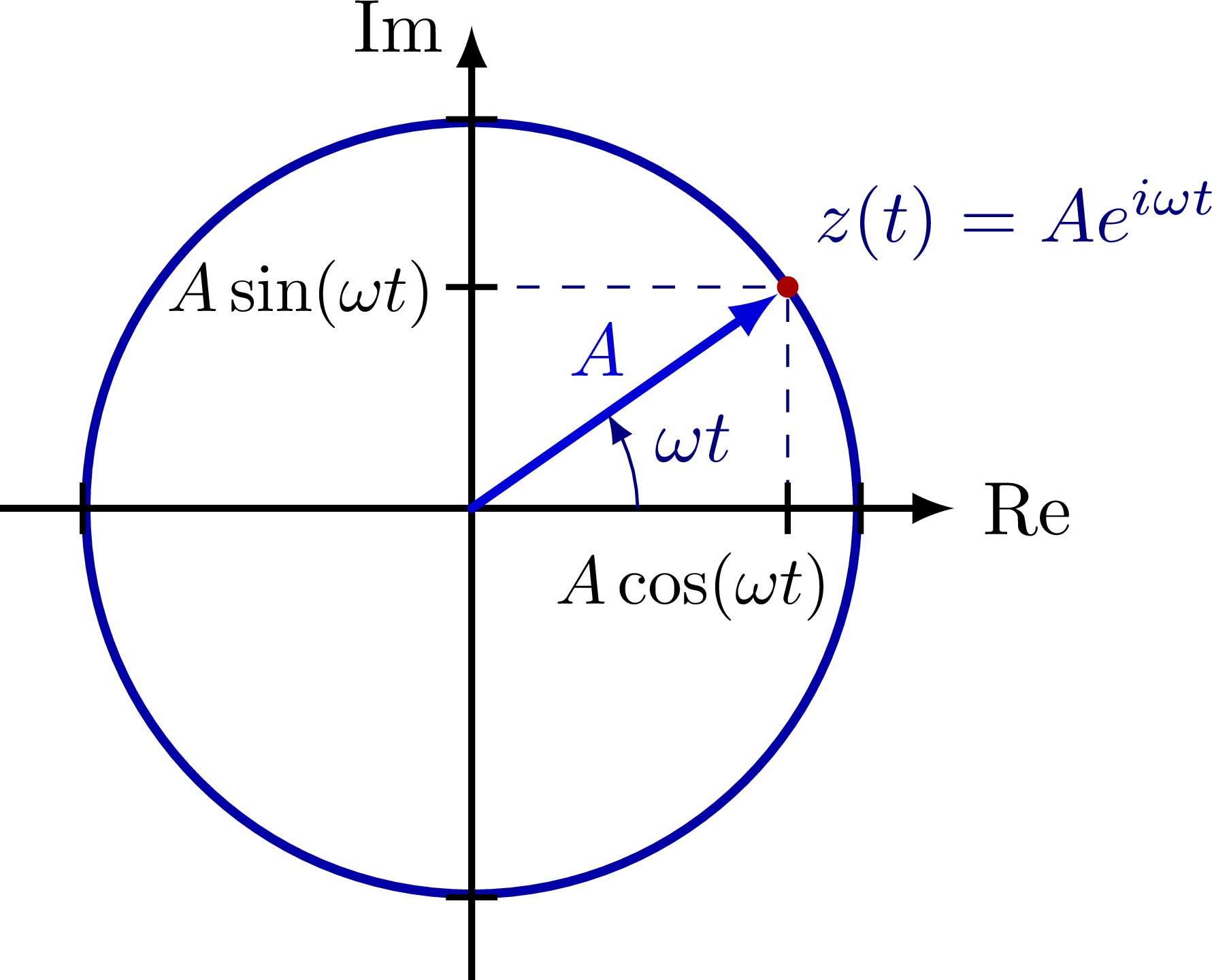

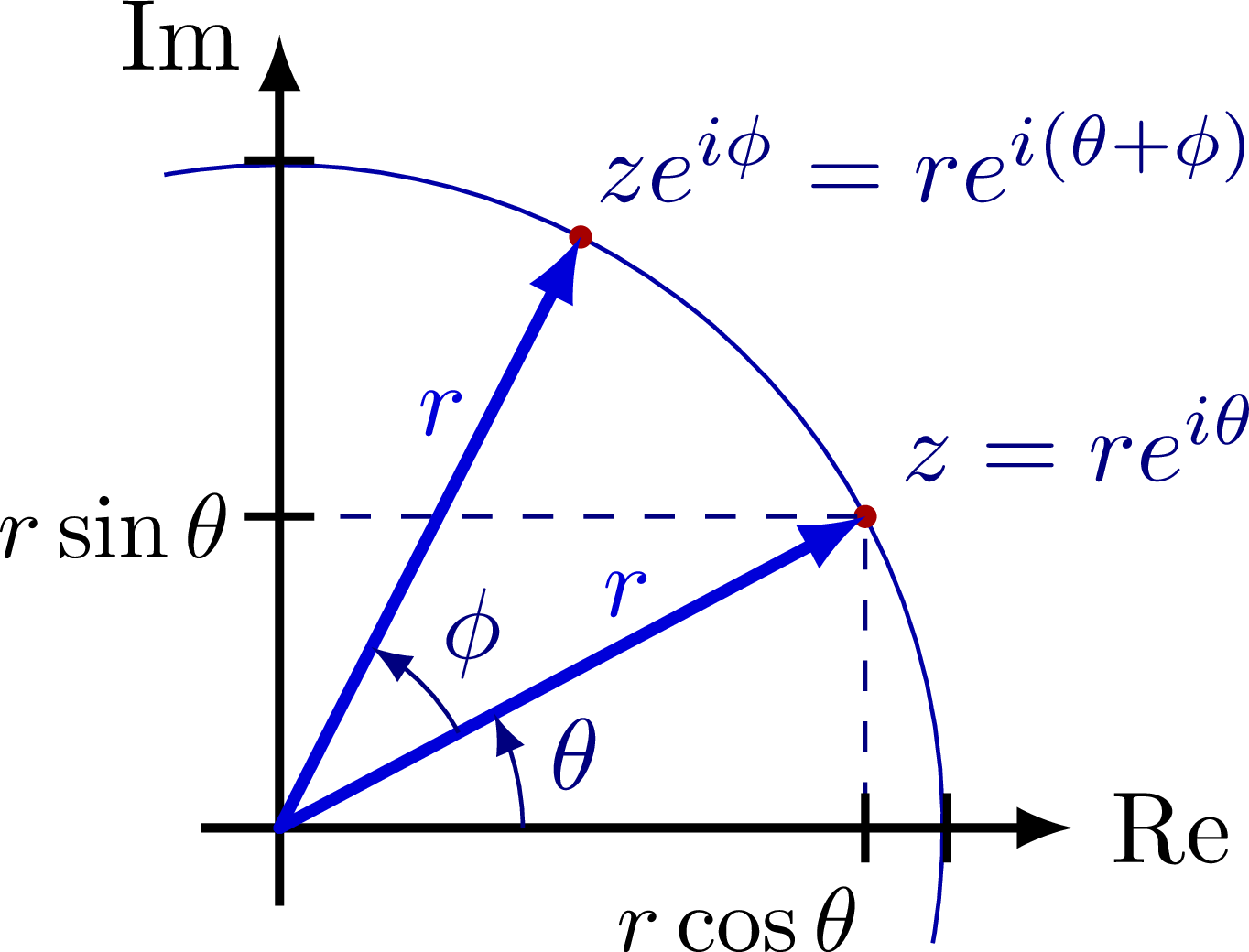

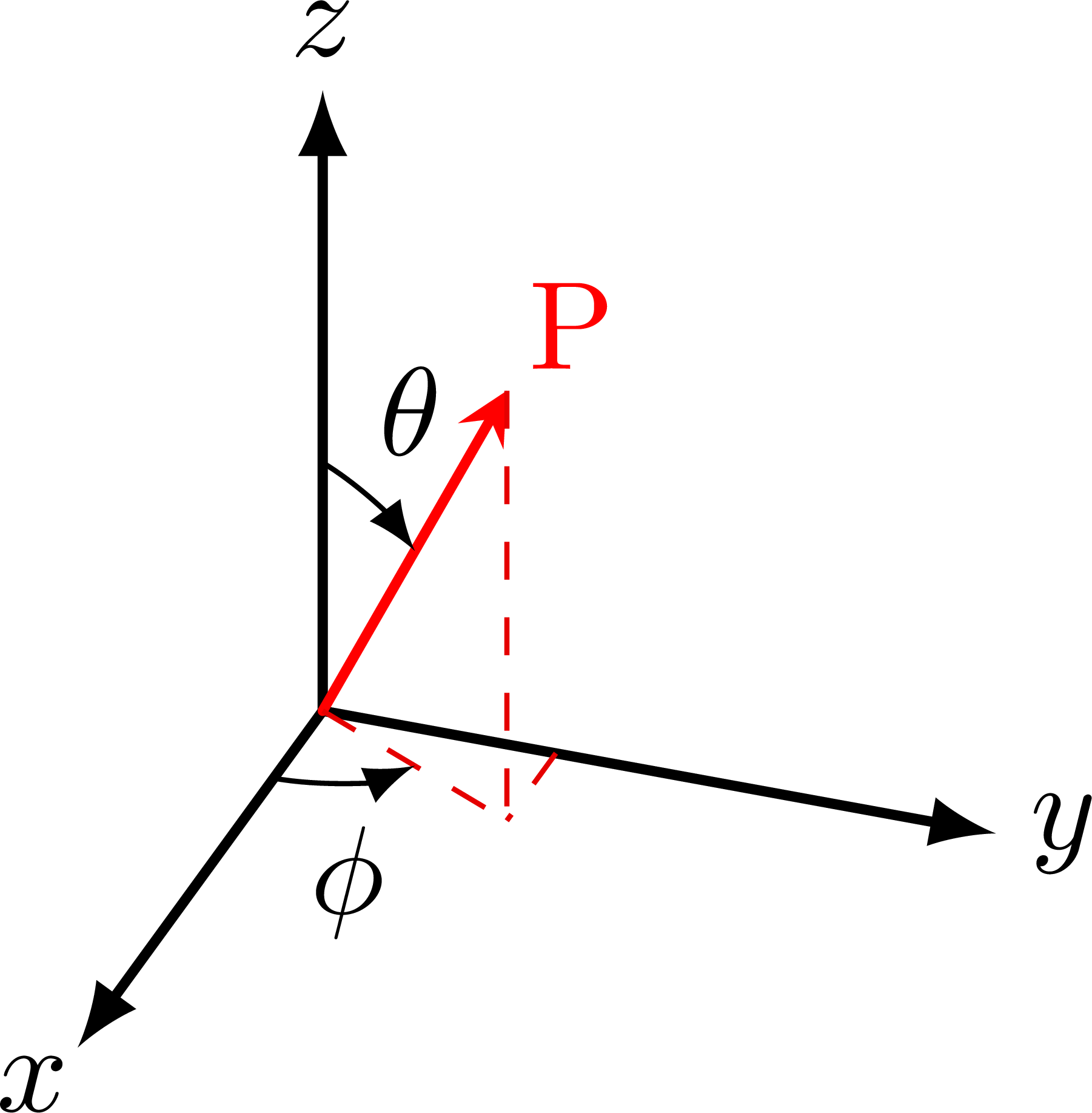
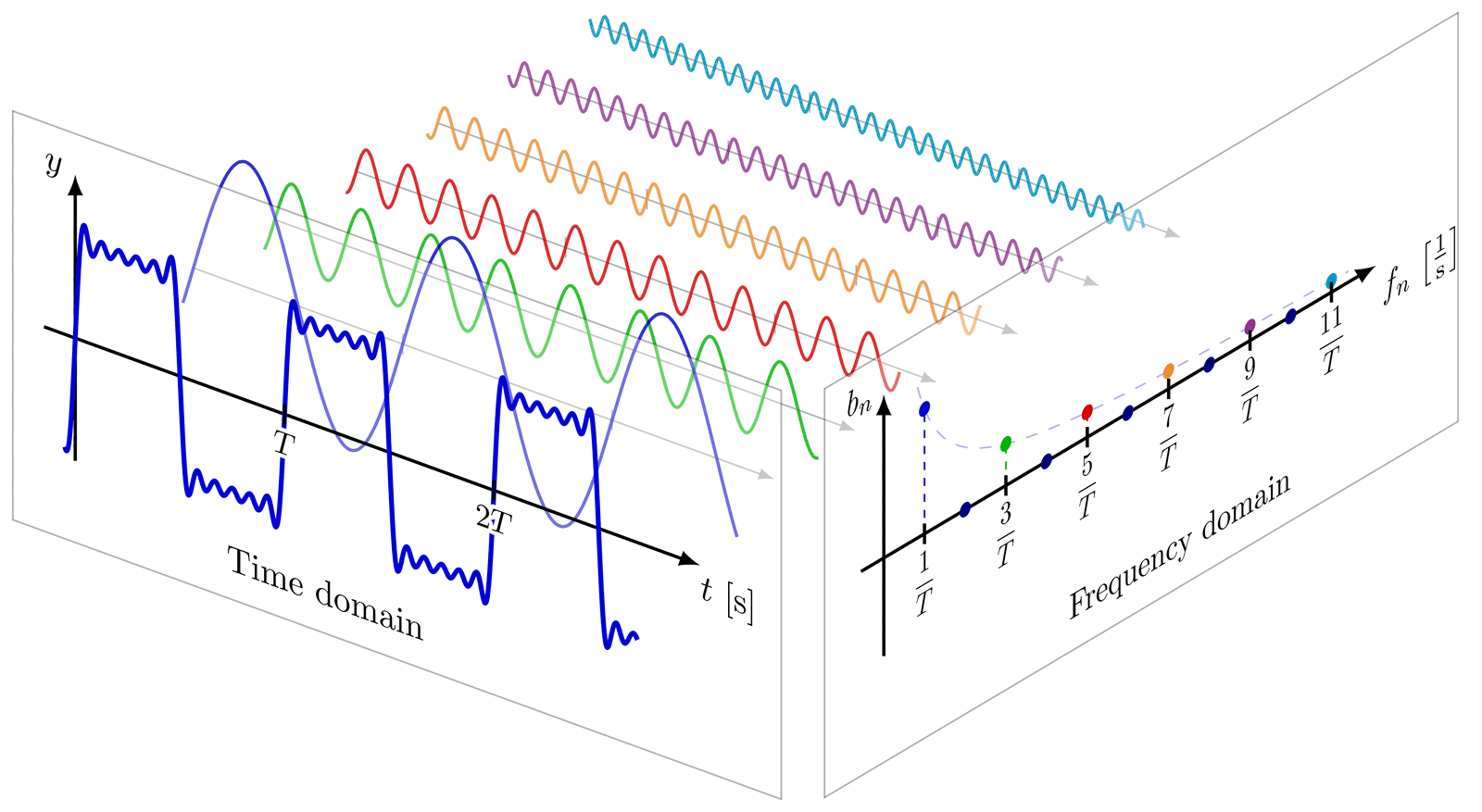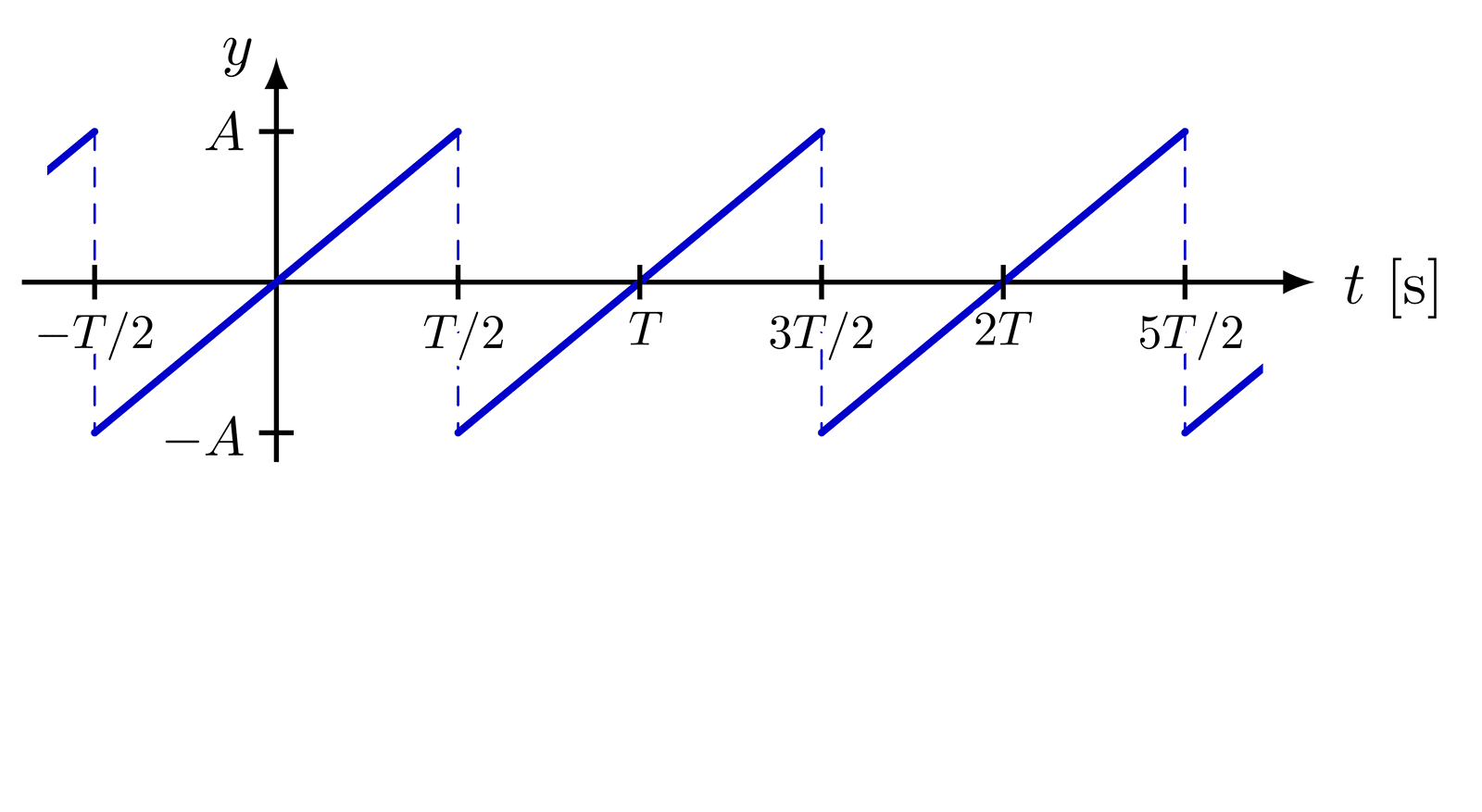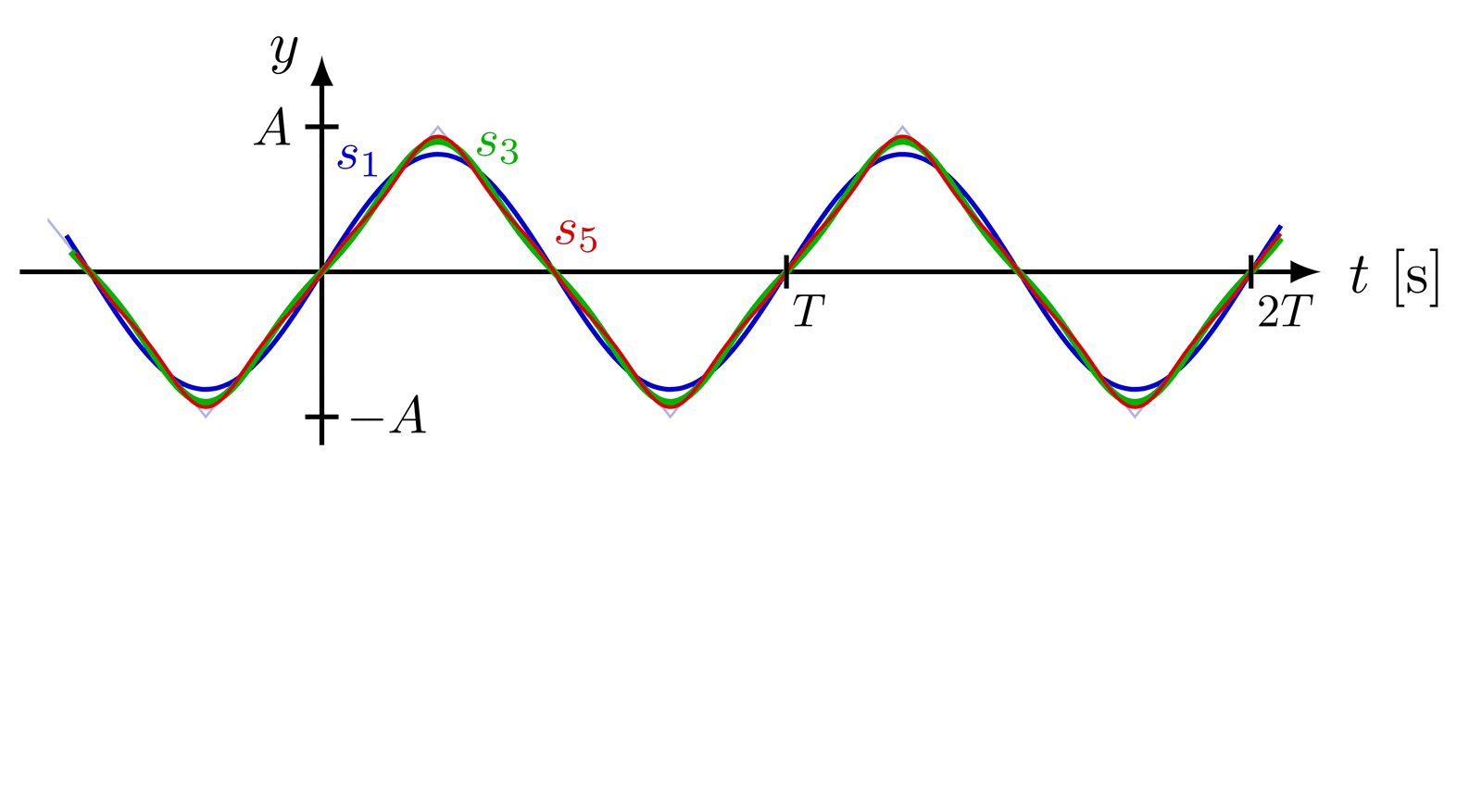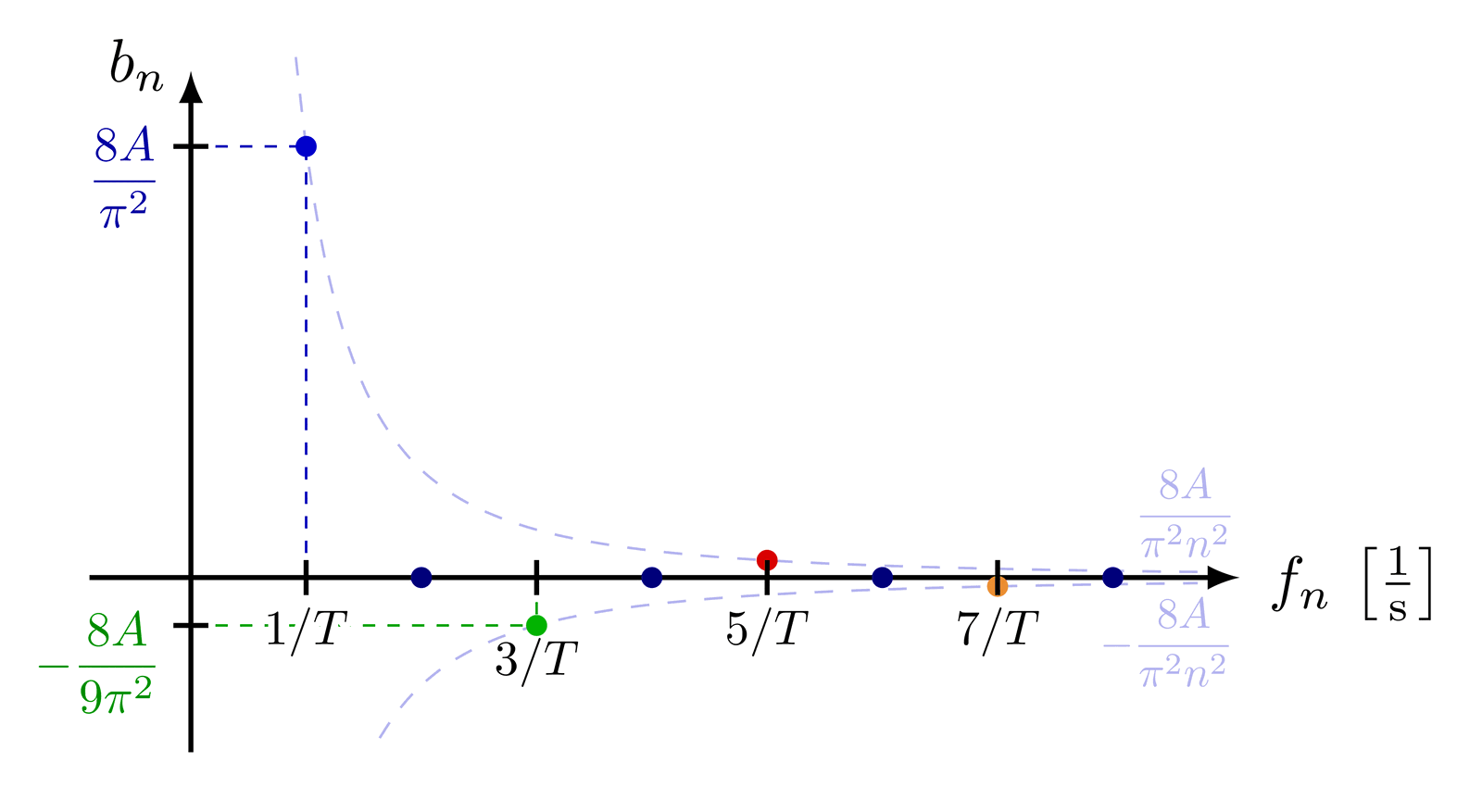
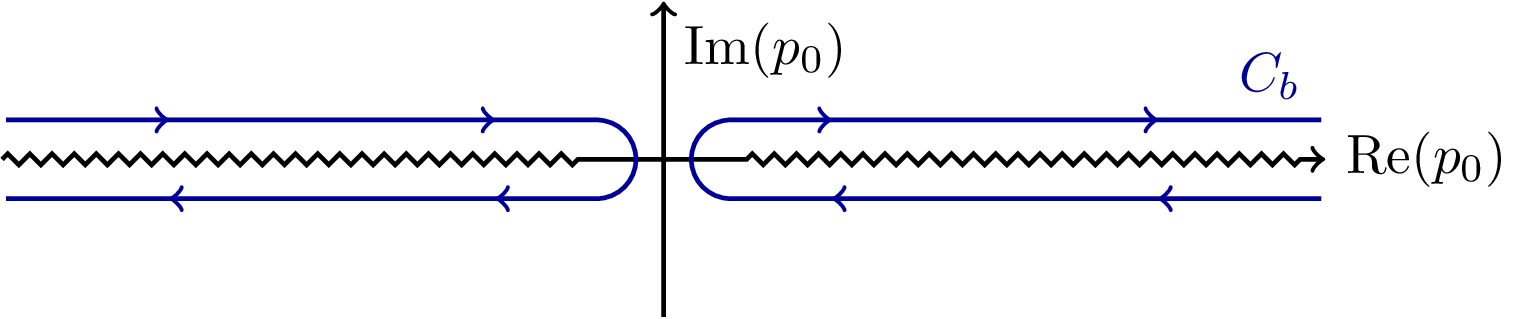
This is a really nice figure! Thanks a lot to the author!!
However, when compiling it, I receive the following warning:
Missing character: There is no 0 in font nullfont!
Missing character: There is no , in font nullfont!
I figured out that it is caused by line 222 which reads
\draw[->,black,thick] (0,\ymin,0,0) — (0,\ymax+0.02,0) node[above] {Im};
I think the problem is that the first 3D coordinate has four(!) arguments.
I changed it to the following and the warning disappears.
\draw[->,black,thick] (0,\ymin,0) — (0,\ymax+0.02,0) node[above] {Im};
Thanks, Jens! I fixed it now.