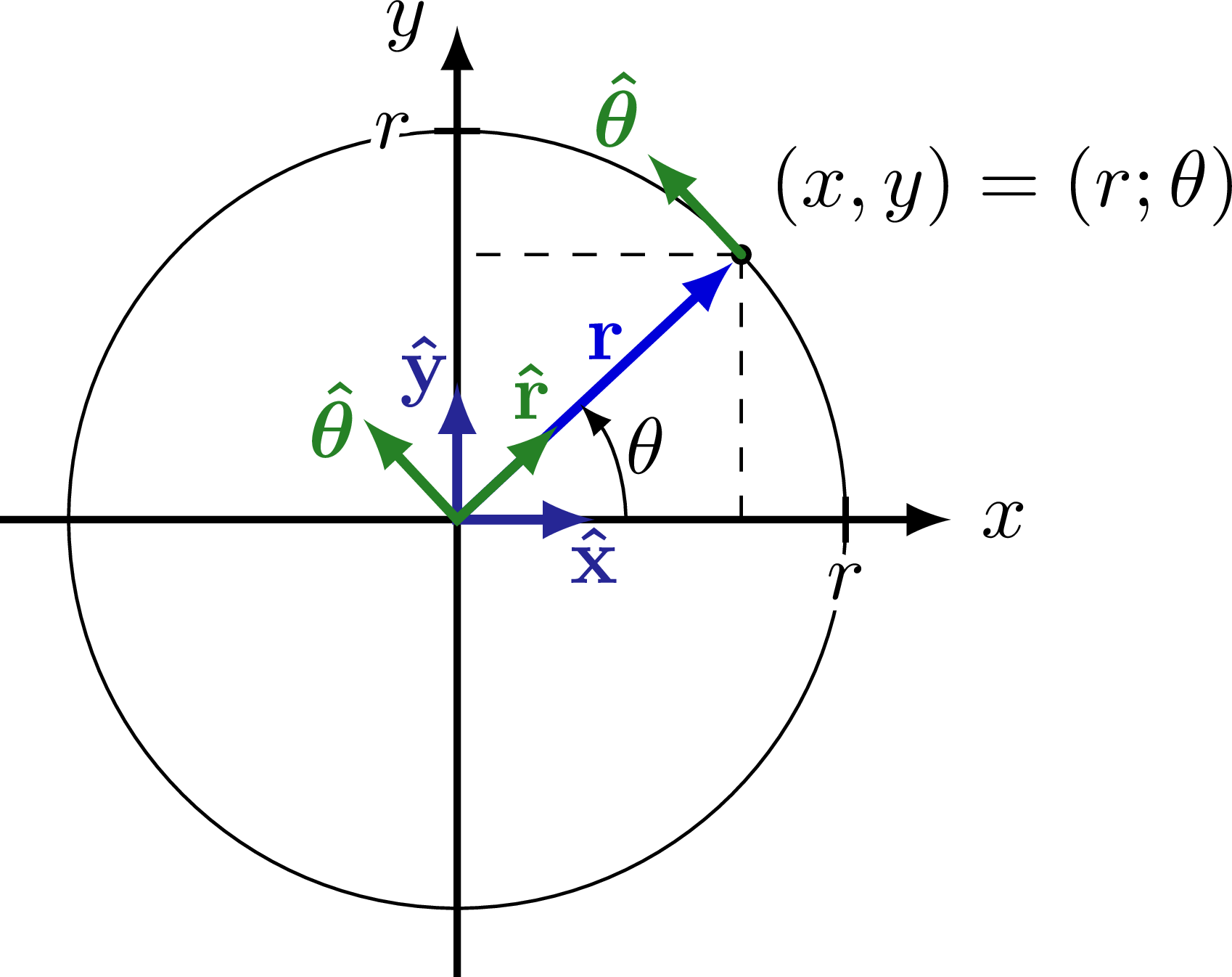
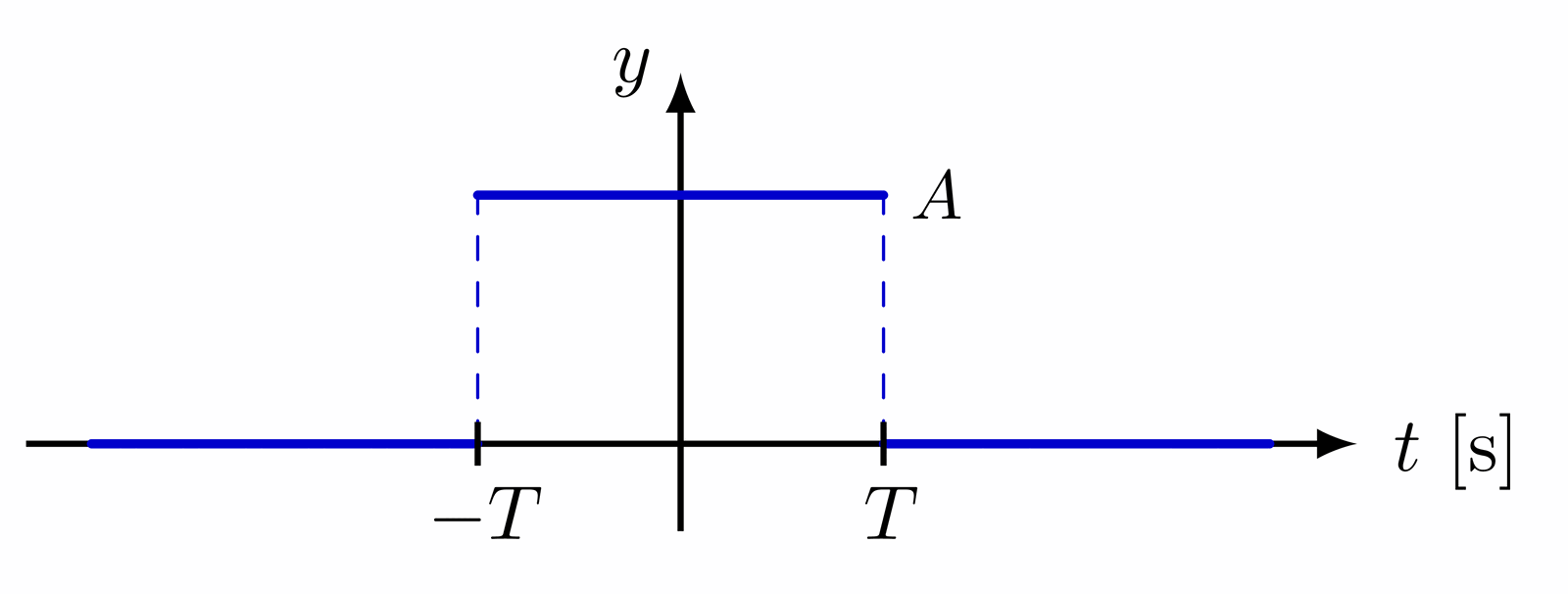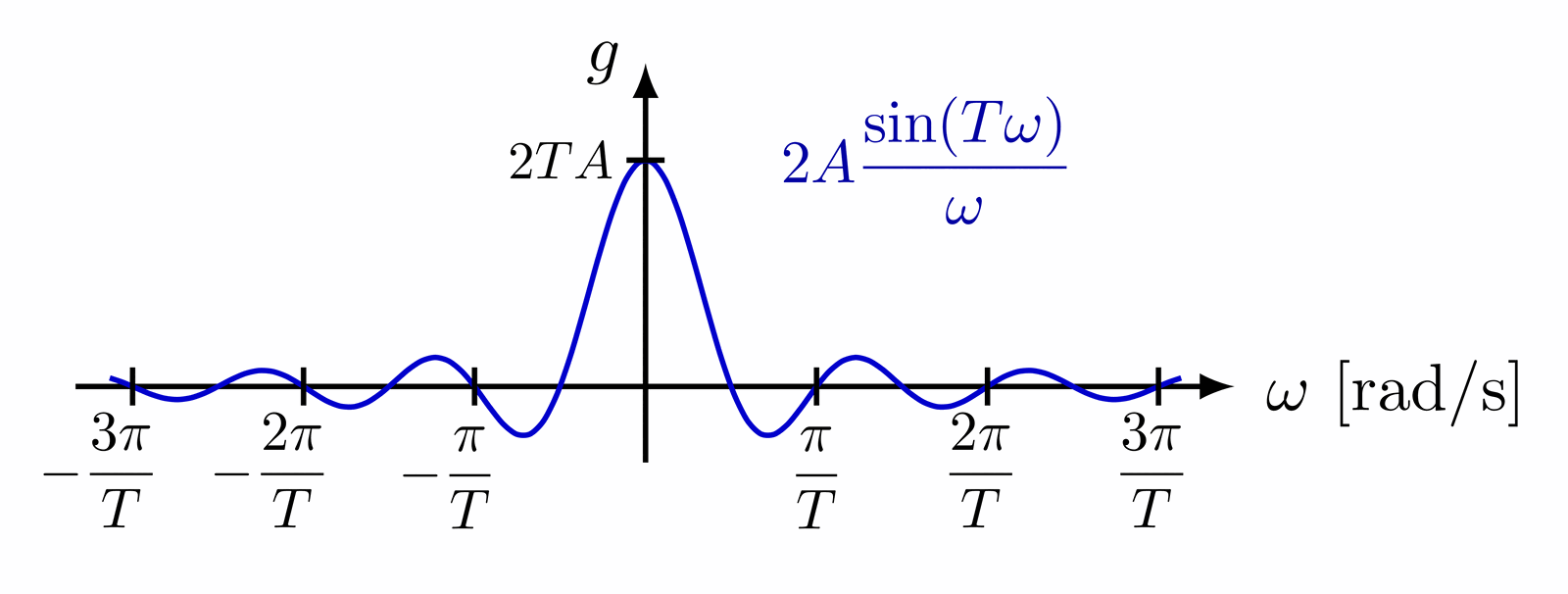
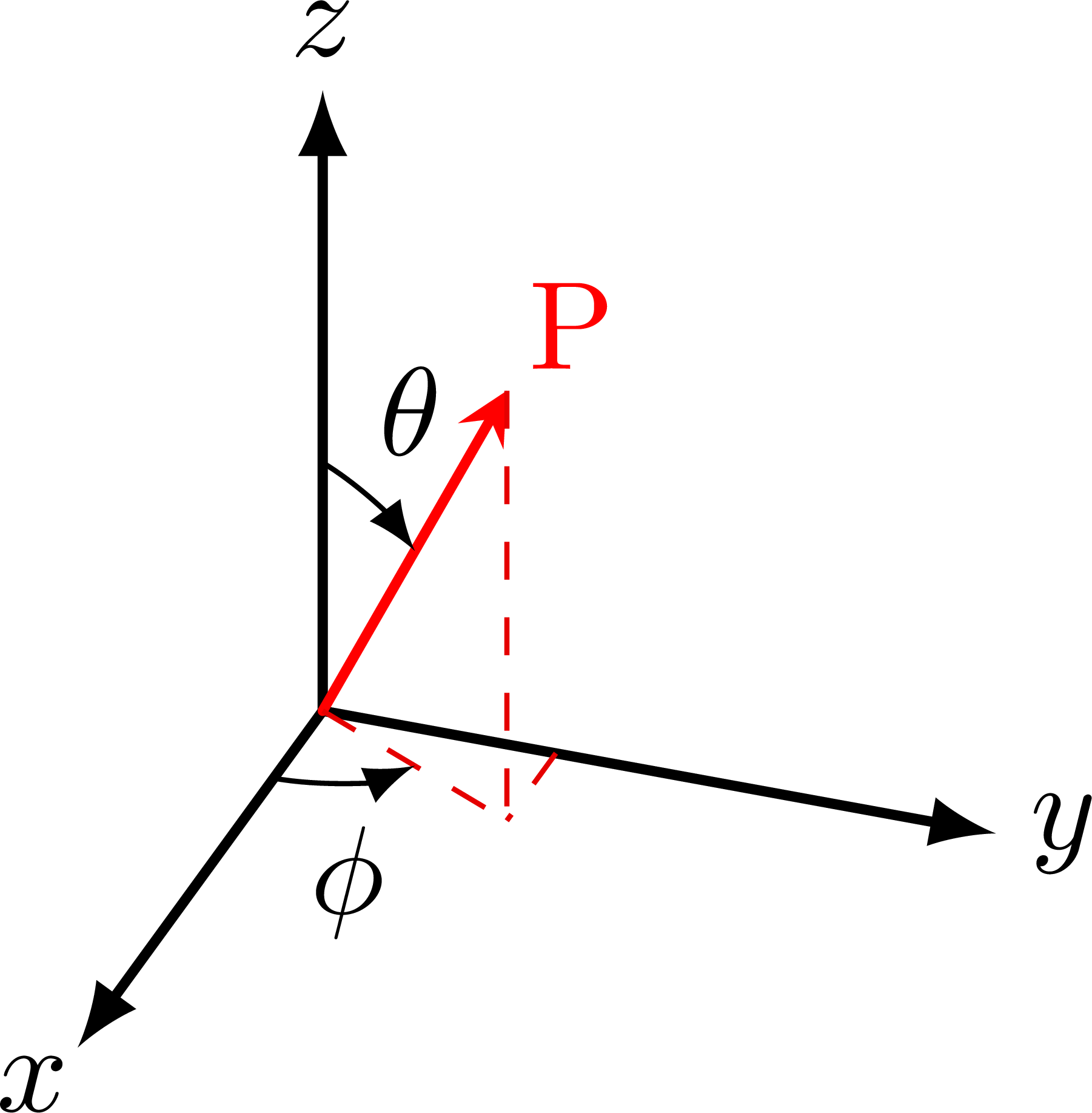
Complex plane with the imaginary and real axis, complex conjugation, polar coordinates, Euler’s formula, phasor, analytic representation of harmonic oscillators (helix), and rotation of a complex number in the complex or 2D real plane (comparing SO(2) and U(1)). Also have a look at the rotation matrix.
Edit and compile if you like:
% Author: Izaak Neutelings (January 2021)\documentclass[border=3pt,tikz]{standalone}\usepackage{amsmath}\usepackage{tikz}\usepackage{physics}\usepackage[outline]{contour} % glow around text%\usetikzlibrary{intersections}%\usetikzlibrary{decorations.markings}\usetikzlibrary{angles,quotes} % for pic\usetikzlibrary{bending} % for arrow head angle\contourlength{1.0pt}\usetikzlibrary{3d}\tikzset{>=latex} % for LaTeX arrow head\usepackage{xcolor}\colorlet{myblue}{blue!65!black}\colorlet{mydarkblue}{blue!50!black}\colorlet{myred}{red!65!black}\colorlet{mydarkred}{red!40!black}\colorlet{veccol}{green!70!black}\colorlet{vcol}{green!70!black}\colorlet{xcol}{blue!85!black}%\colorlet{projcol}{xcol!60}%\colorlet{unitcol}{xcol!60!black!85}%\colorlet{myred}{red!90!black}%\colorlet{mypurple}{blue!50!red!80!black!80}\tikzstyle{vector}=[->,very thick,xcol,line cap=round]\tikzstyle{xline}=[myblue,very thick]\tikzstyle{yzp}=[canvas is zy plane at x=0]\tikzstyle{xzp}=[canvas is xz plane at y=0]\tikzstyle{xyp}=[canvas is xy plane at z=0]\def\tick#1#2{\draw[thick] (#1) ++ (#2:0.12) --++ (#2-180:0.24)}\def\N{100}\begin{document}% COMPLEX\begin{tikzpicture}\def\xmax{2.0}
Click to download: complex.tex • complex.pdf
Open in Overleaf: complex.tex


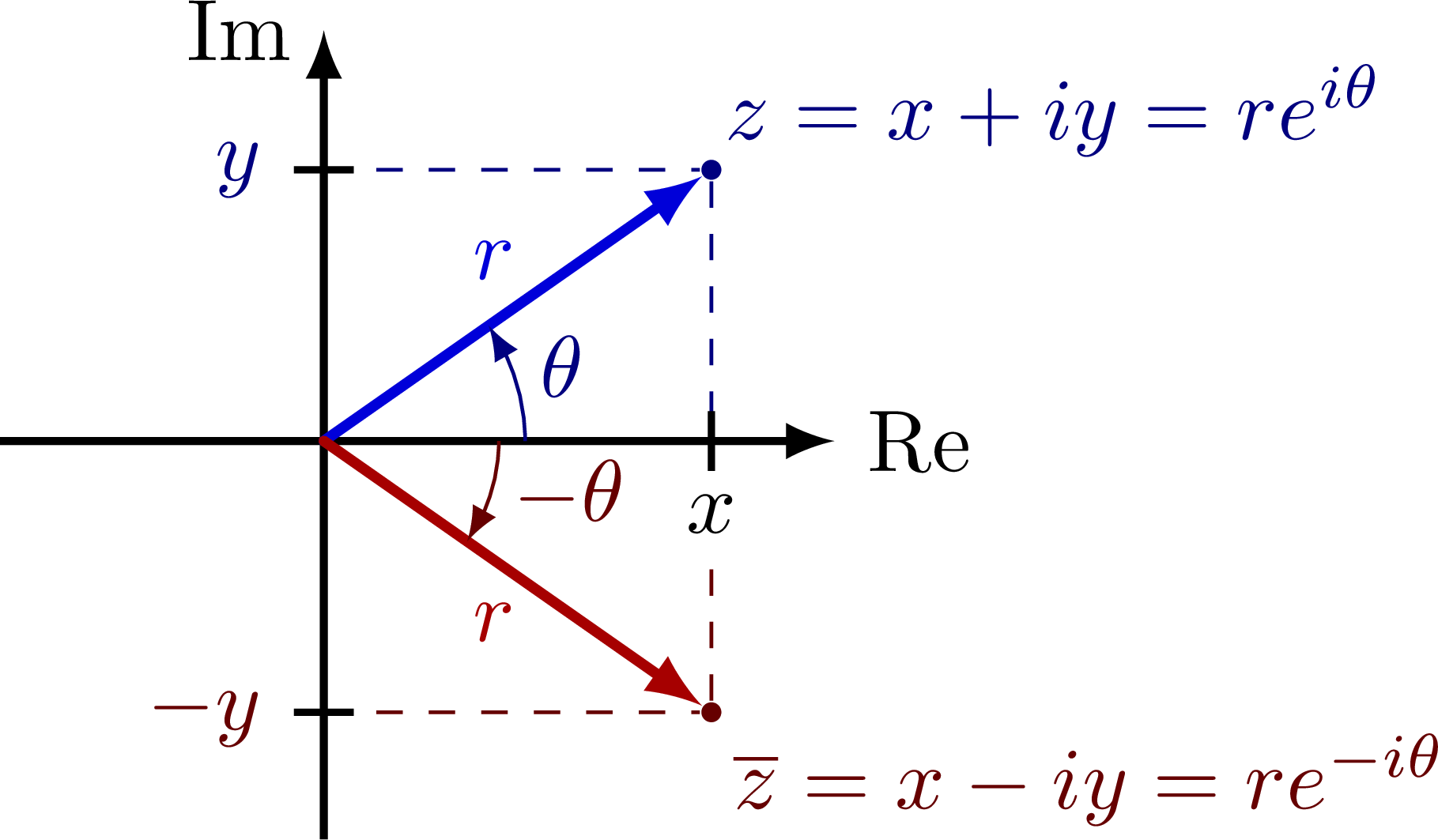
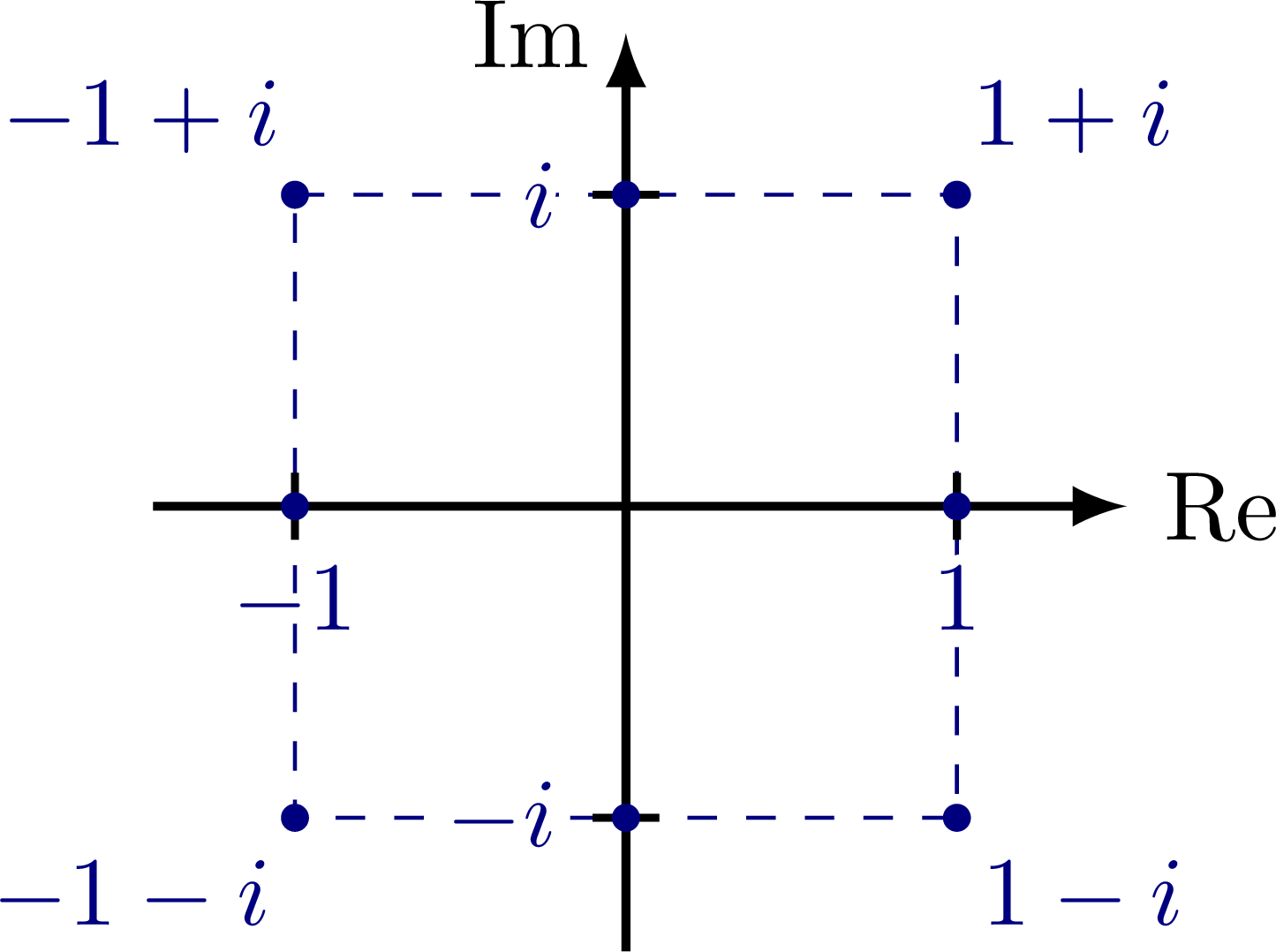
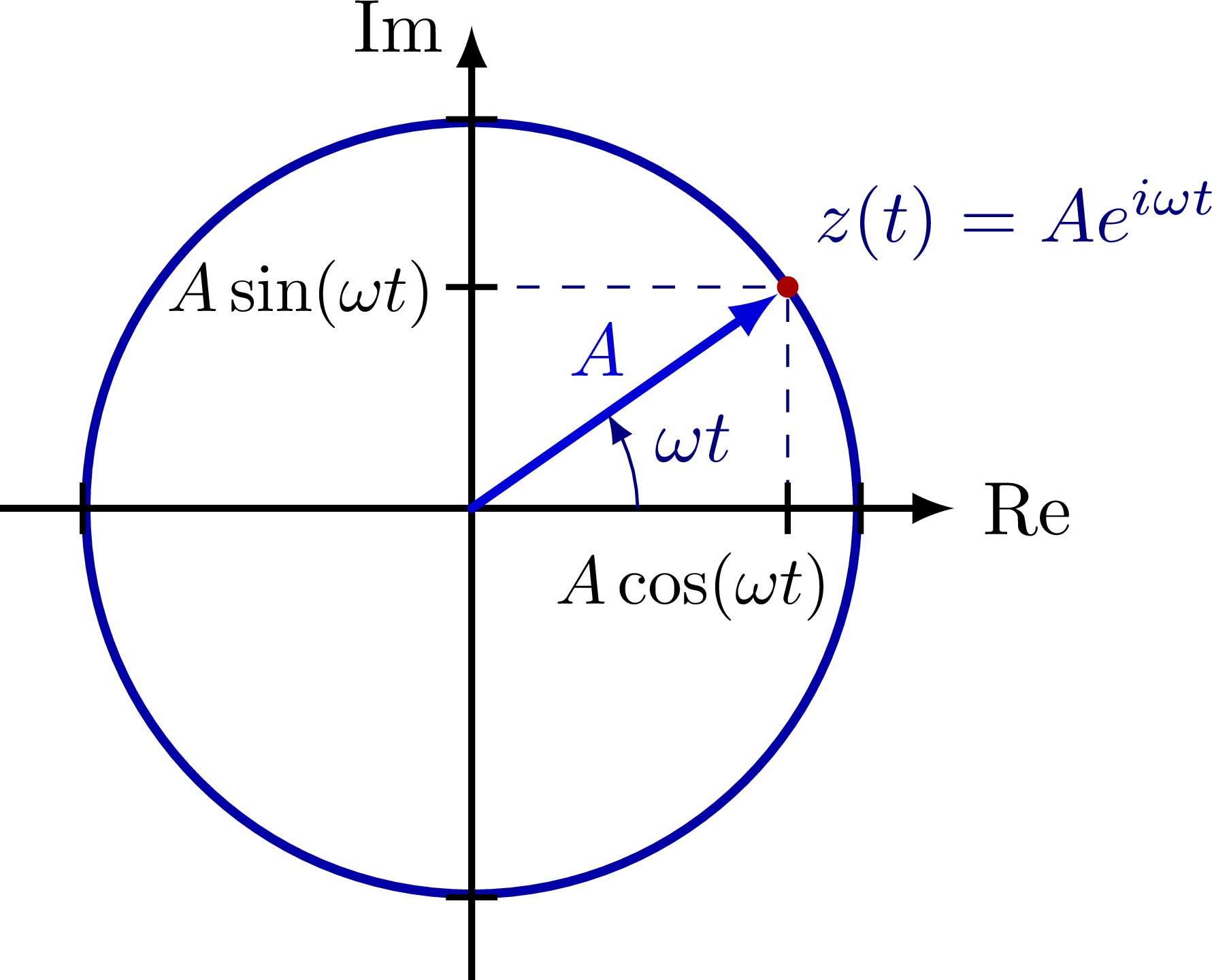
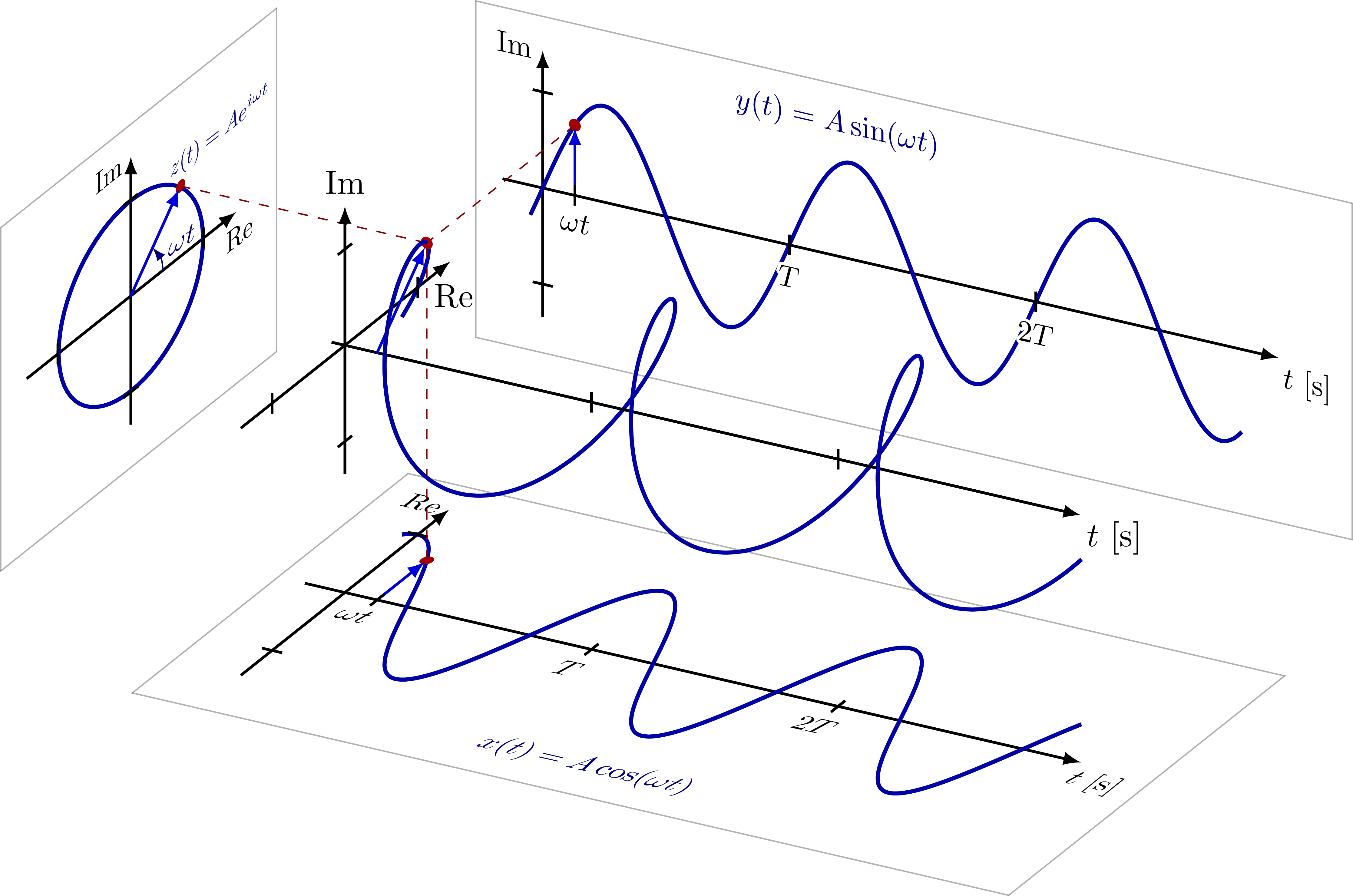

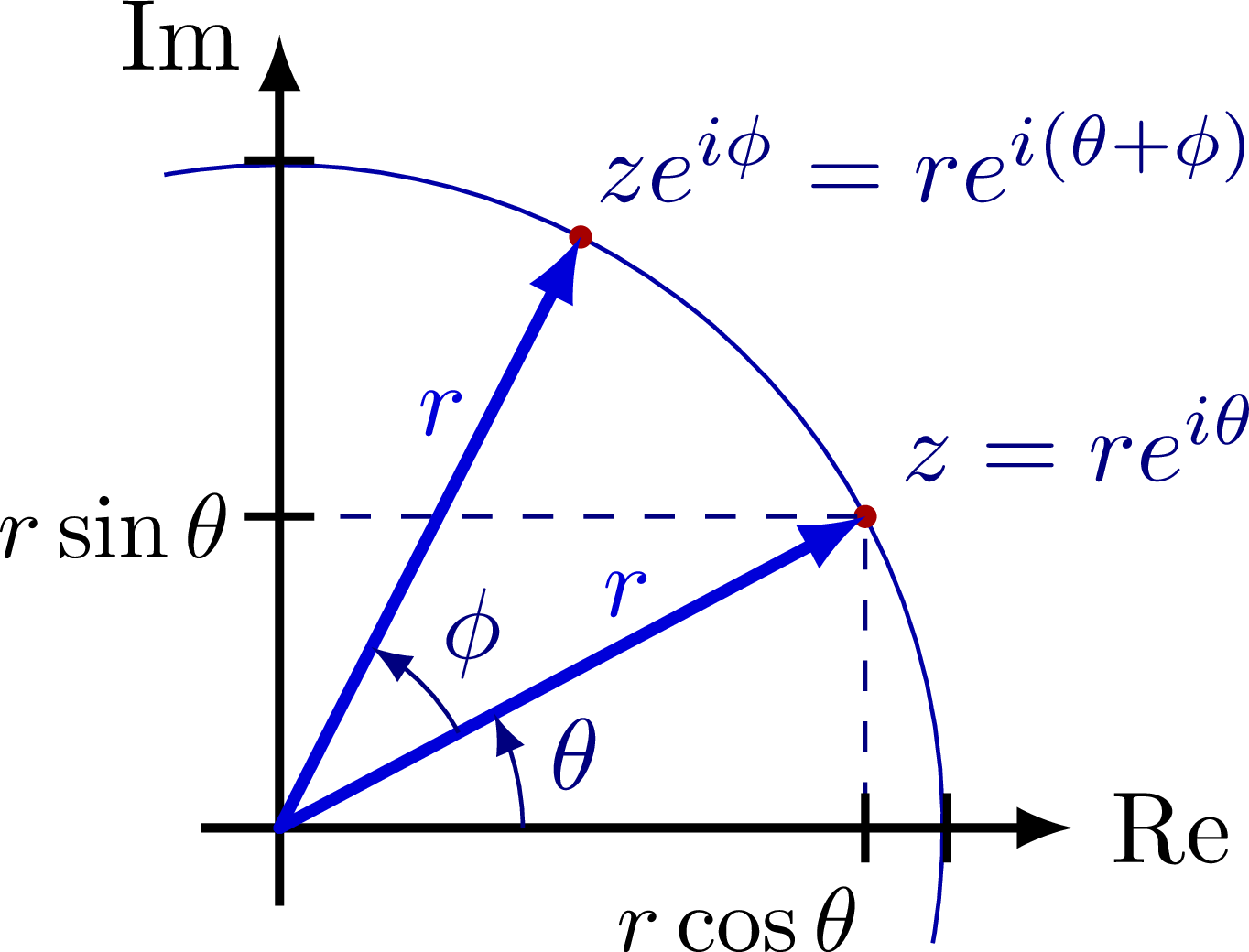

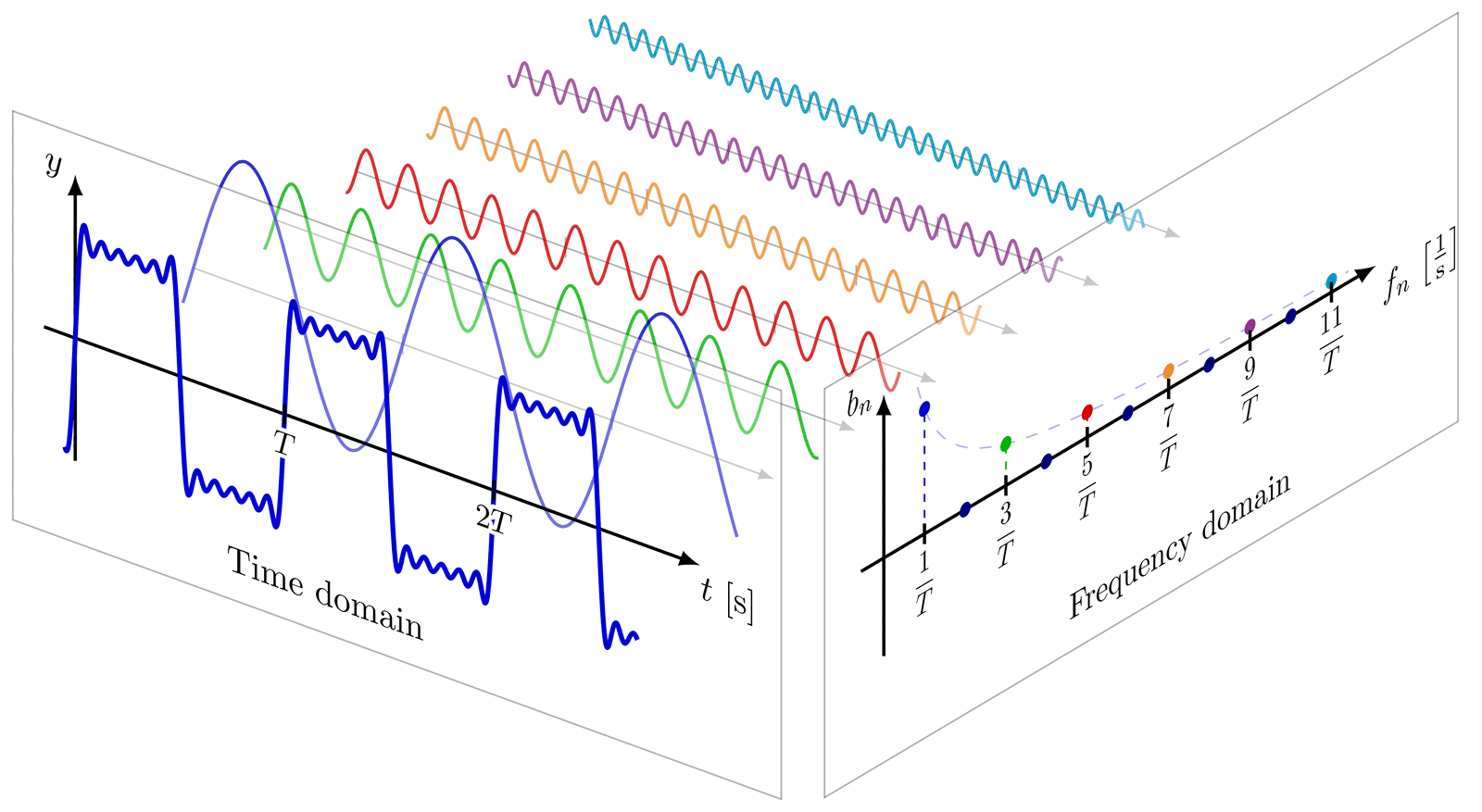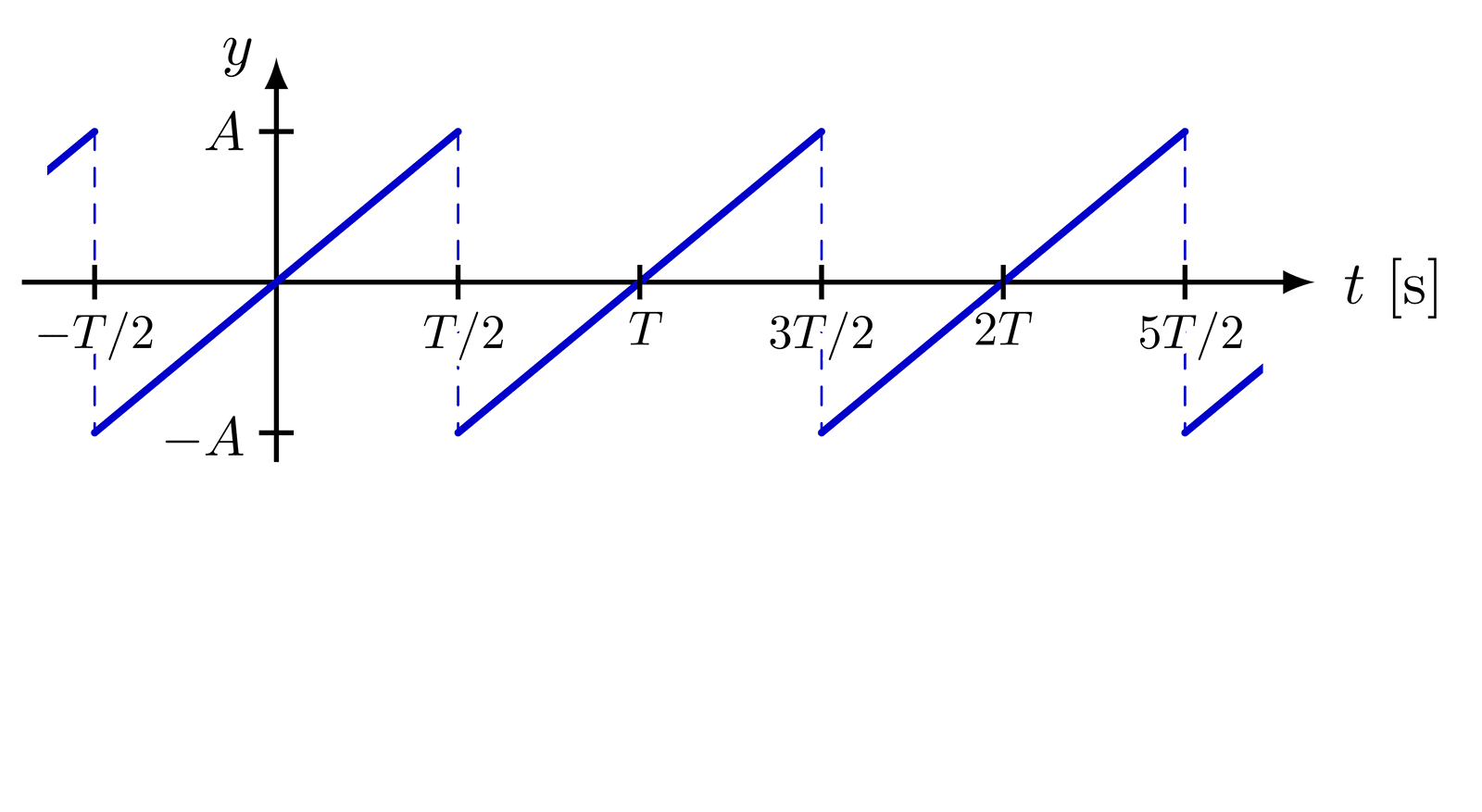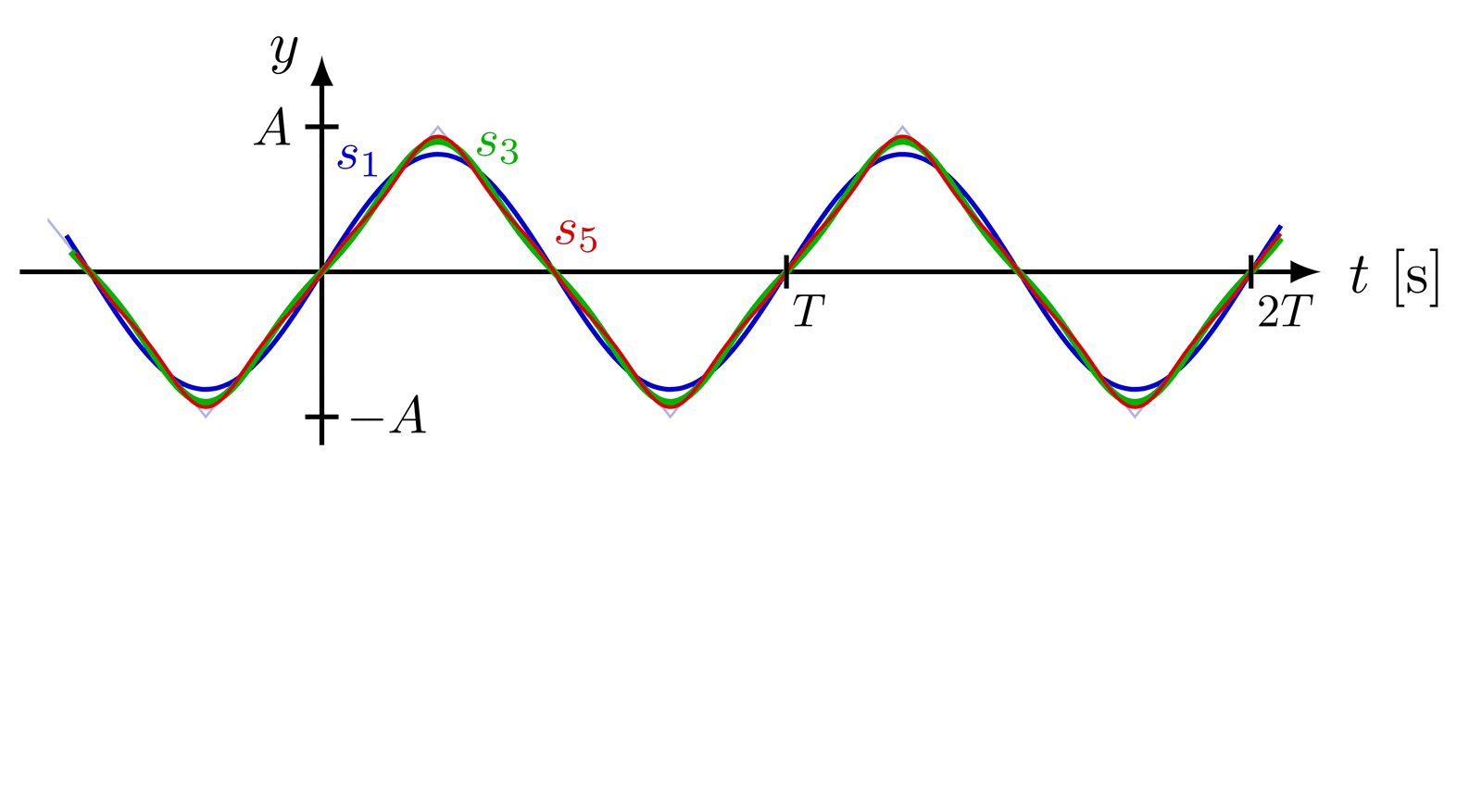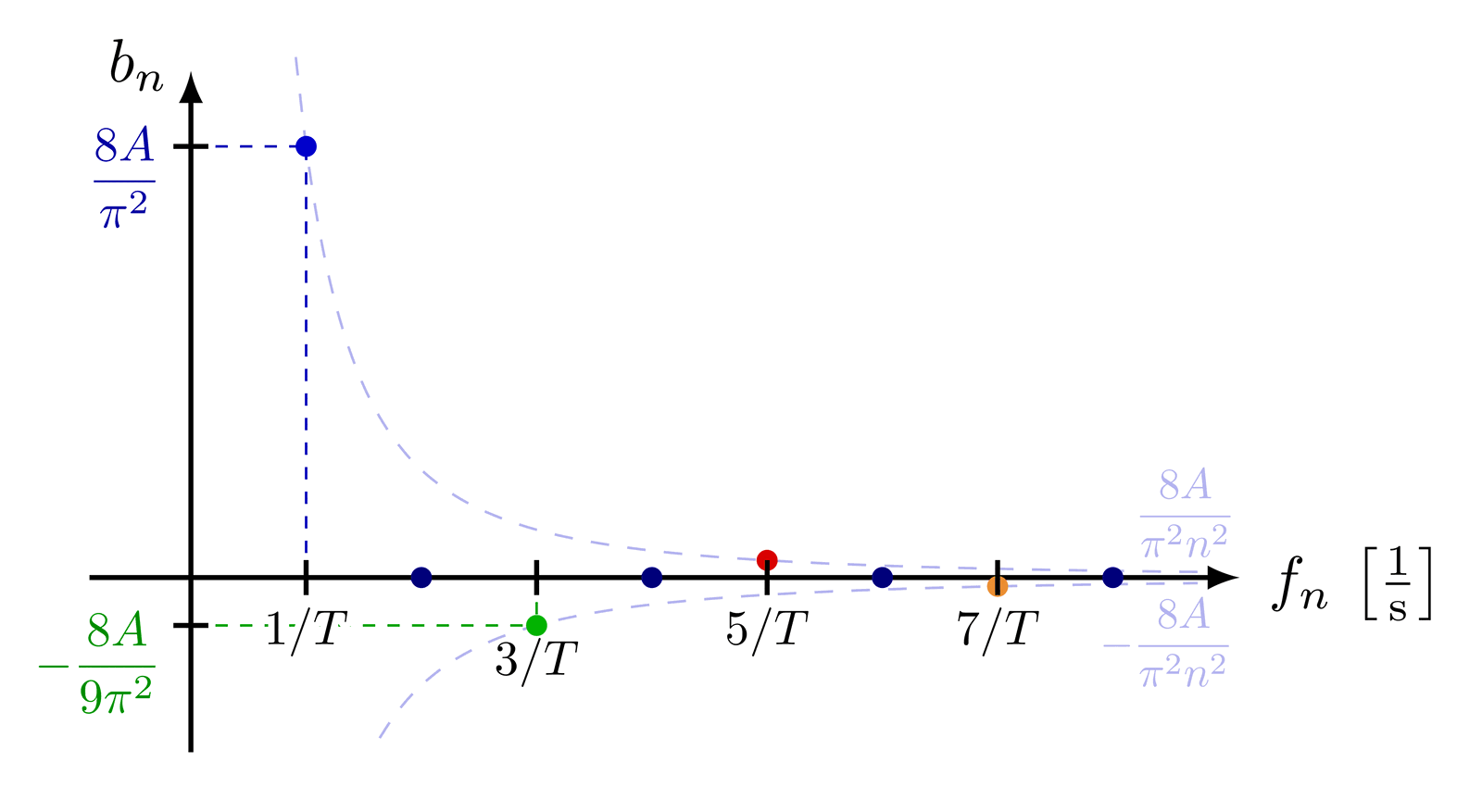
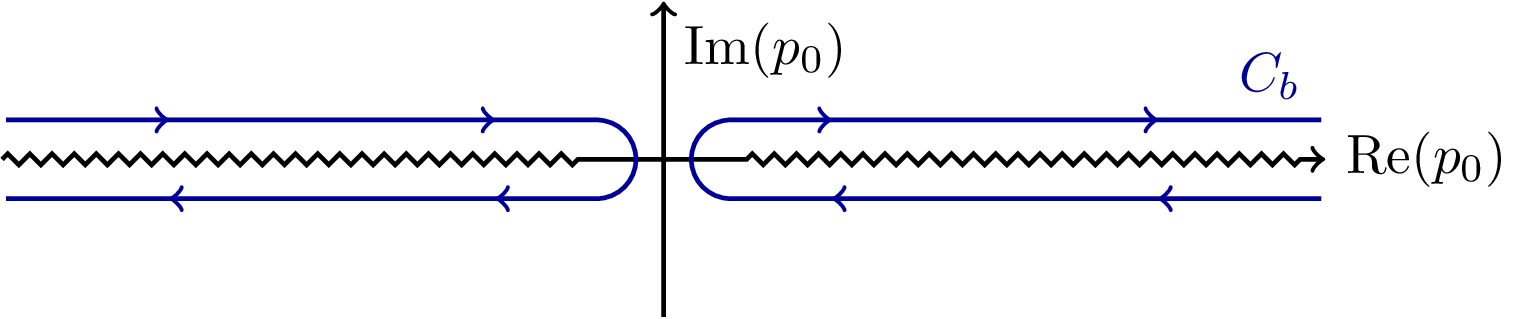
This is a really nice figure! Thanks a lot to the author!!
However, when compiling it, I receive the following warning:
Missing character: There is no 0 in font nullfont!
Missing character: There is no , in font nullfont!
I figured out that it is caused by line 222 which reads
\draw[->,black,thick] (0,\ymin,0,0) — (0,\ymax+0.02,0) node[above] {Im};
I think the problem is that the first 3D coordinate has four(!) arguments.
I changed it to the following and the warning disappears.
\draw[->,black,thick] (0,\ymin,0) — (0,\ymax+0.02,0) node[above] {Im};
Thanks, Jens! I fixed it now.